跨断层深海隧道衬砌变形规律及加固措施研究

王 淑 娟

(中铁十八局集团第四工程有限公司, 天津 300220)

随着“交通强国”战略的实施，国家对于地区公路、隧道的建设大力支持[1-3]。为了保障我国的海洋利益，我国修建了一大批跨海工程，例如我国正在建设的海底隧道工程有深圳妈湾港海底隧道、汕头海湾、大连湾海底隧道等，其中正在建设的胶州湾第二隧道将成为目前为止世界最大规模的海底隧道[4-8]。这些跨海隧道的建设将促进我国在能源、交通、军事领域的发展。而跨海隧道的建设经常遇到断层破碎带，这些断层破碎带在地震等荷载作用下容易造成隧道发生不均沉降和剪切破坏，如在集集地震 (1999年)、汶川地震 (2008年)和熊本地震 (2016年)中，由地震引起的断层错动导致大量隧道产生裂纹甚至坍塌[9-12]。

断层破碎带形成的原因主要是断层内土层强度低、松散性高，在周围地层的挤压下极易发生岩石破碎[13-17]。因此研究高水压条件下隧道穿越断层破碎带的围岩变形、衬砌应力位移变化等一系列问题对于深海隧道工程的建设具有重要的意义。

国内外科研人员针对隧道穿越断层破碎带及断层错动作用下隧道衬砌结构的影响做了大量的研究。陈兴强[18]研究了川藏铁路穿越断层破碎带时隧道最大埋深处的最大水平应力；周光新等[19]分析了跨断层隧道的破坏机制，研究了衬砌厚度、节段长度、隧道断面形式等因素对隧道抗剪切性能的影响；Yang 等[20]地下矿山岩体及结构面的力学性质对于巷道稳定性的影响；李瀚源等[21]建立了隧道纵向等效连续化模型，分析了跨断层隧道结构的力学响应与隐伏断层错动的关系；罗金涛等[22]研究了走滑断层错动下隧道衬砌结构的力学响应，分析参数包括节段长度和变形缝宽度；颉永斌等[23]基于筒仓理论，建立了跨断层隧道纵向荷载的理论计算模型，通过室内模型试验和数值模拟分析了隧道埋深、断层宽度等参数的影响；Zhang等[24]以2016年的熊本地震为例，分析了地震参数、构造形态等因素造成隧道损伤的原因并提出了相关的修复准则；郑书笛等[25]采用MIDAS/GTS NX分析了超前小导管及其注浆对隧道穿越断层时的支护效果；黄健陵等[26]利用社会网络分析法(SNA)分析了穿越断层的破碎带的高风险因素；唐浪洲等[27]分析了走滑断层错动下隧道的位移、应力和应变响应。丁祖德等[28]分析了断层错动下隧道ECC衬砌和混凝土RC衬砌的抗错动能力；赵旭等[29]利用ABAQUS建立了断层错动下隧道衬砌响应的数值模型，分析了逆冲断层错动、走滑断层错动以及倾向滑移断层错动下隧道的内力位移变化；张超翔等[30]分析了双断层错动下隧道的位移及剪应力响应规律，集合混凝土应力-应变准则建立了双断层共同作用下的三维数值模型；龚林金等[31]依托水阳高速胜利隧道分析了隧道穿越不同倾角的断层时围岩的变形规律；李杨杨等[32]为了研究跨断层隧道开挖扰动下围岩裂隙涌水机制研制了非亲水性流固耦合相似材料，并开展了流固耦合条件下隧道突涌水的模拟试验；梁建文等[33]采用CDP模型建立了三维壳-弹簧的力学模型，分析了断层错动下盾构隧道的结构力学响应；Erami等[34]考虑了管道-土壤之间的相互作用，分析了管道在反向断层作用下的力学响应。

断层错动下隧道衬砌的力学及位移响应已有大量研究和成果，但在高水压作用下隧道穿越断层破碎带的围岩稳定性和衬砌的安全性研究很少。因此，本文依托某下穿海域地铁隧道，通过数值模拟分析了高水压作用下跨海隧道穿越断层破碎带的稳定性及加固措施。

1 工程实例分析

1.1 工程概况

如图1所示，该段研究区域隧道穿越一段断裂带，该断裂带由强风化裂隙岩组成，断裂带长37 m，宽9 m，倾角72°。该海域水深约12 m，左右线隧道长度为172.8 m和206.2 m。该区段的隧道施工采用土压泥水盾构，隧道支护采用内径5.5 m、外径6.2 m的预制混凝土衬砌。隧道埋深10 m，线路最小曲率半径300 m，最大坡度29%。

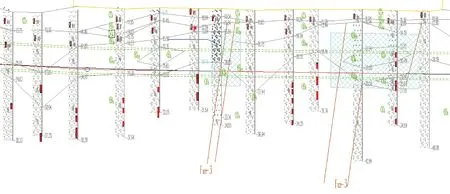
图1 隧道穿越断层破碎带横截面图

1.2 计算模型建立

本研究采用ABAQUS有限元数值模拟软件建立三维数值模型。如图2所示，隧道的外径为6.2 m，内径5.5 m，考虑到模型尺寸效应，根据Rodriguez[35]所做的模型尺寸试验，对于隧道开挖模型的深度应该大于H+4D，长度大于H+3D，宽度大于H，H为隧道中心线距地面深度，D为隧道直径。因此，最终选取三维模型的计算尺寸为94 m×66 m×45 m，二维模型的计算尺寸为66 m×45 m。在ABAQUS中采用八节点减缩积分单元C3D8R单元来模拟土层，八节点单元C3D8单元来模拟土压盾构、管片及注浆层，B31梁单元用来模拟水平及径向注浆管。模型网格采用单精度，在隧道关注位置采用更加细化的网格，其他区域采用粗略网格。

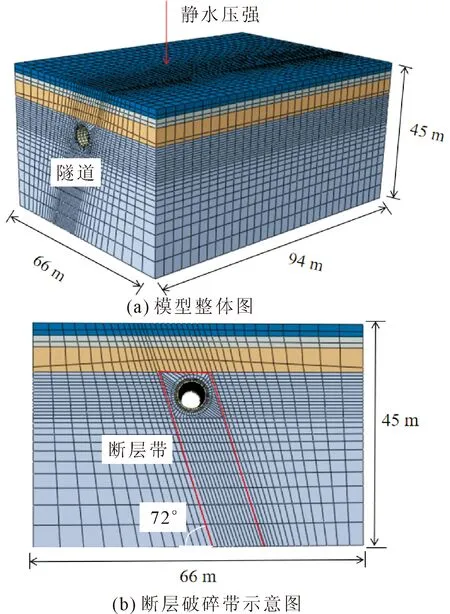
图2 数值模型图

模型边界采用齐次边界，即模型底部采用全约束，顶部为自由边界，四周约束法线方向。模型中的EPBS壳体，注浆层、土层、管片均采用绑定约束。同时在计算模型中采用了如下假定：(1)土体材料为均匀且无限远；(2)不考虑施工过程中管片拼接缝以及螺栓连接的影响，不考虑接缝之间的滑移；(3)忽略施工过程中的时间效应及机器等待时间的影响；(4)忽略地下水及动水压力的影响。

1.3 模型计算参数选取

数值模型中土层及破碎带采用摩尔-库仑本构模型，预加固措施及其他单元采用线弹性模型管棚及径向注浆，土层参数如表1所示，其他参数如表2所示。通过现场的监测资料，土压盾构的平均注浆压力为0.2 MPa，掌子面的顶推力为1.732 MPa，考虑时效硬化的注浆层的参数如表1所示。如图3所示，管棚法中采用在隧道拱顶180°范围内进行注浆，管道参数如表3所示。径向注浆的有效加固范围如公式(1)所示：

(1)

式中:D为加固区的范围；R为浆液扩散半径；S为管道间距。

表1 岩土计算参数

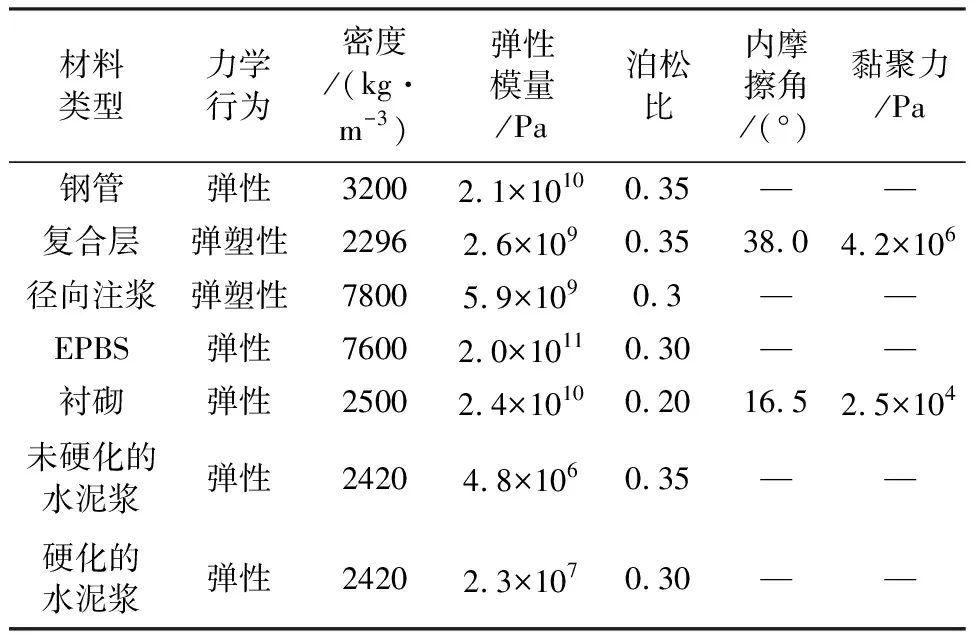
表2 预加固措施的模拟参数

表3 管棚法模拟参数

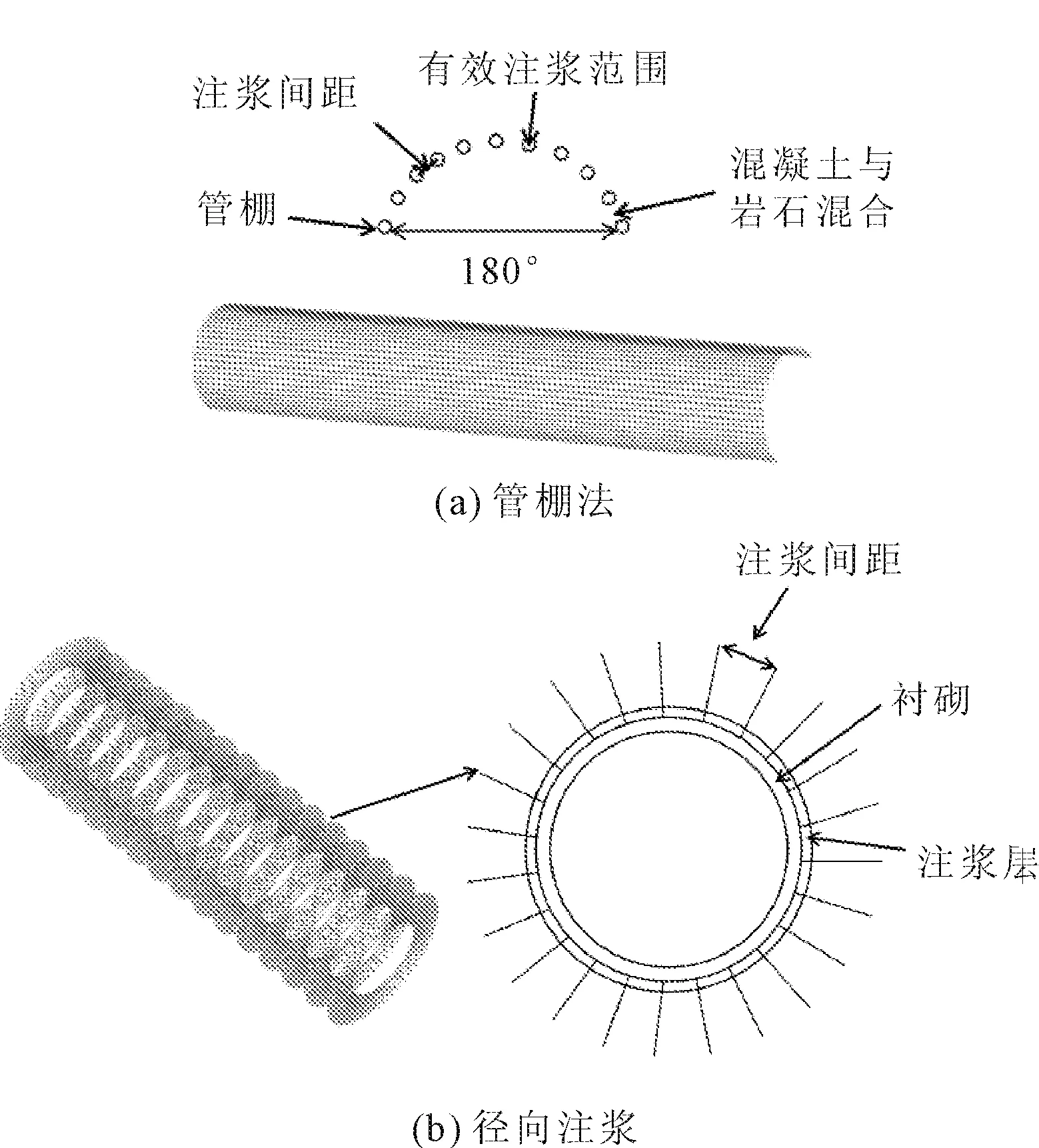
图3 隧道穿越断层破碎带的加固措施

1.4 隧道施工模拟方法

(1) 隧道施工前的地应力平衡。考虑海水静水压强的作用，因此在模型表面施加静水压力，使土体在自重及高水压作用下达到平衡，使土体位移清零并达到开挖前的应力状态。

(2) 在ABAQUS中利用“生死单元”的方法模拟隧道土体的开挖、衬砌的安装以及注浆管的安装。在隧道开挖过程中，注浆压力、顶推力、注浆时效硬化、开挖围岩的应力释放等均在相应的分析步激活或杀死。

(3)管棚法或径向注浆法均在隧道未穿越断层破碎带前进行施工，因此隧道需要进行停机操作。

2 隧道稳定性的判断方法

隧道的稳定性一般用围岩的位移、衬砌的应力变化等方面进行分析。如图所4示，Sakurai[36-37]通过大量的试验分析了隧道施工时临界应力应变的关系，将开挖围岩的单轴抗压强度和弹性模量结合起来进行了分析，得到了3个危险等级来评价隧道的稳定性，三种不同等级的评价如表4所示。三种隧道围岩等级的计算公式如下所示：

(2)

Uc=r·εc

(3)

式中:E为杨氏模量；σc为单轴抗压强度；εc为临界应变；r为隧道半径；Uc是临界位移。

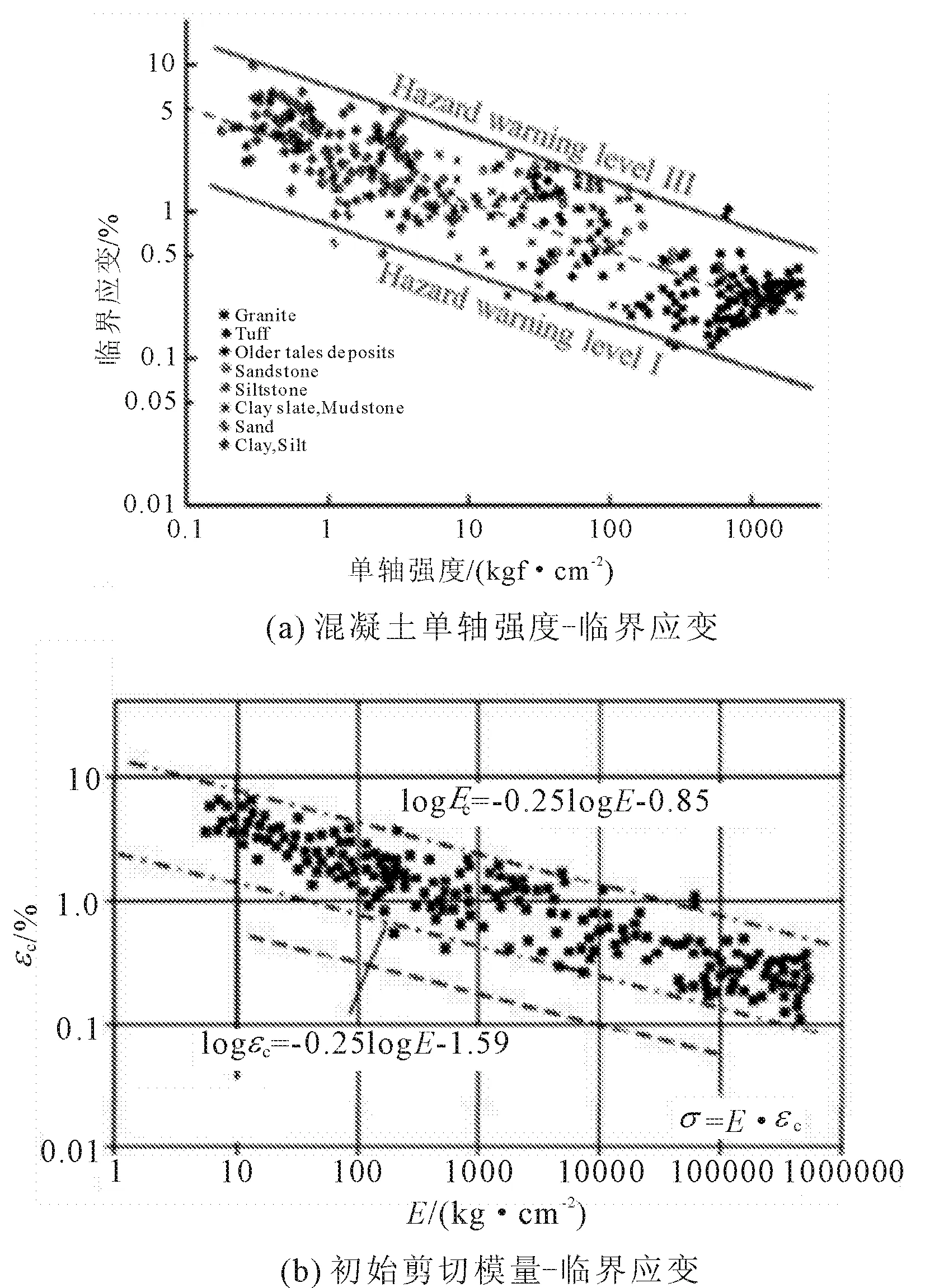
图4 隧道稳定性判定图[34-35]

表4 危险等级(HWLs)

式中:Ei是杨氏模量,εc为临界应变。

3 模型可靠性验证

对于本文中的模型的可靠性验证采用解析解的方法。隧道支护系统的解析解由Einstein等[38]通过大量的现场试验得到，但这种方法假设围岩为各向同性的均匀体且不考虑隧道停机等时间因素，一般将这种方法应用到圆形隧道中，对于马蹄形隧道的准确性很低。相关计算公式如下：

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

断层内的隧道轴力和弯矩是主要关注点，因此选取断层内某段隧道进行弯矩和轴力的监测。在上述解析解中，假设断层内的水平应变和垂直应力是统一的，在计算中垂直应力同样要考虑静水压强的影响，因此垂直应力需要加上海水压力。如图5所示，衬砌环向角度的轴力和弯矩的数值解和解析解的趋势相同，误差也控制在20%以内。因此数值模型具有较好的可靠性。

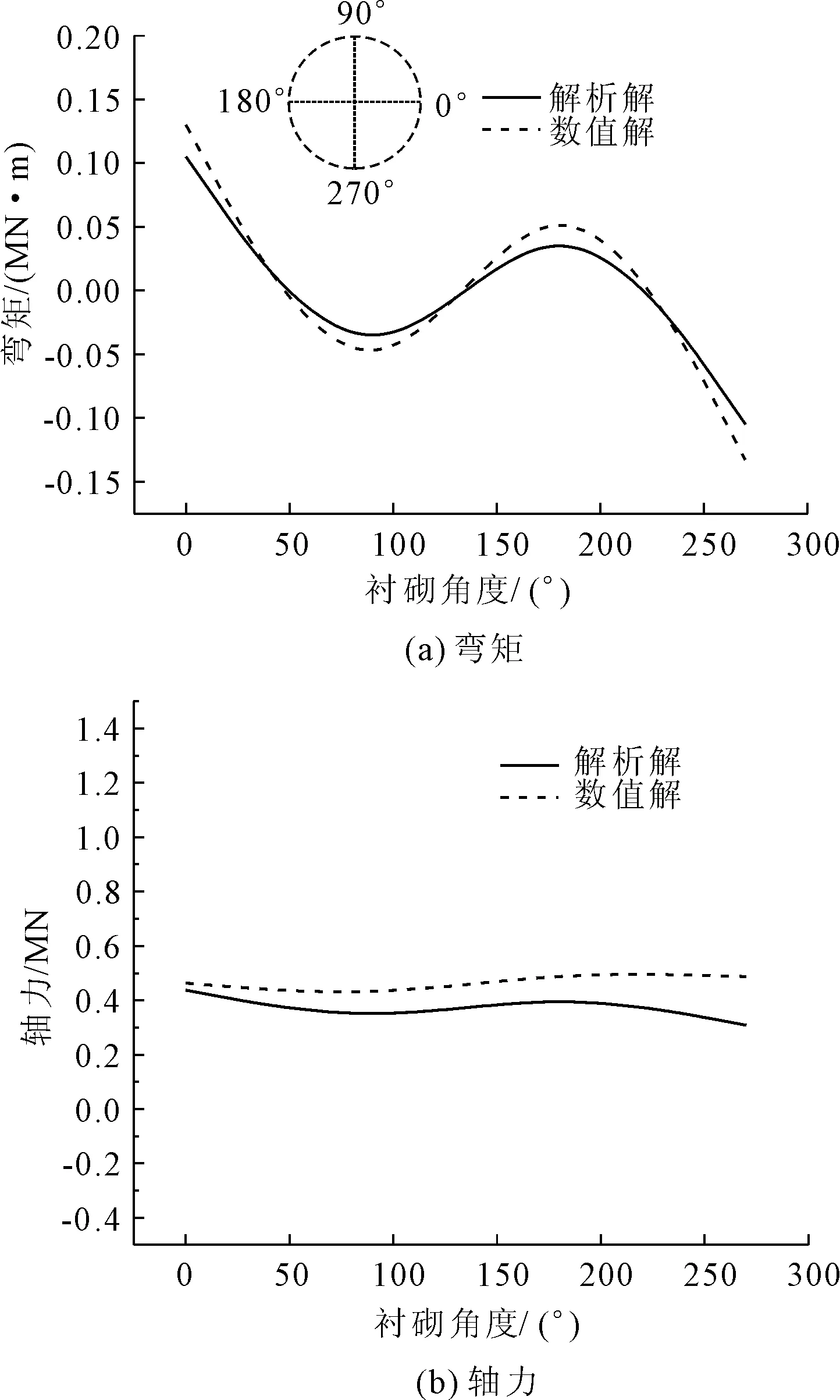
图5 衬砌弯矩和轴力图

4 计算结果分析

4.1 未加固下隧道稳定性分析

如图6 所示为隧道穿越断层后土层沉降与塑性区分布图。从土体的塑性应变来看，在进入断层和退出断层两段的土体的塑性区发生了明显屈服，塑性屈服区沿着断层面向下延伸，这将造成相邻衬砌的错移，造成衬砌发生剪切破坏，这也是导致隧道衬砌发生渗漏水的原因。由周围土壤的沉降观察到，在未进入断层前，隧道为底部隆起而顶部沉降，当进入断层破碎带后，隧道为左上方隆起而右下方沉降，这是因为隧道开挖到断层带后，周围的土层达到稳定，在应力释放后发生了较大变形。如表5所示，通过与Sakurai的方法进行比较，跨断层隧道的临界应变和临界应力均超过了限值，这表明隧道已经处于不稳定状态。

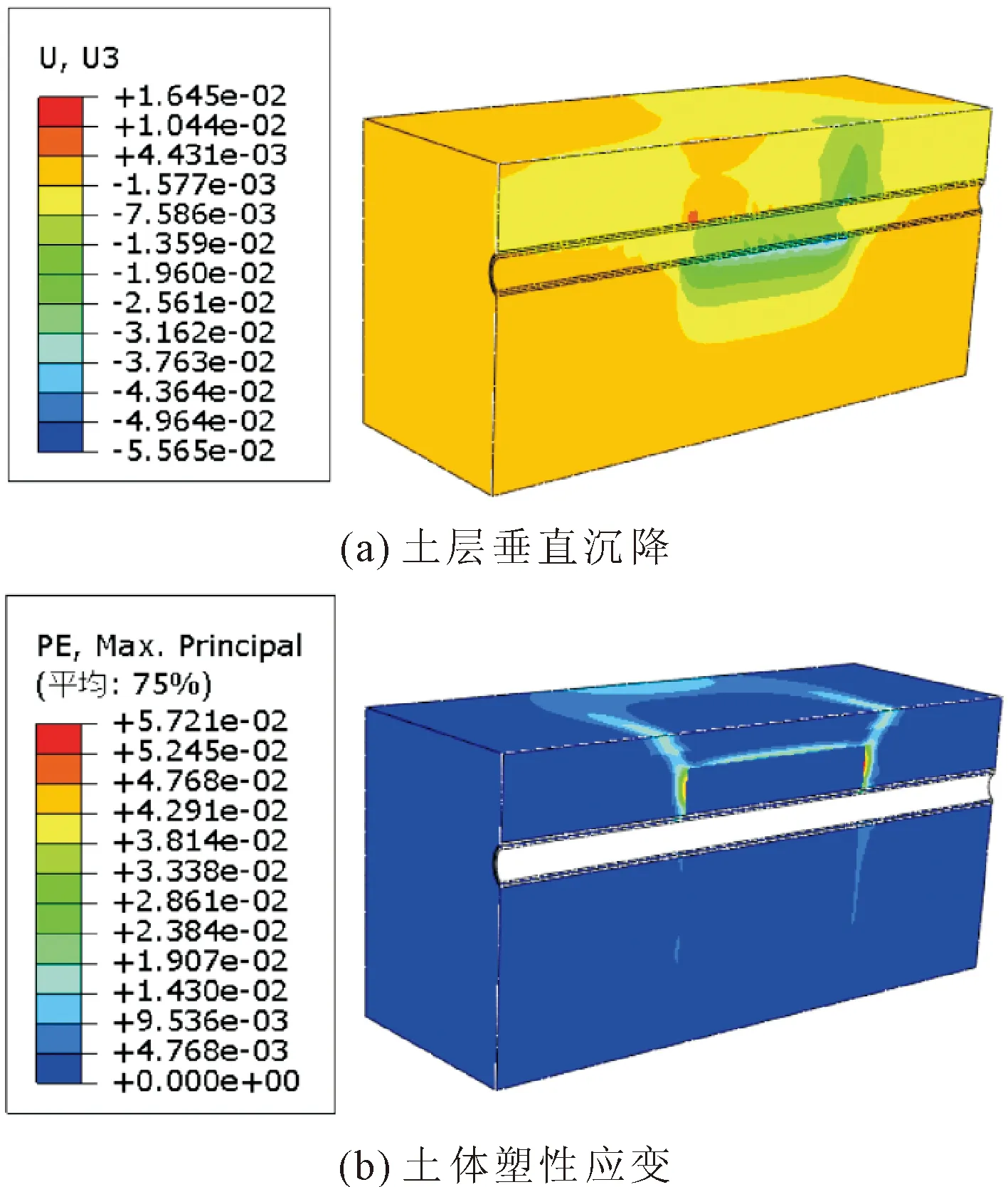
图6 隧道穿越断层后土层沉降与塑性区分布图

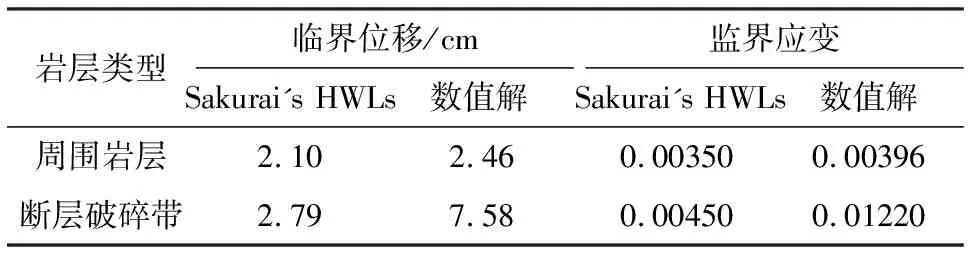
表5 隧道稳定性判定

如图7所示为隧道监测环数与位移应力横截面监测点。分别监测隧道进入断层前的5环与在断层内的两环。如图8—图10所示，监测截面的最大变形、竖直沉降和最大主应力分别被监测。随着隧道施工接近断层破碎带，衬砌的位移和应力都在不断增加，当第12环衬砌施工完毕后，最大变形量相较于前一环衬砌最大变形由7.9 mm增加到11.1 mm，增加幅度达到40.6%。最大沉降量为10.1 mm，衬砌表现为顶部受压而底部受拉，其中左边拱顶和右边拱底产生应力集中现象，这与断层的倾角高度相关，最大压应力达到5.2 MPa。断层内的隧道衬砌第15环和第16环的最大变形为16.2 mm。因此隧道施工过程中，进入和退出断层段的衬砌更为危险，在该部分的衬砌极易由于断层的错动而发生剪切破坏，导致隧道的渗漏水。

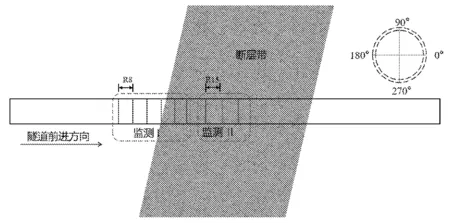
图7 隧道监测断面示意图

图8 隧道穿越断层前后的最大变形图

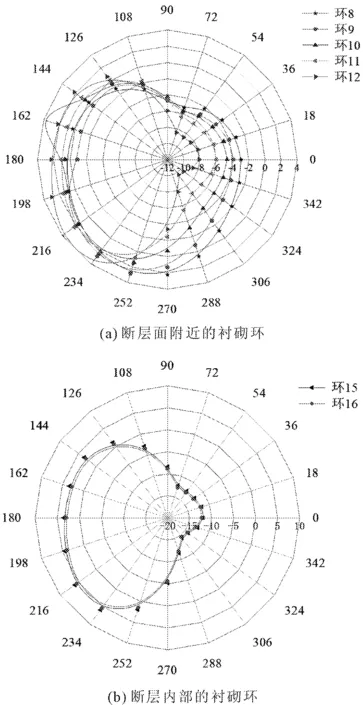
图9 隧道穿越断层前后的竖向沉降图

图10 隧道穿越断层前后的最大主应力图

4.2 管棚法和径向注浆法加固效果分析

如图11、图12所示为隧道经过管棚法加固后的地表沉降云图和塑性区分布图。地层的最大沉降位置为断层破碎带的上方，最大变形为18.7 mm，相较于未加固而言，地面的最大沉降量减小了67.27%，管棚法加固效果显著。土层的塑性区依然非常明显，主要存在于断层与周围土层的接触面之间。如13图所示为管棚的竖向沉降和应力云图。最大沉降达到了15.5 mm，最大应力值为150.1 MPa。根据相关的研究，管棚内部的水泥浆液可以通过弹性模量折减的方法等同于一定面积的钢管，本次研究的注浆管直径60 mm，横截面面积为1 306 mm2，最大屈服应力为392 MPa，通过计算得到最大的轴力为512 kN，而数值模拟中的最大轴力为188 kN，由此可以看出，超前支护管并没有达到限值轴力，可以继续承担部分荷载。

图11 隧道施工完毕后周围土层沉降图

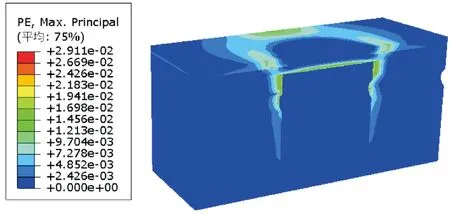
图12 隧道施工完毕后周围土层塑性区分布图

图13 管棚沉降和应力图

如图14、图15所示为经过预加固后的隧道应力和位移云图。隧道衬砌的最大应力为11.92 MPa，最大位移为11.5 mm。隧道的位移云图和应力云图均表明与断层破碎带的滑移方向相关，最大应力和变形发生在断层破碎带内。断层破碎带的滑移不仅会造成隧道坍塌和剪切，还有可能导致隧道的旋转，隧道旋转的评价采用以下公式：

(12)

式中:ω为旋转指数；θ为旋转角；uz1和uz2分别为隧道拱侧端的沉降量，也可利用拱底和拱顶的水平位移差值来表示；D为隧道直径。

图14 施加管棚法后隧道的应力和位移图

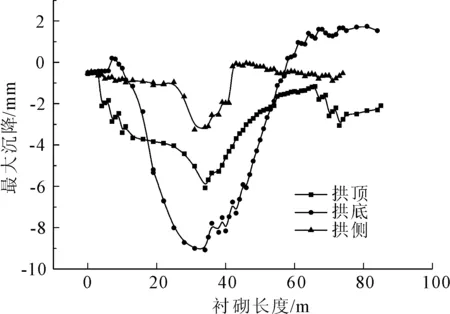
图15 隧道衬砌沉降图

通过对隧道拱顶、拱底和拱侧的监测，可以了解隧道的旋转倾向。隧道的最大沉降发生在拱顶，达到8.5 mm，拱底的沉降为6.2 mm，拱侧的沉降为2.6 mm，因此可以计算得到整段隧道的最大旋转指数为3.7×10-4。如图16所示为径向注浆管的最大变形和应力云图。径向注浆管的最大变形为52.96 mm，最大应力值达到65.2 MPa。

图16 径向注浆管沉降和应力图

如图17所示，管棚法和径向注浆法均能减小衬砌的最大变形，但管棚法的作用更加明显，而径向注浆法对于减小隧道的沉降效果比较差。隧道在穿越断层破碎带时，围岩发生了应力释放和应力重分布，导致断层破碎带受到周围岩层的挤压导致断层破碎带的错动，而管棚法能够有效的防止断层面的错动，而径向注浆法对于断层错动的抑制性较弱。

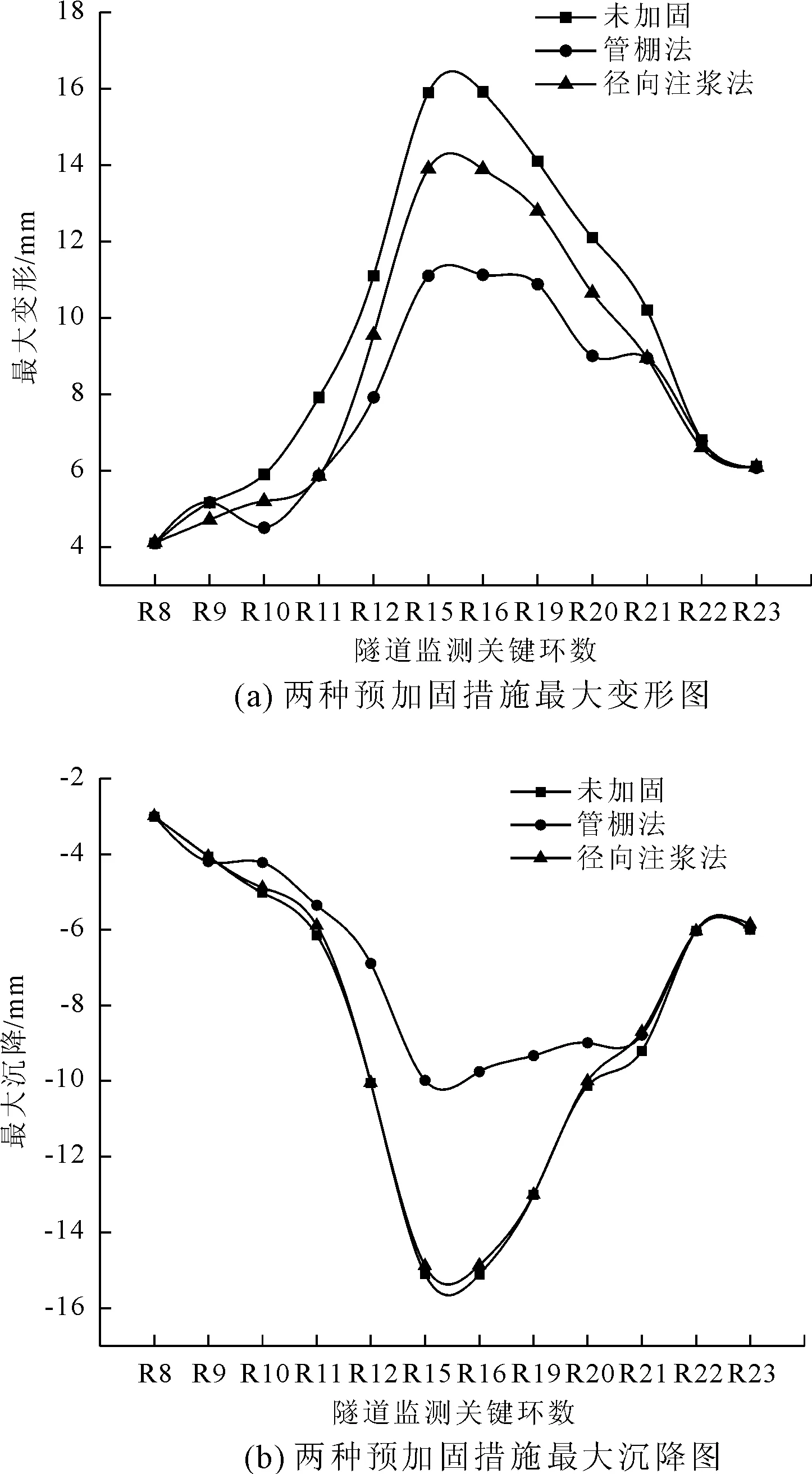
图17 两种不同预加固措施下隧道衬砌的变形图

5 结 论

本研究以某区间盾构隧道穿越断层破碎带为例，考虑注浆压力、顶推力、注浆时效硬化等，建立了详细的三维计算模型。通过解析解的方式验证了数值模型中隧道衬砌内力的可靠性和准确性。通过与Sakurai隧道稳定性的判断方法进行比较，从而判定隧道的安全性。最后，对管棚法和径向注浆法抑制断层错动，减小衬砌变形的效果进行了分析，主要结论如下：

(1) 跨断层隧道的衬砌变形主要受断层的错动影响，衬砌危险点主要分布在进入与退出断层时的节段，即断层面附近的衬砌最危险。衬砌的变形特点主要受断层倾角、宽度和夹角的影响，以72°倾角断层为例，衬砌左拱顶和右拱底压应力较大，容易造成应力集中现象。

(2) Sakurai隧道安全等级能够有效的判断衬砌的安全稳定性，主要采用临界应变和临界应力来分析衬砌及围岩的稳定性，第一和第三危险警告等级分别代表了隧道稳定性的下限值和上限值，超过这个限值的隧道处于临界破坏状态。

(3) 管棚中的超前支护刚管的最大轴力为188 kN，没有超过极限值512 kN，可以继续承担部分荷载，因此可以采用双排甚至多排管棚来防止断层的滑动。径向注浆管的最大变形为52.96 mm，最大应力值达到65.2 MPa，断层的滑动量较大。因此，管棚法和径向注浆法均能有效的减小隧道的最大变形量，但管棚法对于抑制衬砌的沉降变形更加有效。径向注浆法无法有效的阻止断层破碎带的错动。