基于Markov 链优化灰色GM（1，1）模型预测城市居民用电量

陈志恒，王宇凡，熊 昕*

（江汉大学 a. 智能制造学院；b. 人工智能学院，人工智能研究院，湖北 武汉 430056）

0 引言

自新中国成立以来，我国已逐步建成较为完整的能源供给体系。随着信息化时代不断进步，保障经济高速发展的同时兼顾环境保护工作开展势在必行。党的十九大报告中习总书记提出了“金山银山，不如绿水青山”的环保理念［1］，将我国环境保护、资源节约提上工作日程。随着信息化时代不断发展，我国居民的生活质量日益提升，电子设备等高科技产品使用率也逐年增加，用电水平随之提高。因而，电力资源短缺的问题也随之而来。电能作为一种重要的二次能源，由于其不能大规模储存，故电力系统的发电量需随用户用电量的变化而变化。准确预测未来城市对电力的需求量，对城市供电网的完善和规划有重要的指导意义。

近些年，针对预测问题的方法研究，国内外学者提出了大量的预测方法［2-3］，如灰色预测模型、ARIMA 预测模型［4］等。其中，邓聚龙［5］1982 年提出了GM（1，1）预测模型，该模型属于灰色系统理论中的一种预测模型，能够有效处理一些数据较少的序列，在短期预测上有着极为重要的作用。为解决灰色模型在中长期预测中预测精度不高的问题，孙建梅等［6］于2019 年提出利用滑动平均法对原始数据序列进行处理及优化，增强了灰色预测对波动数据序列的抗干扰性，但该方法在处理一些波动较大的数据序列时存在精度不足等问题。为解决由于数据序列波动而导致预测精度不高的问题，陈友华等［7］从信息互补的角度提出组合预测模型。何忠华［8］在2017 年将智能优化算法与灰色模型进行结合，并与传统GM（1，1）模型进行了效果比较，验证了模型具有较好的精度和适用性，但此算法针对数据序列波动较大时，效果不佳且有着较大误差。

本文拟对中国苏州城市居民用电量的历史数据进行分析与利用，建立城市居民用电量的预测模型，并对未来居民用电量进行预测。为避免传统灰色模型在中长期预测上的劣势，针对数据列波动对GM（1，1）模型影响的问题，本文通过引入Markov 概率矩阵来减小波动，建立GM（1，1）-Markov 预测模型以提高模型预测精度，并基于该预测模型对中国苏州市的用电量进行预测，最后与传统灰色模型进行比较。

1 GM（1，1）模型构建

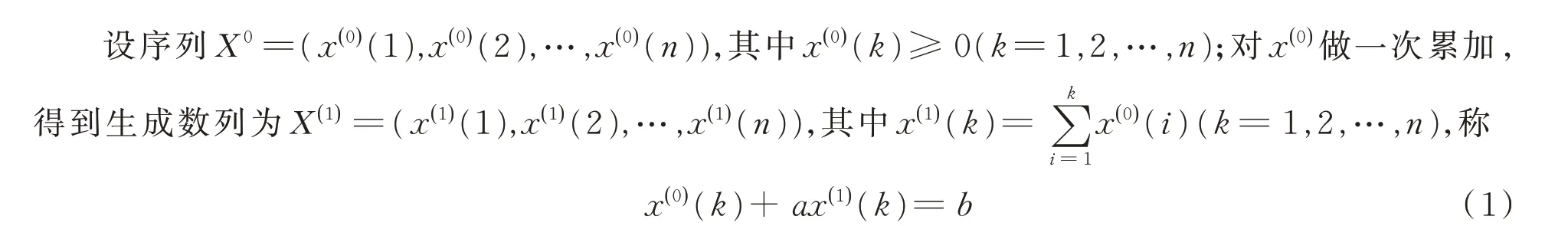
为GM（1，1）模型的原始形式。

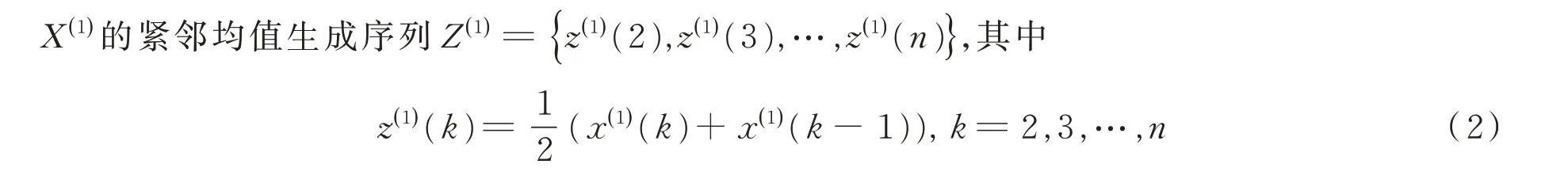
称为一阶线性微分方程。

灰色微分方程为x0(k)+az1(k)=b，由式（2）可得

为灰色微分方程的白化方程。

由式（3）的解可得

2 Markov 链模型

2.1 Markov 过程和Markov 链

Markov 过程是一种随机过程，其中时间参数是离散时间的集合，时间所对应的x(0)(k)也是离散的，且k+ 1 时刻的概率分布只与k时刻的状态有关，与k时刻之前的状态无关，即为Markov链的无后效性［8］，其表示式为

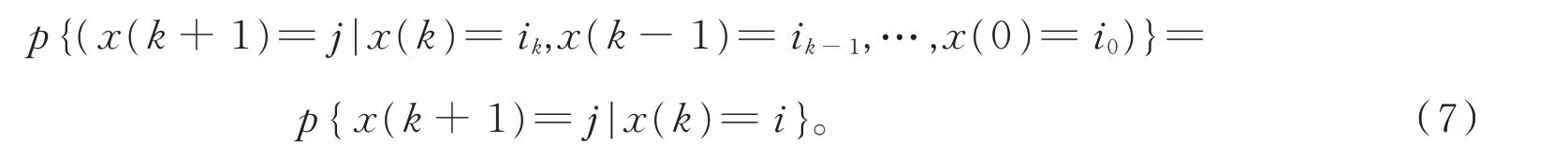
基于Markov 链模型［9-11］，将数据划分成m个状态E1,E2,…,Em。通常分类根据实际数据和GM(1,1)模型预测数据进行划分。本文通过GM（1，1）模型得出预测数据与实际数据之间差值的表达式为

将N0(k)中大于0 的数据令为一个新的数组N1(k)，反之为N2(k)，则

则可将状态指标值的变化区间表示为

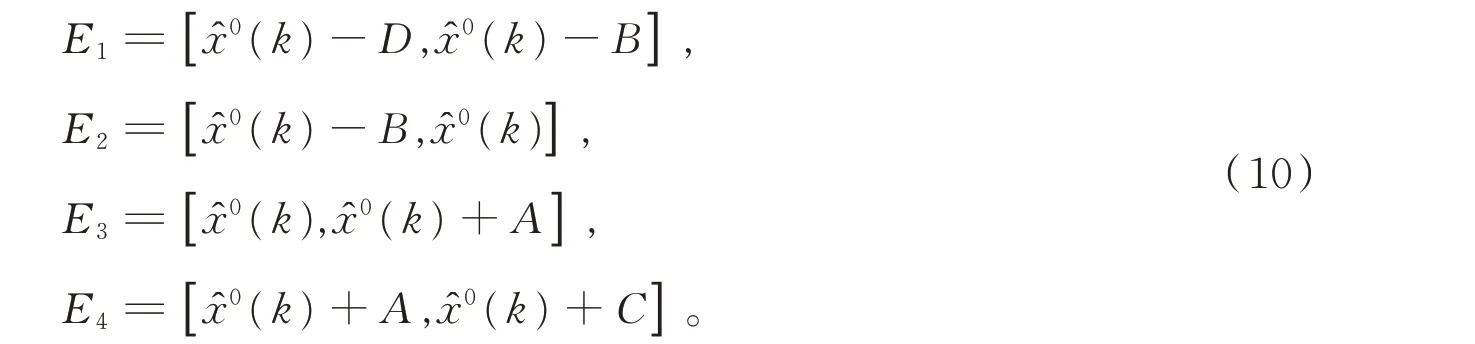
2.2 概率转移矩阵

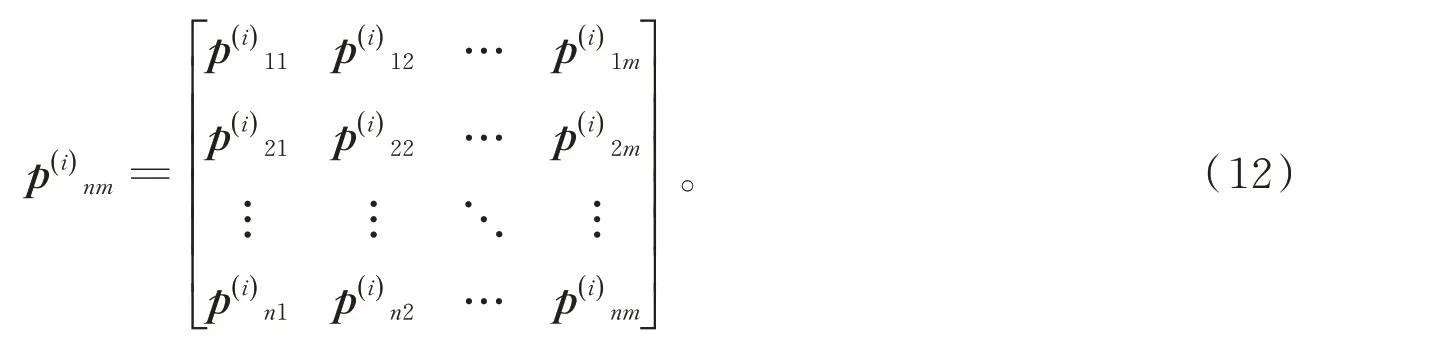
在Markov 链中，系统由一种状态转移到某一种具体状态的可能性用概率来表示，即pnm=p(xn=j|xm=i);n,m∈N*称其为转移概率，即

则称其为一步状态转移概率，即i步转移概率为，则有

2.3 计算各阶自相关系数

用各阶自相关系数来表示各时间段的用电量之间的相关关系及其强弱，阶数是为了预测系统变量而选取的状态转移的步数，即各阶的自相关系数为

对各阶自相关系数进行归一化，即

并将wk作为各种步长的Markov 链的权重。

2.4 计算预测变量处于各状态的概率

将同一状态的各预测概率加权和作为其预测值处于各状态的概率（pi），即

则预测值所对应的状态为max(pi,i∈m)，根据区间得出其预测值为式中，⊗表示其区间范围，u,d∈[A,B,C,D]。

3 预测苏州城市居民用电量

苏州地区属于亚热带季风海洋性气候，四季分明，作为非省会城市其GDP 在国内居前10 名，对用电量需求很大。本文选取苏州市2015 年1 月至2020 年10 月期间每月居民用电量数据［12］作为模型的训练数据（图1），并以2020 年11 月至2021 年3 月中每个月居民用电量（×103GWh）数据作为测试数据测算模型的预测精度。模型达到精度要求后，再用本模型对2021 年4 月的居民用电量进行预测。

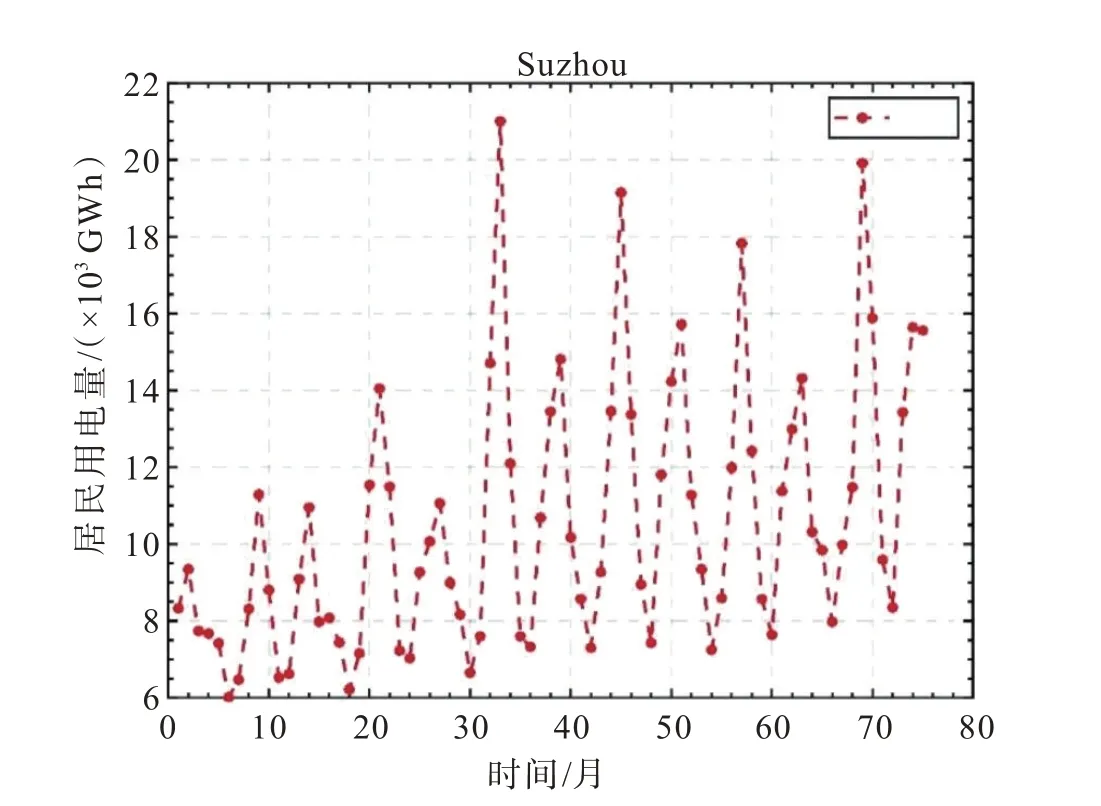
图1 苏州市2015 年1 月-2021 年3 月期间每月的居民用电量数据图Fig.1 The data graph of residential electricity consumption by months in Suzhou from January 2015 to March 2021

使用图1 所示的数据作为灰色模型的原始序列，进行累加生成新的序列X()1，通过表达式（2）～（6），可计算出GM（1，1）模型的时间响应式，即

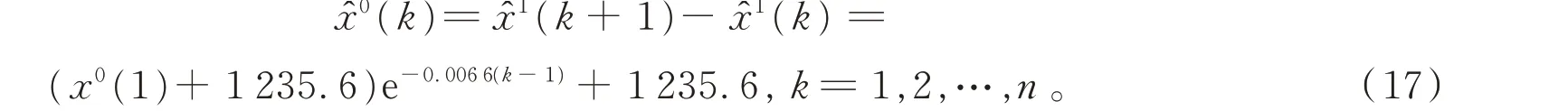
由式（17）可得2020 年11 月-2021 年3 月居民用电量的预测结果，与实际结果的对比见表1。

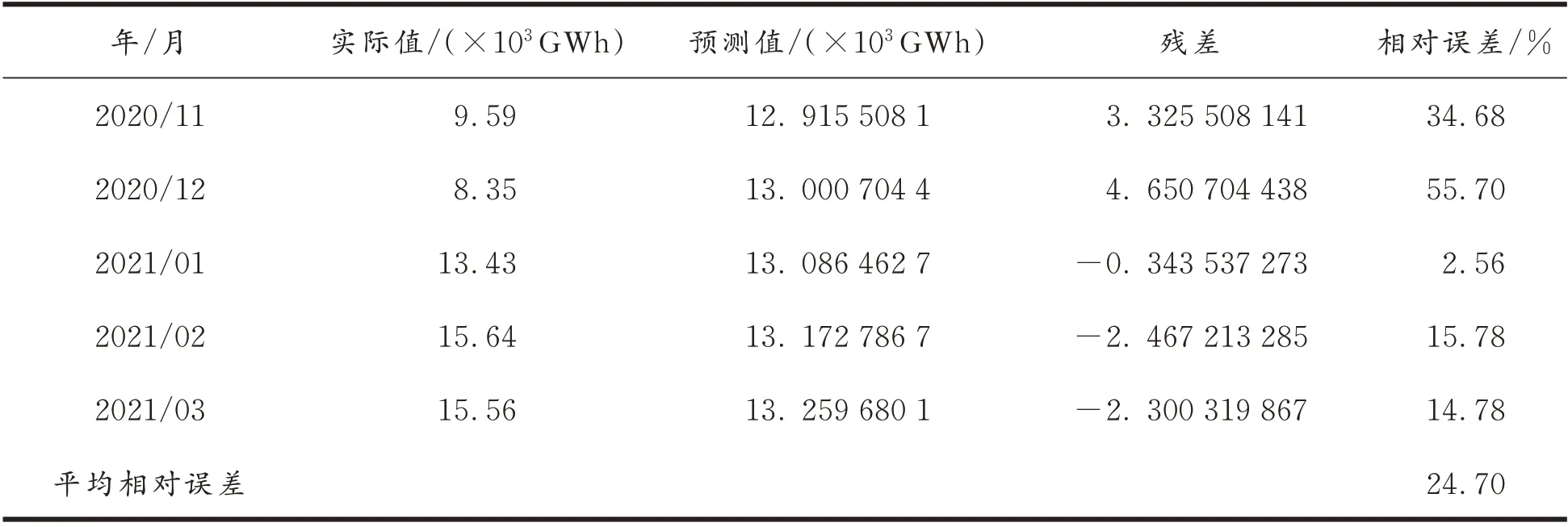
表1 GM（1，1）模型测试数据的预测结果与实际结果的对比Tab.1 The comparisons between predicted results and actual results of the test data of the GM（1，1）model

通过表1 中测试数据的实际值和预测值，使用式（8）和式（9）可计算得出

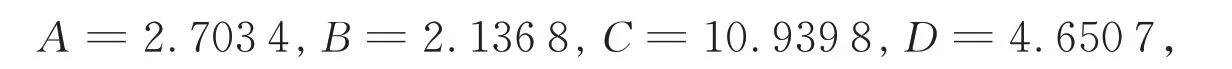
则状态指标值的变化区间表示为

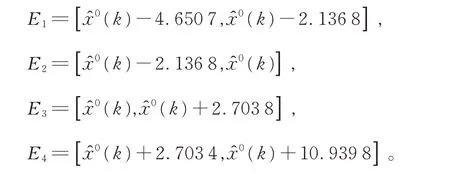
其状态区间划分图如图2 所示。

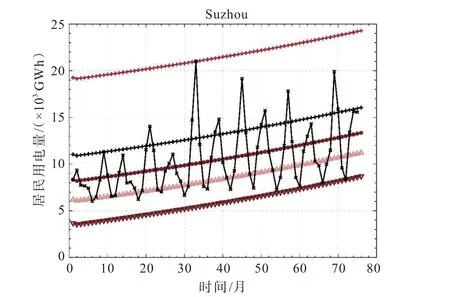
图2 Markov 链系统状态区间划分图Fig.2 The interval partition of the system states on the Markov chain

根据居民用电量对应的状态序列，由式（11）得到Markov 链中状态转移概率矩阵的P44(1),P44(2),P44(3),P44(4)可表示为

由式（13）和式（14）可得测试数据的各阶自相关系数及其权重，分别见表2 和表3。

表2 Markov 链模型计算测试数据的各阶自相关系数Tab.2 The order autocorrelation coefficients of the test data based on the Markov chain model

表3 Markov 链模型计算测试数据的权重Tab.3 The weights of the test data based on the Markov chain model

通过式（15），并根据权重和状态转移矩阵，可得出拟测试月份居民用电量的转移概率，如表4所示。

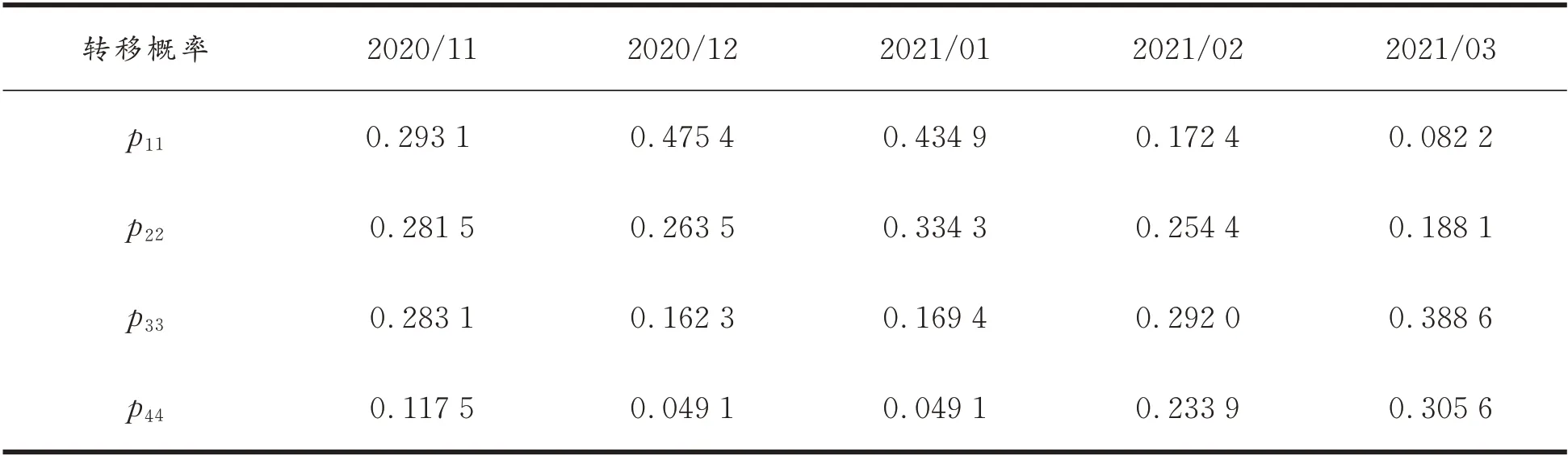
表4 基于Markov 链模型测试月份居民用电量计算测试数据的转移概率Tab.4 The transfer probability of the test data of the residential electricity consumption monthly based on the Markov chain model

最后，通过GM（1，1）-Markov 模型拟合出各测试月份的居民用电量，计算得到相对误差，如表5 所示。

表5 基于GM（1，1）-Markov 链模型测试数据的预测结果与实际结果对比Tab.5 The comparisons of the test data between prediction results and actual results based on the GM（1，1，）-Markov chain model

如图3 所示，GM（1，1）模型在面对数据波动较大时，无法适应实际数据波动。然而，由真实数据曲线可知2021 年1 月相比2020 年12 月的实际数据有较大波动，2021 年1 月的预测数据与实际数据之间有偏差。而2021 年2 月的预测数据通过GM（1，1）-Markov 模型调节后，其预测数据随着实际数据的波动而波动，因此更加证实其实验结果满足了预期要求。

图3 GM（1，1）-Markov 模型和GM（1，1）模型测试数据的结果对比Fig.3 The comparison of the test data results between the GM（1，1）-Markov model and the GM（1，1）model

4 结论

本文通过建立GM（1，1）模型和GM（1，1）-Markov 模型，以苏州市2015 年1 月至2020 年10 月期间每月居民用电量数据作为模型的训练数据，取2020 年11 月至2021 年3 月期间每月居民用电量的数据作为测试数据，从两个模型的拟合对比发现，GM（1，1）模型预测的平均相对误差为24.70%，而通过Markov 链进行优化后其平均相对误差为11.62%。结果表明Markov 链进行优化后的GM（1，1）模型预测效果优于传统的GM（1，1）模型。

GM（1，1）-Markov 模型预测2021 年4 月的苏州市居民用电量为：14.611 379 × 103GWh。苏州市统计局发布2021 年4 月实际居民用电量为10.43 × 103GWh，GM（1，1）-Markov 模型的相对误差为16.36%，与测试数据的平均相对误差相比偏高。实际值与预测值之间有差距，可能是由于苏州市在2021 年3 月份的社会消费品零售额远高于2021 年4 月份的社会消费品零售额，导致电子设备等高科技产品使用率增加，用电量则随之提高。但由于本文模型没有考虑到社会消费品零售额对用电量的影响，后续将引入多种因素约束模型，以达到更好的预测效果，为相关部门的供电调控提供有力依据，减少不必要的能源损耗。