基于混合合并的协作混合自动重传方案

吴 熹

(四川邮电职业技术学院 通信工程学院，四川 成都 610067)

混合自动重传(hybrid automatic repeat request，HARQ)是一种综合应用自动请求重传(automatic repeat request，ARQ)和前向纠错(forward error correction，FEC)的差错控制机制，广泛应用于现代移动通信系统[1]。在不同的性能要求下，系统对错误数据包的处理方式不同。丢弃数据包是一种易于实现的处理方式，然而系统的整体吞吐量较低。另外，错误数据包中含有部分可靠信息，尤其在无线通信环境下，携带了时变信道的特征。有效利用这些信息，可提高系统的通信质量。目前存在两种合并技术——Chase合并(Chase combining，CC)和递增冗余合并(incremental redundancy combining，IR)[2]，它们可以有效解决错误数据包的利用问题。Chase合并的基本思想是每次重传的数据包都是相同的，接收端以信噪比为权值对重传数据进行合并，对信道特性来说则体现为信噪比(signal to noise ratio，SNR)的叠加[3]。IR合并与之有明显的不同，每次重传的数据包均包含不同的冗余版本，在信道估计误差较大或者高阶调制下，具有明显的性能优势[4]。

目前，国内外尝试将HARQ应用于协作通信系统，已取得不少成果[5-10]。Chase合并可以视为重复编码，并不能带来编码增益，而IR合并则在编码技术的推动下体现出更优良的误差性能和更高的吞吐量[11-14]。文献[15]研究了协作环境下二者的性能差异。另一方面，考虑协作系统具有发射分集的特性，在中继链路和信源链路采用不同的合并技术，可以进一步提高系统的差错控制能力和吞吐量。文献[16]给出了一种中继链路和信源链路分别采用IR合并和Chase合并的协作系统模型，证明了信道衰落的概率分布及中断概率下界。仿真结果表明，相对于单一合并技术的协作，HARQ(不管是Chase合并还是IR合并)具有更优的性能。但是，该方案仅适用于较低传输速率的协作系统，在较高传输速率的情况下则力有不逮。

为了解决以上问题，已主要完成了以下工作。

1)提出了基于协作混合自动重传方案的系统模型。在协作阶段，对来自中继链路和信源链路的重传信息分别采用Chase合并和IR合并进行处理。

2)推导出了多个相互独立的指数分布随机变量线性叠加的概率密度函数。在此基础上获得了信道的等效衰落系数，说明了信源信道和中继信道对目的终端的综合影响。

3)推导出了系统的可达容量上界和中断概率下界。通过数值仿真，分析了不同传输速率下系统的中断概率和吞吐量。结果表明，本文所提方案在较高传输速率下改善了系统的性能。

1 协作混合自动重传方案

1.1 系统模型

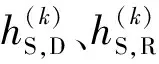
图1 协作HARQ传输模型

1.2 重传方案

本方案分为两个主要的阶段——广播和协作。

广播阶段：当中继未能成功译码时，信源向中继和目的终端采用IR的模式广播数据。

协作阶段：当中继正确译码时，信源和中继同时向目的终端重传信息。信源依然使用IR模式，中继使用CC模式，如图2所示。

图2 n=4时的状态转移图

2 系统性能

2.1 可达容量

广播阶段，信源第i次重传，对中继的信道容量可表达为

(1)

由于广播阶段均采用IR合并，在目的端也具有相同的表达形式。若中继在第n-1次依然不能正确译码，此时为非协作模式，对应的信道容量为

(2)

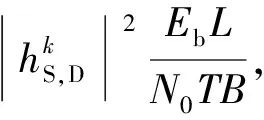
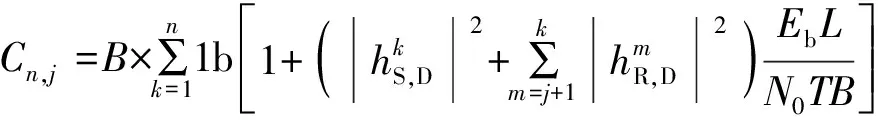
(3)

显然，式(3)得到的是可达容量的上界。

2.2 衰落信道的概率分布

为便于分析衰落信道概率分布，先给出以下命题。

命题1：由多个相互独立参数为σ-2的指数分布随机变量线性叠加的随机变量ξ，其中，加权系数为βk(k=1，2…N)的随机变量有τk个。ξ的概率密度函数为

(4)

(5)

证明：参数为σ-2的指数分布随机变量X的特征函数为

φX(s)=(1-iσ2s)-1

(6)

则Xk=βkX的特征函数和概率密度函数分别为

φXk(s)=φX(βks)=(1-iσ2βks)-1

(7)

(8)

式中，ε(x)为阶跃函数。τk个系数为βk相互独立的指数分布随机变量之和ξk服从Γ分布，特征函数和概率密度函数分别为

φξk(s)=(1-iσ2βks)-τk

(9)

(10)

随机变量ξ的特征函数为

(11)

将式(11)用部分公式展开可得式(12)，参数λk，l可根据文献[17]得：

(12)

由(1-iσ2βks)-l～Γ(l，βkσ2)可以看出，式(12)是由多个Γ分布的随机变量的特征函数构成，由概率密度函数与特征函数互为傅里叶变换的性质可以得到式(4)。命题得证。

式(3)与香农公式存在相似的结构，若定义

(13)

参数η为信道的等效衰落系数，表征的是信源信道和中继信道对目的终端的综合影响。

(14)

显然η由2n-j个相互独立的指数分布随机变量线性叠加而成。

根据命题1的结论，等效衰落系数η的概率密度函数可由式(4)表达，其中各随机变量的加权系数分别为β1=1，βk=2，3，L，n-j。系数为βk的随机变量的个数为τ1=n+1，τk=1(k=2，3，…，n-j)，共有N=n-j种取值。

2.3 中断概率

在2.1节中已经得到非协作模式和协作模式下的可达容量。本节可直接得到系统的中断概率。

中继在第j次传输译码错误的概率为

(15)

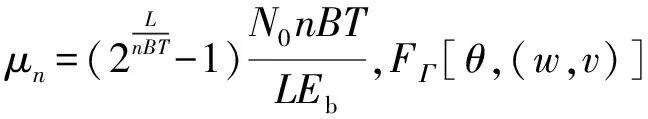
(16)

若中继在第j次参与协作重传，系统的中断概率为

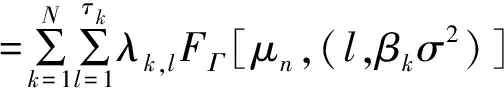
(17)

由式(15)至式(17)可得中断概率的下界

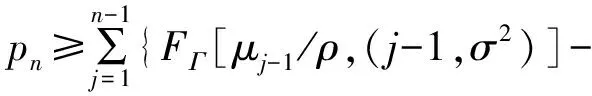
(18)

其中，第一部分表示在中继参与协作下，目的端达到最大传输次数后，仍未能成功解码的概率。第二部分表示中继未能参与协作，终端达到最大传输次数后仍未能成功解码的概率。

3 仿真分析

本节根据最大重传次数n=3的蒙特卡罗仿真结果，将本文方案与文献[16]所提方案进行对比。

3.1 系统中断概率

图3中给出了在系统允许的最低传输速率R=5 b·s-1·Hz-1时的中断概率。当中继距离信源和目的端为等距(ρ=1)时，在中断概率为10-3处，本文提出的传输方案相比文献[16]的方案能获得1.5 dB的性能增益。这是因为广播阶段采用IR合并提高了中继成功译码的概率，从而使得系统更有可能进入协作模式。当中继更靠近信源(ρ=10)时，两种方案的性能差异变小，在中断概率为10-6处，本文方案仅有0.5 dB的性能增益。从此趋势来看，随着中继向信源的逐步靠近，本方案的性能相对文献[16]的方案逐渐变差。这是由于随着中继向信源的靠近，二者之间的信道估计误差减小，IR合并的优势不能体现。在此情况下，Chase合并和IR的性能相当，中继具有相当高的正确译码概率。同时，中继距离目的端相对更远，信道估计误差增大，在此链路上使用Chase合并具有较大的误差。但是这种情况仅在中继非常靠近信源时才会发生。

图3 中断概率下界(R=5 b·s-1·Hz-1)

图4中给出了R=1 b·s-1·Hz-1时的中断概率，中继距离信源和目的端为等距。文献[16]所提方案具有更好的中断概率性能。显然，本文所提方案适用于较高传输速率的协作通信系统，更符合现代通信系统的传输需求。

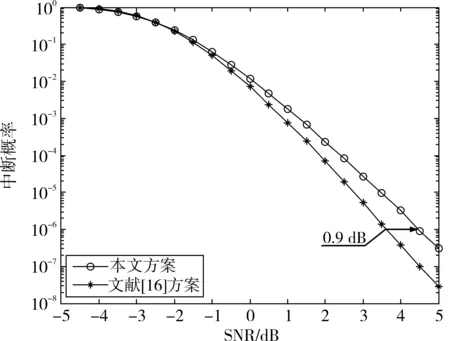
图4 中断概率下界(R=1 b·s-1·Hz-1)

3.2 系统平均吞吐量

由文献[15]可知，平均时延可以用数据包的平均传输次数表示：

(19)

式中，pi表示i次发送后未能成功解码的概率。第一项表示成功解码发生在前n-1次的平均次数，第二项表示前n-1次未能成功解码的平均次数。

平均吞吐量可由下式表达：

(20)

从图5可以看出本文方案具有更高的吞吐量。由于广播阶段采用IR合并，使得中继更有机会参与协作重传，提高了译码成功的概率。由式(19)可以看出，系统具有更低的传输时延，从而式(20)所示吞吐量有所提高。

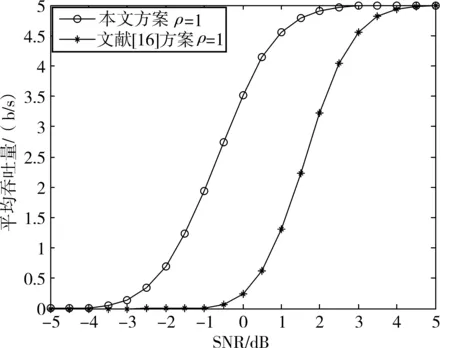
图5 平均吞吐量上界(R=5 b/s)

4 结语

本文提出了一种新的协作混合自动重传方案，目的终端采用Chase合并和IR合并分别对中继链路和信源链路的重传信息进行处理。在理论上分析了采用该方案的协作通信系统能取得的可达容量上界和中断概率下界，并指出了等效衰落信道的概率分布。将本文方案和文献[16]方案进行了仿真对比，结果表明本文方案具有明显的性能优势。另外，在中继距离信源较远时，本文方案也具有较优的性能。