基于自适应可达距离的密度峰值聚类算法

章曼，张正军，冯俊淇，严涛

基于自适应可达距离的密度峰值聚类算法

章曼*，张正军，冯俊淇，严涛

（南京理工大学 理学院，南京 210094）（* 通信作者电子邮箱1277167538@qq.com）

针对基于快速搜索和发现密度峰值的聚类（CFSFDP）算法中截断距离需要人工选取，以及最近邻分配带来的误差导致的在具有不同密度簇的复杂数据集上的聚类效果不佳的问题，提出了一种基于自适应可达距离的密度峰值聚类（ARD-DPC）算法。该算法利用非参数核密度估计方法计算点的局部密度，根据决策图选取聚类中心，并利用自适应可达距离分配数据点，从而得到最终的聚类结果。在4个合成数据集和6个UCI数据集上进行了仿真实验，将所提算法ARD-DPC与基于快速搜索和发现密度峰值的聚类（CFSFDP）、基于密度的噪声应用空间聚类（DBSCAN）、基于密度自适应距离的密度峰聚类（DADPC）算法进行了比较，实验结果表明，相比其他三种算法，ARD-DPC算法在7个数据集上的标准化互信息（NMI）、兰德指数（RI）和F1-measure取得了最大值，在2个数据集分别取得F1-measure和NMI的最大值，只对模糊度较高、聚类特征不明显的Pima数据集聚类效果不佳；同时，ARD-DPC算法在合成数据集上能准确地识别出聚类数目和具有复杂密度的簇。

聚类算法；密度峰值；截断距离；非参数核密度估计；自适应可达距离

0 引言

聚类是数据挖掘和机器学习研究领域中最重要的数据预测和数据分析方法之一。聚类是一种无监督学习方法，目的是使得同一类簇中的元素之间尽可能地相似，而不同类簇中的元素之间尽可能地相异。聚类分析已被广泛用于许多学科领域，涵盖天文学、生物信息学、文献计量学以及模式识别。

随着聚类分析技术的不断发展，研究者们根据实际需要已经提出了许多聚类方法。比如：基于划分的方法，有均值算法（-means）［1］和-中心点算法（-medoids）［2］；基于层次的方法，有利用层次方法的平衡迭代规约和聚类（Balanced Iterative Reducing and Clustering using Hierarchies， BIRCH）［3］和使用动态建模的层次聚类Chameleon［4］；基于密度的方法，有基于密度的噪声应用空间聚类（Density-Based Spatial Clustering of Applications with Noise， DBSCAN）［5］和用于识别聚类的排序点（Ordering Points To identify the Clustering Structure ，OPTICS）［6］。不同的聚类算法能很好地解决某些特定的问题，但总体上仍然存在许多亟待解决的问题，比如聚类效果受数据分布影响较大、复杂度高、聚类数量需要人工干预、聚类效果难以评价等。

2014年，Rodriguez等［7］提出了基于快速搜索和发现密度峰值的聚类（Clustering by Fast Search and Find of Density Peaks， CFSFDP）算法。在算法聚类过程中，聚类的数目会直观地产生，噪声点会自动地被发现并排除在分析之外，而且不管聚类的形状和嵌入空间的维数如何，聚类都会被识别出来。

为了克服这一局限性，已有不少改进算法被提出。如Hou等［8］提出了一种新的局部密度估计方法，该方法仅采用最近邻来估计密度。Mehmood等［9］提出了通过热扩散快速搜索和发现密度峰值聚类（Clustering by Fast Search and Find of Density Peaks via Heat Diffusion， CFSFDP-HD）算法。该算法结合了截断距离选择和核密度估计的边界校正以便更好地估计密度，从而得到更精确的聚类效果，更有效地将聚类点的噪声分离出来。谢国伟等［10］提出了基于非参数核密度估计的密度峰值聚类算法。该算法运用了非参数核密度估计方法来计算数据点的局部密度，避免了截断距离的选取。李涛等［11］提出了基于密度自适应距离的密度峰聚类（Density Peaks Clustering based on Density Adaptive distance，DADPC）算法。该算法基于欧氏距离和自适应相似度，提出了密度自适应距离，能有效地处理簇内同时具有多个密度峰或簇内密度分布相对均匀的复杂结构数据集。

本文提出了一种基于自适应可达距离的密度峰值聚类（Density Peak Clustering based on Adaptive Reachable Distance， ARD-DPC）算法。该算法首先根据统计学原理推导出非参数核密度估计的公式，计算数据点的局部密度，避免截断距离的主观选取；然后考虑到不同密度的聚类中心的可达距离不同，提出一种自适应可达距离的方法分配数据点，有效改善最近邻分配带来的误差问题。在多个数据集上的实验结果表明，本文算法相比原算法具有更好的聚类效果。

1 CFSFDP算法与分析

1.1 CFSFDP算法

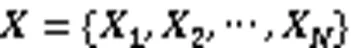
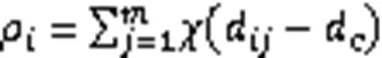
第二种方法是利用Gaussian核，定义如下：

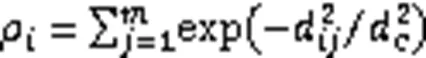
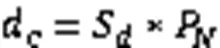
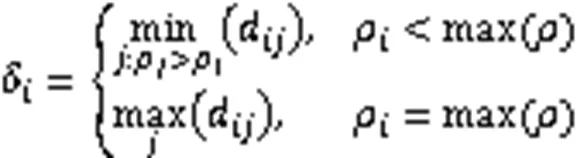
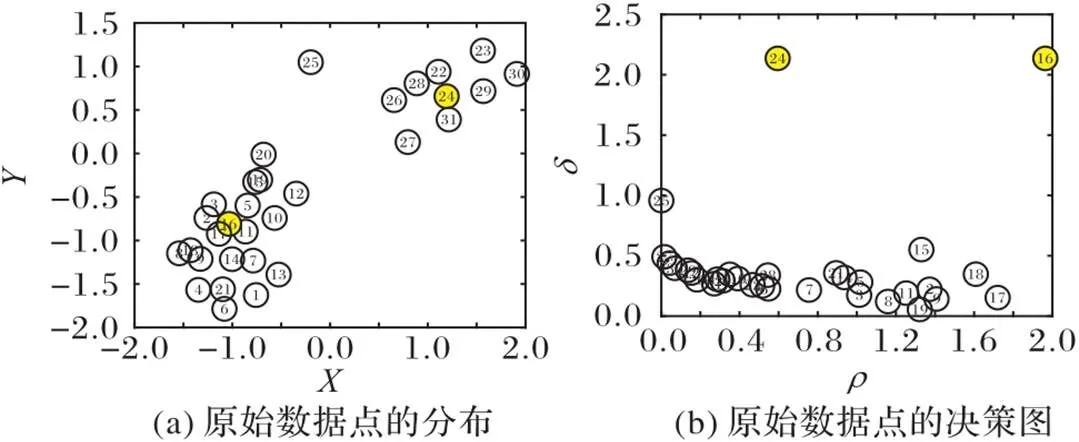
图1 CFSFDP算法的二维展示

1.2 CFSFDP算法的局限性

本文主要针对CFSFDP算法以下两个局限进行讨论：

2）最近邻分配导致的误差问题。CFSFDP算法中，在聚类中心被找到后，将剩余的数据点分配到与聚类中心最近的聚类中。如图2（d）所示，算法虽然正确识别出了3个聚类中心，但是由于近邻分配数据点，导致同一个簇被错误分成3个簇。

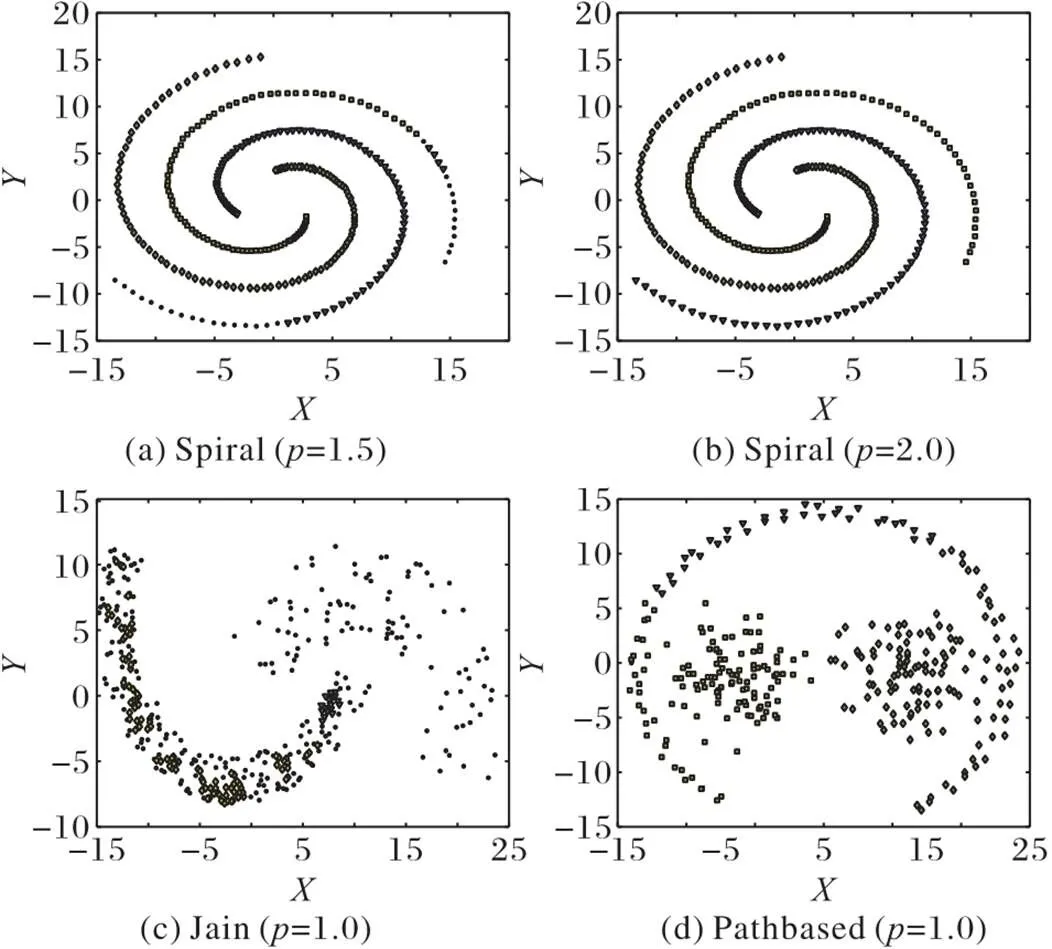
图2 CFSFDP算法在不同合成数据集上的聚类结果

2 ARD‑DPC算法

2.1 非参数核密度估计

非参数核密度估计方法［12］不利用有关数据分布的先验知识，对数据分布不附加任何假定，是一种从数据样本本身出发研究数据分布特征的一种方法。在文献［13］中提到，非参数核密度估计方法已被广泛应用于聚类分析、非参数判别分析、模式识别等方面。在使用基于密度方法的聚类分析中，如果聚类中心被定义为是由这些点构造的密度估计中的模式或峰值，可采用非参数的方法计算局部密度。CFSFDP算法在聚类中心的定义符合上述情况，所以可采用非参数核密度估计的方法用于密度估计。

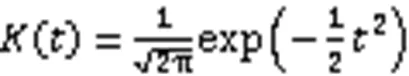
将式（6）代入式（5）中，可以得到核密度估计函数为：

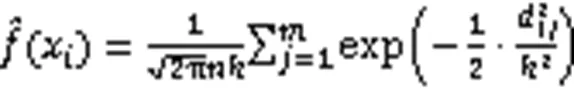
在实际聚类分析的过程中，一般都是多元数据集，所以考虑多元数据集的非参数核密度估计。而多元的性质一般都可以由一元推广得到。

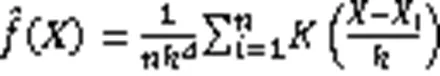
根据文献［13］，不同的核函数的选取也会影响核密度估计的效率。一般的，采用多元Epanechnikov核，此时核密度估计的计算效率最高。多元Epanechnikov核的定义如下：

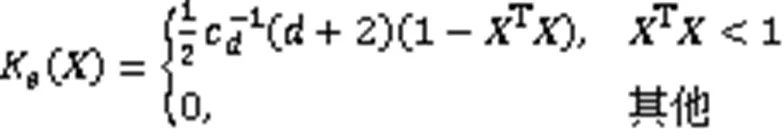
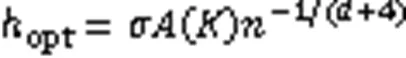
将式（10）代入式（8）可得到多变量的核密度估计：

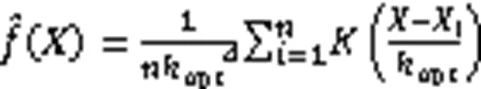
2.2 自适应可达距离

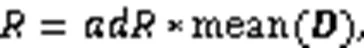
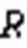
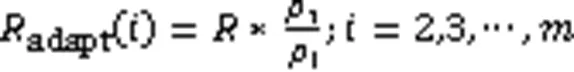
接下来按照自适应可达距离分配数据点，划分簇类，得到最终的聚类结果。首先考虑密度较大的聚类中心，相应的自适应可达距离较小。从第一个聚类中心开始，标记为1，然后根据自适应可达距离遍历其他数据点，数据点在聚类中心的可达距离范围之内，将数据点归到与聚类中心相同的簇中，得到第一个簇；然后再考虑第二个聚类中心，标记为2，根据自适应可达距离遍历剩余数据点，得到第二个簇，一直下去，直到得到最终的簇划分。

2.3 ARD-DPC算法的具体步骤

基于上述分析，ARD-DPC算法的具体步骤如下：

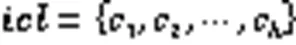
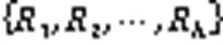
5）划分数据点：

19） end if

20） end while

24） end while

3 实验与结果分析

为了验证本文算法的性能，在Matlab2018a上分别对合成数据集［15］和UCI真实数据集［16］进行了探究实验。实验环境为Windows 10系统，处理器为Intel Core i5-5200U CPU，内存为8.00 GB。

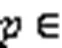
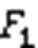
NMI通过将聚类结果与“真实”的类标签对比衡量聚类效果，计算公式如下：

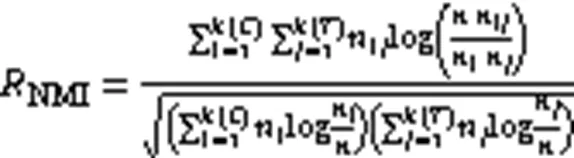
RI评价标准衡量了正确的聚类结果所占的比例，其值越大，划分越佳。计算公式如下：

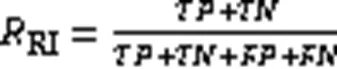
其中：（True Positive）表示应归于同一类，且在结果中被正确地归为同一类；（True Negative）表示应归于不同类，且在结果中被正确地归为不同类；（False Positive）表示应归于不同类，但在结果中被归为同一类；（False Negative）表示应归于同一类，但在结果中被归为不同类。

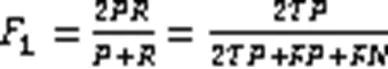
3.1 合成数据集

为了将本文ARD-DPC算法与原CFSFDP算法在具有不同形状簇的复杂数据集上的聚类效果可视化，本文选取了4个二维的具有代表性的合成数据集进行对比实验（图3）。合成数据集的基本信息如表1所示。这些合成数据集的簇的形状各不相同，比如有环状的、流形状的、球状的、块状的等。图3中不同灰度和形状的图形表示不同的类别，算法识别出来的噪声点用黑色圆点表示。

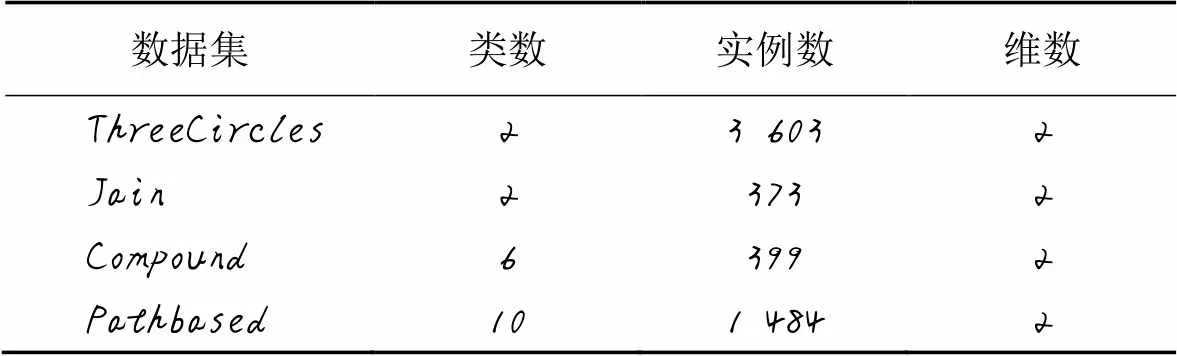
表1 实验中使用的合成数据集

如图3（a）所示：CFSFDP算法没有正确识别出ThreeCircles和Jain的聚类中心，误将聚类的核心点当成噪声点，将属于同一簇类的数据点分成不同的簇，导致聚类划分错误；CFSFDP算法也无法识别出具有不同密度的簇，如Compound，这些簇的形状各不相同，有的高密度的簇被低密度的簇包围，有的低密度簇被高密度的簇包围；对Pathbased，CFSFDP算法虽然正确识别出了聚类中心，但由于最近邻分配，导致同一个簇被错误划分成三个簇。而图3（b）的结果显示，本文的ARD-DPC算法不仅能识别出正确的聚类数，还能识别出任意形状的、具有复杂密度的簇。

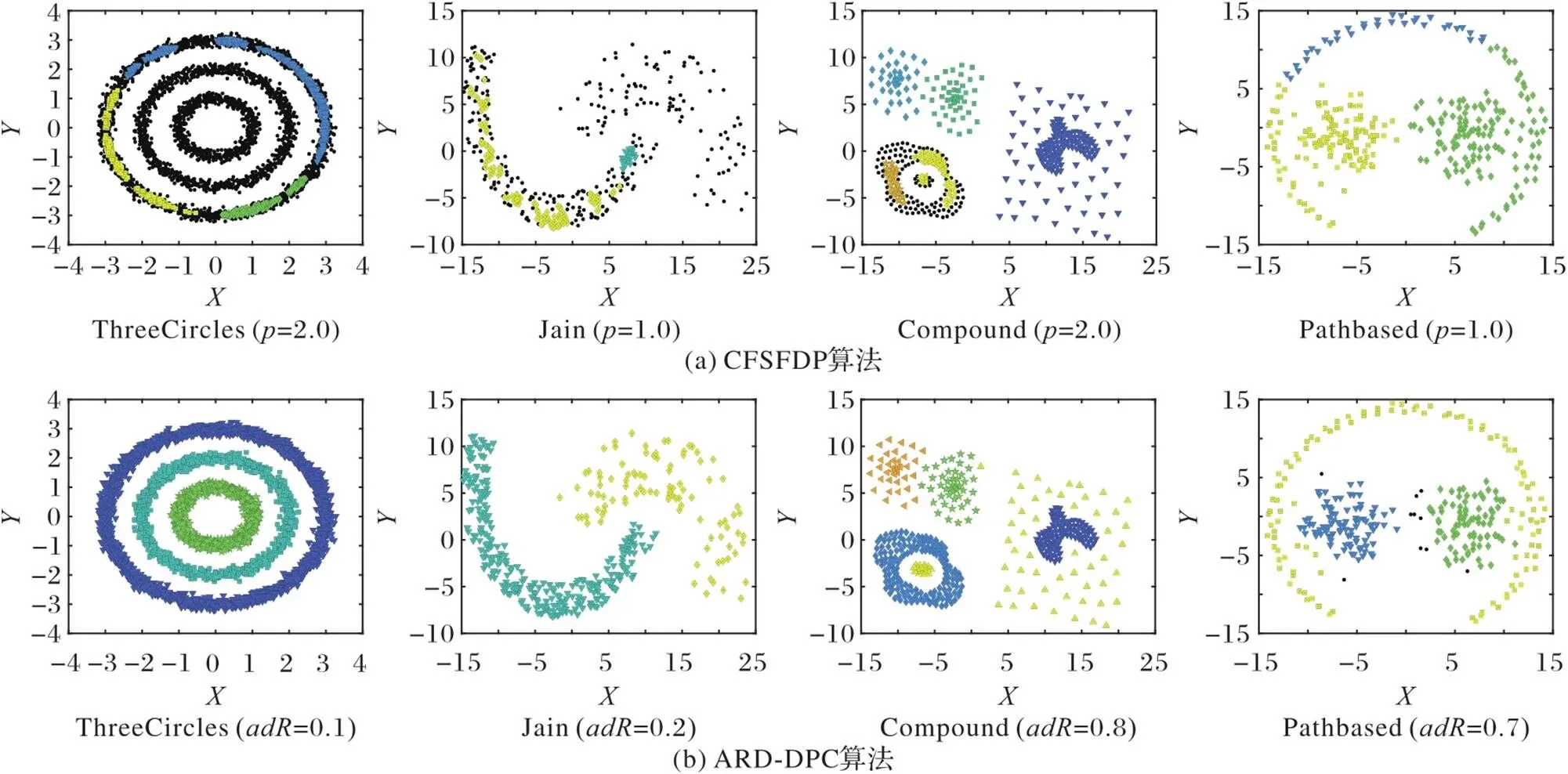
图3 ARD-DPC算法与CFSFDP算法在合成数据集上的聚类结果比较

表2列出了DBSCAN、CFSFDP、DADPC、ARD-DPC这4种算法在4个人工数据集上的聚类性能指标，加粗显示的数据表示在当前数据集中相对最优的指标数据，其中类数比指标代表的是算法最终聚类数与真实聚类数的比值。对比各算法的NMI、RI和F1-measure这三个指标可以发现，ARD-DPC算法在各个数据集上都有着更好的聚类效果。

3.2 UCI真实数据集

为了验证本文ARD-DPC算法在高维数据上的有效性，在6个高维的UCI真实数据集上与DBSCAN算法、CFSFDP算法以及DADPC算法进行对比实验。测试数据集的基本信息如表3所示。由于高维数据难以在二维平面上可视化展示，所以采用NMI、RI和F1-measure评价指标来度量算法的有效性。

表2 四种算法在合成数据集上的评价指标对比

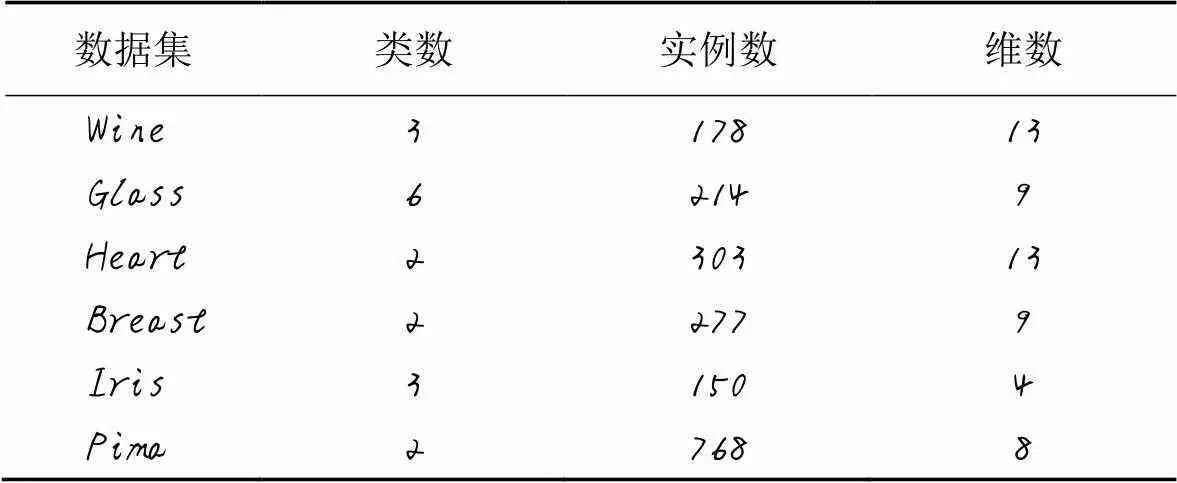
表3 实验中使用的UCI数据集

表4列出了DBSCAN、CFSFDP、DADPC、ARD-DPC这4种算法在6个UCI数据集上的聚类性能指标。对于Wine、Glass和Iris这三个数据集，ARD-DPC算法的三个评价指标均要优于对比算法。这是因为ARD-DPC算法采用了非参数核密度的方法计算数据点的局部密度，避免了截断距离的选取，能够根据聚类中心的密度不同，利用自适应可达距离分配数据点，得到更好的聚类效果。对于Heart数据集，虽然ARD-DPC算法的NMI和RI指标比CFSFDP算法的低，但是F1-measure指标高于CFSFDP算法。可能原因是在Heart数据集中，利用决策图选取的两个聚类中心的密度差不多，所以ARD-DPC算法的聚类效果和CFSFDP算法的效果相差不大。对于Breast数据集，虽然ARD-DPC算法的RI和F1-measure指标略低于DADPC算法，但NMI指标数值约为DADPC算法的两倍。这说明利用ARD-DPC算法得到的聚类结果与真实结果的关联程度更大，可能原因在于采用DADPC算法中的自适应密度距离改变了原数据集的空间分布结构，所以聚类结果与真实结果关联程度不高。对于Pima数据集，ARD-DPC算法的三个评价指标虽然都低于DBSCAN算法，但是高于CFSFDP和DADPC算法。这说明对于Pima这样模糊度较高、聚类特征不明显的数据集，采用密度峰值聚类的算法效果不太好；也有可能是对于高维数据，采用欧氏距离来度量数据之间的相似性不太合理，导致利用决策图无法正确地选择出聚类中心，从而聚类效果不佳。

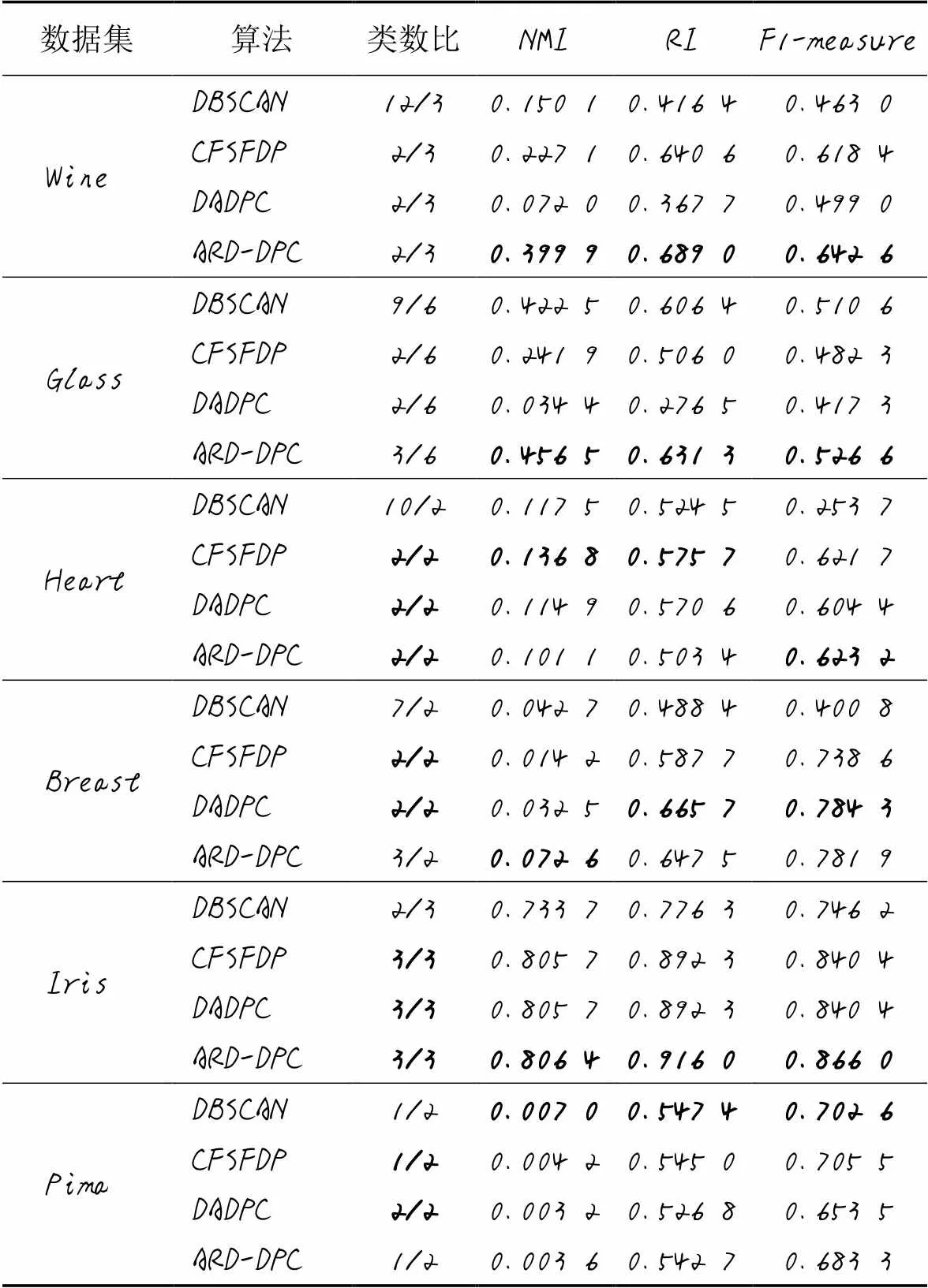
表4 四种算法在UCI数据集上的评价指标对比

综合以上分析可知，与DBSCAN、CFSFDP和DADPC算法相比，ARD-DPC算法在各个数据集上的评价指标都有较大的优势，能更好地识别出实际的聚类数。

3.3 输入参数分析

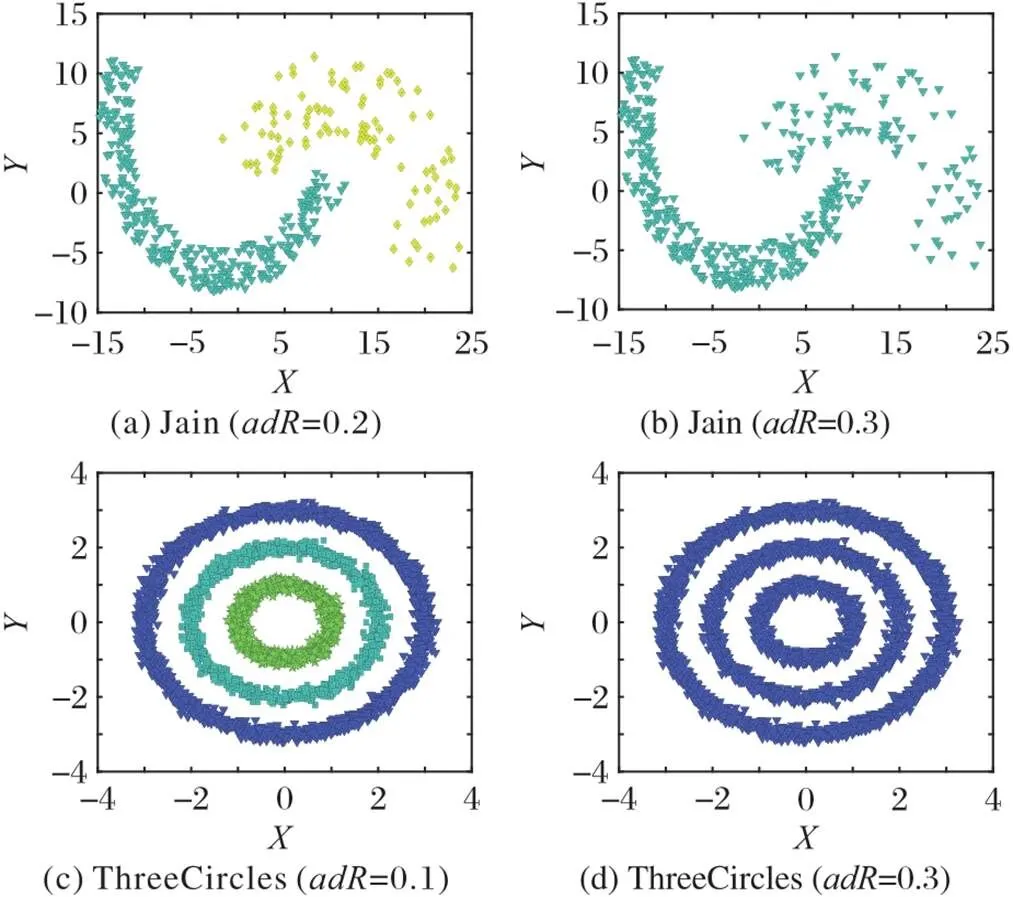
图4 ARD-DPC在合成数据集上的聚类结果

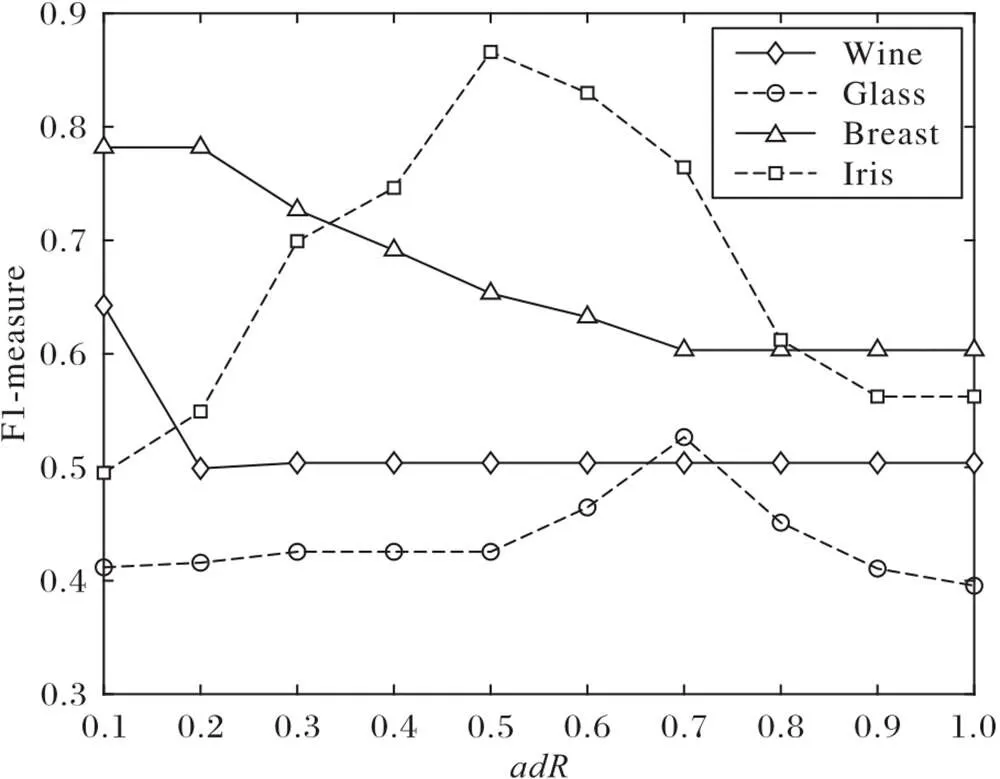
图5 不同adR值时ARD-DPC算法在UCI数据集上的F1-measure

4 结语

本文针对CFSFDP算法中截断距离的难以选取以及最近邻分配误差问题，提出了基于自适应可达距离的密度峰值聚类算法ARD-DPC。实验结果表明，与CFSFDP算法相比，本文提出的ARD-DPC算法具有更好的聚类效果。但是在该算法中，在利用自适应可达距离划分簇类时，需要利用决策图正确识别聚类中心，而自适应可达距离的定义依赖于半径调节参数的选取，以及利用非参数核密度估计数据点的局部密度时，是直接利用固定的带宽值，不能动态地展示每一点的局部密度的变化。因此，下一步要研究如何正确选择聚类中心，定义合理的自适应可达距离的计算方法，以及自适应选择带宽的算法。

[1] MAcQUEEN J. Some methods for classification and analysis of multivariate observations［C］// Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley： University of California Press， 1967： 281-297.

[2] KAUFMAN L， ROUSSEEUW P. Clustering by means of medoids［M］// DOGEE Y. Statistical Data Analysis Based on the L1-norm and Related Methods. Amsterdam： Elsevier Science Publishing Company， 1987： 405-416.

[3] ZHANG T， RAMAKRISHNAN R， LIVNY M. BIRCH： an efficient data clustering method for very large databases［C］// Proceedings of the 1996 ACM SIGMOID International Conference on Management of Data. New York： ACM， 1996： 103-114.

[4] KARPIS G， HAN E H， KUMAR V. Chameleon： hierarchical clustering using dynamic modeling［J］. Computer， 1999， 32（8）：68-75.

[5] ESTER M， KRIEGEL H P， SANDER J， et al. A density-based algorithm for discovering clusters in large spatial databases with noise［C］// Proceedings of the 2nd International Conference on Knowledge Discovery and Data Ming. Menlo Park， CA： AAAI， 1996： 226-231.

[6] ANKERST M， BREUNING M M， KRIEGEL H P， et al. OPTICS： ordering points to identify the clustering structure［C］// Proceedings of the 1999 ACM SGMOD International Conference on Management of Data. New York： ACM， 1999： 49-60.

[7] RODRIGUEZ A， LAIO A. Clustering by fast search and find of density peaks［J］. Science， 2014， 344（6191）： 1492-1496.

[8] HOU J， PELILLO M. A new density kernel in density peak based clustering［C］// Proceedings of the 23rd International Conference on Pattern Recognition. Piscataway： IEEE， 2016： 468-473.

[9] MEHMOOD R， ZHANG G Z， BIE R F， et al. Clustering by fast search and find of density peaks via heat diffusion［J］. Neurocomputing， 2016， 208： 210-217.

[10] 谢国伟，钱雪忠，周世兵. 基于非参数核密度估计的密度峰值聚类算法［J］. 计算机应用研究， 2018， 35（10）：2956-2959.（XIE G W， QIAN X Z， ZHOU S B. Density peak clustering algorithm based on non-parametric kernel density estimation［J］. Application Research of Computers， 2018， 35（10）： 2956-2959.）

[11] 李涛，葛洪伟，苏树智. 基于密度自适应距离的密度峰聚类［J］. 小型微型计算机系统， 2017， 38（6）：1347-1352. （LI T， GE H W， SU S Z. Density peaks clustering based on density adaptive distance［J］. Journal of Chinese Computer Systems. 2017， 38（6）： 1347-1352.）

[12] PARZEN E. On estimation of a probability density function and mode［J］. The Annals of Mathematical Statistics， 1962， 33（3）： 1065-1076.

[13] SILVERMAN B W. Density Estimation for Statistics and Data Analysis［M］. Boca Raton： Chapman and Hall， 1986： 34-117.

[14] 宋宇辰，宋飞燕，孟海东. 基于密度复杂簇聚类算法研究与实现［J］. 计算机工程与应用， 2007， 43（35）：162-165.（SONG Y C， SONG F Y， MENG H D. Research and implementation of density based clustering algorithm for complex clusters［J］. Computer Engineering and Applications， 2007， 43（35）： 162-165.）

[15] DETONE D， MALISIEWICZ T， RABINOVICH A. SuperPoint： self-supervised interest point detection and description［C］//Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Piscataway： IEEE， 2018： 337-349.

[16] DUA D， GRAFF C. UCI machine learning repository［DS/OL］. ［2021-02-20］.http：//archive.ics.uci.edu/ml.

[17] NGUYEN T P Q， KUO R J. Partition-and-merge based fuzzy genetic clustering algorithm for categorical data［J］. Applied Soft Computing， 2019， 75： 254-264.

[18] MANNING C D， RAGHAVAN P， SCHÜTZE H. Introduction to Information Retrieval［M］. Cambridge： Cambridge University Press， 2008： 356-360.

Density peak clustering algorithm based on adaptive reachable distance

ZHANG Man*， ZHANG Zhengjun， FENG Junqi， YAN Tao

（，，210094，）

Concerning the problem that the cutoff distance needs to be selected manually in Clustering by Fast Search and Find of Density Peaks （CFSFDP） algorithm， as well as the poor clustering effect on complex datasets with different density clusters due to the error caused by nearest neighbor assignment， a Density Peak Clustering algorithm based on Adaptive Reachable Distance （ARD-DPC） was proposed. In this algorithm， a non-parametric kernel density estimation method was used to calculate the local density of points， and the clustering centers were selected by the decision graph. Then， an adaptive reachable distance was used to assign the data points and obtain the final clustering result. Simulation experiments were conducted on 4 synthetic datasets and 6 UCI datasets， and the proposed algorithm was compared with CFSFDP （Clustering by Fast Search and Find of Density Peaks）， DBSCAN （Density-Based Spatial Clustering of Applications with Noise） and DADPC （Density Peaks Clustering based on Density Adaptive distance）. Experimental results show that compared to the three other algorithms， the proposed ARD-DPC algorithm achieves the all highest Normalized Mutual Information （NMI）， Rand Index （RI） and F1-measure on 4 synthetic datasets and 3 UCI datasets， the only highest NMI on UCI Breast dataset， the only highest F1-measure on UCI Heart dataset， but does not cluster UCI Pima dataset well， which has high fuzzyness and unclear clustering feature. At the same time， ARD-DPC algorithm can accurately identify the number of clusters and clusters with complex density on the synthetic datasets.

clustering algorithm; density peak; cutoff distance; non-parametric kernel density estimation; adaptive reachable distance

This work is partially supported by National Natural Science Foundation of China （11671205）.

ZHANG Man， born in 1998， M. S. candidate. Her research interests include machine learning， data mining.

ZHANG Zhengjun， born in 1965， Ph. D.， associate professor. His research interests include data mining， graphics technology， image processing.

FENG Junqi， born in 1997， M. S. candidate. His research interests include machine learning， data mining.

YAN Tao， born in 1977， Ph. D.， associate professor. His research interests include linear and nonlinear programming， optimization models and algorithms in application problems， complementarity problems， programming with equilibrium constraints.

TP301.6

A

1001-9081（2022）06-1914-08

10.11772/j.issn.1001-9081.2021040551

2021⁃04⁃12；

2021⁃07⁃22；

2021⁃08⁃05。

国家自然科学基金资助项目（11671205）

章曼（1998—），女，安徽太湖人，硕士研究生，主要研究方向：机器学习、数据挖掘；张正军（1965—），男，江苏阜宁人，副教授，博士，主要研究方向：数据挖掘、图形技术、图像处理；冯俊淇（1997—），男，辽宁沈阳人，硕士研究生，主要研究方向：机器学习、数据挖掘；严涛（1977—），江苏泰兴人，副教授，博士，主要研究方向：线性与非线性规划、应用问题中的优化模型及算法、互补问题、均衡约束规划。