水下缆索运动建模与仿真分析方法

张 斌，刘延平

（1. 中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003；2. 清江创新中心，湖北 武汉 430076）

0 引言

随着对海洋开发利用的不断深入，各类水下无人锚泊驻留系统、海洋拖曳系统逐渐成为相关热点研究领域，准确预报分析锚泊、拖曳等系统在海流等外界环境扰动下的动态运动响应成为其工程设计的关键。其中，建立用于连接设备、传递或缓冲载荷、传输能源和信号等用途的柔性缆索的运动学与动力学精确建模是一项难点技术。

水下柔性缆索的力学、运动学特征与锚泊、拖曳系统整体状态耦合相关，并交互影响，且随着外部载荷变化呈现非线性时变状态，难以对描述其状态的微分方程进行直接求解，通常在满足动力学条件和连续性条件下，采用有限差分[1-2]、集中质量[3-4]、有限段[5-6]等空间域内的物理离散方法对连续缆索控制方程进行近似求解。

在水下缆索中内部张力占主导作用情况下，可忽略缆索单元空间旋转运动，上述线性离散化求解方法可取得较好的计算精度和准确性。但在处理多点悬链系留、锚泊状态振荡急剧变化、拖船大范围转向等易于出现缆索低张力松弛、非线性大形变等问题时，线性离散单元无法准确反映描述缆索空间曲率引起的弯矩、扭矩作用，难以描述缆索真实空间状态与内力状态，进而出现数值求解奇异。通过选取大量离散节点进行更加细的线性单元划分来逐渐逼近缆索真实轮廓，不仅算力消耗剧增，也面临数值积分截断误差与舍入误差累加问题导致的计算错误。

因此，本文改进柔性缆索的线性离散化单元为高阶非线性单元，采用三次样条插值描述缆索微元的空间形态，通过加权余量法解决插值方法仅能在离散节点位置满足缆索状态微分方程问题，消除微元长度范围内残差，提供一种高效、准确求解水下缆索复杂运动状态的新方法。

1 水下缆索空间运动数学模型

引入图1中所示的惯性坐标系O（xe，ye，ze）、缆索局部坐标系 S（q1，q2，q3）以及弗莱纳坐标系 S（t，n，b）。

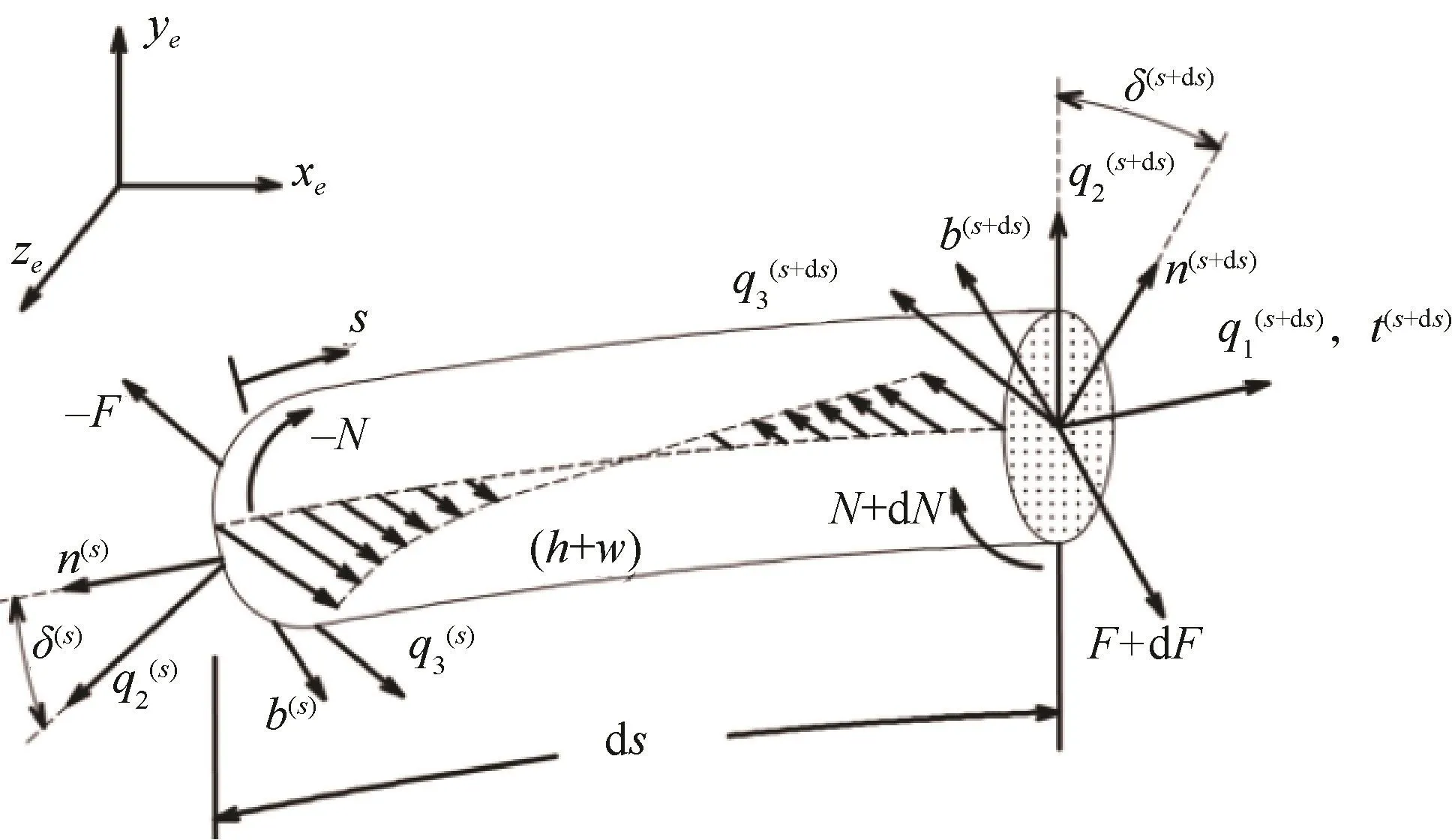
图1 坐标系选取及水下缆索微元力学状态Fig.1 Coordinate systems involved and micro-elements force of the cable element

对于长度为ds的缆索微元，其在流体作用力、自身体积力、内部张力等共同作用下，大地坐标系中空间平移与旋转运动的微分控制方程如下[7]：

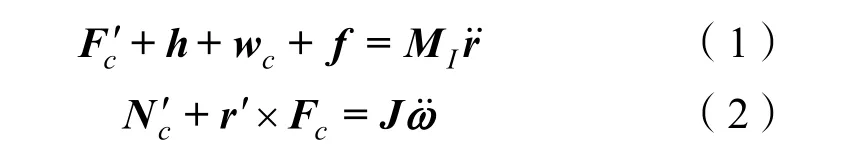
式中：Fc为微元内部张力矢量；h为微元长度上的流体作用力；wc为微元水下湿重矢量；f为其他外部作用力；MI为缆索微元质量矩阵；r（s，t）为缆索微元的空间构型曲线矢量；Nc为微元内部的弯矩、扭矩矢量；ω为缆索微元的旋转角速度矢量阵。

应综合考虑坐标系S（q1，q2，q3）以及S（t，n，b）本身不重合导致的角间距 δ（s，t）偏差，与缆索微元形状扭转变形共同组成总挠率[8]：

缆索微元内部任一点处力矩矢量可表述为沿弗莱纳坐标系 b轴方向的弯矩以及沿 t轴方向的扭矩[9]：

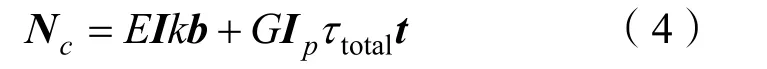
式中：I为缆索横截面惯性矩；Ip为缆索横截面极惯性矩；G为缆索的材料剪切模量。

水下缆索大长细特性使得其转动惯量矩阵 J本身较小，且其法向阻力系数一般以量级差距远大于切向阻力系数，进一步限制其产生旋转角加速度，大地坐标系中其旋转控制方程等式右半部分为2个极小值乘积，可认为水下缆索微元内部力与力矩形成近似平衡状态，可得：

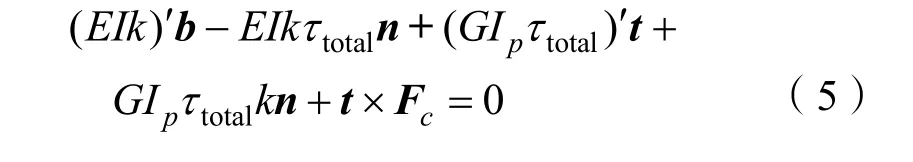
与弗莱纳坐标系单位矢量t叉乘，去除上述旋转运动控制方程中沿切向t并对内部力矩无影响分量部分，可得：

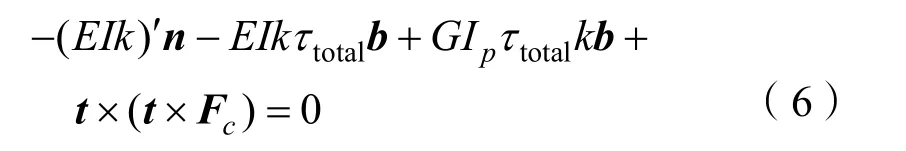
通过叉乘反交换率与拉格朗日公式计算上式中连续叉乘，可得到沿水下缆索微元轴向任意位置处的内部张力矢量：

式中，TC为缆索内部轴向拉力。

通过水下缆索微元空间构型曲线r(s, t)描述弗莱纳坐标系各轴线矢量方向，具体形式如下：

可将内部力 FC从弗莱纳坐标系中转换至大地坐标系中，简化对于弯曲、扭转等力矩作用效果的求解。

水下缆索微元大地坐标系中空间平移运动方程可写为如下形式，包含了微元中轴向拉力、扭转应力、弯曲应力对于缆索空间形态r(s, t)的影响：

由于水下缆索中扭矩沿轴向连续且恒定，可知旋转运动控制方程在弗莱纳坐标系t轴方向投影必定为0：

上式给出了坐标系S（q1，q2，q3）以及S（t，n，b）本身不重合导致的角间距 δ（s，t）偏差的计算方法，进而可以确定坐标系 S（q1，q2，q3）的坐标轴指向。

2 水下缆索运动控制方程离散化求解

2.1 水下缆索非线性离散化单元构造

由连续缆索运动控制方程计算推导过程可知，坐标系矢量轴方向、缆索形变量均可通过缆索空间形态r（s，t）及角间距δ（s，t）求解得到。

在空间域内对水下缆索进行离散化处理，将其划分为N段长度为ds的非线性高阶单元。根据[A1]大地坐标系下节点坐标值 r（i）（i=1，2…N，N+1）通过3次样条差值方法构造试函数逼近空间样条曲线的真实分布状态，二阶连续可导既满足空间曲率连续要求，又能避免更高阶函数带来的额外方程求解问题。

图2 水下缆索非线性单元划分Fig.2 Non-linear element of the underwater cable

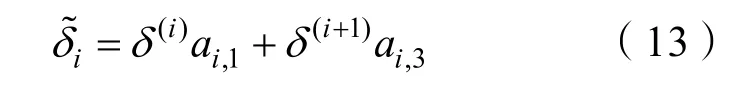
2.2 加权余量法求解

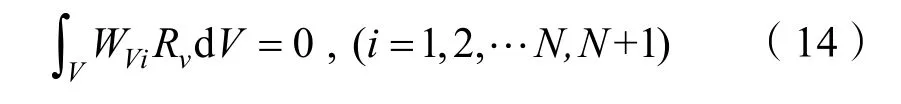
式中：Wvi是求解域内的权函数；Rv为试函数偏差产生的计算残数；V为去除边界后的求解计算域。

选用Galerkin方法为求解具体方法，其权函数与基函数一致，可将微分方程转换为一系列对称的代数方程，实现计算收敛的同时进一步减小算力需求。对于第i（i=1，2…N，N+1）段非线性缆索微元，其计算域内的余量消除方程为

受篇幅所限，缆索单元求解域内部张力、流体力、体积力、弯曲力、扭转力等矩阵的具体形式不再赘述[11-12]。

方程（17）-（18）完整描述了每一段缆索单元空间平移与旋转运动。对于缆索节点i，其广义运动速度和加速度在其前后两段缆索单元运动控制方程中体现，将第i-1段、第i段单元中关于节点i的相关项叠加整合，可得节点1至节点N处运动方程：

式中：[H]、[W]、[B]为各离散节点叠加整合后的流体作用力、缆索质量及浮力矩阵；[M]为（3N+3）阶质量矩阵；[KAXIA]、[KBEND]、[KTORQ]为各离散节点叠加整合后的轴向张力、弯曲作用力、扭转作用力矩阵，为（3N+3）×（6N+6）阶形式矩阵。

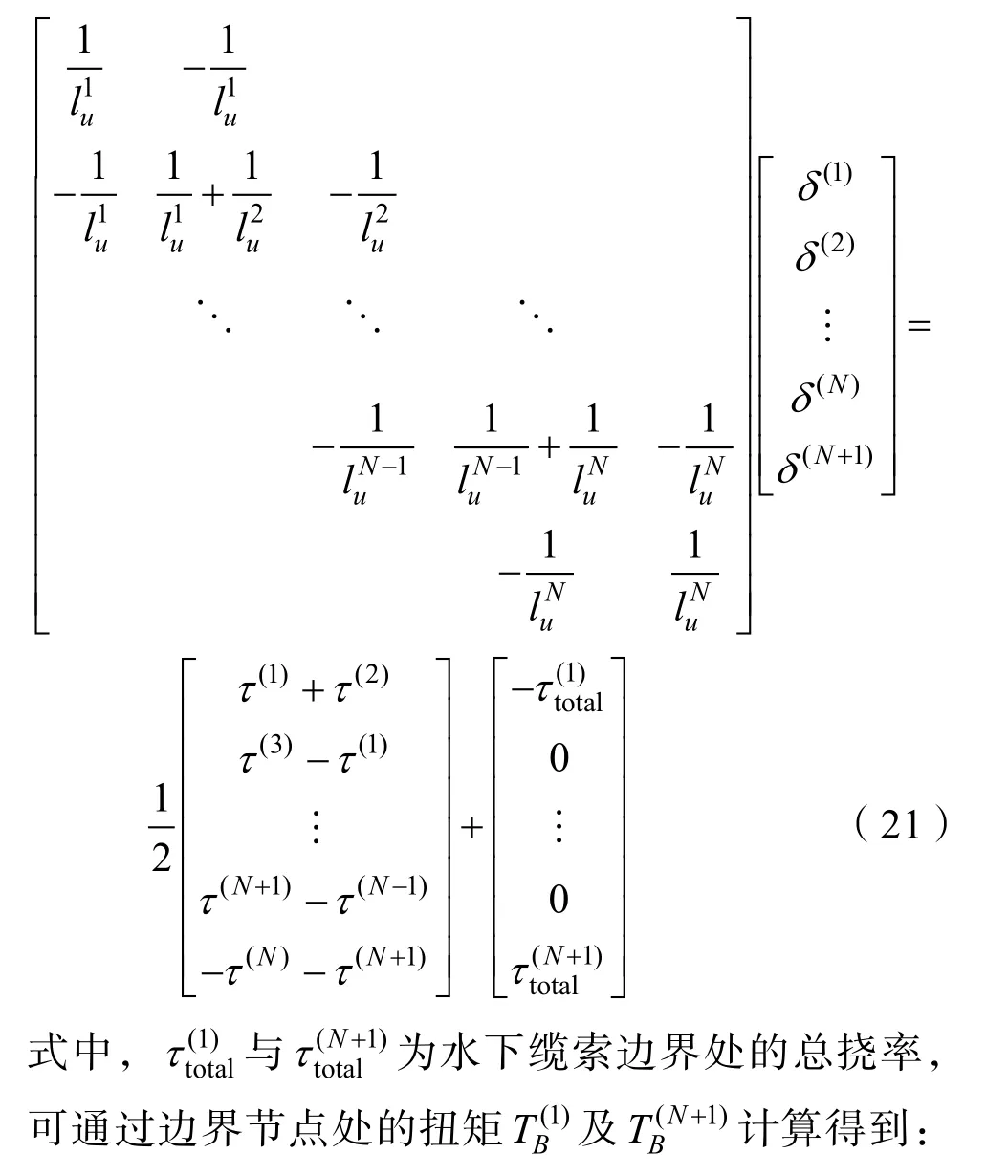
对于常见的水下锚泊系统、拖曳系统，缆索上一般无外部额外施加力矩，因此，可将非线性缆索单元的扭转运动约束方程整合为如下形式，计算中需指定水下缆索首节点扭转形变角δ（1）或末节点处扭转形变角 δ（N+1）以固定一个扭转自由度，使得该约束方程左侧系数矩阵变为满秩矩阵，进而获得唯一解。

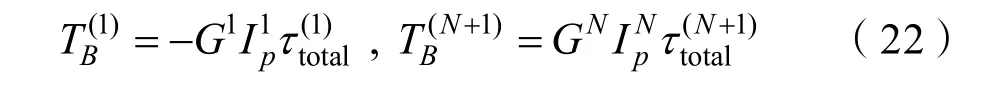
3 模型验证

3.1 Hopland拖曳试验验证

采用1992年Hopland进行的通信光缆拖曳布放实海实验测试数据作为对比算例[13]，通过水下缆索运动模型对其重型铠装拖缆在拖船加减速过程中动态变化情况。

该缆索主要物理特性如下：直径33.2 mm，总长 300 m，密度 3 121 kg/m3，弹性模量77.5×109Pa，抗弯刚度1 000 N·m2，法向阻力系数1.649，切向阻力系数0.12。

加速实验过程中，拖船以约1.1 kn匀航速拖动缆索达到稳定状态，随后进入加速拖曳阶段，拖船速度在60 s时间内均匀增大至2.4 kn。计算模型仿真计算结果如图3所示，图中，t=0时刻的缆形图对应于1.1 kn均匀航速拖曳下缆索状态，t=60 s时刻，拖船线性加速达到2.4 kn，由仿真结果可知，拖缆其重新趋于稳态时间滞后约360 s。

图3 拖船加速过程HA缆姿态变化Fig.3 Attitude change of HA cable during the towing ship accelerating process

减速实验过程中，拖船以约2.5 kn匀航速拖动缆索达到稳定状态，随后进入减速拖曳阶段，拖船速度在60 s时间内均匀降低至1.0 kn。计算模型仿真计算结果如图4所示，图中t=0时刻的缆形图对应于2.5 kn均匀航速拖曳下缆索状态，t=60 s时刻，拖船线性减速达到1.0 kn，由仿真结果可知，拖缆重新趋于稳态时间滞后约460 s。

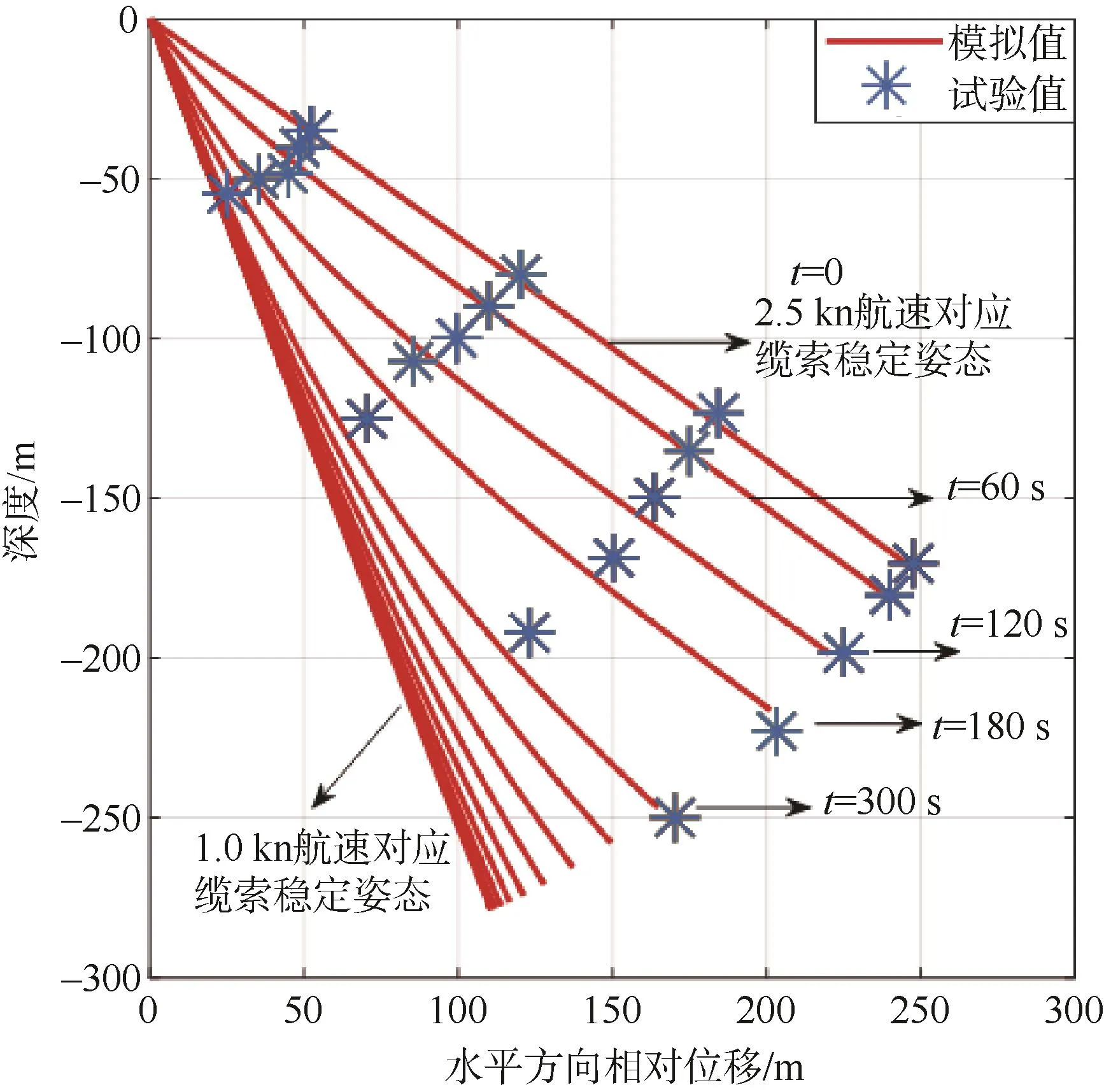
图4 拖船减速过程HA缆姿态变化Fig.4 Attitude change of HA cable during the towing ship decelerating process

综合上述实验测试缆索形态变化及 Hopland实测的缆索节点空间位置坐标，可以看到数值模拟数据与实验数据吻合度及变化规律高度一致，仅存在细微偏差，推测是由于实验测量误差及实验过程中海流流速影响等导致。

3.2 细长柔性杆件弯曲形变计算验证

通过与可精确求得解析值的经典细长柔性杆件受力弯曲形变模型进行比对分析，验证本计算模型中高阶非线性微元划分及加权余量方法消除残差趋近物理模型真实空间形态方法的准确性，也直接对模型中弯曲应力的影响结果进行比对分析。

本算例的物理模型为一端固定约束、一段自由的细长柔性杆件，对其末端施加竖直向下集中载荷P。由材料力学相关解析求解方法可知，细长杆上任一点处曲率半径如下：

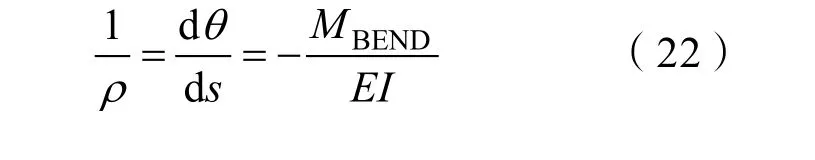
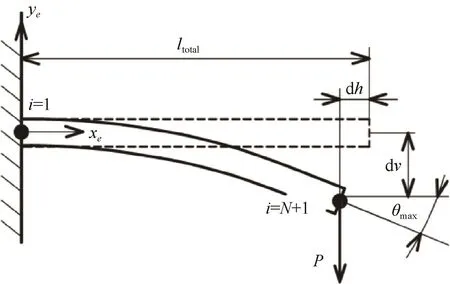
图5 细长柔性杆件弯曲形变计算验证模型Fig.5 Bending deformation validation model of flexible rod

式中：MBEND为该点位置弯矩；E为材料弹性模量；I为杆件的横截面惯性矩；θ为该点弯曲形变后绕中心轴转动角度；s为挠度曲线弧长。

上述末端节点的位移量、偏转角可通过数值积分求解方法获得准确值。

本算例模型相关计算参数如下：直径20 mm、长度10 m、密度1 000 kg/m3、弹性模量2×1011Pa。采用高阶非线性离散化模型建立杆件的运动控制方程，仿真分析不同集中力载荷P施加状态下杆件形态及末端节点坐标值，具体结果如图6所示。

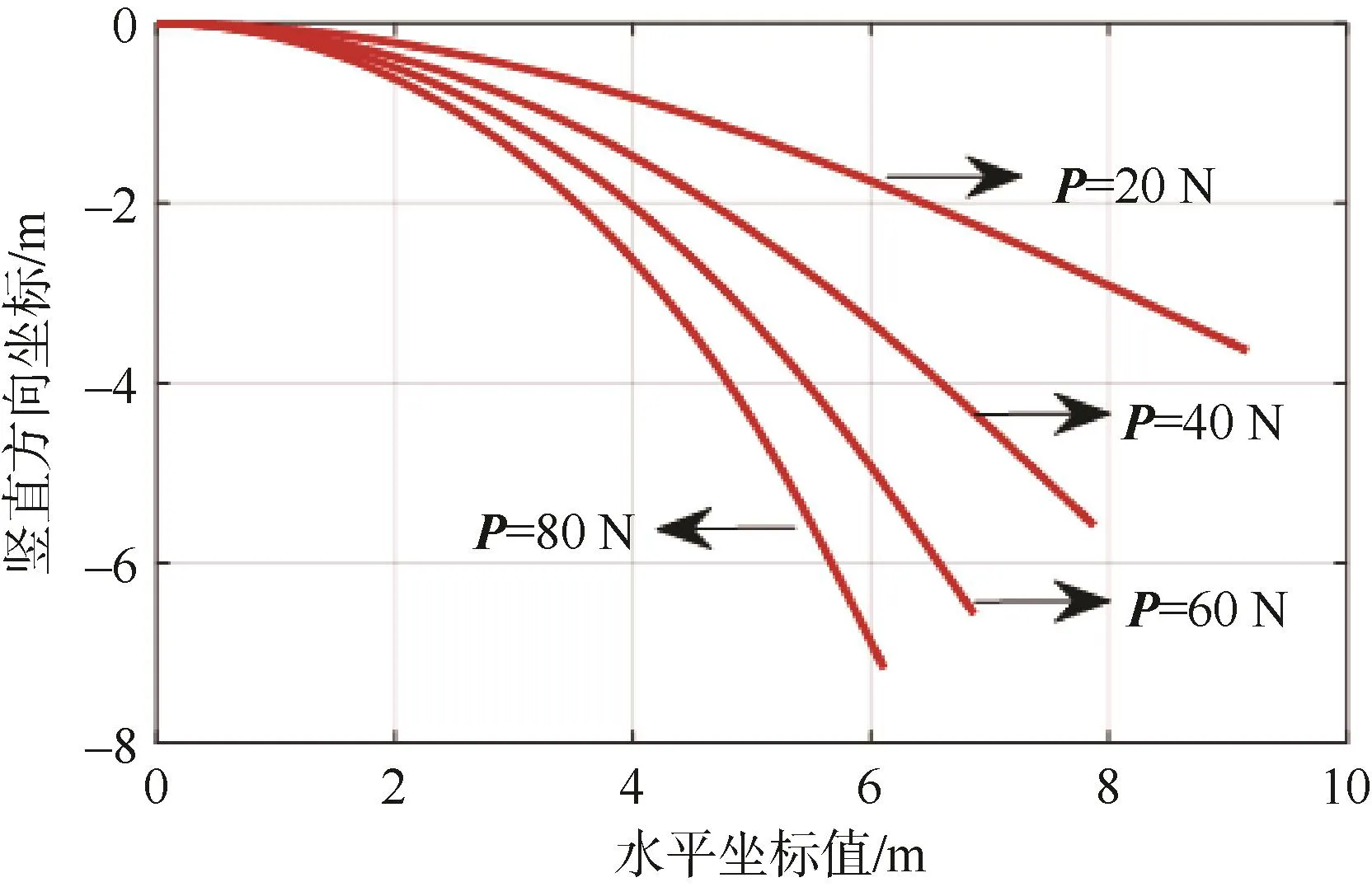
图6 不同集中载荷作用下细长杆平衡姿态Fig.6 Torque equilibrium attitude of the flexible rod with different loading

图7 末端节点坐标值随时间变化情况Fig.7 Change of the end node’s coordinate value with time

图8 杆件形态随时间变化情况（Δt=2 s）Fig.8 Change of the attitude of the flexible rod with time（Δt=2 s）

由计算结果可知，杆件末端节点在集中载荷P的作用下逐渐偏转，在弯曲应力与载荷P共同作用下，节点在平衡位置附近做欠阻尼振荡并逐渐趋于稳定状态。

不同计算约束条件下，使用本文建立的运动控制模型求解得到的末端节点坐标值与解析值结果相对误差ε如下表所示，具体计算方法为

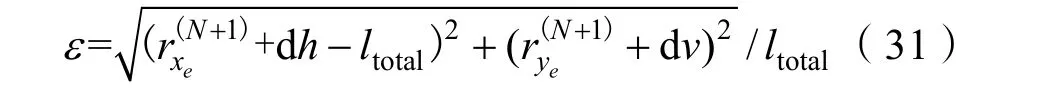
由计算结果可知，通过高阶非线性微元物理离散方法建立的运动控制方程具有较高计算精度。

表1 细长柔性杆件弯曲形变计算结果比对Table 1 Comparison of the simulation value and theoretical value of the flexible rod

4 结束语

本文将水下缆索线性化离散改进为高阶非线性单元，建立了包含弯矩、扭矩作用的水下缆索状态微分方程数值求解模型，通过与Hopland水下缆索拖曳试验数据、细长柔性杆件弯曲形变计算等对比分析，验证了本文高阶离散求解模型的准确性，可为水下锚泊系留、水下拖曳等系统复杂运动状态高效求解与工程设计提供有价值的参考。