小口径高炮修正弹在脉冲作用下的运动特性

2022-07-05杨志伟王良明陈健伟殷永旸

兵工学报 2022年6期

杨志伟，王良明，陈健伟，殷永旸

(南京理工大学能源与动力工程学院，江苏南京 210094)

0 引言

小口径高炮是目前用于近程防空的主要武器之一。由于小口径高炮具有初速高、射界大、射速快和射击精度高的优点，其作为防空系统中的最后一道防线在军队中大量装备。然而，随着现代超音速导弹突防能力的提升，小口径高炮的打击精度和打击能力已无法满足实际需求。提升小口径高炮打击精度和打击能力的方法有很多，如为高炮装备高精度的光学瞄准镜、炮瞄雷达、热像仪和射击指挥仪等设备，但这些措施只能提高炮弹的瞄准精度和目标的跟踪精度。要想从根本上解决打击高机动目标的问题，就必须使小口径高炮弹丸可控，能根据目标的运动来修正弹丸弹道，从而实现对高机动目标的精确打击。

由于小口径高炮弹的弹体空间限制，很多常见的弹丸控制机构无法使用。不仅如此，小口径高炮弹所面对的是高速、快机动目标，其控制机构也必须具备快速改变弹丸速度方向的能力。脉冲发动机由小型雷管组成，可在短时间内产生很大的力，是解决此类问题的有效方法。

使用脉冲发动机对小口径高炮弹的弹道进行修正，必须研究弹丸在脉冲发动机作用下的运动特性，而获得弹道微分方程的解析解则是研究该问题的主要方法。文献[5-7]在复数平面内建立了弹丸的攻角方程并获得了解析解，是所有研究该问题的基础。文献[8-11]在此基础上研究了脉冲作用下的飞行稳定性条件。文献[12-13]建立了脉冲作用下的弹丸复攻角方程，但均未研究脉冲作用与速度偏角之间的关系。Daniel等忽略了脉冲作用的动态过程，直接根据脉冲发动机的冲量估算出由其引起的攻角和攻角角速度，并以此为初始条件分析弹丸的角运动。文献[15-17]通过对弹道方程进行数值积分获取数值解，从而对脉冲修正弹的弹道特性进行分析。这种方法虽然也可以获取一些结论，但是仿真结果与仿真条件之间的关系并不明确，很难为制导控制提供依据和参考。还有一些学者通过采用参数优化设计或者模型预测控制等方法对脉冲修正弹进行点火控制，从而避免了脉冲作用对弹丸运动影响的讨论。然而总结这些研究内容不难发现，这些文献的研究对象均为低马赫数弹箭(如末段修正的火箭弹、迫击炮弹)，它们的速度偏量均由脉冲发动机的直接力提供，气动力的影响都非常小。对于高动态的小口径高炮修正弹，这些点火控制方法很难直接运用。

本文针对小口径高炮修正弹的高动态特性，将脉冲作用分为两个动态过程进行研究。通过建立和求解弹丸复数平面内的攻角方程、偏角方程，量化每个过程对速度方向的影响，分析速度偏角的产生机理，从而为小口径高炮修正弹的总体设计和制导方法优化提供参考。

1 小口径高炮修正弹的工作原理

小口径高炮修正弹以30 mm口径高炮为发射平台，以高炮火控雷达和火控系统为基础，用于提高小口径高炮的射击精度和近程防空能力。当高炮火控雷达探测到目标进入高炮射程后，火控计算机给出发射拦截弹指令。之后火控雷达仍需继续探测目标和拦截弹的位置，并传输给火控计算机。火控计算机对这些数据进行处理，预估拦截弹能否成功拦截目标。当拦截弹无法命中目标，或目标运动方向发生改变时，火控计算机会计算出点火指令(包括点火角度和点火数目)，并通过火控雷达发送给拦截弹。拦截弹收到指令后执行指令，修正弹丸弹道，提高拦截精度。小口径高炮修正弹的工作原理如图1所示。

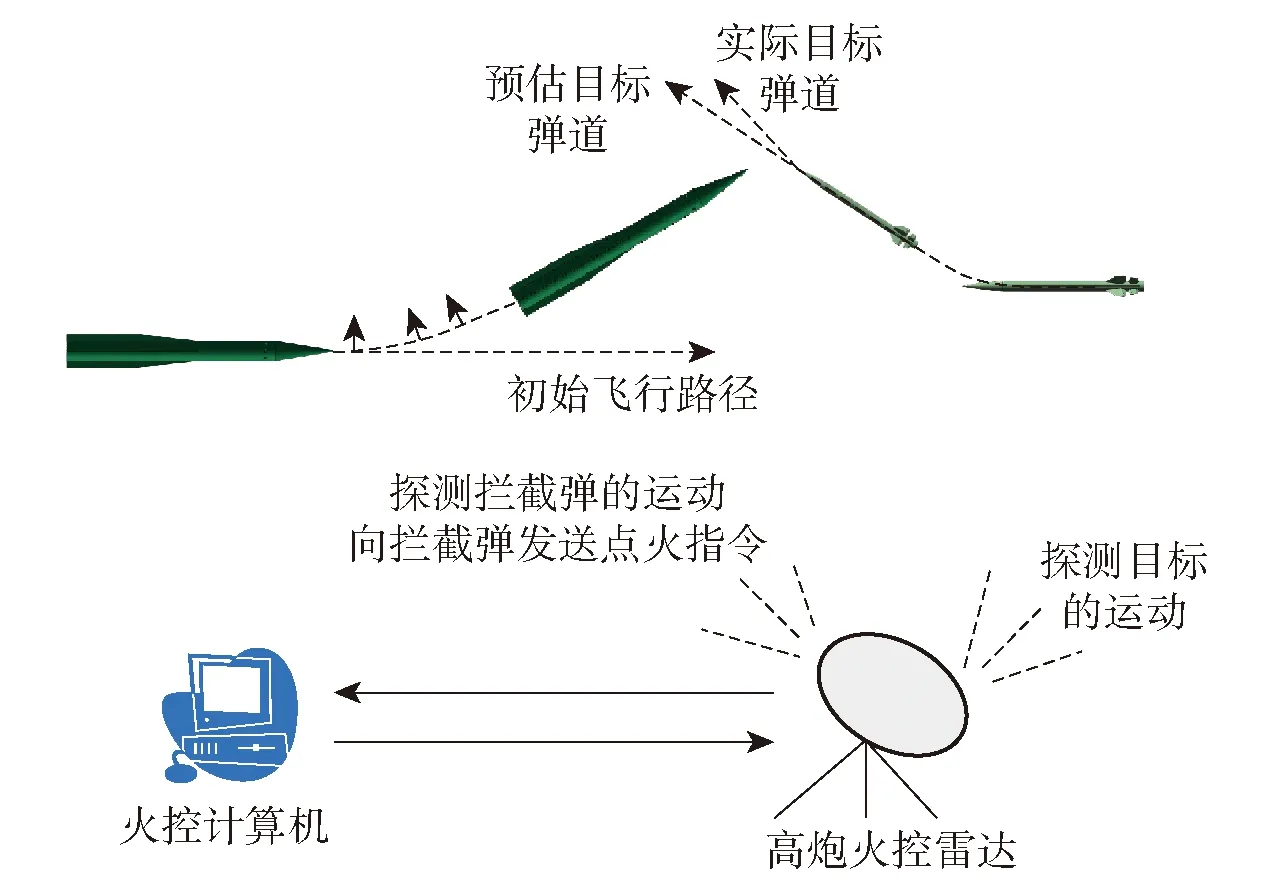
图1 小口径高炮修正弹的工作原理Fig.1 Working principle of correction projectile

由于功能的需要，小口径高炮修正弹由弹体、尾翼、战斗部、弹载计算机、天线和脉冲发动机6部分组成。尾翼通过翼片斜置角使弹丸在飞行过程中保持低速旋转，这样可以实现所有脉冲发动机向一个方向修正，使得修正量达到最大。由于弹丸的自转，脉冲发动机在点火期间并不固定在某个特定的位置上，而是转过了一个扇面，如图2(从弹尾向弹头方向看)所示。

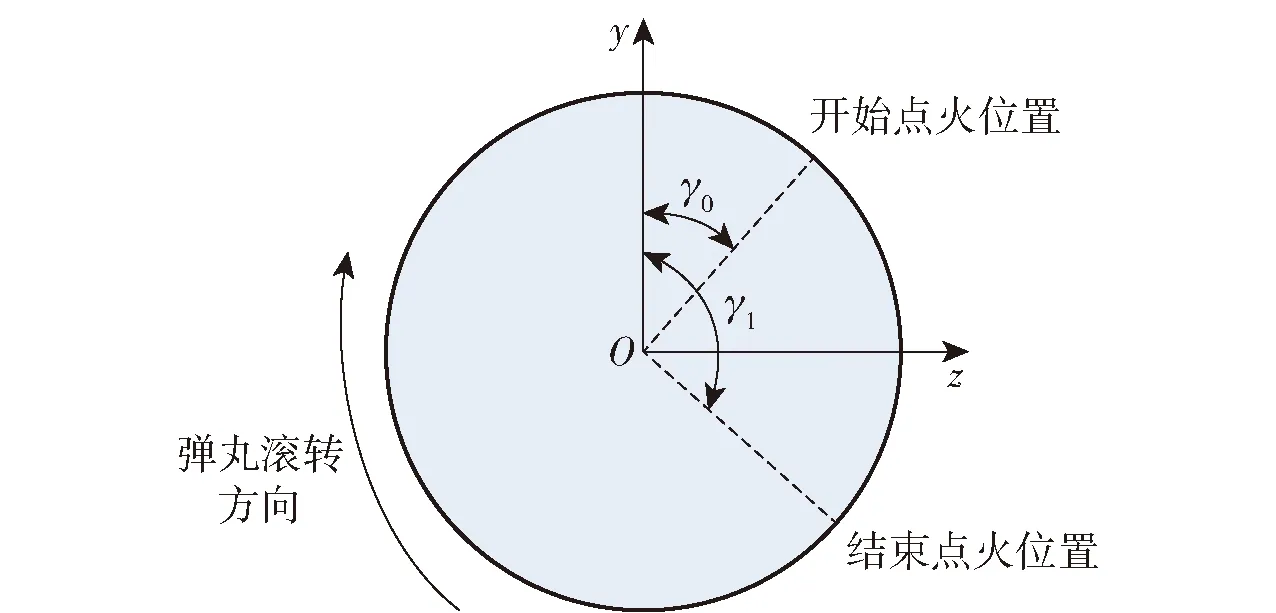
图2 脉冲发动机的工作原理Fig.2 Operating principle of pulse thruster

(1)

2 小口径高炮修正弹角运动方程

2.1 角运动的几何描述

沿着弹丸速度的方向，任选一点′作一个垂直于弹丸速度的平面。速度与该平面的交点定义为原点，弹轴与该平面的交点定义为点。以方向攻角在该平面上的投影为虚轴，高低攻角在该平面上的投影为实轴。这样所建平面即为一个复数平面，如图3所示。图3中，表示攻角平面偏离实轴的角度，顺时针为正，为攻角。

图3 复平面内的攻角Fig.3 Angel of attack in complex plane

因此攻角在该复数平面内可表示为

=+i

(2)

则攻角在该复数平面内还可以表示为

=||ei

(3)

当弹丸的攻角发生变化时，通过点在复数平面内的轨迹可形象反映弹丸弹轴绕速度线变化的过程。文献[5-6]对复数平面内的攻角方程进行了详细阐述，得到了以弧长为自变量的复攻角方程如下：

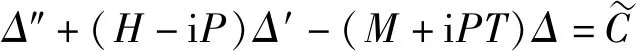
(4)

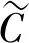
(5)

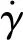
表1 气动力与力矩的复数形式Tab.1 Complex forms of aerodynamics and moment of force

2.2 角运动方程的解

在系数冻结法假设下，攻角方程式是一个2阶非齐次常系数线性微分方程。根据常系数线性微分方程理论可知，方程式的解由齐次解和非齐次解叠加而成，齐次解表示由初始条件引起的运动，而非齐次解表示强迫因素造成的运动。由于脉冲作用随弹体滚转，是一个指数强迫函数，方程式的通解可表示为

=e+i(+)+e+i(+)+ei

(6)

式中：、和分别表示快圆、慢圆和强迫圆的幅值；为弹道弧长；、分别表示快圆、慢圆的初始相位角；、、分别表示快圆、慢圆和强迫圆的角频率，、分别表示快圆和慢圆的阻尼指数，

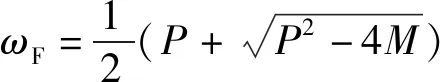
(7)

(8)

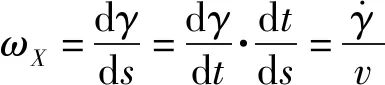
(9)

(10)

(11)

(6)式等号右边的前两项为方程式的齐次解，第3项为方程式的非齐次解。由(6)式可知，在脉冲强迫作用下，弹丸的角运动将是3个圆运动的叠加。

文献[12]指出，脉冲作用下的弹丸角运动可分为两个过程，一是脉冲直接力作用下的弹丸强迫运动，二是在脉冲直接力作用结束后，以第一过程结束时的状态为起始条件由气动力引起的弹丸运动。因此，第一过程的角运动就是方程式的通解，第二过程的角运动是方程式的齐次解。

2.3 脉冲作用在复数平面内的描述

脉冲发动机作用时会对弹丸产生一个脉冲力和力矩。仿照文献[5]中的形式，脉冲力作用在复攻角方程中可表示为

(12)

式中：为脉冲力的大小；为复数域内的弹体转速。

脉冲发动机作用时产生的力矩作用在复攻角方程中可表示为

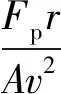
(13)

式中：为脉冲发动机喷口圆心与弹丸质心之间的距离在弹轴上的投影。

同时考虑脉冲作用产生的力和力矩，令

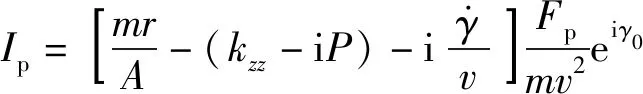
(14)

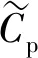
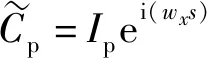
(15)

3 脉冲作用下的弹丸角运动特性

3.1 脉冲直接力产生的强迫角运动

(15)式代入(4)式中，可得

″+(-i)′-(+i)=ei()

(16)

由22节分析可知，(6)式即为(16)式的通解，且(6)式中等号右边的第3项是(16)式的一个特解。将该特解代入(16)式中，化简得

(17)

假设脉冲发动机点火之前弹丸稳定飞行，即=0时有=0°，′=0°m。在该初始条件下，有

(18)

式中：

(19)

解(18)式，得

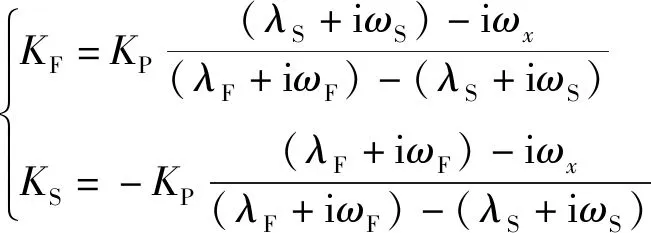
(20)

至此，由脉冲发动机作用所产生的攻角就完全可求，其计算式为

=e+i+e+i+ei

(21)

(21)式对弧长求导，得攻角角速度方程为

′=(+i)e+i+
(+i)e+i+iei

(22)

以某小口径高炮修正弹为例，分别以数值计算方法和解析方法获得其攻角变化过程。为了最大程度地减小重力与脉冲作用的耦合效应，仿真中的等效点火角设为90°。仿真所用弹丸和脉冲发动机参数见表2和表3，仿真结果见图4。

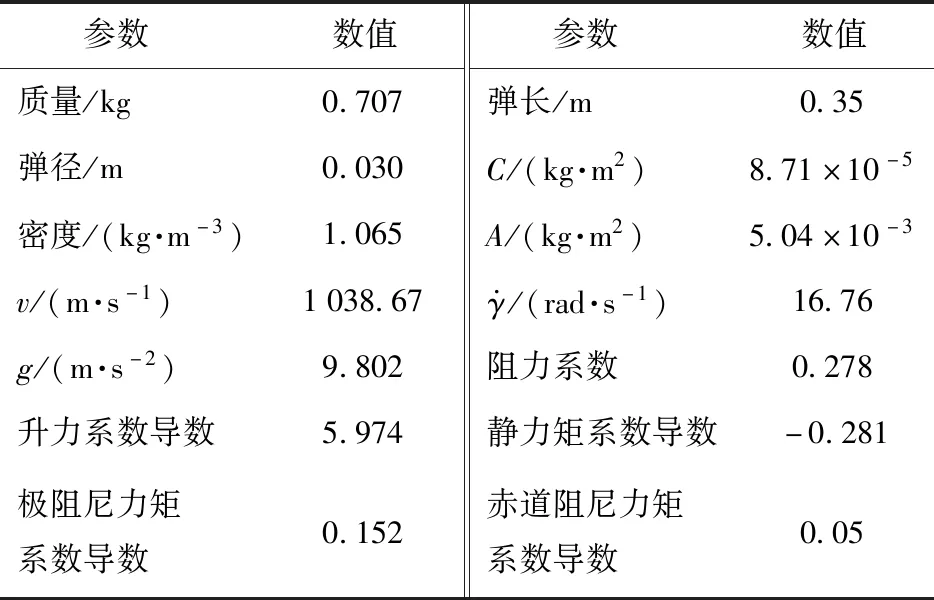
表2 弹丸仿真参数Tab.2 Simulation parameters of projectile

表3 脉冲发动机仿真参数Tab.3 Simulation parameters of pulse thruster

图4中，简化数值解是指仿真所用的6自由度弹道方程中不考虑重力，且数值积分初始时刻为脉冲发动机开始点火时刻；完整数值解是指对完整的6自由度弹道方程进行数值积分获得的解。从图4中可以看出，简化数值解和解析解获得的结果基本一致，而完整数值解和解析解的初始高低攻角有约0002°的差异。由前文分析可知，在使用解析方法求解时，假设弹丸飞行稳定，起始攻角为0°。

图4 脉冲直接力作用下的弹丸攻角Fig.4 Angle of attack of projectile under the action of pulse direct force

在实际情况中，由于动力平衡角的存在，弹丸稳定飞行时的攻角不为0°，故两种方法的初始高低攻角有一个很小的偏差。随着弹道弧长的伸长，两种方法计算的结果偏差量也基本保持不变。表明在脉冲发动机工作的过程中，重力的影响远小于脉冲和气动力的影响。(21)式表示脉冲直接力作用下的弹丸攻角运动应为3圆运动，但由于脉冲发动机作用时间短，无法从图4中看见任何完整的圆运动。

弹轴首先沿着脉冲发动机开始点火时推力的方向离开速度轴，形成负的高低攻角和方向攻角。由于攻角运动是3个圆运动的叠加，之后攻角曲线的形状由3个圆运动的角速度共同决定。此时，强迫圆的角速度为0016 1 rad/m，快圆、慢圆的角速度分别为0008 7 rad/m和-0008 4 rad/m。由图2可知，脉冲发动机绕着轴对称工作，脉冲发动机工作结束后强迫圆的高低攻角应为0°。由于快圆、慢圆的角速度慢于强迫圆，当强迫圆的高低攻角由向负向增大，最后回到0°时，快圆、慢圆的高低攻角始终为负。此外，强迫圆的角速度约为快圆、慢圆角速度的2倍，因此快圆、慢圆转过的角度应为强迫圆的一半，即快圆、慢圆的高低攻角由0°向负向一直增大，且最后保持不变。因此，3个圆运动的叠加形成了图4所示的攻角曲线。

使用文献[14]中的公式计算出由脉冲直接力引起的攻角为0004 68° ，与数值仿真的结果相差很大。表明对于小口径高炮修正弹，虽然脉冲直接力的作用时间极短，但仍是气动力与脉冲力耦合作用的高动态过程，不适合对该过程做相同简化。

3.2 脉冲作用引起的气动角运动

脉冲作用结束后，复攻角方程中不再包含非齐次项，(4)式变换为

″+(-i)′-(+i)=0

(23)

由22节分析可知，(23)式的解只有齐次解，(6)式变为

=e+i+)+e+i(+)

(24)

(24)式中的待定系数和由起始条件确定。文献[5]指出(24)式中的阻尼分量对初始条件影响很小，将(24)式对弧长求导并忽略其中的阻尼分量，得

′=(+i)ei+(+i)ei

(25)

式中：、的定义与(19)式一致。

联立(24)式和(25)式，令=0，即可解出初始攻角、初始攻角角速度′与、之间的关系，如(26)式所示：

(26)

将脉冲直接力引起的起始条件(见(21)式～(22)式)代入(26)式中，即可求得脉冲直接力作用结束后气动力引起弹丸角运动的解析解：

=e+i+e+i

(27)

将31节仿真的结果代入(26)式中进行进一步仿真，结果如图5所示。

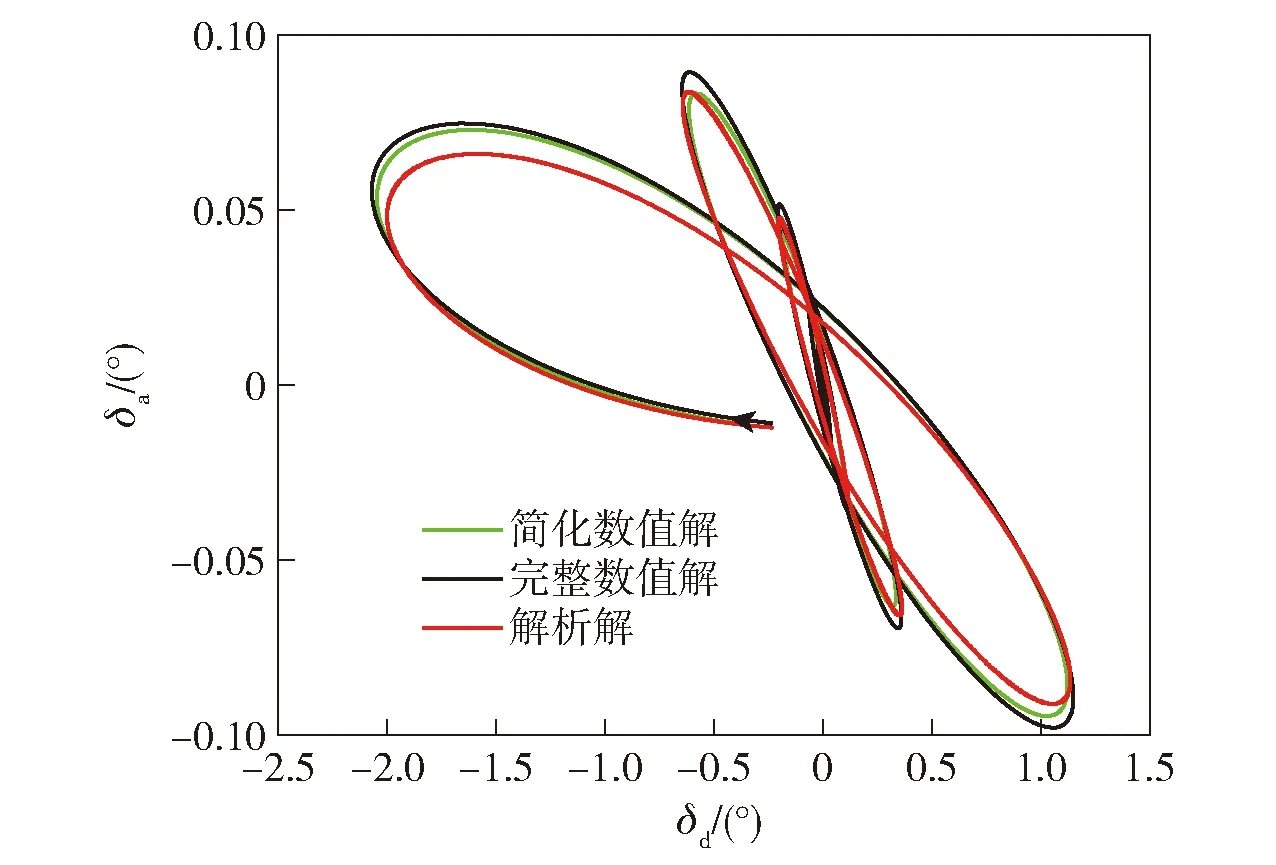
图5 脉冲作用引起的气动力下的弹丸攻角Fig.5 Angle of attack of projectile under the action of aerodynamic force caused by pulse action

从图5中可以看出，在仿真开始的第1个周期内，简化数值解和完整数值解一致性较好，解析解与二者有较大差别。这是因为解析解的初始攻角和初始攻角角速度是由31节给出的。在31节的解析仿真中，积分变量是弹道弧长，因此无法精确计算仿真的终止条件(数值仿真时是以时间为积分变量，且脉冲发动机工作时长已知，因此能进行精确仿真)。虽然在31节的仿真末段中，攻角的变化已趋于平缓且与简化数值解一致，但是该段攻角角速度变化剧烈，代入(26)式中的值与数值仿真存在差异，故在本节仿真初始段，解析解和两种数值解存在差异。由(26)式可知，该误差只存在于快圆、慢圆的幅值中，对二圆运动的角速度和阻尼系数均无影响，因此图5中3种结果的角运动频率基本一致，且都在做幅值不断减小的圆运动。

随着弹道弧长的伸长，阻尼作用开始显现。由初始攻角角速度带来的误差影响慢慢减弱，因此简化数值解和解析解之间的差异越来越小。与此同时，完整数值解中的重力影响逐渐显现，故两种数值解之间的差异逐渐增大。这些现象在图5中均有体现。从图4和图5的仿真结果可以看出，解析解具有较高的精度。

4 脉冲作用对速度方向的影响

攻角运动方程描述了弹轴相对于速度线的运动。脉冲发动机作用时和作用后都会产生攻角，有了攻角就会在攻角面内产生升力。由于弹丸的自转，攻角面会不断地绕速度线旋转，升力的方向也在不断变化，于是速度方向也在不断旋转改变。对于脉冲直接力—气动力复合修正方法，分析清楚两种作用效果对速度方向的改变更为重要。

4.1 脉冲直接力对速度方向的影响

与攻角方程类似，描述弹丸速度方向变化的方程是复偏角方程，复偏角的定义如下

=+i

(28)

式中：为复偏角；为速度高低角增量，称为高低偏角；为速度方向角增量，称为方向偏角。

由于弹丸低速旋转，马格努斯力相比于升力很小，可忽略。只考虑弹丸升力和脉冲作用力的复偏角导数方程为

(29)

将31节中脉冲作用产生的攻角代入(29)式中，

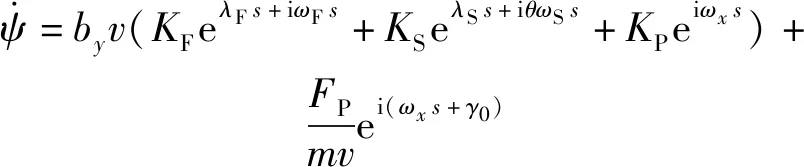
(30)

将(30)式中的自变量由弧长换成，并对求积分，得

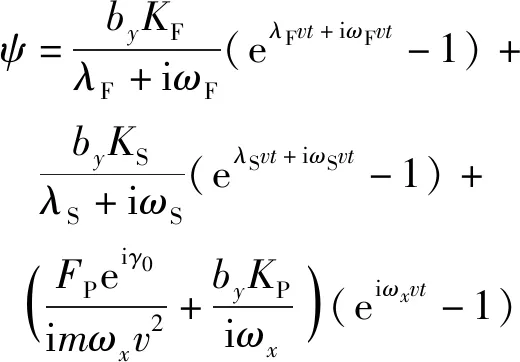
(31)

由(31)式可知，在脉冲作用下，弹道偏角也遵循三圆运动规律。选择与31节相同的条件进行仿真，仿真结果见图6。

图6 脉冲直接力作用下的弹丸偏角Fig.6 Deflection angle of projectile under the action of pulse direct force

从图6中可以看出，简化数值解和解析解的计算结果基本相同，完整数值解的方向偏角与前二者相同，高低偏角差异较大，这仍是由重力引起的。

从图6中还可以看出，脉冲发动机作用后，弹丸沿推力方向上有一个速度增量，产生一个偏角，在垂直于推力方向上也会有一个偏角，仿真值为-0001 12°。由于脉冲发动机作用时间短，故垂直于推力方向的偏角很小，可忽略。

4.2 脉冲引起的气动角运动对速度方向的影响

(29)式是包含了升力和脉冲作用力的复偏角导数方程，当脉冲作用结束后，(29)式则改写为

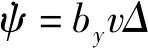
(32)

将32节中脉冲作用结束后气动力作用下的攻角方程代入(32)式中，得

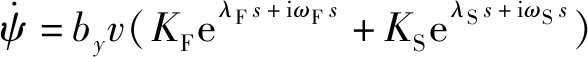
(33)

同样，将(33)式中的自变量由弧长换成，并对求积分，得

(34)

(35)

继续选用31节中的条件进行仿真，结果如图7和图8所示。

图7 脉冲作用引起的气动力下的弹丸方向偏角Fig.7 Direction deflection angle of projectile under the action of aerodynamic force caused by pulse action

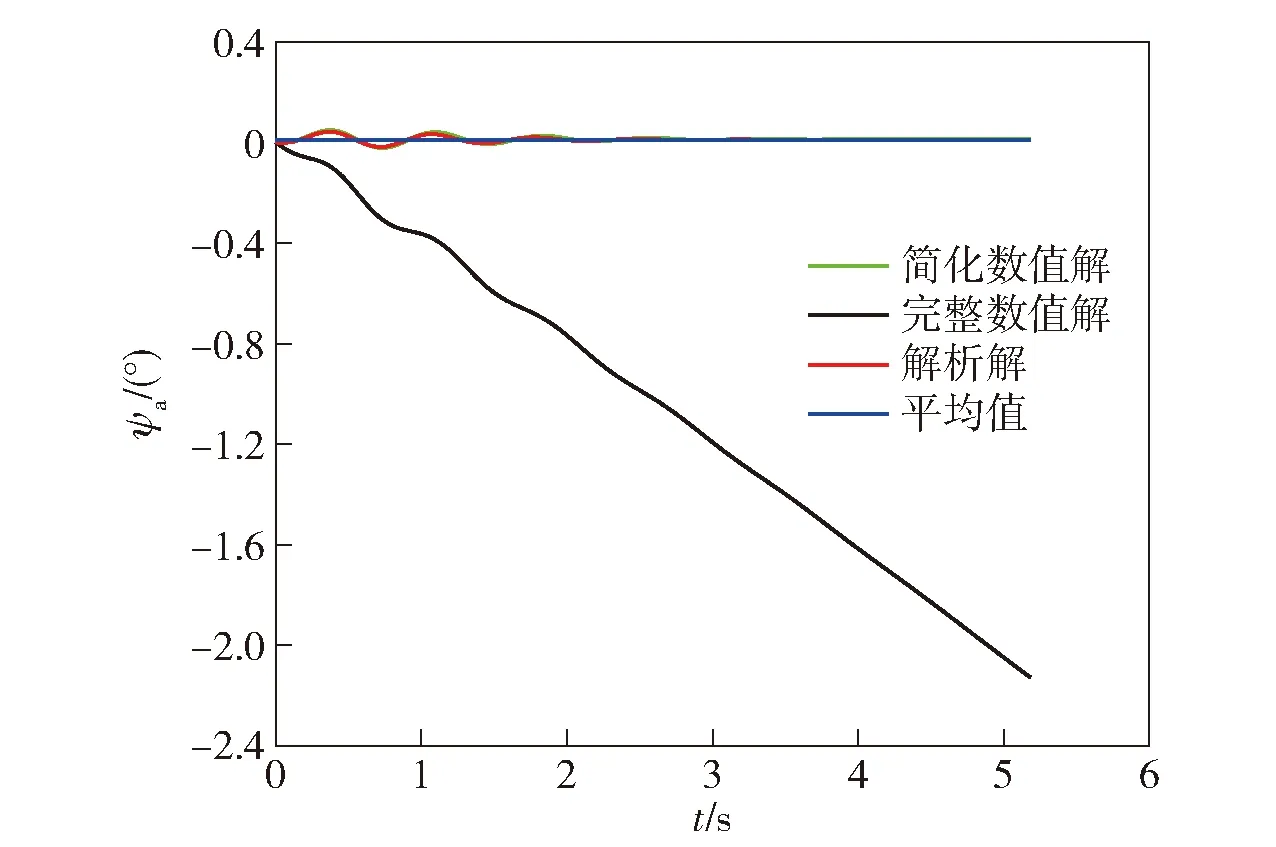
图8 脉冲作用引起的气动力下的弹丸高低偏角Fig.8 Height deflection angle of projectile under the action of aerodynamic force caused by pulse action

从图7和图8中可以看出，解析解得到的高低偏角和方向偏角均收敛于对应的偏角平均值，从而验证了理论分析的正确性。气动力产生的偏角为0976°，而脉冲直接力产生的偏角为0009 7°，前者是后者的100倍。从图8可以看出，气动力作用在垂直脉冲发动机推力方向上产生的速度偏角已较大(仿真值为0011 2°)，在进行远距离修正或多个脉冲发动机修正时，制导控制系统需考虑该值的影响。

4.3 速度偏角的产生机理

小口径高炮修正弹是通过脉冲发动机和气动力的共同作用使弹丸的速度方向发生改变，从而达到修正的目的。在脉冲发动机作用期间，速度偏角就是由于脉冲发动机的推力而产生的。由42节分析可知，气动力产生的偏角是由攻角计算得到的。因此将42节中仿真的弹丸方向攻角和方向偏角曲线绘制在一幅图中，如图9所示，将42节中仿真的弹丸高低攻角和高低偏角曲线绘制在一幅图中，如图10所示。

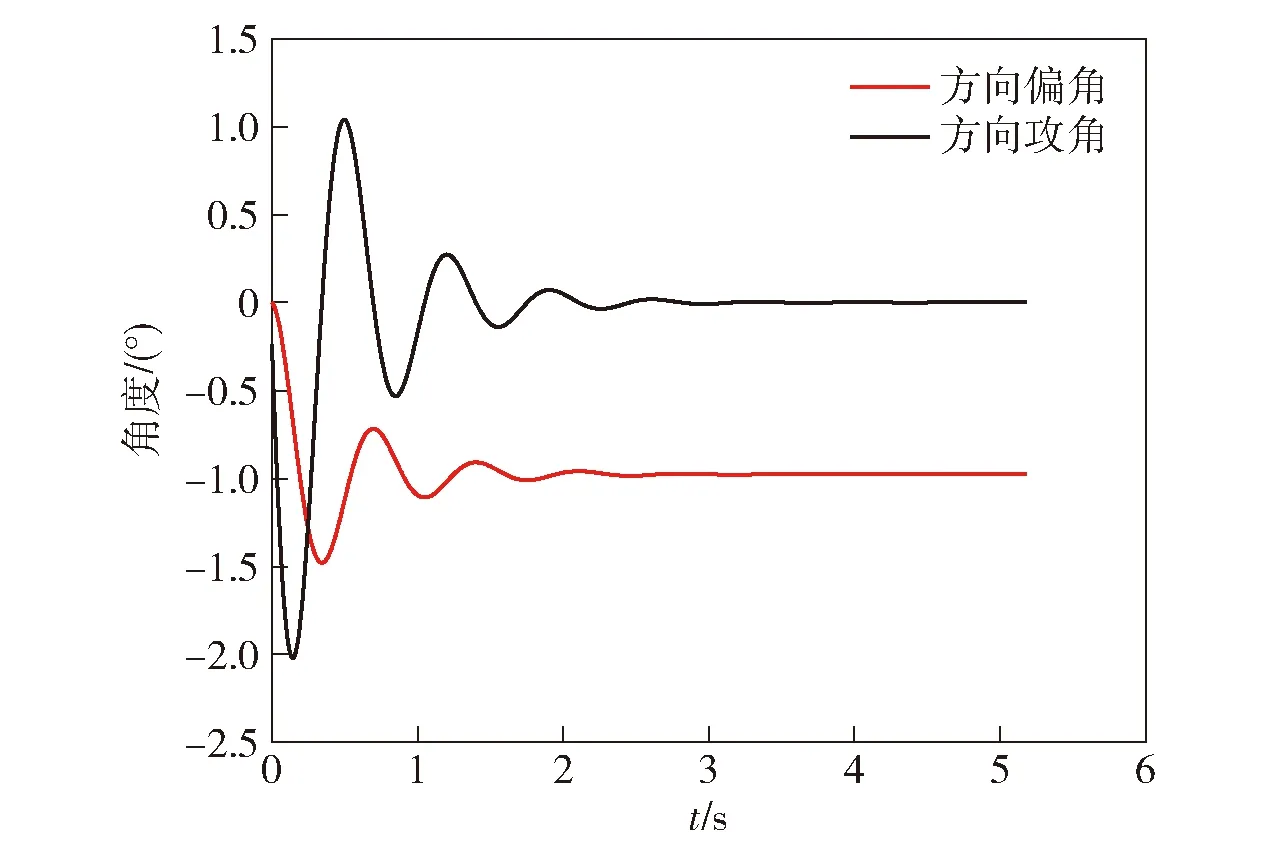
图9 弹丸的方向攻角和方向偏角Fig.9 Directional angle of attack and directional deflection angle of projectile

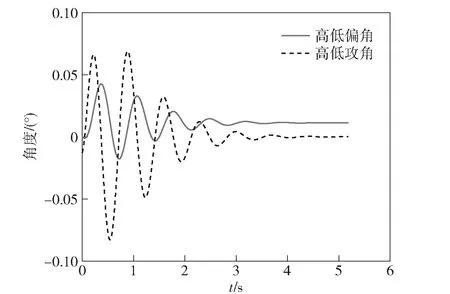
图10 弹丸的高低攻角和高低偏角Fig.10 Height angle of attack and height deflection angle of projectile

由图9、图10可以看出，当攻角为负时，偏角负向增大；当攻角为正时，偏角正向增大。由于阻尼的存在，平均偏角的正负将由初始攻角和初始攻角角速度的正负决定。

由31节的分析可知：虽然脉冲发动机在等效点火角两侧对称工作，但这只能保证强迫圆运动在垂直于推力方向上的作用相互抵消，而快圆、慢圆运动在垂直于推力方向上会产生攻角和角速度。由图4可知，在脉冲发动机点火期间，弹丸的高低攻角一直为负。该负攻角使偏角负向增大，即图6中的高低偏角从0°一直减小到-0001 12°。脉冲直接力作用结束后，在垂直于推力方向上的攻角角速度亦不为0 rad/s，之后该方向上的攻角作幅值不断减小的摆动运动，最后形成的平均偏角为0011 2°，如图10所示。由此可见，脉冲直接力和脉冲引起的气动力在垂直于推力方向上所产生的速度增量方向相反，且后者约为前者的10倍。

为了使单个脉冲发动机产生的速度修正量达到最大，则必须使脉冲直接力和气动力产生相同方向的速度修正。对于尾翼稳定弹丸，如果脉冲发动机安装在质心之前(更靠近于弹头方向)，则其产生的速度偏角沿发动机推力方向，产生的攻角和角速度也是沿该方向，此时脉冲直接力和气动力的作用是叠加的；如果脉冲发动机安装在质心之后(更靠近于弹尾方向)，则其产生的速度偏角仍沿发动机推力方向，但是其产生的攻角和角速度方向则是推力的反方向，这时脉冲直接力和气动力的作用是相抵消的。由42节分析可知，气动力对速度方向的影响远大于脉冲直接力，因此将脉冲发动机安装在尾翼弹质心之后，修正方向与脉冲发动机推力方向相反，且修正的偏角绝对值偏小。