当量比对煤油- 空气两相旋转爆轰波的影响

冯文康，郑权，汪小卫，董晓琳，翁春生，肖强，孟豪龙

(1.南京理工大学 瞬态物理国家重点实验室，江苏 南京 210094；2.中国运载火箭技术研究院，北京 100076)

0 引言

旋转爆轰推进系统是极具发展潜力的一种新型推进系统，相比于传统的等压燃烧，爆轰循环热效率可提高20%～50%，且具有易于点火、进气速度范围大、低压比下有效推力大、结构简单等优点，近年来引起了国内外学者的广泛关注。

国外方面，Bykovskii等用氢气、乙炔、丙烷、煤油等多种燃料进行了旋转爆轰实验，实现了氢气- 空气旋转爆轰。实验过程中发现，当以丙烷或煤油作为燃料时，必须向空气中添加额外的氧气(50%N，50%O)才能实现旋转爆轰。Kindracki通过向液态煤油- 空气混合物中加入少量氢气实现了两相旋转爆轰，爆轰波速具有20%～25%的亏损。Frolov等进行了氢气- 液态丙烷- 空气旋转爆轰实验，在丙烷和空气流量不变、氢气流量迅速下降的情况下，旋转爆轰波持续了约0.1 s。Gaillard等采用不同的燃料喷注方式开展了氢气- 氧气旋转爆轰波的数值模拟研究，发现在非预混喷注条件下，燃料和氧化剂的掺混效果差，出现推进剂分层现象，仅有不到20%的推进剂参与了爆轰燃烧。Prakash等开展了甲烷- 氧气旋转爆轰波的数值模拟研究，发现爆轰波的强度在空间上是波动的。Zhao等采用燃料与氧化剂分开喷注的方式进行了氢气- 空气旋转爆轰波的数值模拟研究，发现波前燃料与氧化剂掺混极不均匀，参与爆轰燃烧的氢气有70%以上是在贫燃条件下被消耗的。Hayashi等开发了欧拉- 欧拉两相控制方程求解程序，对煤油(JP-10)- 空气两相旋转爆轰波进行了数值模拟，发现JP-10的预蒸发程度越高，越有利于爆轰波的传播。

国内方面，北京大学、清华大学、国防科技大学、南京理工大学、哈尔滨工程大学、空军工程大学、西安航天动力研究所等多家单位对旋转爆轰波开展了大量实验和数值模拟研究，目前的研究以气态燃料为主，液态燃料的研究仅开展了一小部分。实验方面，王迪等采用富氧空气或氧气为氧化剂开展了两相旋转爆轰实验，发现随着氧化剂中氧气与氮气比例的增加，爆轰波速逐渐增大。李宝星等、Zheng等、郑权等开展了大量煤油- 富氧空气旋转爆轰实验，研究了两相旋转爆轰波的起爆过程、传播特性和传播不稳定性等特征。葛高杨等实验验证了以高总温空气为氧化剂、汽油为燃料的旋转爆轰发动机长时间连续稳定工作的可行性，获得的旋转爆震波传播频率为1 907.5 Hz。Zhong等通过将煤油预燃烧裂解的方法实现了煤油- 富氧空气旋转爆轰，研究了氧含量(30%和50%)对爆轰波的影响。胡洪波等开展了煤油富燃燃气旋转爆轰实验，发现与液体煤油相比，煤油富燃燃气能够在更低氧含量的富氧空气中实现旋转爆震波的稳定传播。Liu等采用间隔喷注方式研究了预混条件下煤油- 空气旋转爆轰波的传播特性，发现在远离入口位置存在爆燃区，大面积爆燃使流场发生畸变，影响了燃烧室工作性能。李宝星等进行了汽油- 富氧空气旋转波的爆轰数值模拟，结果表明爆轰波的传播频率为4 390 Hz，平均推力约为880 N。王丹等开展了部分裂解煤油的旋转爆轰波数值模拟，结果表明煤油裂解率20%以下时，改变裂解率对发动机稳定工作后的性能无明显影响。

从现有的研究来看，实现煤油等常见液态燃料的旋转爆轰较为困难，一般需要添加额外的氧气或氢气等活性成分。尽管液态燃料旋转爆轰实现的条件更为苛刻，但由于液态燃料具有易于存储、热值高等特点，从实际工程应用的角度来看，液态燃料的使用是势在必行的。但是，目前气- 液两相旋转爆轰波的研究十分欠缺，尤其在数值模拟方面，大多数值模拟在将液态燃料视为蒸气并与氧化剂充分混合的条件下开展，与实际情况存在较大差异。

基于以上考虑，本文基于欧拉- 拉格朗日方法对常温液态煤油- 高总温空气两相旋转爆轰波进行了二维数值模拟，采用ANSYS Fluent求解器求解可压缩理想气体的非定常有黏化学反应流动控制方程和液滴运动控制方程，研究了当量比对两相旋转爆轰波传播特性的影响。

本文在将液滴喷注点间隔布置于来流中的条件下对两相旋转爆轰波进行了数值模拟，计算条件更接近于实际情况。文中分析了两相旋转爆轰流场中燃料的分布特性，加深了对两相旋转爆轰流场结构的认识；分析了当量比对两相旋转爆轰波波头高度、爆轰参数、速度亏损和推力性能的影响规律。本文研究有利于更好地理解两相旋转爆轰波的传播过程，可为实验观测结果提供理论依据。

1 数理模型

1.1 物理模型

旋转爆轰燃烧室通常采用同轴环腔式结构，现有大多数关于旋转爆轰波的数值研究都采用施加周期性边界条件的方法，对环形燃烧室周向中心切面上爆轰波的传播特性展开二维模拟，本文也采用该方法。如图1所示，其中为二维笛卡尔坐标系原点，表示周向方向，表示轴向方向。计算域尺寸为300 mm×90 mm，下方为入口，上方为出口，左右两侧为周期边界。在入口处等间距地布置60个燃料喷注点，各燃料喷注点之间的间距为5 mm，液滴以源项加质的方式从各喷注点进入计算域，液滴的初始粒径为002 mm，计算采用的网格尺寸为05 mm×05 mm。

图1 物理模型Fig.1 Physical model

1.2 数学模型

121 气相控制方程

以笛卡尔张量形式表示的黏性可压缩理想气体非稳态雷诺平均控制方程如下：

(1)

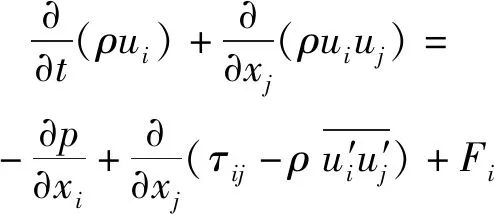
(2)

(3)

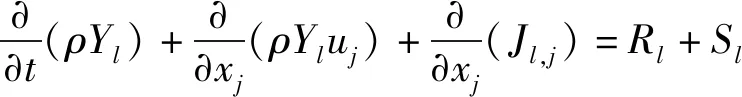
(4)

=

(5)

式中：、、、、、、、、，、、分别表示位置、时间、密度、压力、温度、速度矢量、总能、组分的质量分数、组分的扩散通量分量、传热系数和气体常数；为黏性应力张量，下标，∈{1，2}，表示方向分量；′为脉动速度分量；、、、、和均为源项，为液滴的蒸发速率，为第方向液滴受到的流体曳力的分量，为化学反应放热量，为液滴蒸发吸收的热量，为组分的蒸发速率，为组分的化学反应净生成率。

湍流项采用标准-模型求解：

(6)

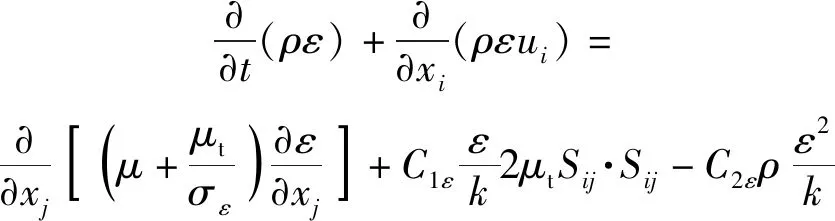
(7)

式中：为气体分子黏度；为平均速度应变率张量；为涡黏度，由湍动动能和黏性耗散率确定，

(8)

、1、2、、均为模型常数，

=009,1=144,2=192,=10,=13

(9)

参与化学反应的反应物为煤油和空气，煤油的分子式取为CH，化学反应为单步反应，反应式如下：

CH+17.75(O+3.76N)=
12CO+11.5HO+66.74N

(10)

组分的化学反应净生成率的计算式为

(11)

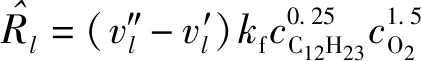
(12)

″为生成物中组分的化学计量系数，′为反应物中组分的化学计量系数，CH和O分别为CH和O的摩尔浓度，为反应速率常数，

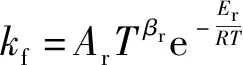
(13)

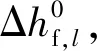
(14)

122 液相控制方程

液滴运动的控制方程如下：

(15)

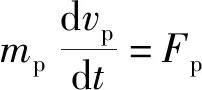
(16)

(17)

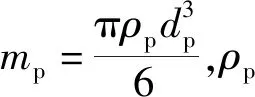
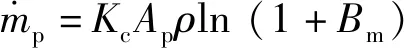
(18)

为液滴表面积，为传质系数，

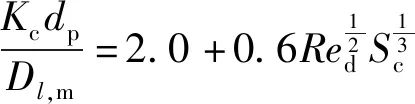
(19)

,m为扩散系数，为Schmidt数，

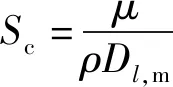
(20)

为中间变量，

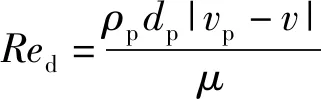
(21)

为气体的速度，为Spalding质量数，

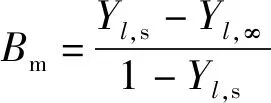
(22)

，s和，∞分别为液滴表面蒸气的质量分数和周围气体中蒸气的质量分数；为作用于液滴的流体曳力，

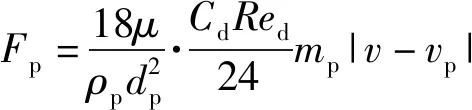
(23)

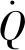
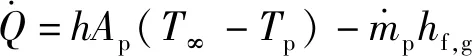
(24)

为气相温度，为潜热，为传热系数，由(25)式计算：

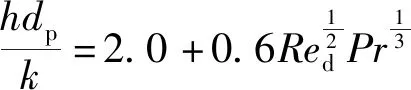
(25)

为气体的普朗特数。

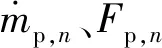
(26)

(27)

(28)

(29)

2 计算方法、定解条件和模型验证

2.1 计算方法

基于ANSYS Fluent计算软件，采用密度基隐式求解器求解12节中的非稳态雷诺平均控制方程，湍流模型为标准-模型，化学反应模型采用有限速率模型，对流项采用3阶逆风单调守恒格式进行离散，物理通量采用迎风型矢通量分解方法进行分解，时间推进采用1阶隐式格式。

液滴的运动采用离散相模型求解，该模型基于欧拉- 拉格朗日方法，连续相的运动通过Navier-Stokes(N-S)方程求解，离散相则通过追踪粒子的运动轨迹求解。液滴在运动过程中会发生破碎，液滴的破碎过程采用Wave破碎模型模拟，该模型认为液滴的破碎是由气- 液两相之间的相对速度引起的。另外，液滴的湍流扩散采用随机游走(DRW)模型模拟，该模型通过随机产生的瞬时湍流速度波动模拟湍流对液滴运动轨迹的影响。

2.2 气相边界条件

入口气体为高总温空气，总温=860 K，总压=06 MPa，入口处的流动被视为等熵流动，入口参数(压力、温度、速度)根据相邻单元的压力和温度确定，有如下3种情况：

1)≥，入口不进气：

=,=,=0 m/s

(30)

2)>>，气流以亚音速进入计算域：

(31)

3)≤，气流以音速进入计算域：

(32)

式中：为比热比；和分别为临界温度和临界压力，

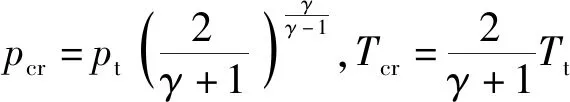
(33)

出口分为两种情况：当出口为亚声速流动时，出口参数由(34)式确定，其中，为与出口边界相邻的流体单元的流动参数，为无穷远处的流动参数，这里取无穷远处为常温常压状态；当出口为超声速流动时=。两个周期边界处的流体单元被视为是相邻的。

=095+005

(34)

2.3 液相边界条件

液滴和空气以非预混的方式进入计算域，空气从入口边界进入计算域，液滴则以源项加质的方式从各喷注点进入计算域。液滴离开喷注点时的初始温度为300 K，初始速度为40 m/s，每个喷注点在时间步长Δ内喷注的液滴数量由(35)式确定：

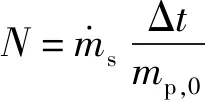
(35)

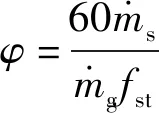
(36)

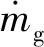
在入口对液滴使用反射边界条件，即当液滴运动到入口时，令其法向动量方向与原方向相反；出口为逃逸边界条件，即当液滴运动到出口时，认为液滴从出口逃逸，运动轨迹计算终止。

2.4 初始条件

计算旋转爆轰流场之前，先计算得到稳定的冷态流场，如图2所示，此时流场各处的流动参数已稳定，以该流场作为初始时刻的流场，并在左侧矩形标记的区域内设置一高温高压区域(=2 MPa，=3 000 K)模拟点火，文献[18，25]中也采用了类似的起爆方式。

图2 初始流场Fig.2 Initial flow field

2.5 模型验证

为验证本文计算方法的准确性，首先，将本文计算得到的旋转爆轰流场和Bykovskii等实验中拍摄的照片进行了对比，如图3所示，其中，为爆轰波，为斜激波，为滑移线，为接触面，为新鲜燃料填充区，计算结果符合典型的旋转爆轰流场特征，与文献[4]实验观测结果定性一致。其次，在=1的计算条件下，流场稳定后爆轰波前的温度和压力分别约为=035 MPa，=700 K，在该条件下使用NASA化学平衡计算软件(CEA)计算的气相理论爆轰参数如表1所示。由表1可见：数值模拟结果与C-J理论值相比，爆轰压力、温度、波速的相对误差分别为-17、34和-122，产生误差的原因可能是由于本文采用的两相、非预混计算条件以及计算时燃料具体成分的差异导致的；数值模拟结果还表明爆轰波速具有较大的亏损，与实验结果中获得的经验一致，本文将对此作进一步讨论。由于本文重点关注旋转爆轰流场的整体流动特性，而非爆轰波阵面的精细结构，计算结果的数值精度是可接受的，因此本文认为采用的计算方法是可靠的。

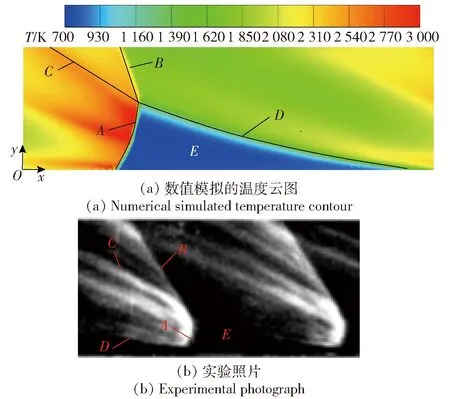
图3 数值模拟与实验观测的流场结构对比Fig.3 Comparison of simulated and experimental flow field structures

表1 数值模拟结果与C-J理论值对比Tab.1 Comparison of C-J theoretical and numerical results

为验证网格无关性，在=1的计算条件下，分别使用网格尺寸为03 mm、05 mm和07 mm的网格进行计算，计算得到的温度云图如图4(a)所示，在=162 ms时刻沿=30 mm处的压力分布如图4(b)所示，通过对比可以发现，3种不同网格尺寸获得的计算结果差异很小，因此本文数值研究将采用05 mm的网格开展。

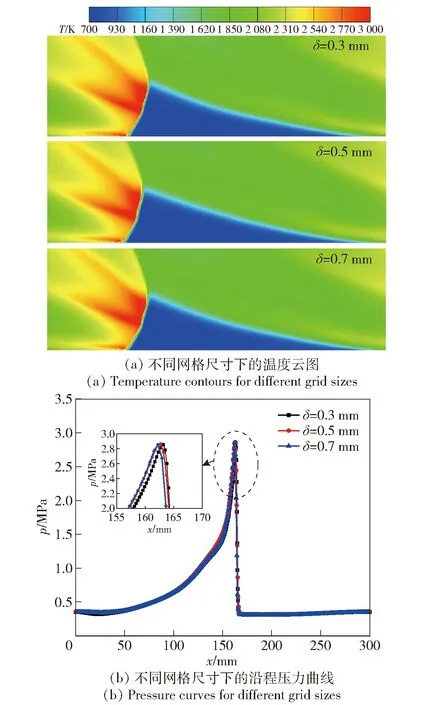
图4 网格无关性验证Fig.4 Grid independence verification

3 结果分析

当量比是影响旋转爆轰流场的关键参数，本文在∈(05，20)的范围内选取若干工况点进行数值模拟，以研究当量比对常温液态煤油- 高总温空气两相旋转爆轰波的影响，不同当量比下爆轰参数的计算结果列于表2中。下面主要从流场结构、传播特性和推力性能3个方面展开讨论。

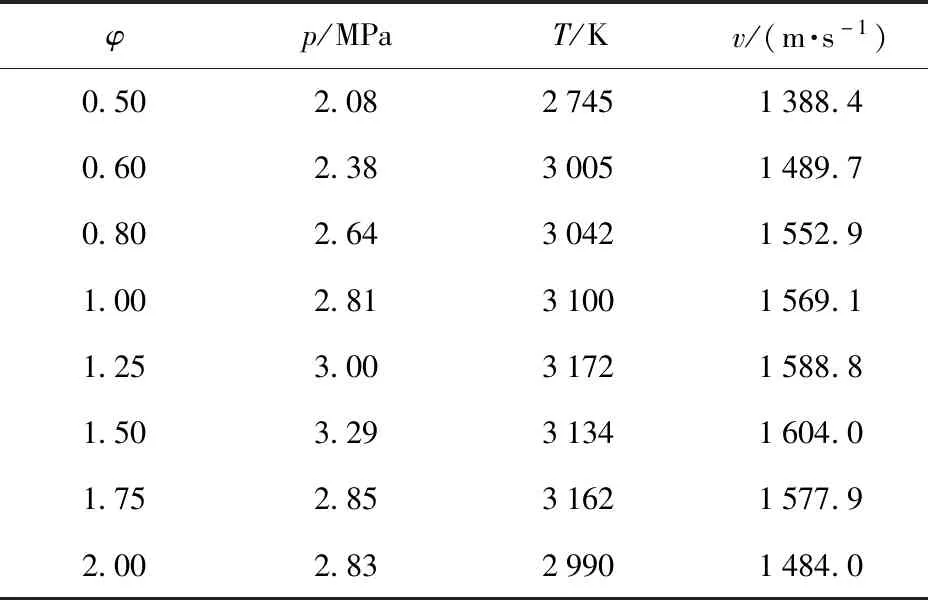
表2 不同当量比下的数值计算结果Tab.2 Numerical results under different equivalent ratios

3.1 流场结构

3.1.1 流场基本特征

爆轰波稳定传播时，常温液态煤油- 高总温空气两相旋转爆轰流场的典型结构如图5所示(=1，=3.29 ms)，该流场结构与气相旋转爆轰流场具有类似的特征，包括爆轰波、斜激波、接触面、滑移线等，如图5(a)所示。压力云图(见图5(b))中显示了部分流线，可以直观地反映不同位置处流体的运动趋势：随着波后压力迅速衰减，燃烧产物加速膨胀产生-轴方向的速度分量，导致波后流线逐渐向-轴方向倾斜。此外，与气相旋转爆轰波相比，可以发现煤油- 空气两相旋转爆轰波波头发生明显倾斜，在温度云图中还可以观察到波后燃烧产物温度分布不均匀，存在局部高温区，下面对这些差异的成因作进一步讨论。图5中，、和3个区域的高度分别为=23 mm、=16 mm、=17 mm，爆轰波头高度=++=56 mm。

图5 流场结构云图Fig.5 Contours of flow field structure

煤油蒸气和氧气的质量分数云图如图5(c)和图5(d)所示，在煤油蒸气质量分数云图中存在2个富燃区域，同时在氧气质量分数云图中存在2个富氧区域，由反应热云图(见图5(e))可知，爆轰波后富燃区域的部分燃料和富氧区域的部分氧化剂接触后继续燃烧，对应温度云图中爆轰波后方高温区域。尽管进入燃烧室的煤油和空气为化学恰当比，由于混合不均匀，一部分煤油和空气并没有发生化学反应，而是随着燃烧产物侧向膨胀排出了燃烧室，出口处煤油蒸气和氧气的质量分数分布如图6所示，煤油蒸气主要集中在∈(0，15 mm)和∈(215 mm，300 mm)范围内，氧气主要集中在∈(15 mm，215 mm)范围内，在=65 mm附近(虚线圆标记的位置)氧气质量分数曲线出现微小下降，这是爆轰波后未耗尽的氧气和新喷注的煤油接触后继续燃烧而被消耗所导致的，对应图5(d)中虚线框内的区域，由图5(a)可见，爆轰波后接触区对应更高的温度。

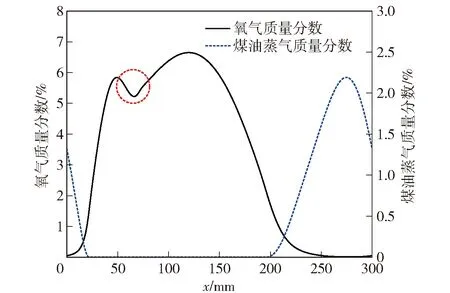
图6 出口处煤油蒸气和氧气的质量分数分布Fig.6 Mass fraction distribution of C12H23(g) and O2 at outlet

3.1.2 液滴分布及当量比的影响

新鲜反应物层的温度云图和液滴粒径分布云图如图5(f)和图5(g)所示，此时爆轰波最前缘位置位于=87 mm处，沿直线=87 mm液滴体积分数和煤油蒸气质量分数的变化如图7所示，根据液滴分布特点，新鲜反应物层可分为3个区域：区域内液滴体积分数为0，不存在未蒸发的液滴，区域内距区域上边界的距离越小、煤油蒸气质量分数越大，区域内液滴体积分数大于0，大量未蒸发的液滴淤积于此，同时煤油蒸气质量分数最大值也出现在区域；区域内部分液滴完全蒸发，在靠近喷注点位置处存在部分未完全蒸发的液滴。、和3个区域的高度分别为=23 mm、=16 mm、=17 mm，爆轰波头高度=++=56 mm。反应物与燃烧产物的接触面位于内，由反应热云图(见图5(e))可知，接触面上发生爆燃，导致内温度迅速升高(见图5(f))，爆轰波扫过前内部分燃料已被消耗。

图7 沿直线x=87 mm的燃料分布Fig.7 Fuel distribution along the line x=87 mm

新鲜反应物层内液滴沿轴方向的不均匀分布是由空气与液滴的速度差异导致的，入口处空气的速度分布如图8所示，在爆轰波后方约50 mm范围内进气速度为0 m/s，液滴沿轴方向的运动受阻，大量液滴淤积在入口附近；随着爆轰燃烧产物侧向膨胀，波后压力逐渐恢复，进气速度迅速增加至数百米每秒，远大于液滴的初始速度，入口处淤积的大量液滴在流体曳力的作用下加速运动，这部分液滴对应于区域(见图5(g))，在一个爆轰波传播周期内，区内的液滴不能完全蒸发，直至下一个周期的爆轰波扫过，从煤油质量分数云图(见图5(c))中可以看出爆轰波扫过区后产生大量煤油蒸气，形成波后的富燃区。由于空气运动速度快，新鲜反应物层内空气到达的高度高于区，运动高度高于区的空气携带区部分已蒸发的煤油，形成区，同时在区下方的局部区域，随着进气速度增加，空气流量增大，进油量与进气量之比已低于化学恰当比(见图5(c))，形成区。在区内，距入口越远，煤油蒸气质量分数越大，分布也更加均匀，如图9所示，在靠近燃烧室入口的位置(=5 mm)，液滴蒸发量小，煤油蒸气的质量分数较低，同时煤油蒸气的质量分数存在较大波动，煤油蒸气与空气混合不均匀，导致化学反应速率降低，爆轰波强度较弱，因此靠近入口位置的反应区滞后，爆轰波波头发生倾斜(见图5)。

图8 入口处y轴方向的速度分布Fig.8 velocity distribution in y direction at inlet

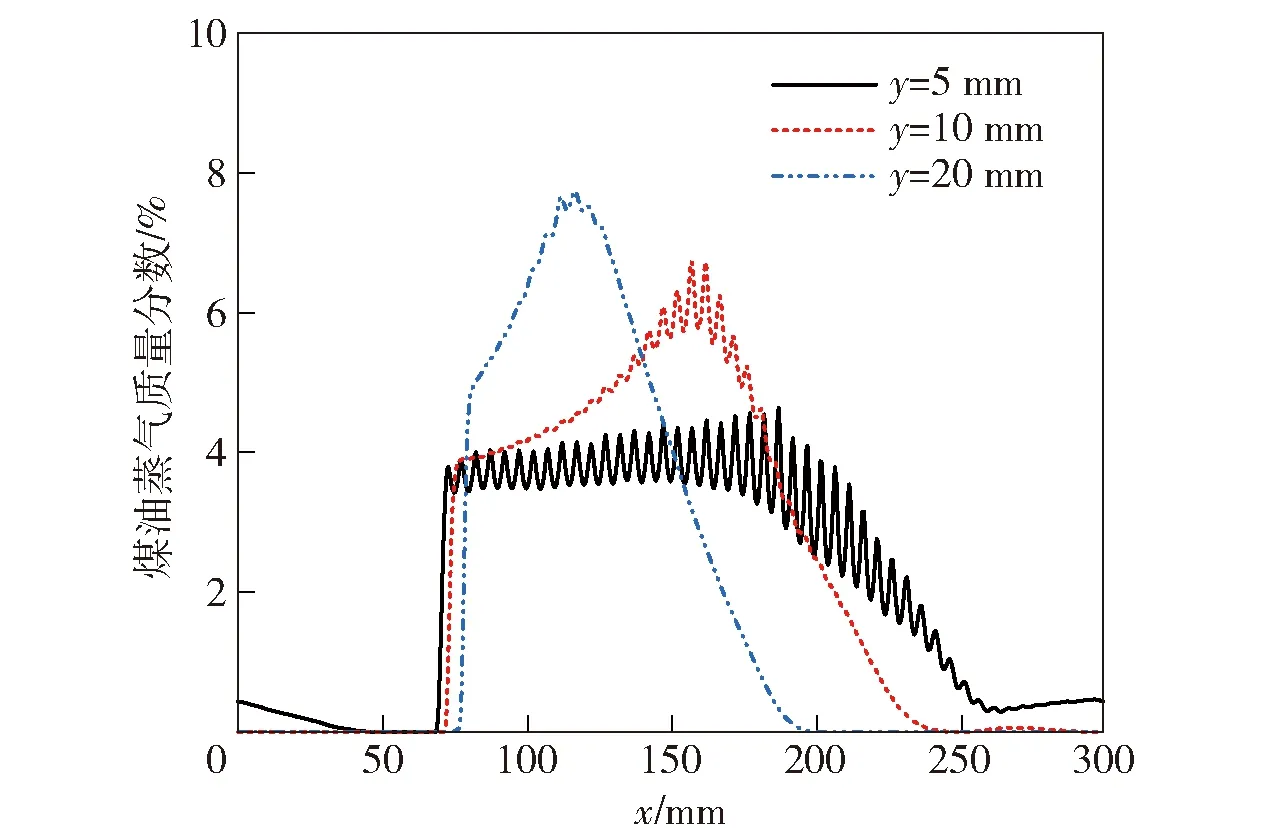
图9 沿x轴方向的煤油蒸气质量分数分布Fig.9 Mass fraction distribution of C12H23 (g) along x direction

不同当量比下推进剂的填充高度如图10所示。由图10可见：在∈(05，20)范围内，随着当量比的增大，波头高度减小，+和总体上也呈现出逐渐减小的趋势，=05时波头高度最大为70 mm，=20时波头高度最小为52 mm。爆轰波波头高度随当量比增加而减小的主要原因是两方面因素的综合作用：一方面，爆轰波波头高度受爆轰波强度的影响，爆轰波越强，波后压力恢复就越缓慢，推进剂填充速度和填充时间减小，导致推进剂填充高度减小；另一方面，随着当量比增大，液滴数量增加，空气运动受到的阻力增大，导致新鲜空气填充高度减小。

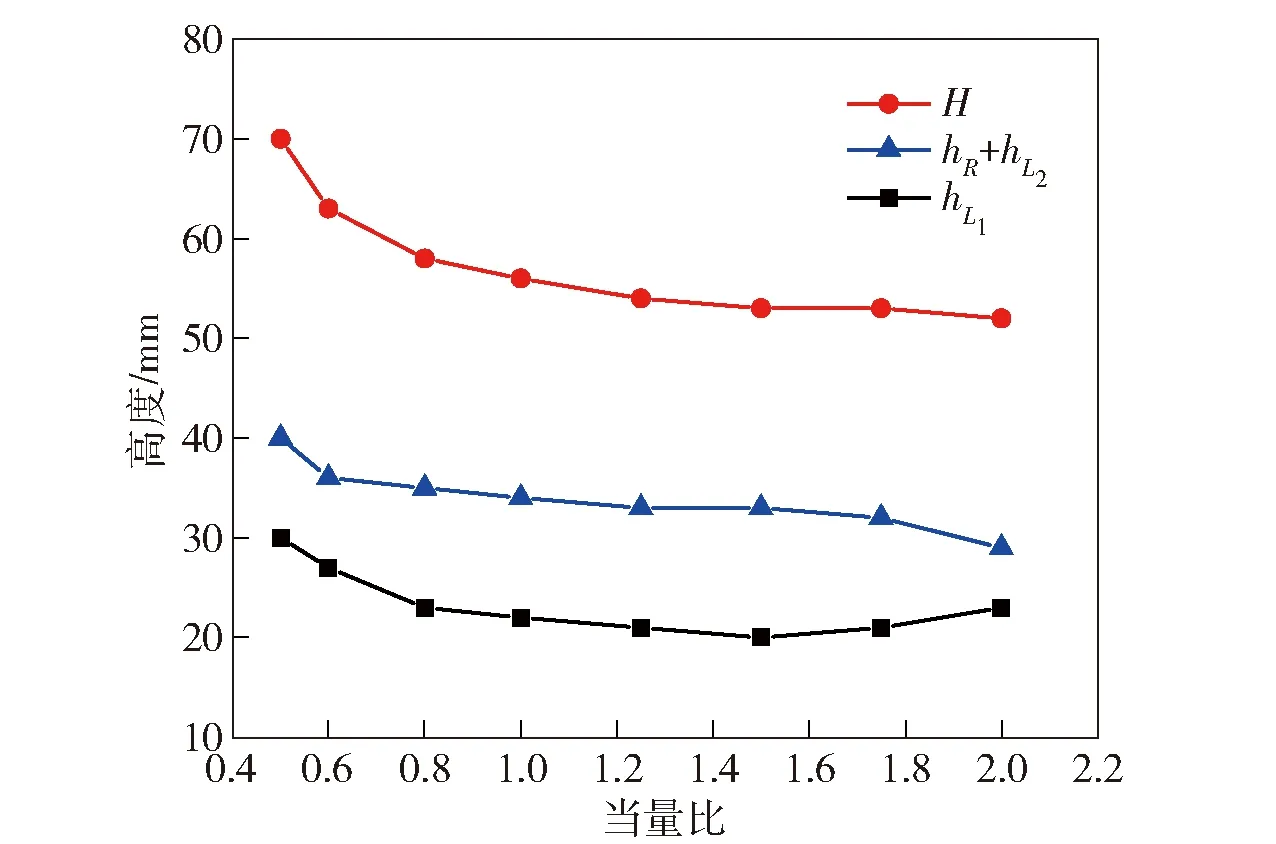
图10 推进剂填充高度随当量比的变化Fig.10 Propellant filling height vs.equivalent ratio

对于非预混条件下旋转爆轰燃烧的组织，在实际工程应用中，为了匹配流量，实现燃料与氧化剂的同步喷注是十分困难的，因此燃料淤积的情况是必然存在的，这将对旋转爆轰燃烧室的工作性能产生不利影响，因此本文以上的讨论对实际工程应用研究是具有一定指导意义的。

3.2 传播特性

=1时，监测点(=130 mm，=30 mm)处压力、波速和温度随时间的变化如图11所示。由图11可见：点火起爆后的前几个周期内，爆轰波压力峰值、波速存在较大波动，在传播7个周期后(>1.3 ms)，波速和压力峰值趋于稳定，结合入口流量曲线(见图12)可以发现，0 ms<<1.3 ms内，入口流量存在较大波动；当>1.3 ms时，入口流量波动幅度小于3%，并随着爆轰波的传播逐渐趋于稳定值(140 kg/s)；0 ms<<1.3 ms为旋转爆轰流场的自我调节过程，该过程内爆轰波强度、波前压力和推进剂流量相互影响，波动幅度逐渐减小并趋于稳定；爆轰波稳定传播阶段(1.3 ms<<5 ms)，爆轰压力、温度和波速的平均值分别为2.81 MPa、3 100 K和1 569.1 m/s，与气相理论值相比(见表1)，爆轰温度、压力与理论值的相对误差较小(小于4%)，而爆轰波速与理论值的相对误差为-12.2%，亏损较大，如3.1节所述，在新鲜反应物层内，一方面，液滴分布不均匀导致部分燃料未能参与爆轰燃烧，另一方面，煤油蒸气与空气混合不均匀，导致化学反应速率降低，这两点因素是造成爆轰波速度亏损的主要原因。另外，由图12可知，爆轰波稳定传播时，从喷注点进入燃烧室的煤油质量流量约为8.8 kg/s，出口煤油质量流量约为0.7 kg/s，这部分燃料未参与化学反应，燃料损失约为8%。

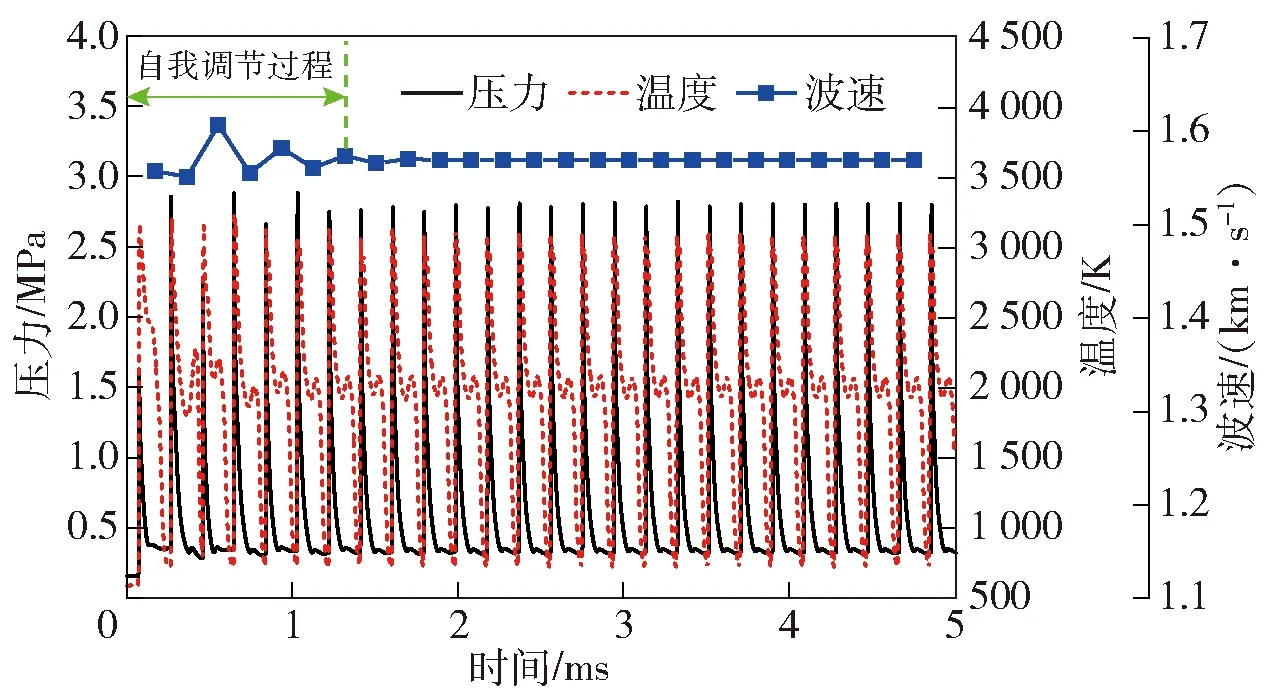
图11 爆轰参数随时间的变化Fig.11 Change of detonation parameters over time

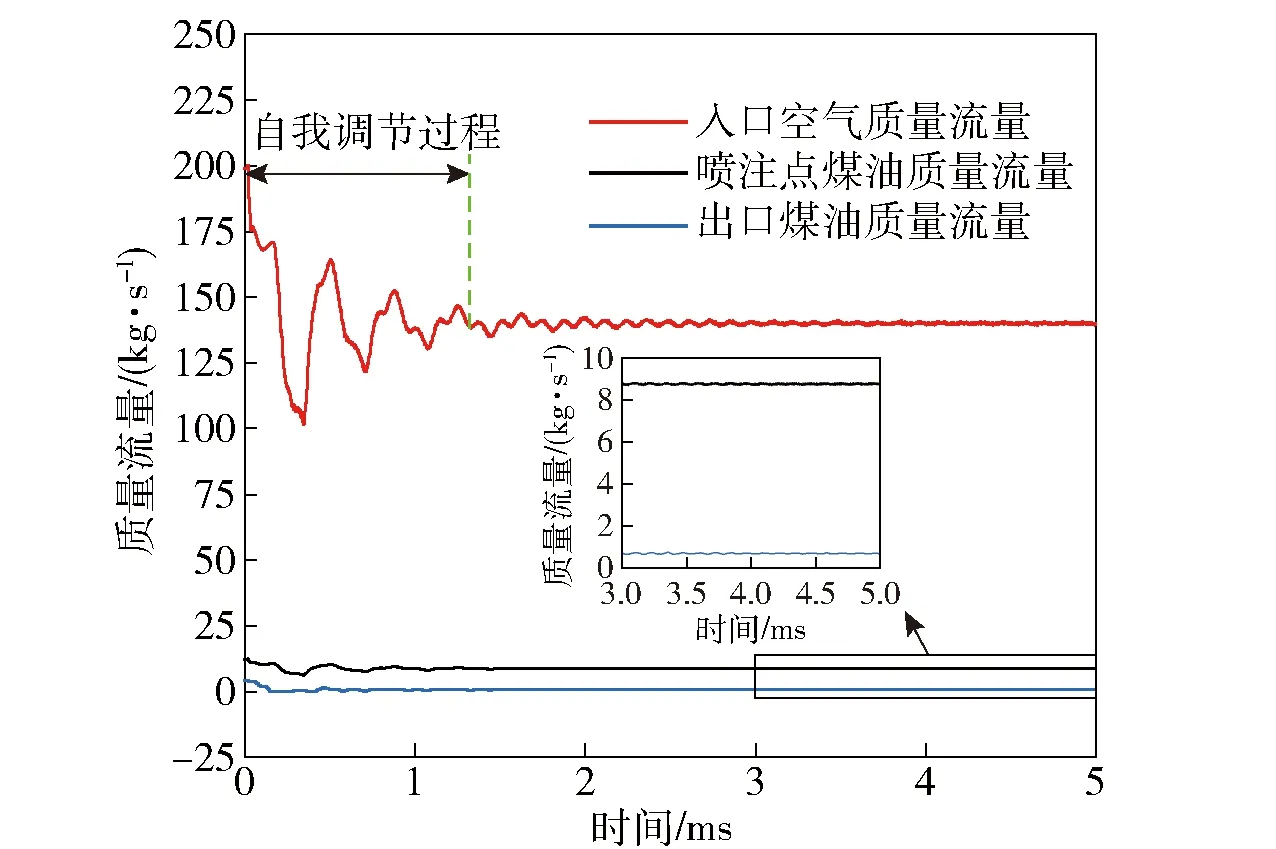
图12 质量流量随时间的变化Fig.12 Change of mass flow rate over time

沿=130 mm共设置5个监测点，这些监测点处压力峰值随时间的变化如图13所示，=10 mm位于区，爆轰波稳定传播时压力峰值约为2.4 MPa，=40 mm和=50 mm两个监测点位于区，爆轰波稳定传播时压力峰值较低，分别约为2.1 MPa和1.1 MPa，=20 mm和=30 mm 两个监测点位于区，爆轰波稳定传播时压力峰值分别约为2.5 MPa和2.8 MPa，高于其他区域的测点，结合气相爆轰的C-J理论值(见图14)可见，由于区对应较高的当量比，区对应的爆轰波强度最高，其次是区，区对应的爆轰波强度最弱。

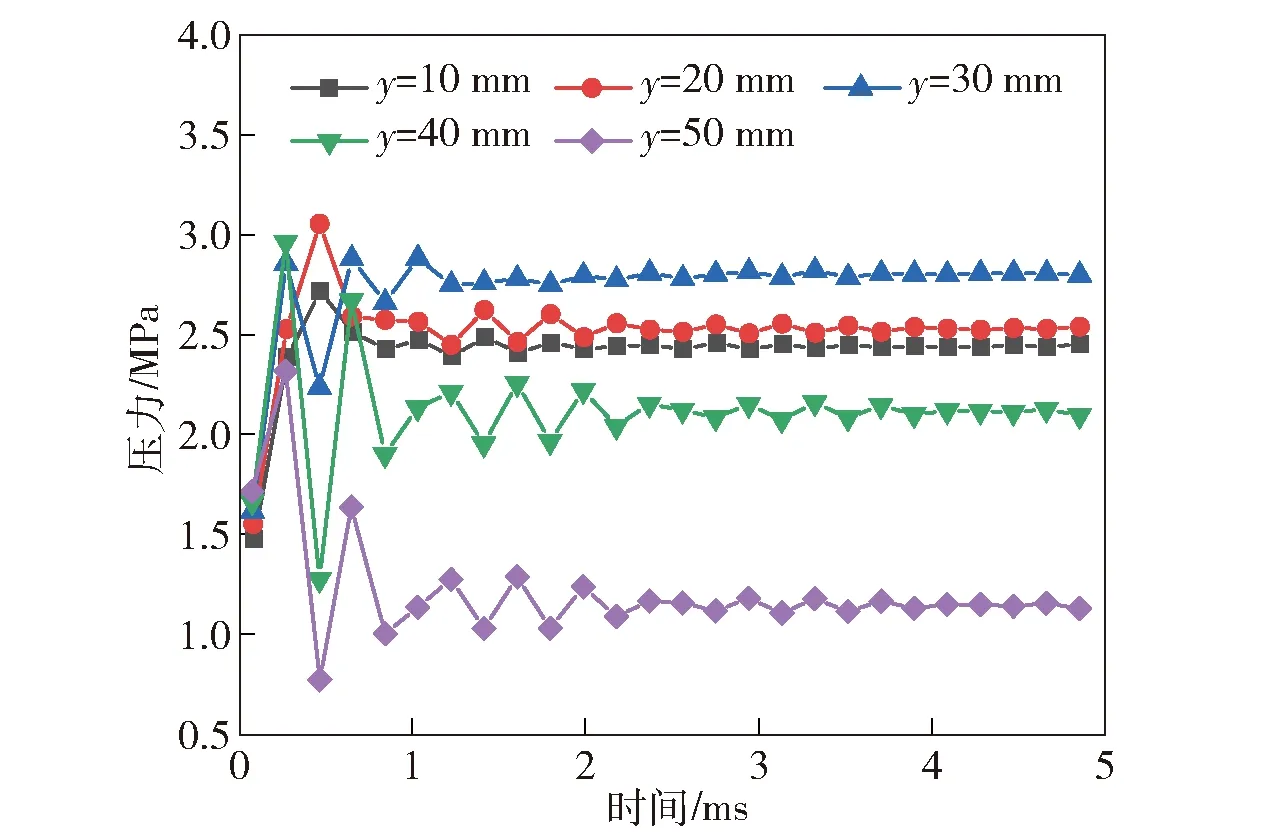
图13 不同监测点处压力峰值随时间的变化Fig.13 Change of pressure peak over time at different moniting points

爆轰波稳定传播时平均峰值压力、峰值温度和波速随当量比的变化如图14所示，图14中同时给出了对应条件下气相爆轰的C-J理论值，从中可见两相旋转爆轰波爆轰参数随当量比的变化趋势与理论值是一致的：=0.5时，爆轰波强度最弱，爆轰压力、温度和波速分别为2.08 MPa、2 745 K和1 388.4 m/s；随着当量比增加，爆轰波强度先增加后减弱，爆轰压力、温度和波速先增大后减小，在=1.5时爆轰波强度最高，对应的爆轰压力、温度和波速分别为3.29 MPa、3 134 K和1 604.0 m/s。

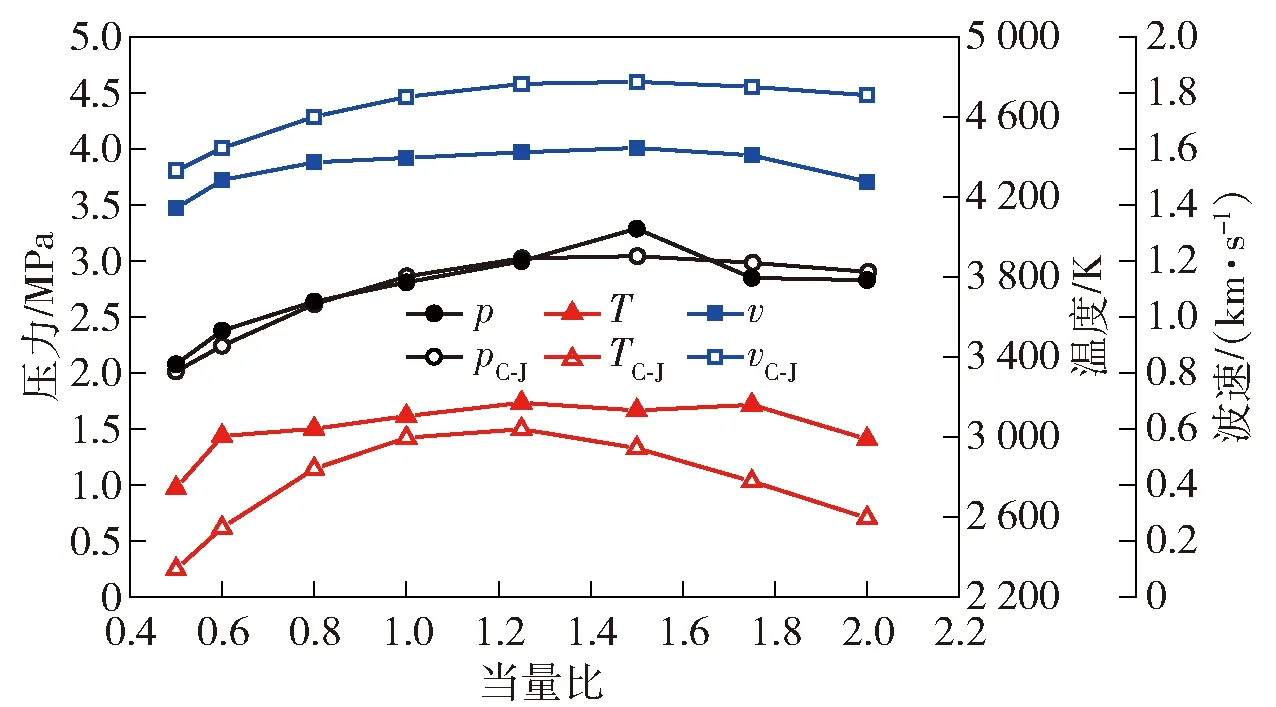
图14 爆轰参数随当量比的变化Fig.14 Detonation parameter vs.equivalent ratio

与理论值相比，两相旋转爆轰波的波速存在较大亏损，速度亏损随当量比的变化如图15所示。由图15可见：=0.6时速度亏损最小，为7.1%；随着当量比增加，未蒸发的液滴量增加，反应物的混合均匀性变差，速度亏损总体呈现增加趋势，=2.0时速度亏损最大，为17.2%；=0.5时速度亏损为8.9%，大于=0.6时的速度亏损，这可能是由于在低当量比下(<0.6)液滴数量少，液滴进入燃烧室后迅速蒸发为煤油蒸气，煤油蒸气的扩散速度已成为影响波速的主要因素。限于篇幅，该结论有待进一步验证。

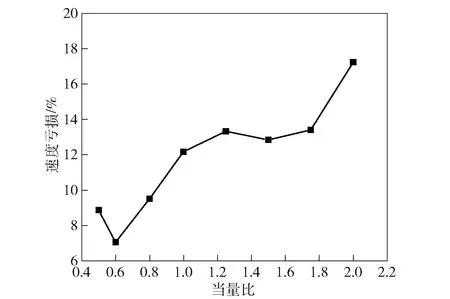
图15 速度亏损随当量比的变化Fig.15 Velocity deficit vs.equivalent ratio

燃料损失随当量比的变化如图16所示。由图16可见：≤0.6时燃料损失为0，进入燃烧室的所有燃料均参与了化学反应；=0.8时产生燃料损失(1.6%)；≥0.8时燃料损失随当量比的增大近似线性增加；=2.0时燃料损失最大，为51%。

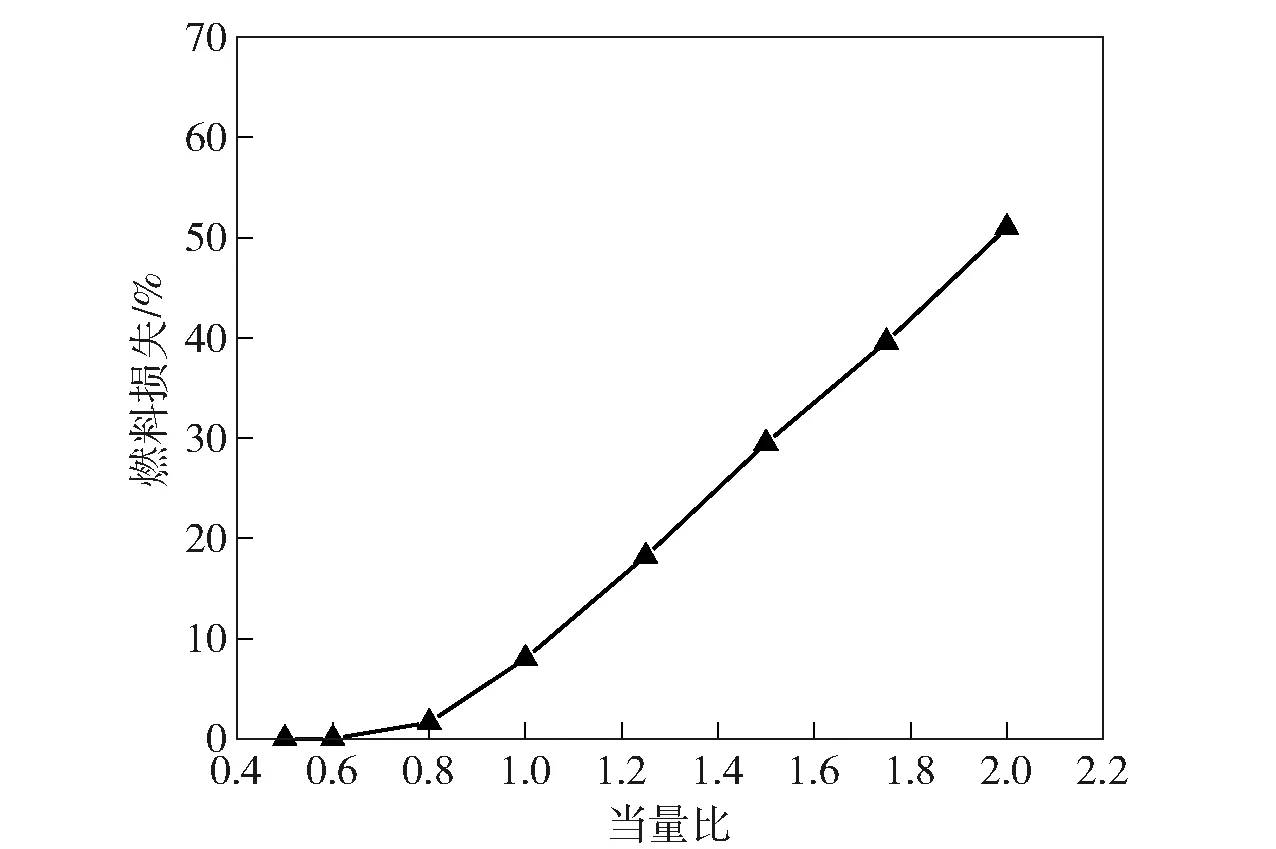
图16 燃料损失随当量比的变化Fig.16 Fuel loss vs.equivalent ratio

3.3 推力性能

为考察旋转爆轰燃烧室的推力性能，引入比冲和比推力，这两个参数分别反映了燃烧室消耗单位燃料或氧化剂产生推力的能力，它们的计算式如下：

(37)

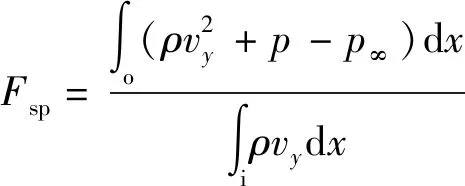
(38)

式中：为轴方向的速度分量；为标准大气压；=98 m/s。

=1时，比冲和比推力随时间的变化如图17所示。由图17可见：点火起爆后，比冲和比推力开始大幅度波动，随着旋转爆轰流场自我调节，比冲和比推力波动幅度逐渐减小并逐渐趋于稳定，爆轰波稳定传播时(1.3 ms<<5 ms)，比冲和比推力的平均值分别为2 384.8 s和1 463.0 N·s/kg。

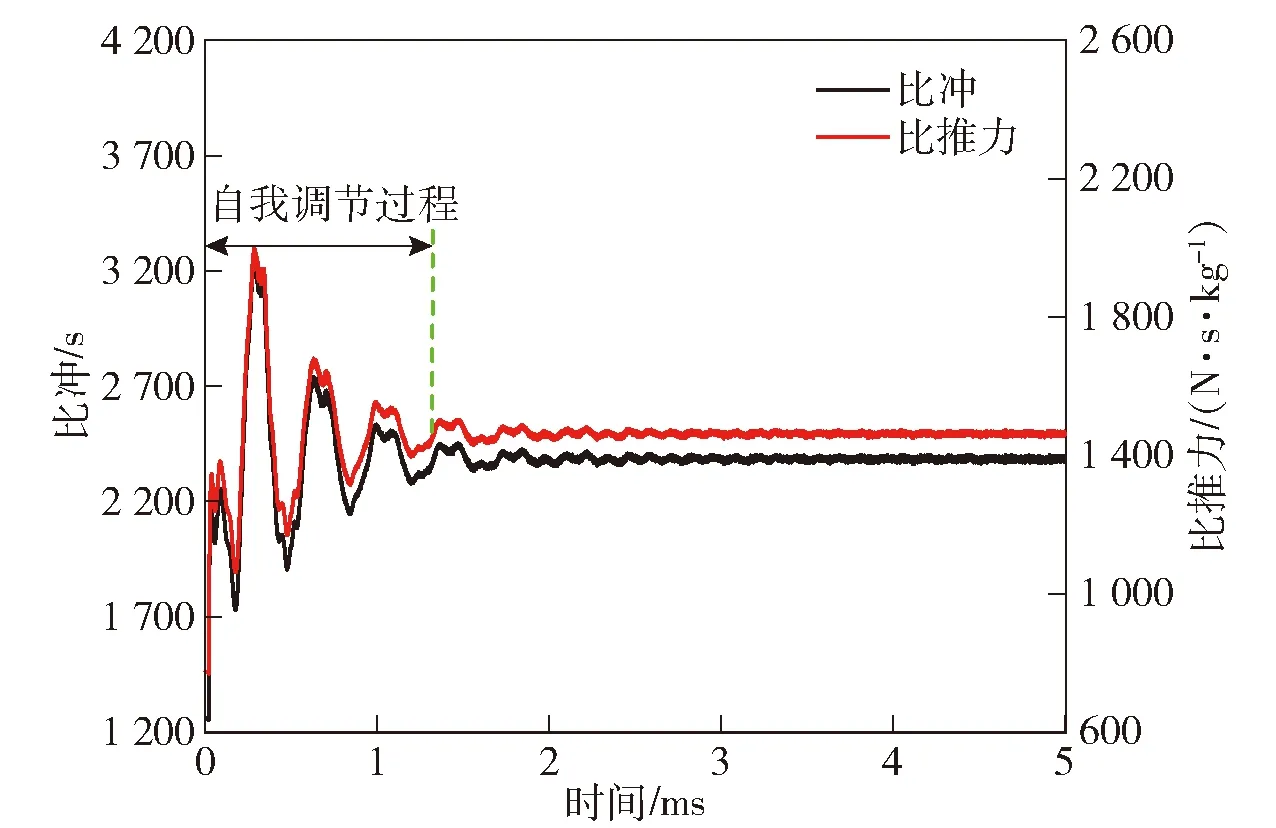
图17 比冲和比推力随时间的变化Fig.17 Change of specific impulse and specific thrust over time

爆轰波稳定传播时比冲和比推力随当量比的变化如图18所示。由图18可见：比冲随当量比的增大而减小，=0.5时比冲最大为3 912.4 s，=2.0时比冲最小为1 154.3 s；比推力随着当量比的增大先增加后减小，=0.5时比推力最小为1 226.8 N·s/kg，=1.5时比推力最大为1 521.8 N·s/kg。

图18 比冲和比推力随当量比的变化Fig.18 Specific impulse and specific thrust vs.equivalent ratio

4 结论

本文基于欧拉- 拉格朗日方法对常温液态煤油- 高总温空气两相旋转爆轰波进行了二维数值模拟，从理论上验证了常温液态煤油- 高总温空气两相旋转爆轰燃烧组织的可行性，研究了当量比对流场结构、传播特性和推力性能的影响。得出主要结论如下：

1)在靠近燃烧室入口的位置，煤油蒸气的质量分数较低且与空气混合不均匀，导致化学反应速率减小，爆轰波强度减弱，因此靠近入口位置的反应区滞后，爆轰波波头发生倾斜；受爆轰波强度和液滴数量等因素的影响，爆轰波波头高度随着当量比的增大而减小，=0.5时波头高度最大为70 mm，=2.0时波头高度最小，为52 mm。

2)来流空气与液滴初始速度的差异导致新鲜反应物层内形成液滴淤积区，淤积区存在大量未蒸发的煤油液滴，部分煤油没有参与燃烧并最终从出口排出，造成了燃料损失。≤0.6时燃料损失为0，=0.8时产生燃料损失(1.6%)，≥0.8时燃料损失随当量比的增大近似线性增加，=2.0时燃料损失最大，为51%。

3)反应物混合不均匀是导致两相旋转爆轰波速度亏损的主要原因，在当量比∈(0.6，2.0)范围内，随着当量比的增大，速度亏损总体呈现增加趋势，=0.6时速度亏损最小，为7.1%，=2.0时速度亏损最大，为17.2%。

4)爆轰波稳定传播时，比冲和比推力稳定，比冲随当量比的增大而减小，=0.5时比冲最大，为3 912.4 s，=2.0时比冲最小，为1 154.3 s；比推力随着当量比的增大先增大后减小，=0.5时比推力最小，为1 226.8 N·s/kg，=1.5时比推力最大，为1 521.8 N·s/kg。

在本文所采用的喷注条件下，发现液滴的淤积造成了燃料损失，尽管实际工程应用中燃料的喷注方式与本文并不完全相同，但显然实际工程应用中燃料与氧化剂的同步喷注是难以实现的，必然存在反应物混合不均匀的情况，反应物混合不均匀将导致更多的燃料不能参与爆轰燃烧，必然会影响燃烧室的工作性能，这可能是两相旋转爆轰燃烧室的研究中存在的新的技术问题，有待于进一步研究。