斜截头弹体入水的弹道特性
2022-07-05邵志宇伍思宇曹苗苗冯顺山
邵志宇,伍思宇,曹苗苗,冯顺山
(1.北京理工大学 机电学院,北京 100081;2.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
0 引言
随着智能水中弹药的发展,弹药开始起到侦查、识别、封锁等作用,抗冲击能力变弱。而弹药作用的有些水域深度较浅,有些弹药为了提高突防能力,入水速度较快。传统的对称型头部的弹体高速入水时形成空泡,与水的接触面较小,减速较慢,在浅水域容易撞击水底。非对称型头部产生的弯曲弹道可以较好地满足入水减速的要求。
对不同形状的对称头部弹体入水的研究已经比较深入,如Guo等研究了高速弹丸水平撞击水面的过程以及弹丸头部形状对速度衰减和相关力系数的影响。Miraei等讨论了高速弹丸入水的空化现象,建立了尾部撞击空泡壁时弹丸在空泡内运动的理论动力学模型。Wu等则通过试验和数值模拟研究了对称弹体入水过程以及相关的防护缓冲问题。魏卓慧等理论分析了刚性截锥形弹体入水速度、弹体头部参数和沾湿因子对入水冲击载荷的影响。自从von Karman在1929年提出刚体在入水过程中作用在刚体上冲击力的数学解后,产生了对入水问题的大量研究,而对于头部非对称偏头弹的相关研究较少。Shams等通过粒子图像测速实验得出了非对称楔形结构体入水的特性,并得出了水动力载荷的变化规律。王云等通过高速入水试验研究了椭圆斜截头弹体入水弹道的特性。华扬等也做了类似研究,其拍摄的弯曲弹道可为高速入水武器的研究提供参考。
目前,对于非对称弹体的理论研究还比较少,其形成的弯曲弹道并没有很好的理论模型来进行分析和预测。本文从理论出发,通过力学分析得出了斜截头弹体在入水过程中姿态偏转的数学模型;基于数值模拟提出了精准描述斜截头弹体入水弹道的经验公式;通过试验对姿态偏转数学模型、数值模拟和入水弹道经验公式进行了验证。
1 斜截头弹体垂直入水力学分析
图1为斜截头弹体的剖面图。图1中,为弹体直径,为弹体长度,为斜截长度,头部斜度定义为=。入水初始阶段的受力情况如图2所示。图2中,为水动力,和为的分力,为阻力,为旋转力,为旋转力矩,为和的夹角。

图1 斜截头弹体剖面图Fig.1 Profile of truncated cone-shaped projectile

图2 弹体入水初始阶段示意图Fig.2 Schematic diagram of projectile in initial stage of water entry
由于所受到的力不通过质心,其分力会产生旋转力矩。由于高速入水会产生空泡,此时弹体与水的接触面积很小,受力也很小,弹体只受到头部水动力的影响。水动力可由牛顿第二定律计算
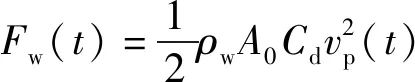
(1)
式中:为液体密度;为沾湿横截面面积;为力系数;为侵水瞬时速度,是时间的函数。降低了弹体的水平速度,而则提供了旋转力矩,使弹体旋转,从而失去稳定性。的计算公式为
()=()cos()
(2)
当弹体旋转时,垂直于弹体轴线的分量产生旋转力矩,导致旋转加速。角加速度与合扭矩之间的关系为
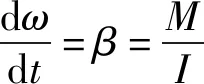
(3)
式中:为角速度;为角加速度;为转动惯量。
由于本文所研究的弹体长径比较大,非对称头部造成的质量损失相比于整个弹体质量非常小,弹体可以视为圆柱体。因此,质心位于几何图形的中心,弹体的姿态偏差可以看作是围绕质心旋转。在(3)式中,合力扭矩可以写成:
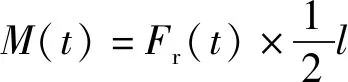
(4)
图3为转动惯量计算示意图,将弹体视为绕轴旋转的刚体。图3中,为弹体尾部击水力。

图3 弹体尾部碰撞空泡壁示意图Fig.3 Schematic diagram of projectile tail impacting on cavity wall
因此,需要确定弹体绕轴的转动惯量为

(5)
将(4)式和(5)式代入(3)式,可得角加速度随时间的函数为
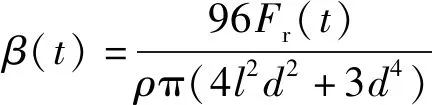
(6)
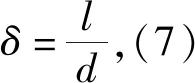
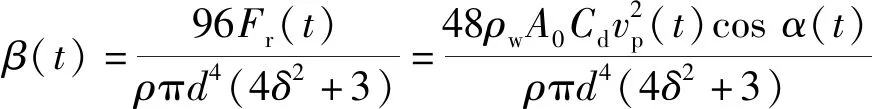
(7)
角速度表达式为
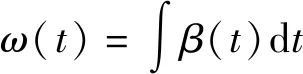
(8)
以上计算分析了弹体的姿态偏转,在弹体姿态发生偏转后,弹体失稳,尾部撞击空泡壁,导致产生尾流,如图3所示。随后弹体受到尾部击水力的作用,对弹体产生反向扭矩,减慢弹体角速度和水平速度,将引入(4)式中,可得

(9)
将(9)式代入(8)式,得
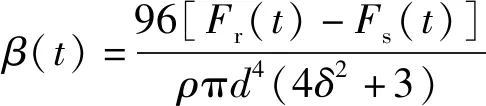
(10)
同时使弹体向垂直方向移动,进而发生弹道偏转。
根据(7)式、(8)式和(10)式可知,偏转角速度与阻力系数和头部斜度角有关,而阻力系数和方向角是由头部形状、侵彻速度、弹体密度和长径比决定的。从(7)式中可以总结出:侵彻速度越大,弹体偏转越快;密度、长径比越大,弹体偏转越慢。
2 数值模拟
用AUTODYN显式有限元软件进行数值模拟。采用二维数值模型进行入水计算,使用光滑粒子流体动力学(SPH)算法对入水过程进行模拟,SPH水域加上限制运动边界,模拟水箱以便于通过试验进行校核。采用拉格朗日网格法模拟弹体,重点研究弹体头部形状对弹道和姿态的影响,因此弹体被设置为刚体,模型如图4所示。弹体质量为65~1 000 g,长径比为8~20,入水速度为50~150 m/s,并且在模拟中考虑了8种头部斜度(=02,03,04,05,08,10,14,20)。在控制变量的基础上研究以上4种参数对弹体偏转的影响。由于控制变量时进行模拟的组别过多,表1仅列出了数值模拟的初始条件范围。忽略空气阻力和重力,将数据库中的材料参数用于弹体和水。

表1 数值模拟初始诸元Tab.1 Initial conditions of numerical simulation

图4 数值模拟模型(绿色为水,黄色为限制边界,蓝色为弹体)Fig.4 Numerical model (green is water,yellow is restricted boundary,blue is projectile)
表2为质量为65 g、长径比为8(直径20 mm,长度160 mm)、头部斜度=02的弹体以50 m/s入水的模型图和入水过程。由表2可见:入水初期弹体发生偏转,出现空泡;随着侵彻深度的增加,偏转角增大,弹体尾部撞击空泡壁,尾部的拍击使弹体发生垂直移动。
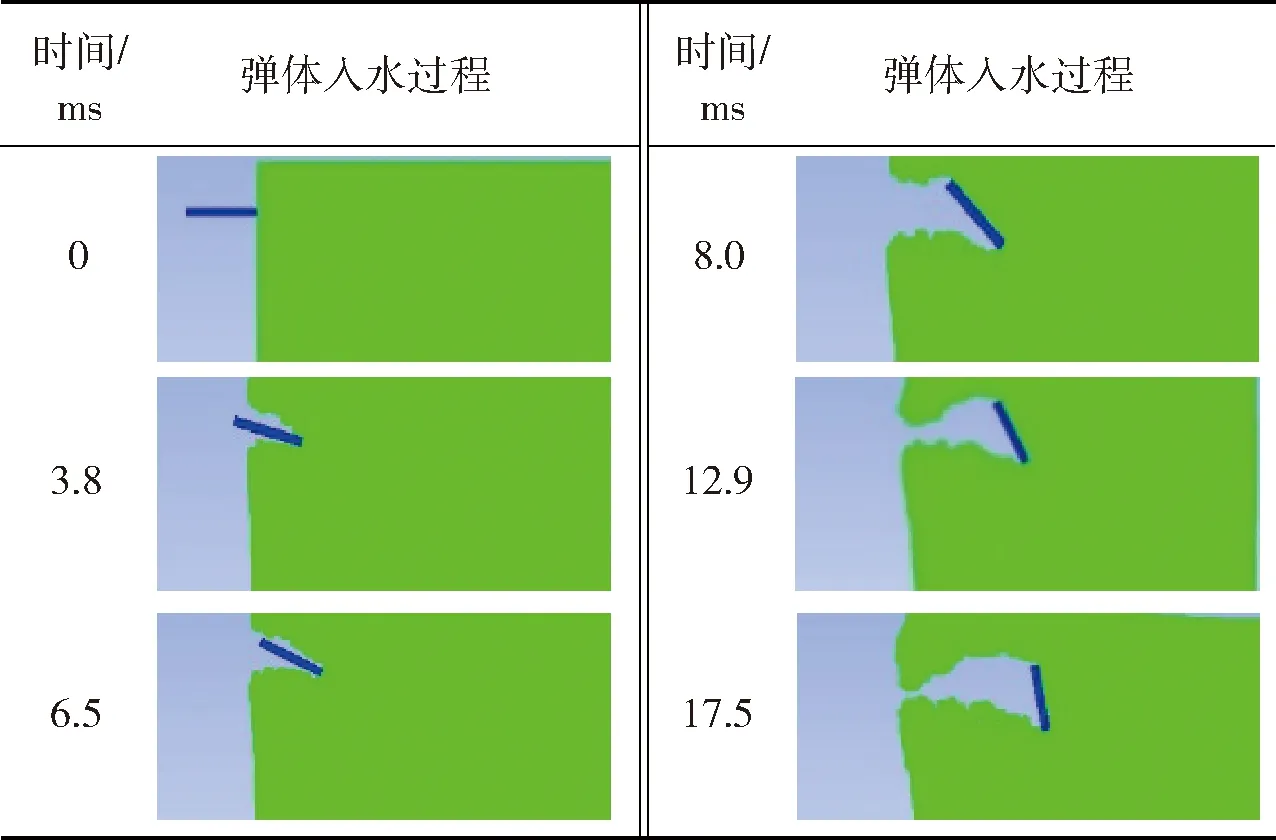
表2 数值模拟弹体入水过程(50 m/s)Tab.2 Simulated water entry process for ψ=0.2 at 50 m/s
通过控制变量法进行多组模拟发现,弹体入水偏转符合(7)式~(10)式,满足“侵彻速度越大,偏转越快;密度、长径比越大,偏转越慢”的结论,在后文的试验研究中将对该结论进行进一步论证。但是头部斜度对姿态偏转的影响却是有一定限度的。图5为不同斜度头部的弹体入水姿态偏转结果,弹体质量均为65 g,长径比为8(直径20 mm,长度160 mm),入水速度为50 m/s。从图5中可以发现:当02<<05时,姿态偏转速度随着头部斜度增大而增大,与(10)式相符,偏转90°所需要的时间明显减小;当>05时,偏转90°所需要的时间差别不大,即头部斜度在一定范围内对弹道有影响,当达到某一值后,对弹道的影响就变得很小。

图5 不同头部斜度弹体的姿态偏转Fig.5 Attitude angle deviation of projetiles with different inclination nose shape
为探讨入水速度对弹道的影响,对比分析相同弹体(质量为65 g,头部斜度为1,长径比为8)在不同入水速度下的质心弹道,并做了更高速度入水的数值模拟(低于音速),弹道对比如图6所示。由于在真实情况下竖直入水研究更有意义,本文的研究均忽略了重力,得出的弹道图均等效为竖直入水的情况。经对比发现,不同速度入水的弹体其弹道基本相同,只是通过弹道的时间有所不同,入水速度虽然会影响弹体弹道偏转和姿态偏转的快慢,但对于弹道没有影响。本质上弹体的受力是由瞬时速度和阻力系数决定的,而阻力系数与弹体的沾湿面积和表面形状有关。虽然不同速度入水的弹体受力大小不同,但是水平和竖直方向上所产生的位移比是定值。由于不同入水速度的相同弹体弹道重合,可以推断不同入水速度下的弹体所经历的受力过程相同,只不过快慢不同,弹道由弹体的头部形状、长径比、质量决定。
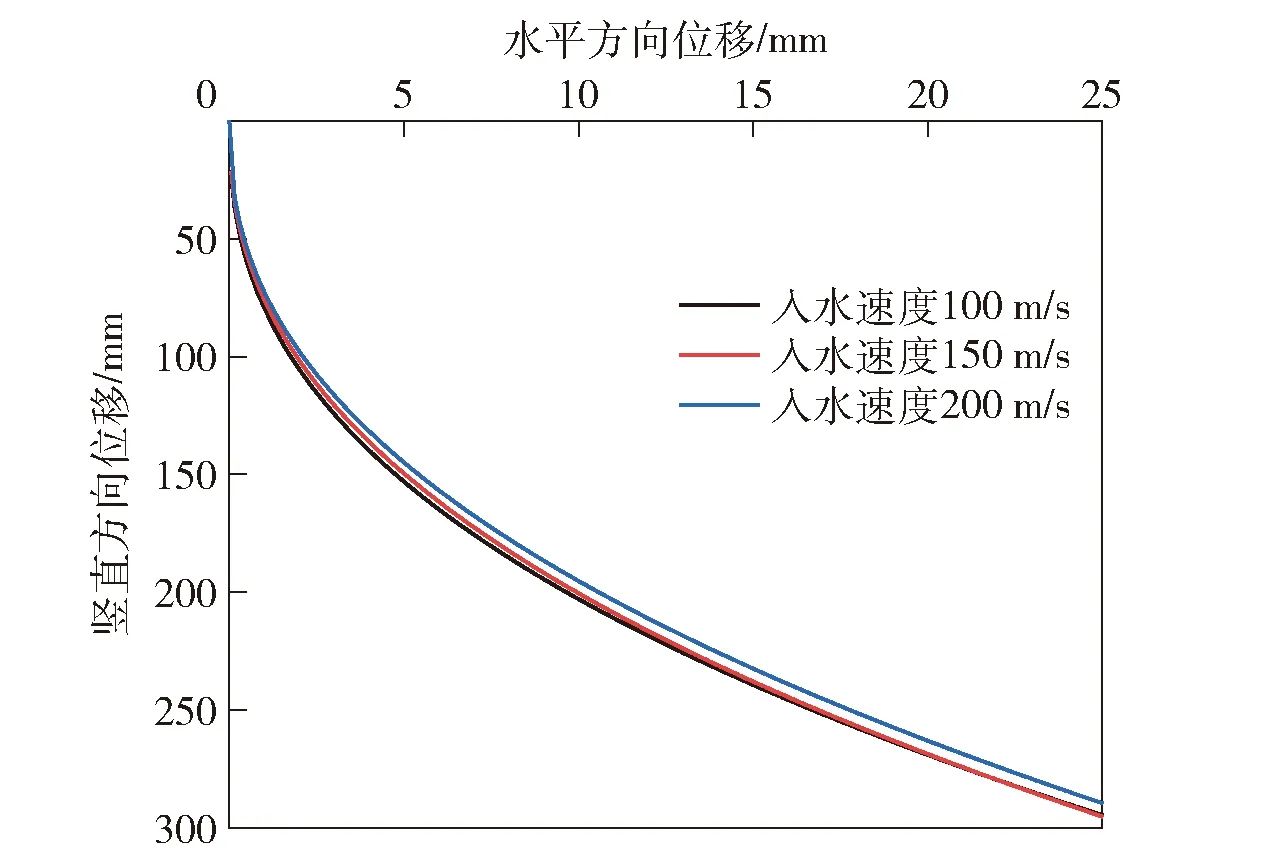
图6 不同入水速度下的偏转弹道Fig.6 Deflecting trajectories at different muzzle velocities
3 质心弹道经验公式
斜截头弹体入水的各项参数有头部斜度、入水速度、长径比和质量,对于姿态偏转,它们的变化规律满足(8)式和(9)式。下面基于数值模拟提出斜截头弹竖直入水的质心轨迹方程。由于斜截头弹体入水弹道为弯曲弹道,对这种弹道进行预测具有重要工程意义。头部斜度>05和入水速度(低于声速)对质心弹道影响非常小,对弹道影响最大的因素是弹体质量和长径比。斜截头弹体质心轨迹具有良好的幂函数关系,考虑到实际情况中是竖直入水,据此建立一个新的方程来描述:1)竖直入水弹道;2)弹体质量;3)头部斜度(>05)的弹长径比之间的关系。方程的形式为
=(,,)
(11)
式中:为竖直深度;为水平位移。(11)式为一个三元函数关系式,要拟合三元函数关系式,就需要大量数据,因此按照SPH仿真方法,改变弹体参数和入水条件进行大量模拟,参数如表3所示。分别选用5种长径比,每种长径比设置5种质量,弹体头部斜度均为1,入水速度为100 m/s。
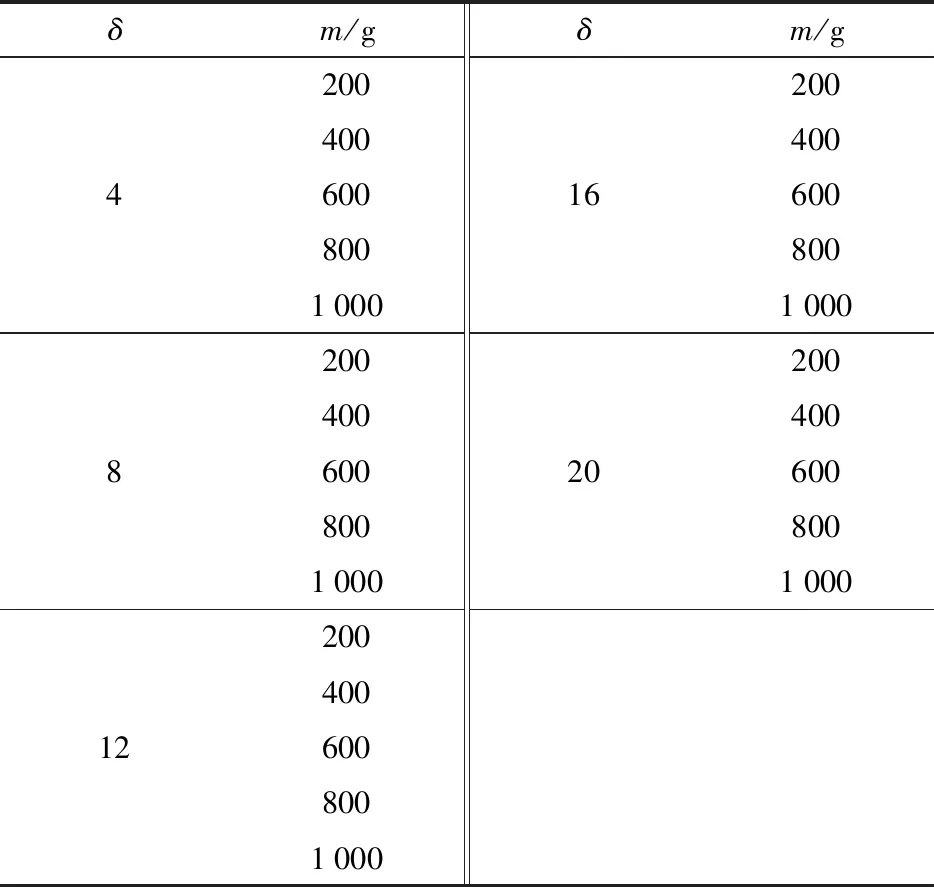
表3 竖直入水质心轨迹模拟初始条件(ψ=1,v=100 m/s)Tab.3 Initial conditions of vertical water-entry simulation (ψ=1,v=100 m/s)
图7为不同质量弹体在不同长径比下的质心轨迹,根据图7中的曲线,质心轨迹满足幂函数,
=
(12)
式中:参数、与质量和长径比有关。参数和根据图7的拟合值如表4所示,拟合优度值接近1,表示拟合准确度越高。
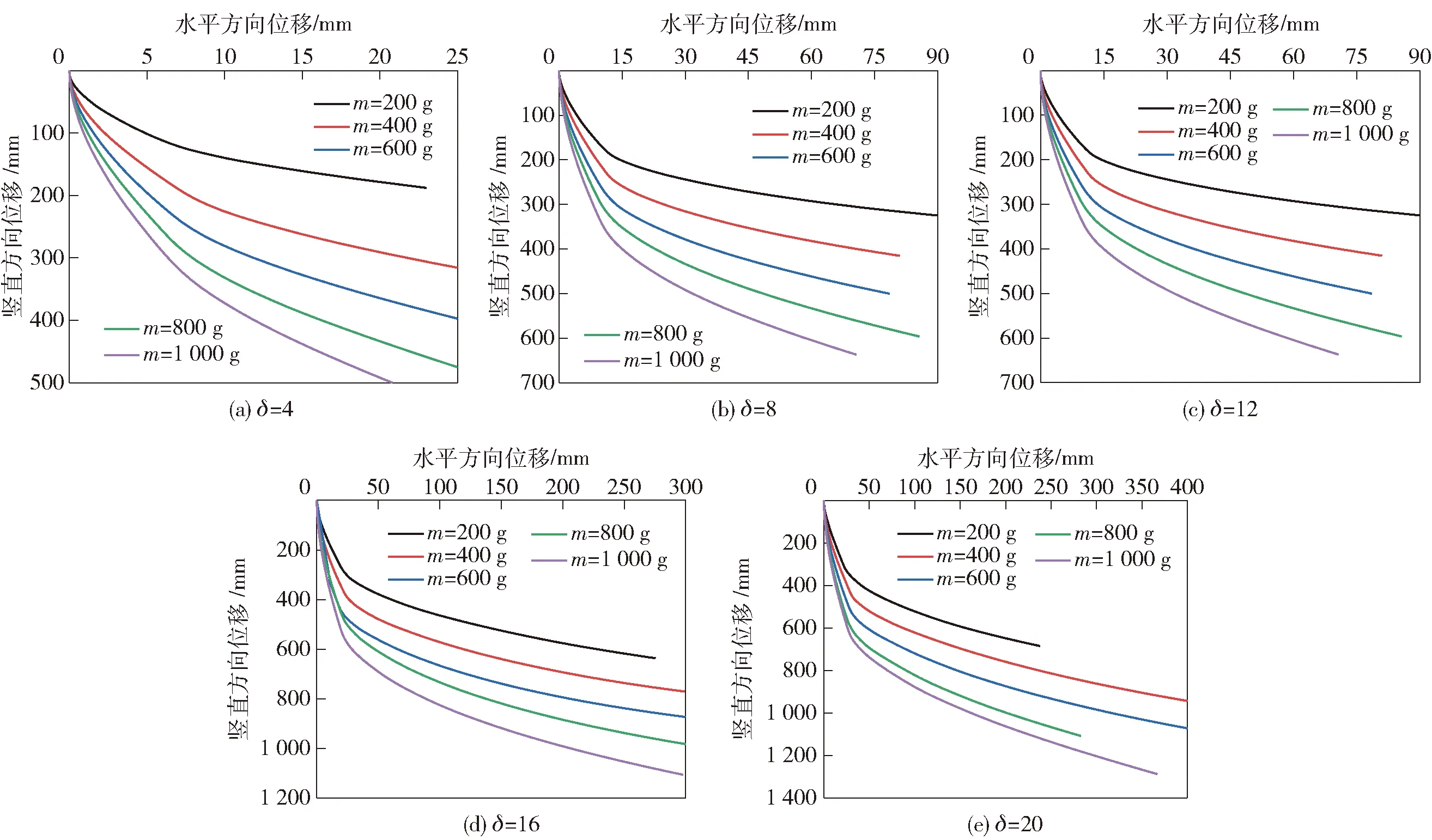
图7 不同状态下斜截弹体入水质心轨迹数值模拟结果Fig.7 Center of mass trajectory of projectile under different length-to-diameter ratios
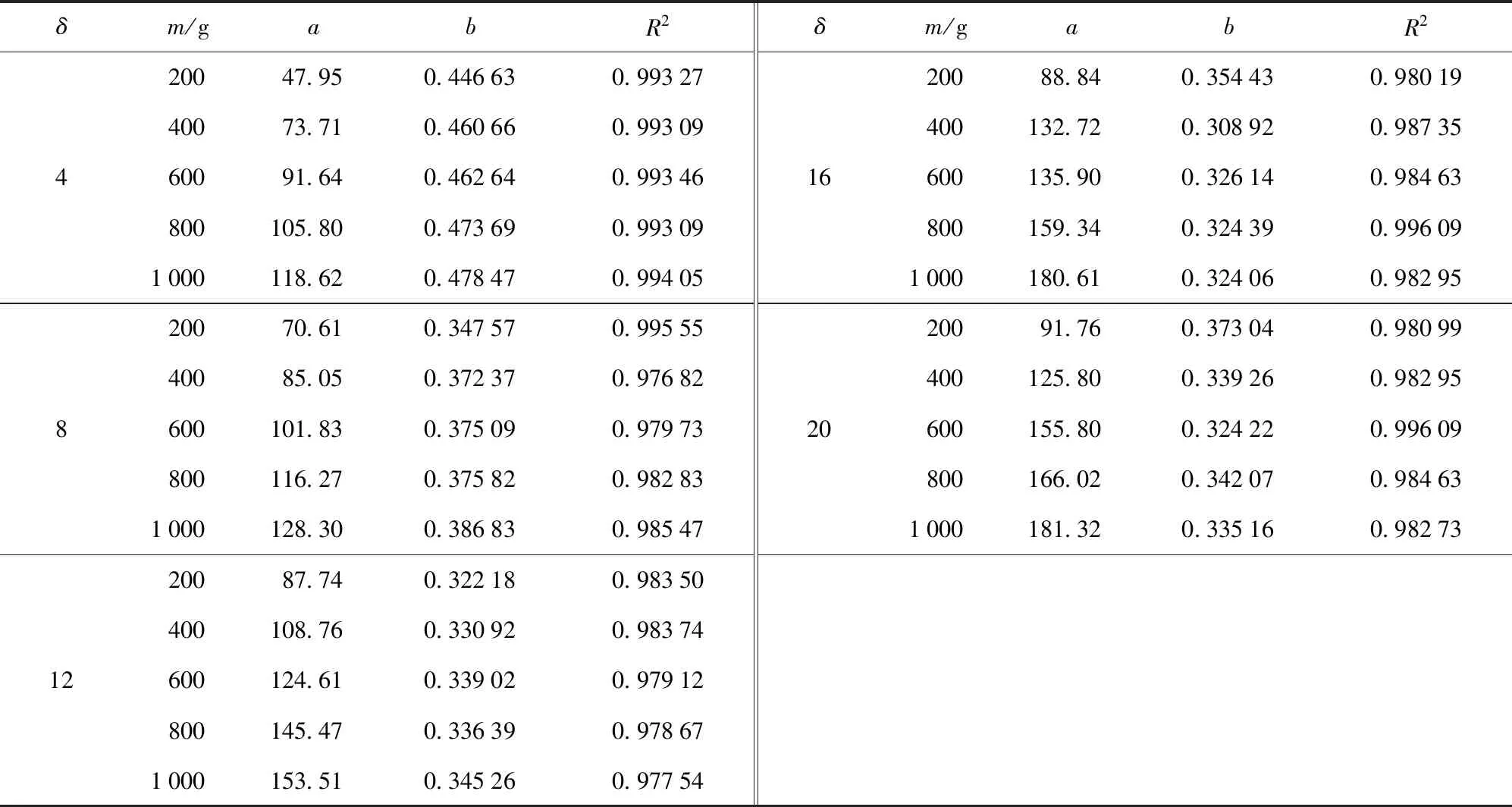
表4 不同条件下参数a、b的拟合值及曲线拟合的优度Tab.4 Best fitted values of a and b
图8为参数与弹体质量的关系,可以看出长径比一定时与质量呈线性关系,因此可以表示为
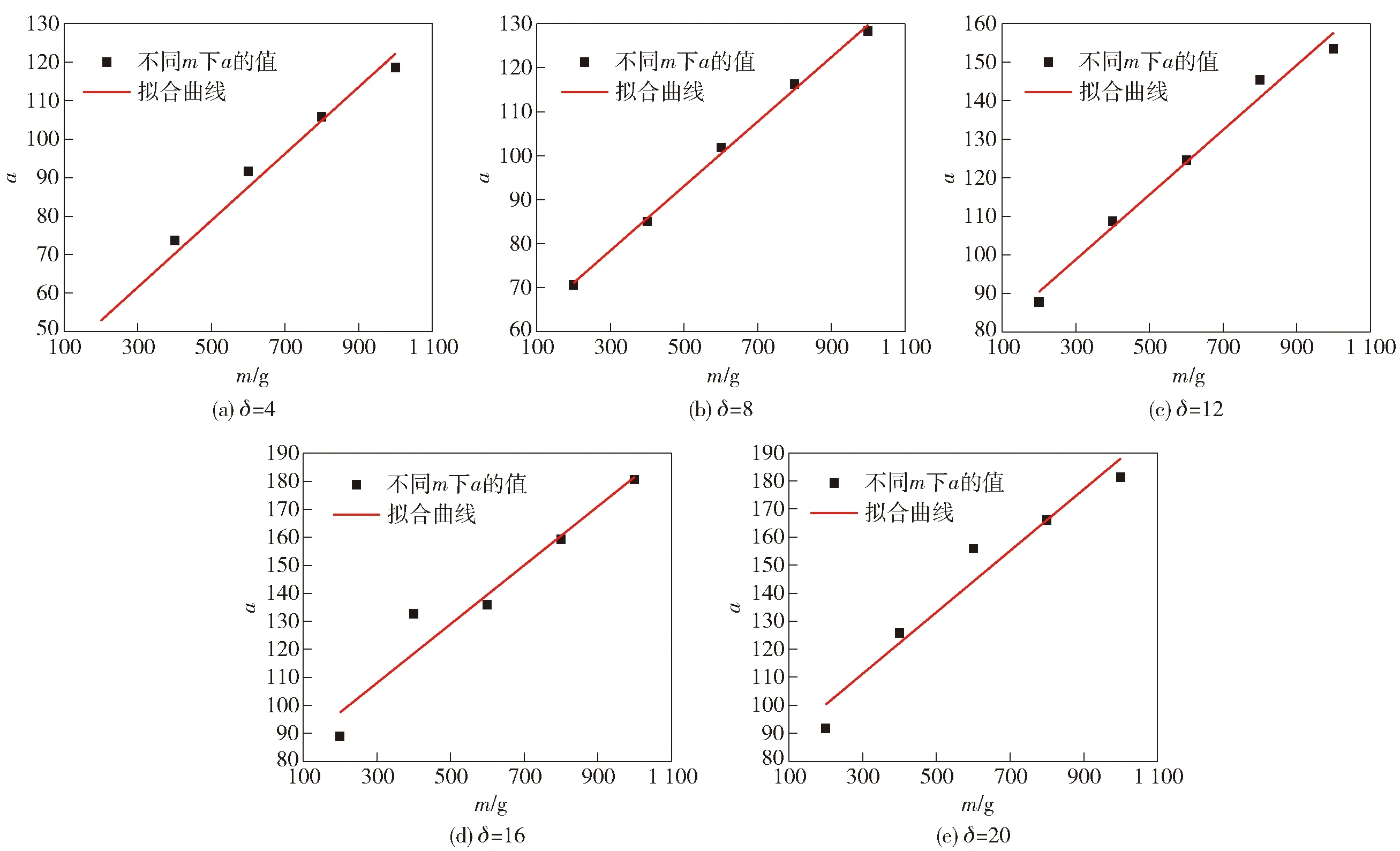
图8 不同长径比条件下参数a与弹体质量的关系Fig.8 Relationship between parameter a and mass of projectile under different length-to-diameter ratios
=+
(13)
式中:和为的参数。
图9为与弹体质量的关系,可以看出长径比一定时,随质量的变化量非常小,可以视为一个常数,因此可以表示为
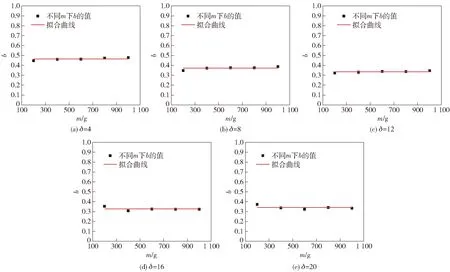
图9 不同长径比条件下参数b与弹体的关系Fig.9 Relationship between parameter b and mass of projectile under different length-to-diameter ratios
=
(14)
式中:为的参数,在质量一定时为常数。
将和代入(13)式,质心轨迹方程可以写为
=(+)
(15)
参数、、在不同长径比下的数值如表5所示。表5给出了线性拟合公式(13)式的拟合优度和常数拟合公式(14)式的方差。

表5 参数k、t、c拟合值Tab.5 Best fitted values of k,t,and c for different length-to-diameter ratios
图10表示长径比与参数、、之间的拟合关系。从图10中可以看出,为常数值,、与符合幂函数关系,因此这3个参数关于长径比的表达式为
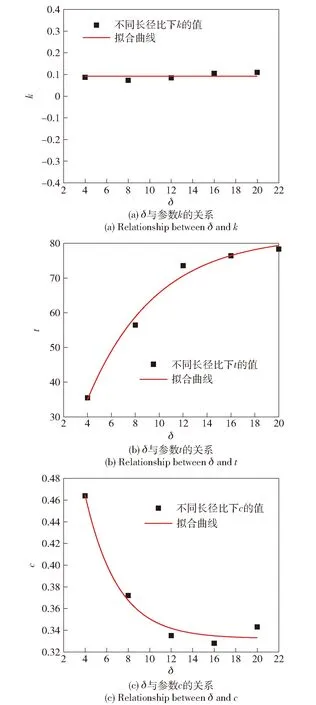
图10 长径比δ与参数k,t,c的关系Fig.10 Relationship between δ and k,t,and c
=
(16)

(17)
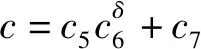
(18)
式中:~为拟合参数,具体数值由表6给出。

表6 (20)式中的拟合参数值Tab.6 Best fitted values of the constants in Eq.(20)
因此,质心弹道方程可以写为
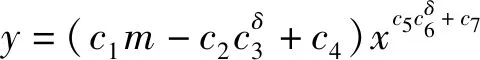
(19)
4 试验研究
4.1 试验方案
图11为试验装置的原理图。图11中,水箱为08 m×08 m×10 m的聚碳酸酯复合材料制成的开放、透明、抗冲击立方体;前后有2个孔,用两块02 mm厚的丙烯酸隔膜密封,确保不会影响入水过程。利用高速摄影机记录流体、弹体和弹道偏转的初始速度和运动过程。获得图像后通过软件测量弹体速度、位移、偏转角等参数。试验用缩比弹从一个标准火炮装置发射,瞄准水箱的隔膜。为确保弹体偏转被高速摄影机记录,入水的角度被设置为尽可能垂直于水面,并防止弹体旋转。另外,在发射管内填充尼龙弹托,以减少发射气体对弹体的冲击,保证斜头弹体的入水姿态。此外,采用低燃速推进剂来降低发射气体对弹体姿态的影响。通过调整装药中推进剂的质量来调整弹体的加速度和初速度。针对弹体入水偏转的研究中采用直径为20 mm的试件,它们通过前孔水平射入水箱,每做完一次试验都重新装水,并用新的隔膜密封水箱。
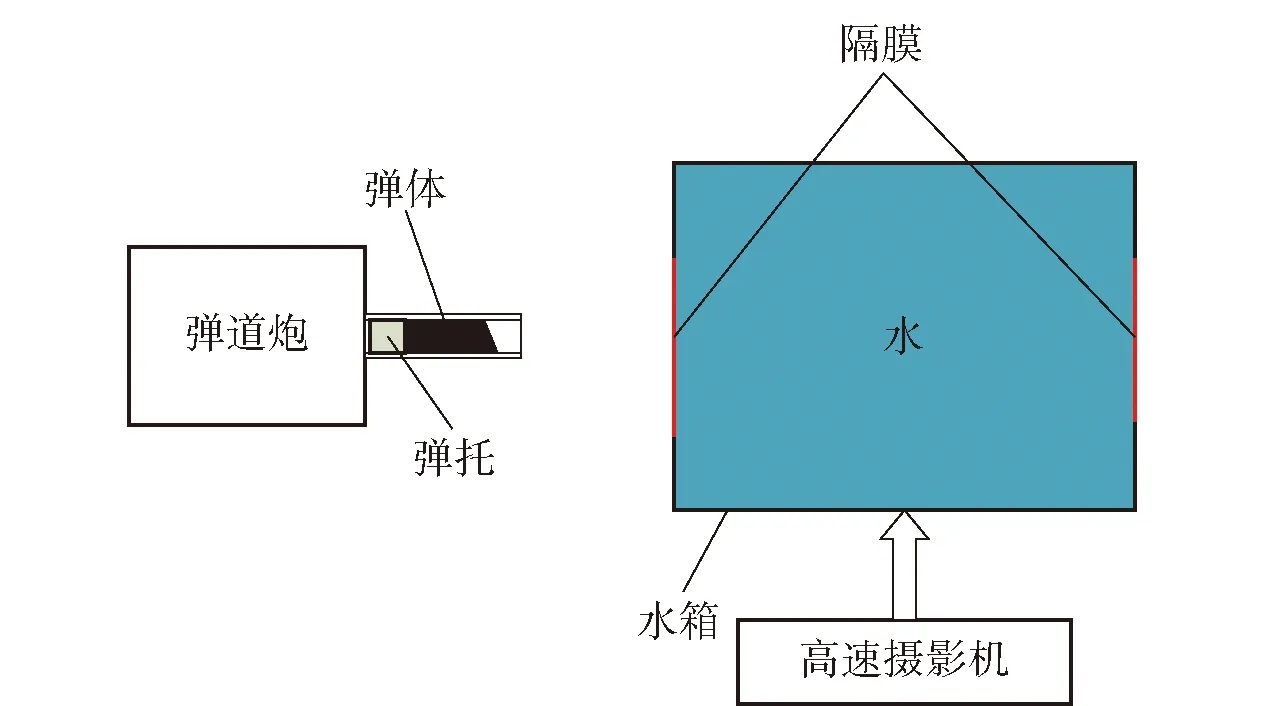
图11 试验装置原理图Fig.11 Schematic diagram of experimental system
试件截面形状与图1相同,表7为10种不同试验弹体的初始状态,包括质量、长径比、头部斜度和入水速度,为了对(9)式进行验证,用控制变量法:

表7 入水偏转试验诸元Tab.7 Initial conditions of underwater trajectory deflection experiment
1) 样本3、5、8选用3种不同密度的金属材料,以保证它们除了质量以外,其他初始条件一样,以对比分析质量对弹体偏转的影响;
2) 样本6、7、8除长径比不同,其他初始条件相同,以对比分析长径比对弹体偏转的影响;
3) 样本1、2、3除了头部斜度不同以外,其余条件相同,以对比分析头部斜度对弹体偏转的影响;
4) 样本4、8、9除了入水速度不同,其余条件相同,以对比分析撞水速度对弹体偏转的影响。
5) 样本10为平头弹体,作为对照组。
4.2 试验结果分析
表8为平头弹和斜截头弹入水过程的高速摄影图片。由表8可以看到:平头弹体由于其对称性,能较长时间在水中保持稳定,形成空泡,因此沾湿面非常小,不利于减速,最终以较高速度从水箱另一侧隔膜穿出;斜截头部弹体入水后迅速失稳,发生姿态偏转,随后尾部撞击空泡壁,沾湿面瞬间增大,有利于弹在水中的迅速减速。两种弹体入水初始姿态均为垂直于水面,如图12所示,定义弹体偏转后弹轴与竖直方向夹角为弹体的偏转角。

表8 平头弹与斜截头弹入水过程对比Tab.8 Comparison of water-entry process between projectiles with flat nose and oblique nose
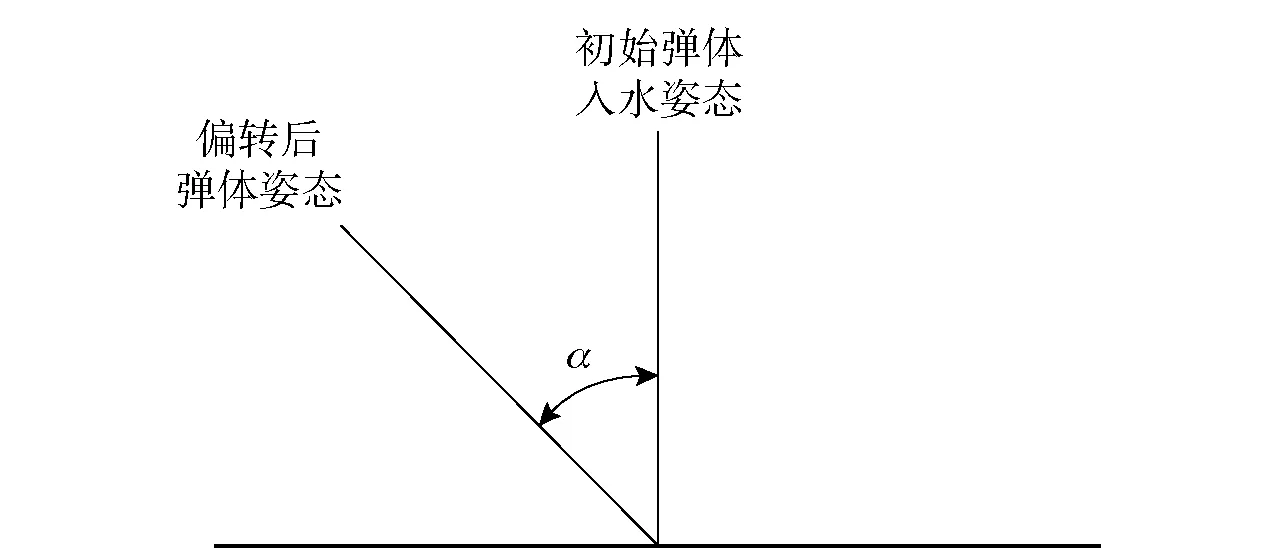
图12 偏转角α示意图Fig.12 Deflection angle α
图13为试验中通过高速摄影机测出的不同条件下弹体姿态随时间的偏转曲线。由图13可见:头部斜度为02与05对弹体姿态偏转影响很大,为05与10时对弹体姿态偏转影响不大,符合数值模拟结果;入水速度越大,姿态偏转越快;弹体的长径比与质量越大;偏转越困难。综上所述,通过试验得出的结论与理论分析和数值模拟的结论吻合。

图13 不同条件下弹体姿态随时间的偏转曲线Fig.13 Attitude deflection history under different conditions
5 对比验证
5.1 数值模拟有效性验证
=02时试验与数值模拟入水偏转过程对比如表9所示。由表9可见:弹体入水的姿态变化与试验一致性较好;入水初期发生偏转,出现空化效应;随着侵彻深度的增加,偏转角增大,弹体尾部撞击空泡壁;尾部的拍击使弹体垂直移动。图14表示弹体入水过程中时间与偏转角的关系。由图14可见,模拟结果与试验结果一致性较好,误差在可接受范围内,证明了仿真方法的有效性,能够有效地反映弹道偏转过程的细节。

表9 试验与数值模拟入水偏转过程对比Tab.9 Comparison between experimental and numerical water entry processes
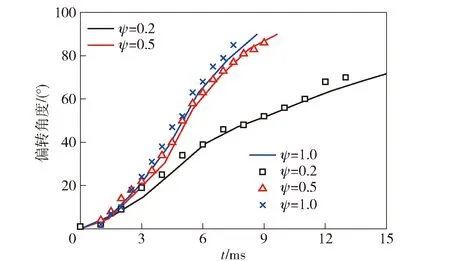
图14 约50 m/s入水速度下偏转角的变化曲线Fig.14 Attitude deflection histories of projectiles with different nose shapes at about 50 m/s
5.2 弹道经验公式有效性验证
通过拟合数值模拟得出头部斜度>05的弹体入水的质心轨迹方程,试验部分中1号样本为>05的弹体。提取1号样本的质心轨迹,提取方法如图15所示。将=8、=622 g代入(19)式,计算出质心轨迹方程。由于忽略了重力,水平入水的弹道与竖直入水的弹道是相同的。将两种方法得到的质心轨迹方程进行对比,结果如图16所示,可见二者的一致性较好,误差在可接受范围内,证明弹体质心轨迹经验公式是有效的。

图15 描边法提取弹体位置与姿态Fig.15 Projectile position and attitute extraxted by boundary representation
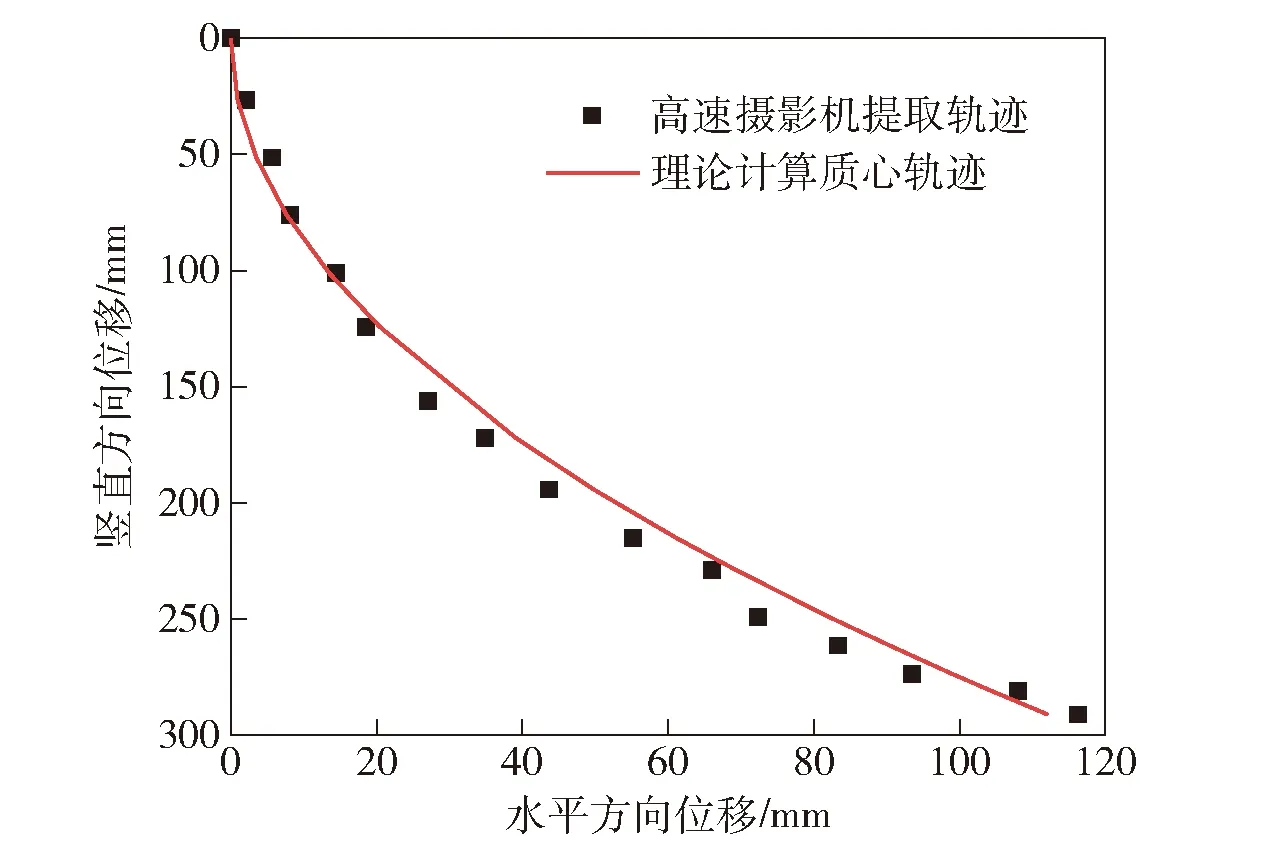
图16 试验弹道与计算弹道对比Fig.16 Comparison of experimental and calculated trajectories
6 结论
1) 针对斜截头弹体,结合数值仿真和试验结果可知,当头部斜度<05时,弹道的偏转会随着的增大而增大;当>05时,其对轨迹的影响较小。
2) 提高撞击速度可引起水动力偏转力矩增大,进而提高了角加速度,因此姿态偏转会更快。
3) 质量和长径比越大,转动惯量越大,偏转角加速度越低,因此弹道的弯曲程度与质量和长径比呈反比。
4) 数值模拟得到的入水过程和偏转角度与试验结果吻合较好。
