关于Smarandache函数的Möbius变换与欧拉函数

廖群英, 白海荣, 董 坤

(四川师范大学 数学科学学院, 四川 成都 610066)

1 引言及主要结果

1993年,Smarandache[1]首次定义了正整数n的Smarandache函数

S(n)=min{m:m∈N,n|m!}.

为叙述方便,设p、q、γ均为素数,τ(n)、ω(n)和p(n)分别为正整数n的正因子个数、不同的素因子个数和最小的素因子,ω(M)为集合M中所有元素的不同素因子个数,并记:

A1={2t,t≤6},

A2={24p(p=5,7),23p,22×52}∪

{22p,2p2(p=5,7),2p},

A3={22×5p(p=7,11,13),

2×7×11,2×5p},

B1={34×2,33×2t(t≤3),

32×2t(t≤4)}∪{3×2t(t≤6)},

B2={33×2×5,32×23×5,32×2p}∪

{32×22p(p=5,7,11,13),3×25×5}∪

{3×23p,3×24p(p=5,7),3×22×52}∪

{3×22p,3×2p2(p=5,7),3×2p},

B3={3×22×5p(p=7,11,13)}∪

{3×2×7×11,2×3×5p},

其中

ω(Ai)=i,ω(Bi)=i+1, 1≤i≤3.

1)n=p≥5;

2)n∈{3t(1≤t≤3),3p(p≥5),32×5};

定理 1.3设p≠q,n∉{1,p,pq}且p(n)≥5,则

2 相关引理

为后文叙述方便,记:

C1={1,3,5,7,9,11,13,15}∪

{21,27,33,35,39,45,63,105},

C2={1,3,5,7,9,11,15,21,27,33,45},

C3={1,3,5,7,9,15,21},

C4={1,3,5,9,15},C5={1,3}.

为证明本文的主要结果,需要如下几个引理.

引理 2.1[11]设n为正整数,则

特别地,若n为正奇数,则

引理 2.2设n为正整数,则

此时

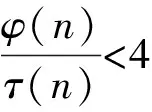
现设i≥1,直接计算可知:

D1={1,3},D2={5,9,15},

D3={7,21},D4={45,27},

D5={11,33},D6={13,35,39,63,105},

1)n=2m,m∈C1;

4)n=24m,m∈C4=D1∪D2;

5)n=25m,m∈C5=D1.

这就完成了引理2.2的证明.

引理 2.3设p为素数,n为正整数,且

则当p=3|n或p≥5时,有

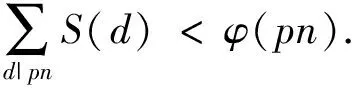
证明等价地,只需证明

事实上,易知

以及由题设条件及引理2.2知φ(n)≥4τ(n).进而,若n的标准分解式为n=p则α=0时,有

(p-1)φ(n);

而α≥1时,有

φ(pn)=(p-1)p

p(p-1)p

因此,当p=3|n时,有

φ(3n)-φ(n)=2φ(n),

从而

3τ(n)=(φ(n)-τ(n))-2τ(n)>0.

当p≥5时,有

φ(pn)-φ(n)≥(p-2)φ(n),

从而

(p-3)φ(n)-pτ(n)=

(p-3)(φ(n)-τ(n))-3τ(n)>0.

这就完成了引理2.3的证明.

引理 2.4若

n∈{pt(t≥2,p≥5),pq(q>p≥5),

则

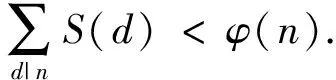
证明若n=pt(t≥2,p≥5),则由

2p<1+3p<(p-1)p=φ(p2),

以及引理2.3可知

若n=pq(q>p≥5),则由

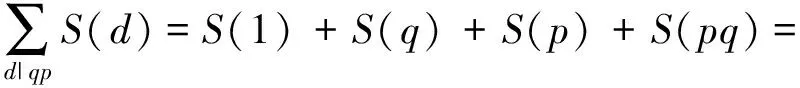
1+p+q+q≤3q-1<

(q-1)(p-1)-2=φ(qp)-2,

可知

若n=3t(t≥4),则由

28<54=φ(34),

以及引理2.3可得

若n=2t(t≥7),注意到

φ(2t)=2t-1.

不妨设

u(t)=φ(2

则

u(7)>0,u′(t)=2t-1ln2-2t-1,

u′(7)>0,u(2)(t)=2t-1ln22-2>0.

故当t≥7时,u(t)>0,所以

若n=2t3s(t≥7,s≥1),断言

为证明断言只需证明

因为

且

2t-1-(4+t+t2)=u(t)>0.

综上,断言得证.由上述断言以及引理2.3可得

这就完成了引理2.4的证明.

证明设

则n=n1n2且

n2(-1)

这就完成了引理2.5的证明.

引理 2.6设α≥2为正整数,p、q均为素数且q>p≥5,则:

1) (p-1)2pα-2>pα+2;

2) (q-2)(p-2)>q+2.

证明1)α=2,3,4,直接计算可知

(p-1)2pα-2>pα+2.

若α≥5,不妨设

v(α)=(p-1)2pα-2-pα-2,

则

v′(α)=(p-1)2ln(α-2)pα-2-p>0,

因而v(α)严格单调递增.又v(5)>0,故v(α)>0,即(p-1)2pα-2>pα+2成立.

2) 由q>p≥5可知

(q-2)(p-2)-q-2=qp-2q-2p-

q+2≥qp-5q+6>0,

即

(q-2)(p-2)>q+2.

这就完成了引理2.6的证明.

3 主要结果的证明

注意到

N+-{1}={n|p(n)≥5}∪{n|p(n)=3}∪

{n|p(n)=2且3⫮n}∪{n|p(n)=2且3|n},

故有以下4种情形:

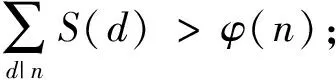
m∈{pt(p≥5,t≥2),pq(q>p≥5)},

m∈{33p,32p(p≥7),32×52,3p2}

A1={2t,t≤6},

A2={24p(p=5,7),23p,22×52}∪

{22p,2p2(p=5,7),2p},

A3={22×5p(p=7,11,13),2×7×11,2×5p},

且ω(Ai)=i,1≤i≤3;否则,存在正整数m|n,其中

m∈{2t|n,t≥7}

且ω(m)=1,或者

m∈{26p,25p,24p(p≥11),24p2(p=5,7),23p2}∪

{22p2(p≥7),22×53,2p2(p≥11),

2p3(p=5,7)}

且ω(m)=2;或者

m∈{24pq(p=5,7),23pq,22×52p,22pq2}∪

{22pq(p≥7),22×5p(p≥17),

2p2q(p=5,7)}∪

{2pq2,2pq(p≥11),2×7p(p≥13)},

且ω(m)=3,其中q>p;或者

m∈{22×5pq(q>p=7,11,13),

2×7×11p,2×5pq},

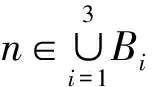
B1={34×2,33×2t(t≤3),32×2t(t≤4)}∪

{3×2t(t≤6)},

B2={33×2×5,32×23×5,32×2p}∪

{32×22p(p=5,7,11,13),3×25×5}∪

{3×23p,3×24p(p=5,7),3×22×52}∪

{3×22p,3×2p2(p=5,7),3×2p},

B3={3×22×5p(p=7,11,13)}∪

{3×2×7×11,2×3×5p},

且

ω(Bi)=i+1, 1≤i≤3;

否则,存在正整数m|n,其中

m∈{2t3s(t≥7,s≥1),2i×32(i=6,5)}∪

{24×33,2i×34(i=2,3),2×35}

且ω(m)=2;或者

m∈{34×2p,33×2ip(i=2,3)}∪

{33×2p(p≥7),33×2×52,32×24p}∪

{32×23p(p≥7),32×23×52,32×22p2}∪

{32×22p(p≥17),3×23p2,32×2p2}∪

{3×25p2,3×25p(p≥7),3×25×52}∪

{3×24p(p≥11),3×24p2(p=5,7)}∪

{3×2p2(p≥11),3×2p3(p=5,7)}∪

{3×22×53,3×22p2(p≥7)},

且ω(m)=3;或者

m∈{q(B2-{3×22p,3×22pq2})}∪

{3×22pq(p≥7),3×22×5q(q≥17)}∪

{3×2p,3×2pq2,3×2pq(p≥11)}∪

{3×2×7q(q≥13)},

且ω(m)=4,其中q>p;或者

m∈{3×22×5pq(q>p=7,11,13)∪

{3×2×7×11p,3×2×5pq},

推论1.2的证明直接计算可知

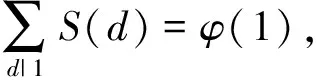
再由定理1.1立得结论.

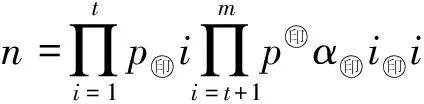
S(n)=S(pα)=max{S(pi)(i=1,2,…,t),

S(pαii)(i=t+1,t+2,…,m)},

以及

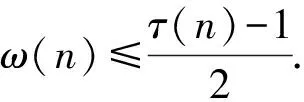
以及

故由引理2.6可知,当d≠1,p时,有

因此

S(d2ω(n)+2)+…+S(dτ(n))=S(1)+

S(d2ω(n)+2)+…+S(dτ(n))<

f(d2ω(n)+2)+…+f(dτ(n))=

φ(n)-(2τ(n)-4ω(n)-2).

这就完成了定理1.3的证明.

4 一些例子

本小节给出几个例子进一步验证本文的主要结果.

2)n=17 640.一方面,因为n=17 640=23×32×5×72,3|n,p(n)=2,ω(n)=4,n∉B3,所以

另一方面,因为

另一方面,有

S(2p)+S(3p)+S(6p)+S(q)+S(2q)+

S(3q)+S(6q)+S(pq)+S(2pq)+S(3pq)+

S(6pq)+S(γ)+S(2γ)+S(3γ)+S(6γ)+

S(pγ)+S(2pγ)+S(3pγ)+S(6pγ)+S(qγ)+

S(2qγ)+S(3qγ)+S(6qγ)+S(pqγ)+

S(2pqγ)+S(3pqγ)+S(6pqγ)=

9+4p+8q+16γ<48γ-48≤

2(p-1)(q-1)(γ-1)=φ(6pqγ),