一种几何非线性复合材料梁瞬态动响应计算方法*

张勇 霍佳波 宋小辉 张凌云

(桂林航天工业学院 机电工程学院，广西 桂林 541004)

先进的复合材料具有高比强度、高比模量、优越的抗疲劳和耐环境等性能，在航空、航天、船舶、车辆等领域取得了广泛的应用[1]。高长细比复合材料梁在航空航天领域、汽车领域有着广泛的用途，比如直升机旋翼叶片、飞机机翼大梁、汽车减振板簧等。细长梁结构在受载状态下，往往表现出几何非线性变形的特征。复合材料因为存在各向异性，在变形过程中，还存在拉伸、弯曲、扭转多自由度之间的耦合以及与截面翘曲变形的复杂耦合效应。另外，作为结构的主承力梁，往往面临突加载荷的作用。因此对复合材料中等变形梁进行瞬态响应研究，可充分发挥复合材料结构的可设计性，对复合材料梁结构设计有着重要的意义。

几何非线性中等变形梁模型主要由Hodges等人完成的。1974年，Hodges和Dowell提出了中等变形梁模型，推导过程中使用阶次准则忽略那些由于中等变形引起的高阶项，最终给出适应于均匀的、各向同性的挥-摆-扭耦合的非线性桨叶运动方程[2]。随后，Tong、Kaza等人进一步发展和扩充了中等变形梁理论，考虑了结构挥-摆-扭耦合以及预扭、预锥等。1985年，Hodges舍弃了中等变形假设，建立了另一套考虑了剪切变形、弹性轴初始弯曲和预扭的弯扭耦合旋翼桨叶运动方程，即小应变有限转角旋转梁理论。随后为了使建立的模型适用于复合材料桨叶[3]，1990年，Hodges没有再限制弹性转角的大小，并且采用非传统的截面三维翘曲的概念，进一步发展了有限转角旋转梁理论[4]。2008年，王益峰[5]等人建立了一种复合材料柔性梁静态响应计算方法，采用中等变形梁理论，对梁结构进行了有限元分析。动响应常用的求解方法是模态叠加法，但是模态叠加法无法准确计算高阶模态。近年来，国内外学者提出了通过直接的非线性数值积分求解旋翼结构动响应的方法，主要方法有线性加速度法、Newmark法、Wilson-θ法、HHT(Hilber-Hughes-Taylor)法等。2018年，电子科技大学的石胜兵[6]将时域微分方程数值积分的经典时域步进算法——Newmark 算法引入到时域有限差分法中，利用中心差分离散空间偏微分，得到了一种基于Newmark算法的无条件稳定的时域有限差分法，并将算法引入电磁领域，证明了该算法有效性和高效性。文献调研表明，国内外学者对几何非线性中等变形梁理论及其静态响应进行了一定的研究，但是对瞬态动响应的研究较少。Newmark算法具有高稳定性和高精度的特点，对于求解中等变形梁的动响应问题具有较好的应用价值。

本文在Hodges中等变形非线性梁理论的基础上，运用VABS算法得出复合材料梁的剖面特性，然后结合有限元法，引入Newmark算法，开展中等变形非线性复合材料梁的瞬态动响应计算研究。以某飞机机翼翼梁算例，得到了翼梁在初始垂直速度下的位移、速度和加速度响应，并分析了附加集中质量位置对计算结果的影响。

1 复合材料梁剖面特性计算模型

1.1 局部坐标系与铺层角定义

针对复合材料层合结构，建立铺层局部坐标系，如图1所示，其中x为梁剖面的坐标系，e为沿材料主方向建立的坐标系，y为单层局部坐标系。定义θ1和θ3用于表征单层铺层角，其中θ3为材料主坐标系e与局部坐标系y的夹角，θ1是铺层坐标系x与单层局部坐标系y的夹角。

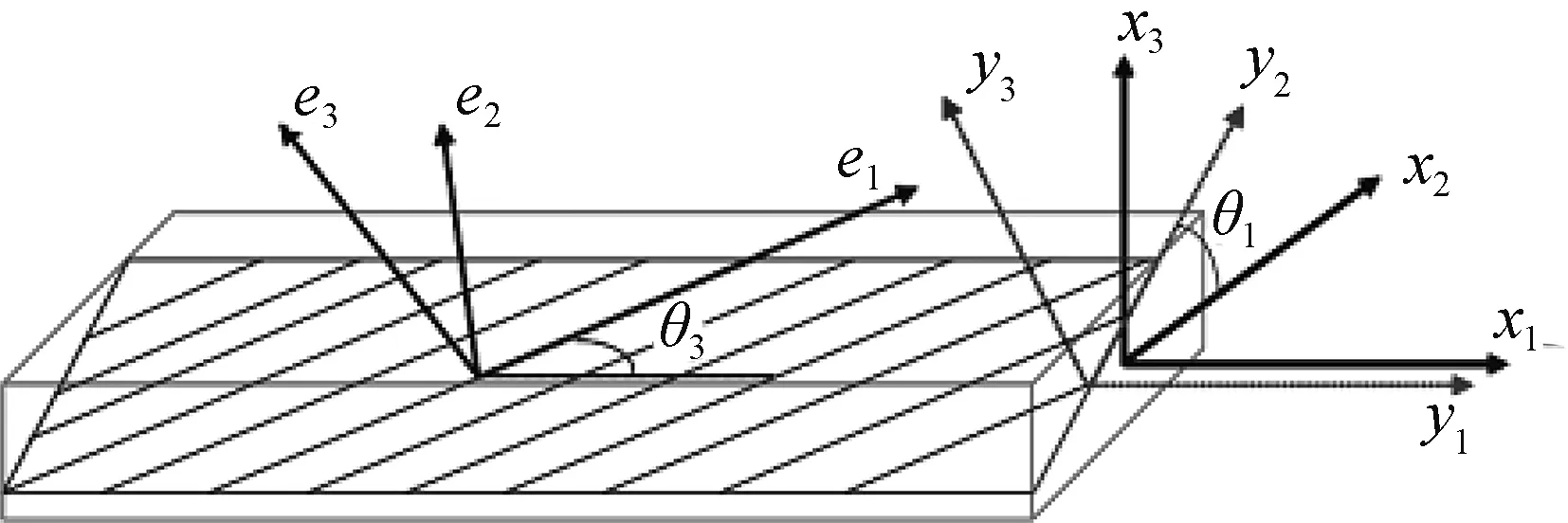
图1 复合材料铺层角度定义

1.2 剖面特性计算

对于简单形状的各向同性材料梁剖面，可以采用材料力学方法得到梁剖面的质量-刚度特性，而复合材料梁沿展向的剖面刚度特性和质量特性比较复杂，本文采用有限元的方法进行计算。

VABS[7]程序由Wenbin Yu等人研发，使用变分渐近数值方法能够计算具有任意几何和材料特性的梁的一维横截面刚度常数，并进行横向剪切和Vlasov细化，并通过多次试验验证了该程序的准确性[8]。本文基于Hypermesh软件和VABS程序，运用matlab软件进行文本处理，最终建立了一套剖面特性计算方法，剖面特性计算流程如图2所示。

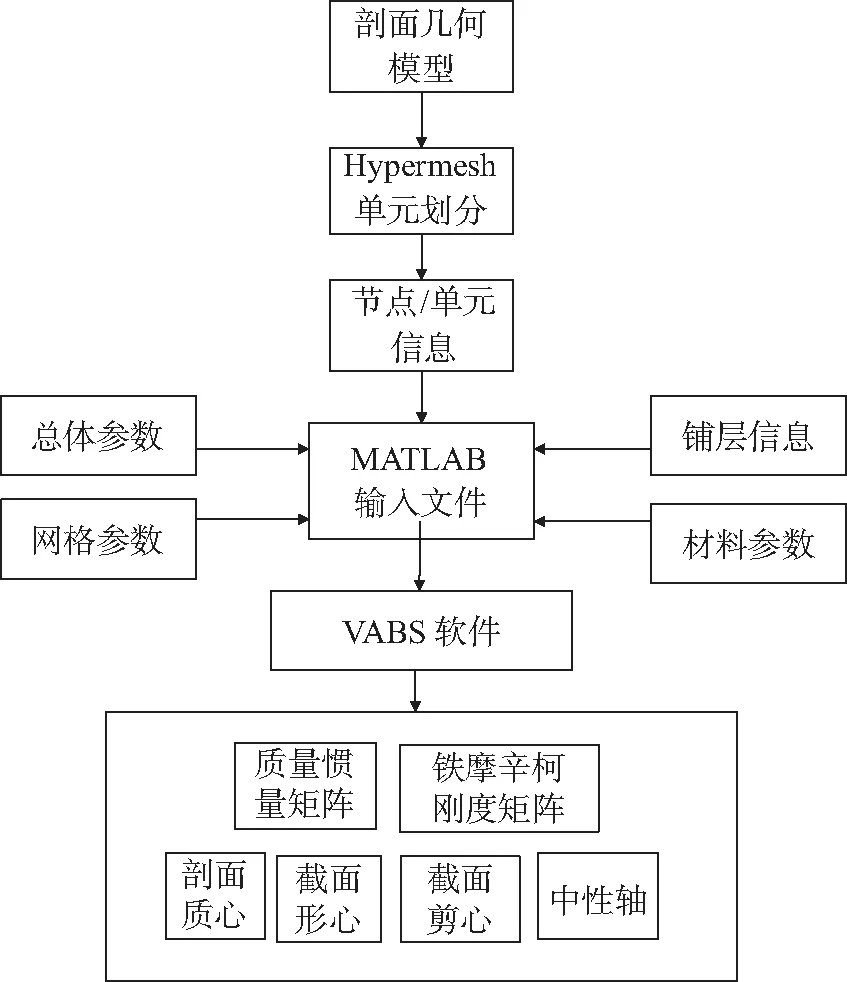
图2 基于Hypermesh-VABS的剖面参数计算流程图

2 几何非线性梁模型

2.1 坐标系及几何非线性变形模型

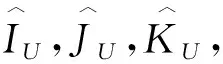
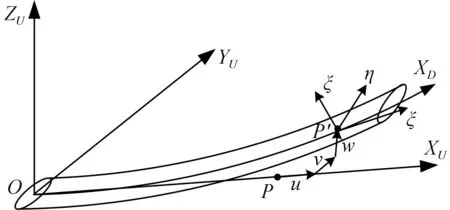
图3 梁单元变形坐标系

未变形坐标系和变形坐标系下，单位向量的转换关系为：

(1)

(2)

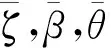
(3)

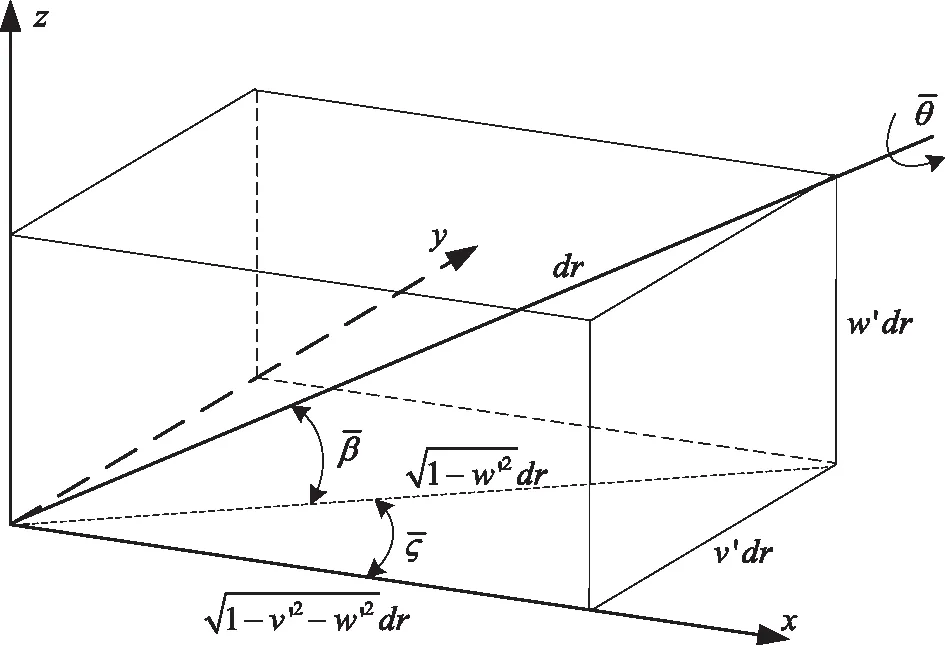
图4 欧拉角几何关系示意图

根据欧拉角变换关系，考虑梁在拉伸、弯曲、扭转方向的耦合变形关系以及几何变形非线性，将TDU简化到保留二阶小量，可得式(4)。

(4)

2.2 汉密尔顿方程

对于非保守系统，汉密尔顿作用量的表达式为：

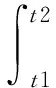
(5)

其中：δU、δT和δW分别表示应变能变分、动能变分和外力虚功变分，并且各个变分项由各单元的变分叠加得到，即：

其中：N表示单元总数；δUi、δTi和δWi分别表示第i个梁单元的应变能变分、动能变分和外力虚功变分。

2.2.1 应变能变分

保留二阶小量的几何非线性梁模型的正应变和切应变表达式如下：

(6)

进而可推导第i个梁单元的应变能变分：

(7)

其中式(7)中，各变量表达式如下：

式中：EA表示梁的轴向拉伸刚度；EIy表示梁绕z轴的弯曲刚度；EIz表示梁绕y轴的弯曲刚度；GJ表示梁的扭转刚度。其中包含“︿”的量表示与剖面的翘曲有关。

2.2.2 动能变分

在未变形坐标系中，选取未变形梁单元上任意一点P(x,0,0)，发生变形后移动到了p′(x+u,v,w)，并且包含该点的剖面相对于变形后弹性轴旋转了θ1。

梁单元上任意一点关于左侧节点的速度可表达如式(8)。

(8)

速度及速度的变分表达式为：

(9)

(10)

第i个梁单元的动能表达式和动能变分表达式分别为：

(11)

(12)

其中：ρs表示梁的线密度。

将式(9)及式(10)代入动能变分表达式(12)中，然后通过分部积分得到动能变分表达式为：

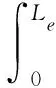
(13)

其中：

(14)

进一步，将动能变分表达式写成关于六个自由度的表达形式，可得：

Tv′δv′+Tw′δw′+Tφδφ+TF)dx

(15)

其中：

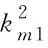
2.2.3 外力虚功变分

针对本文求解的瞬态动响应问题，单元外力计入单元体力和节点六力素，可得外力虚功变分为：

(16)

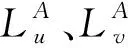
2.3 有限元模型

2.3.1 单元离散

如图5所示，选用2节点12自由度梁单元模型对复合材料梁进行单元离散，每个节点包含6个自由度，分别为拉伸位移u，沿z轴的位移v，绕y轴的转角v′，沿y轴的位移w，绕z轴的转角w′，绕x轴的扭转角φ。

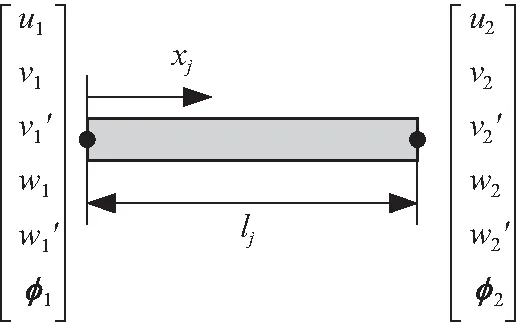
图5 2节点12自由度梁单元模型

单元节点的位移向量为：

(17)

单元形函数采用非线性插值，节点位移到单元位移的换算关系如式(18)。

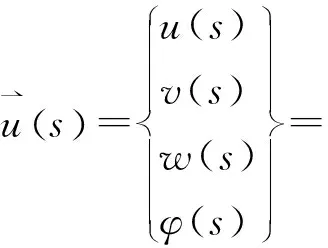
(18)

其中：

Hu1=Hφ1=1-s

Hu2=Hφ2=s

Hv1=Hw1=2s3-3s2+1

Hv1′=Hw1′=li(s3-2s2+s)

Hv2=Hw2=-2s3+3s2

Hv2′=Hw2′=li(s3-s2)

s=xj/lj

根据汉密尔顿原理，将单元形函数和节点位移向量带入，可得单元的汉密尔顿作用量为：

(19)

其中：[M]j表示第j个单元的质量矩阵，[C]j表示第j个单元的阻尼矩阵，[K]j表示第j个单元的刚度矩阵。

2.3.2 结构阻尼模型

几何非线性梁振动过程中，起动能耗散作用的因素主要是结构阻尼。结构阻尼是指机械系统振动时，其内部产生交变的应变，通过材料内摩擦而消耗能力，是反映结构体系振动过程中能量耗散特征的参数。结构振动时耗能因素较多，但影响程度有所不同。文献[10]中提出了四种阻尼模型的建模方法，分别为总体Rayleigh阻尼法，单元Rayleigh阻尼法，整体阻尼比法，单元阻尼比法。对于复合材料梁，各单元段铺层可能存在差异，本文选择单元Rayleigh阻尼模型。

Rayleigh阻尼用于单一阻尼特性的简单阻尼结构体系中，各部分阻尼可用统一的阻尼参数代表，此种结构中，取阻尼c=αm+βk，其中，α，β通过式(20)确定。

(20)

其中：ξm，ξn为给定两个典型模态振型的阻尼比，工程应用和研究中，可以通过模态试验测得。

2.3.3 矩阵组装

按照有限元法，依据各单元间的公共节点关系组装各个单元便可获得总质量矩阵、总阻尼矩阵、总刚度矩阵和总载荷向量。依据汉密尔顿原理，将总体质量、阻尼和刚度矩阵带入，便可得到整个复合材料梁的汉密尔顿作用量表达式：

(21)

由于实际的位移向量δqT为任意量，所以式(21)可以转化为如下的有限元形式的复合材料梁运动方程：

(22)

其中：M为梁的总体质量矩阵，C为梁的总体阻尼矩阵，K为梁的总体刚度矩阵，F为梁的外载荷总向量。

3 瞬态动响应求解模型

本文采用Newmark方法对时间进行离散，得到复合材料梁的时域有限元方法。基于Newmark法的位移、速度、加速度满足以下条件：

(23)

将公式(23)的第三式代入前两式，可得：

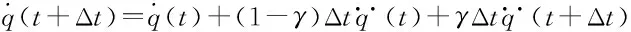
(24)

将公式(24)进一步改写成:

(25)

(26)

其中：

b4=γb1Δt,b5=1+γb2Δt,b6=(1+γb3-γ)Δt

(27)

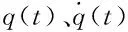
γ和β为Newmark算法参数，γ∈[0,1]，β∈[0,0.5]其中当γ≥0.5，β≥0.25(0.5+γ2)时，Newmark法是无条件稳定的，所以本文的Newmark参数取γ=0.5，β=0.25。

基于Newmark法的复合材料梁瞬态动响应计算流程如图6所示。

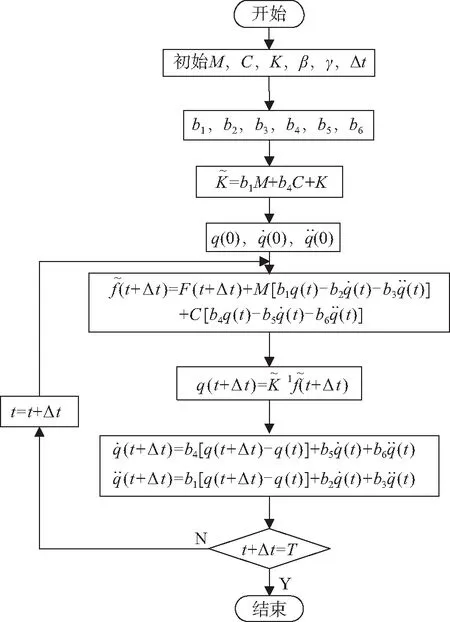
图6 Newmark瞬态动响应计算流程

4 算例计算及讨论

以变截面混杂复合材料机翼盒型曲梁作为算例，玻璃纤维和碳纤维均为预浸编织布，翼梁铺层角为[(0/90)G/(0/90)C/(±45)G/(±45)C/(0/90)G]，翼梁根部剖面几何尺寸如图7所示。翼梁长度为2 m，无上反，沿抛物线曲线后掠，梁轴线函数为y=0.1x2，翼梁剖面梢根比为0.5，翼梁几何模型如图8所示。复合材料参数摘自文献[11]。

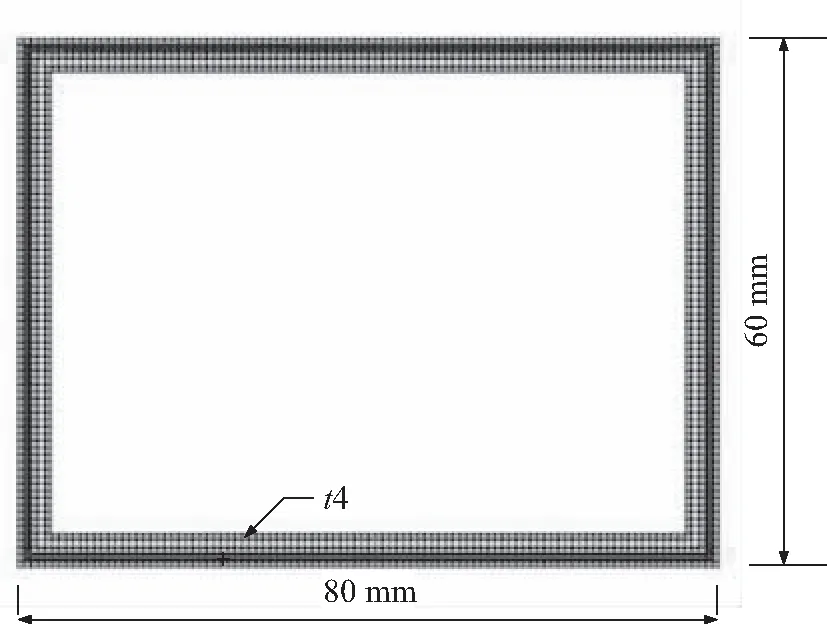
图7 算例复合材料曲梁根部剖面示意图

图8 算例复合材料曲梁三维模型

算例工况：初始垂向速度瞬态响应分析，模拟飞机在应急着陆过程中垂直下降率过大的工况。

本文计算下降率2 m/s工况下翼梁0.6 s内的瞬态动响应，算得振动响应时间为0.493 5 s。翼尖节点加速度、速度、加速度响应如图9～图11所示，响应过程中翼尖最大位移为0.031 6 m，最大速度为4.441 m/s，最大加速度为1 561.4 m/s2。分析图像可以看出，0～0.12 s内响应位移较大，响应曲线表现出较强的非线性特征；0.12～0.6 s内位移值较少，曲线特征为标准的正弦衰减曲线。

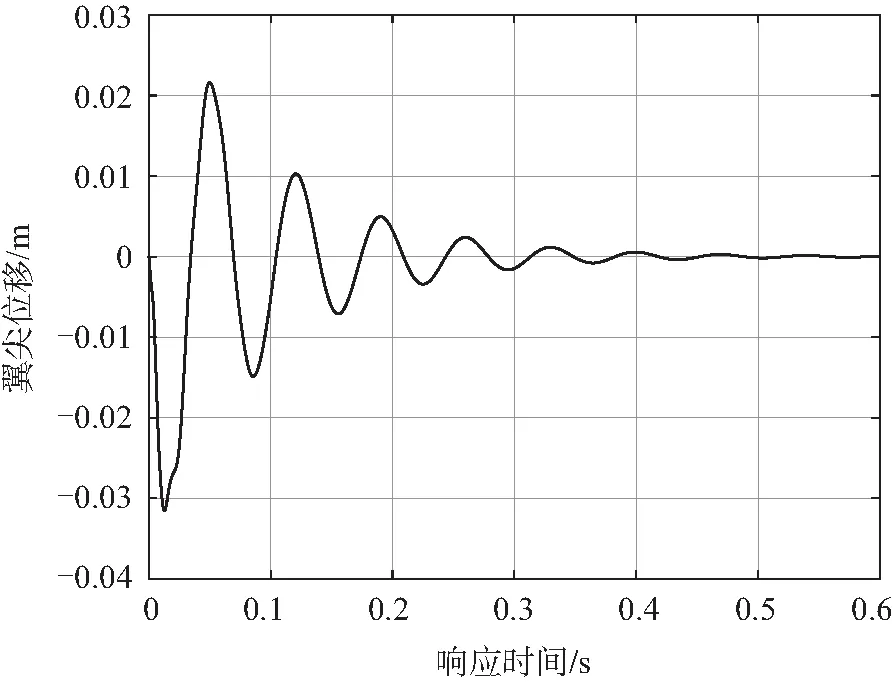
图9 2 m/s下降率着陆0～0.6 s翼尖位移响应曲线

图10 2 m/s下降率着陆0～0.6 s翼尖速度响应曲线

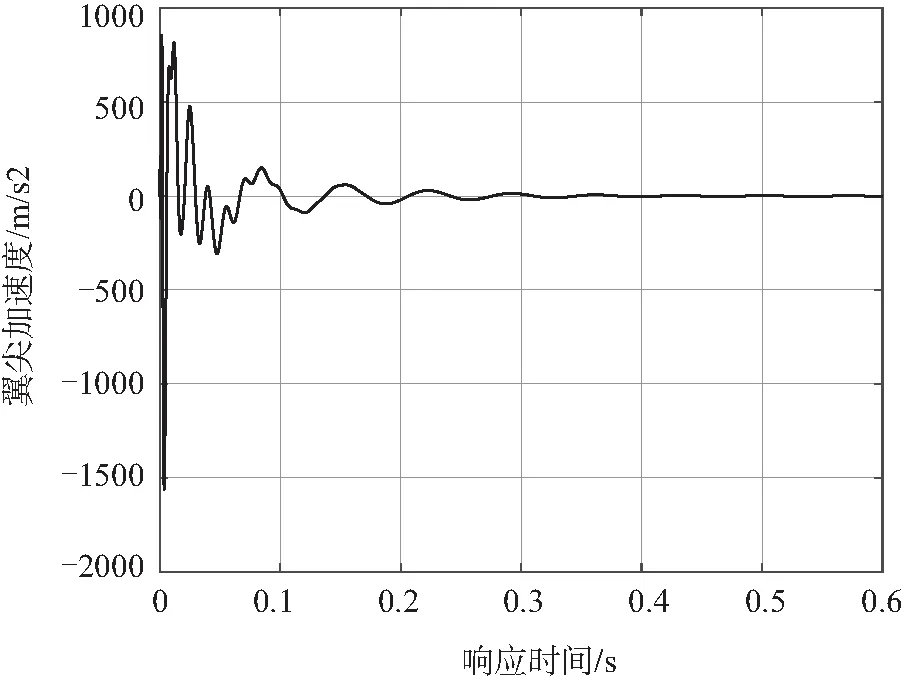
图11 2 m/s下降率着陆0～0.6 s翼尖加速度响应曲线

在飞机机翼上，会有发动机、副油箱等集中质量挂载点。本文在计算过程中考虑翼梁有附加集中质量地对着陆响应的影响，分别在机翼根部、中部和翼尖位置附加1 kg的集中载荷，初始动能相同的情况下，计算得到机翼翼尖位移、速度和加速度动响应如图12～图14所示。

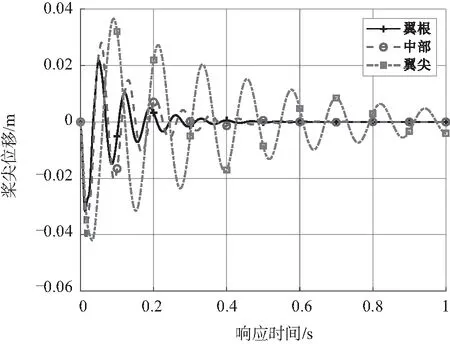
图12 附加集中质量位置对位移响应的影响

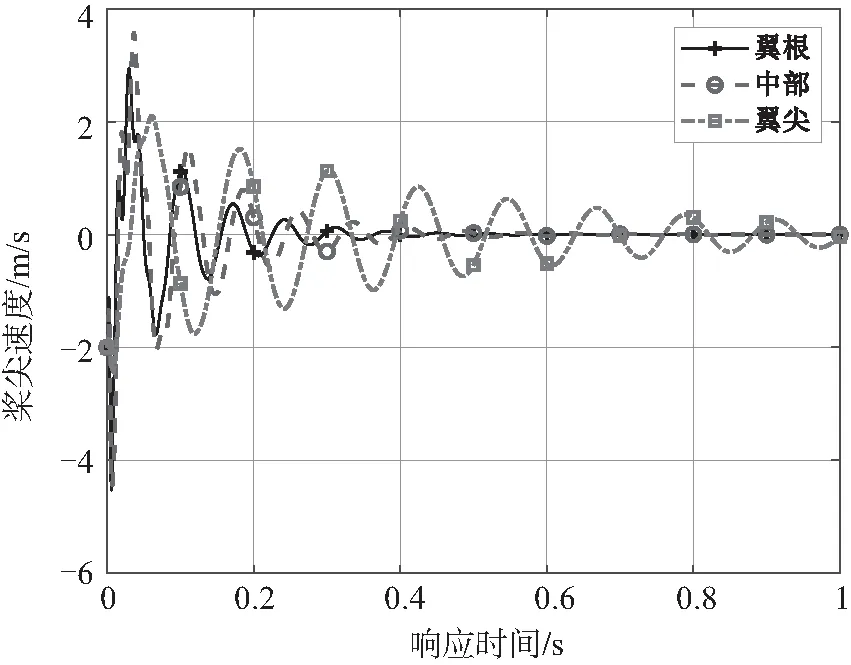
图13 附加集中质量位置对速度响应的影响

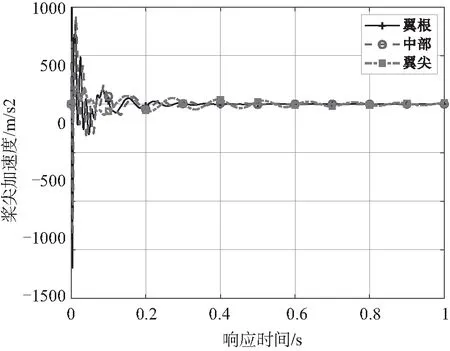
图14 附加集中质量位置对加速度响应的影响

计算得到三种状态下的动能耗散时间、翼尖最大垂向位移、最大垂向速度和最大垂向加速度如表1所示。计算结果表明，附加质量越靠近翼尖， 动能耗散时间越长，阻尼振动响应周期越长，翼尖最大垂向位移响应越大，翼尖最大垂向速度越小，翼尖最大垂向加速度越小。

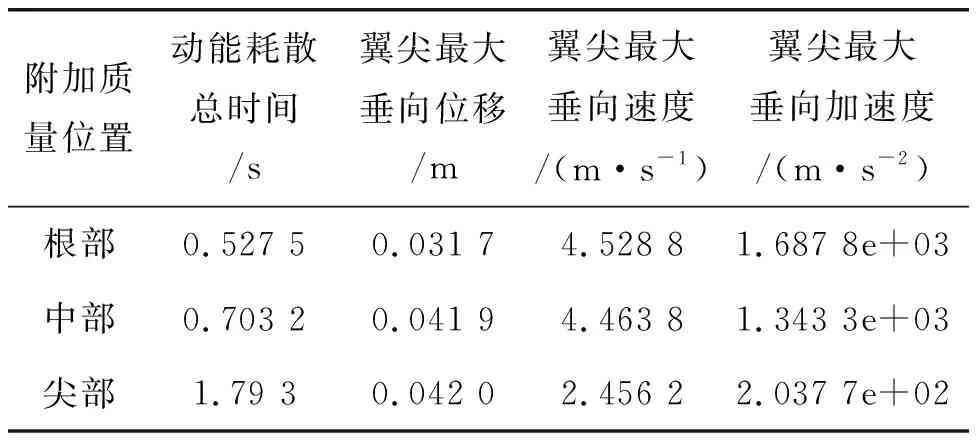
表1 附加集中质量位置对振动响应的影响结果汇总

根据表1中的数据，分析附加质量位置对动能耗散总时间和翼尖最大垂向位移两个关键参数的影响，如图15所示。可以看出，动能耗散总时间和翼尖最大垂向位移均随着附加质量的展向位置的增加而单调增加，将集中质量布置在翼根对降低动响应时间和位移幅值最有利。对比翼根和翼中附加质量的计算结果，翼尖最大垂向位移增加了32.18%，动能耗散时间增加了33.31%；对比翼中和翼尖附加质量的计算结果，翼尖最大垂向位移增加了154.98%，动能耗散时间增加了0.24%。

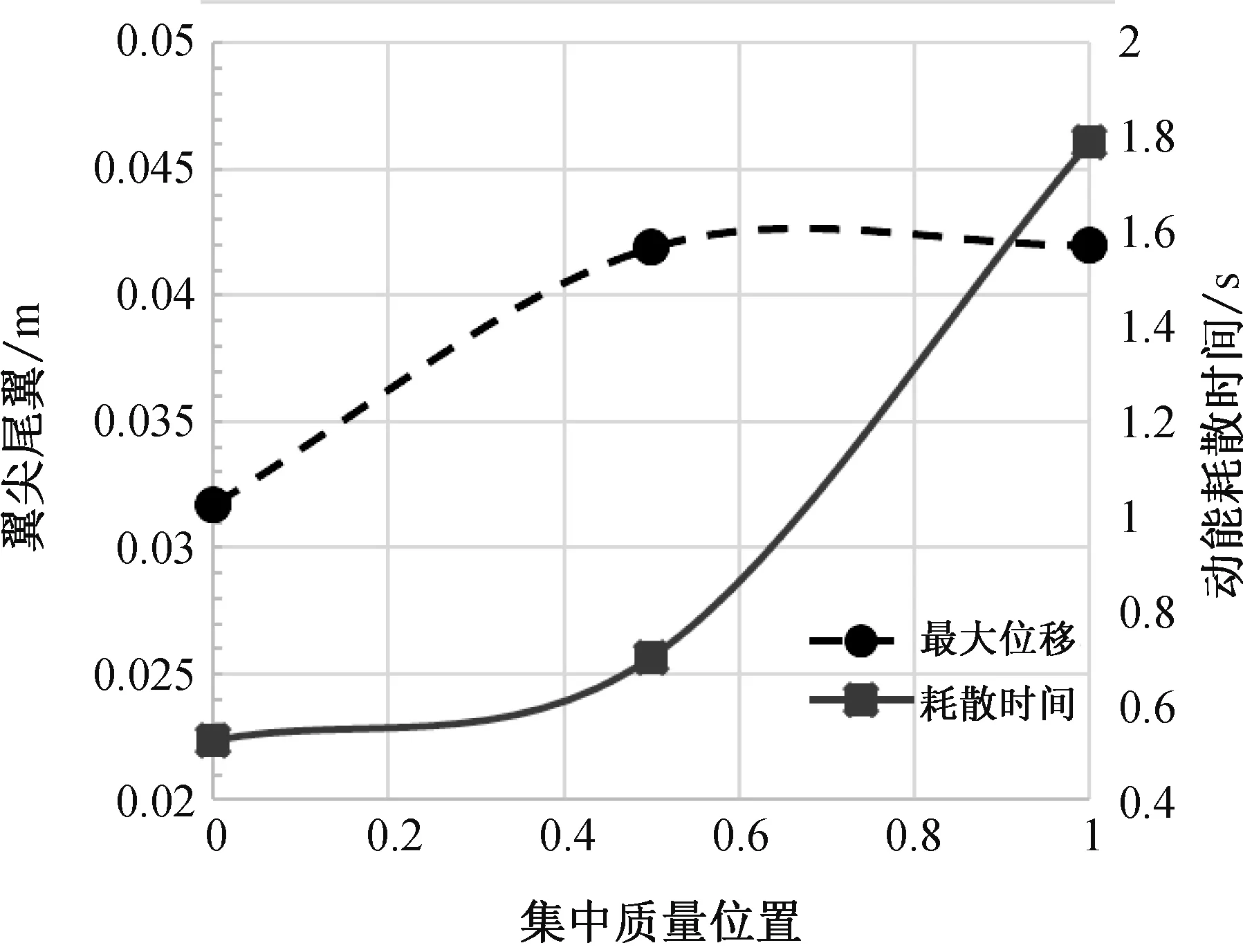
图15 附加质量位置对最大位移和耗散时间的影响对比

5 总结

本文将高长细比复合材料梁分解成非线性一维梁模型和线性二维剖面特性分析两部分，首先根据梁剖面的几何特性和铺层特征，运用VABS算法得出梁剖面的质量矩阵、刚度矩阵等，然后将基于Hodges中等变形梁模型，建立中等变形梁模型，将二维剖面特性参数带入梁模型中。选用Newmark算法，完成一套基于VABS程序、Hodges中等变形梁模型和Newmark算法的几何非线性复合材料梁瞬态动响应高效计算方法。最后以某飞机机翼翼梁为算例，得到了翼梁在初始垂直速度下的位移、速度和加速度响应，并分析了附加集中质量位置对计算结果的影响。

在工程应用中，复合材料主承力梁的结构设计思路往往是从二维剖面设计再到三维结构设计，且初步设计阶段并未将动响应考虑在内。本文所研究的算法具有高效性和高精度性，对考虑动响应的复合材料梁的高效优化迭代设计具有一定的应用前景。通过对飞机机翼大梁响应进行算例分析，得出了以下结论：

1)中等变形复合材料梁在初始响应阶段，由于梁挠度较大，在位移、速度、加速度时域曲线中，表现出典型的几何非线性响应特性。

2)中等变形复合材料梁在响应稳定衰减阶段，梁挠度变小，中等变形梁退化为小变形梁动响应问题，位移、速度、加速度时域曲线为标准正弦衰减型号。

3)附加集中质量位置对复合材料中等变形梁的动响应指标参数均有不同程度的影响，本文的研究内容可用于指导结构方案布局设计。