基于连续-非连续单元法的三维脆性颗粒冲击破碎特性分析

刘新明， 冯 春*， 林钦栋

(1.中国科学院 力学研究所，北京 100190；2.中国科学院大学 工程科学学院，北京 100049；3.西安近代化学研究所，西安 710065)

1 引 言

冲击载荷下脆性颗粒的破碎特性一直都是破碎领域中重点关注的研究内容。颗粒破碎的主要演化阶段为微裂纹萌生、扩展、贯通直至形成宏观裂缝，整个过程历时极短且速度极快，常规监测手段难以对其损伤破碎演化过程进行精准描述。因此数值模拟已经成为解决冲击破碎和材料断裂等复杂问题的有效手段，其中离散元法(DEM)和有限离散元耦合法(FDEM和CDEM等)是模拟脆性材料破碎的两种主要数值算法。

离散元法是Cundall[1]提出的非连续变形数值方法。该方法适用于描述颗粒的非连续变形问题，在众多学科和工程领域有着极为广泛的应用[2]。Cil等[3]采用离散元法验证了土基颗粒整体压碎的宏观能量与单个颗粒受拉断裂的宏观能量之间的标度律的有效性。Xu等[4]使用BPM模型将载荷施加在黏结为颗粒簇的单元上，分析了颗粒破碎时的力学特性。文献[5-7]基于离散元法进行了球形颗粒撞击靶体及两球形颗粒撞击破碎的相关数值分析，探讨了撞击速度和接触面积的大小对破碎行为的影响。脆性岩石材料在静载与动载的作用下强度特征差异很大，是一种典型的应变率敏感材料，因此研究冲击载荷下脆性颗粒的破碎特性及动态响应对尚在发展的动态强度理论是十分有意义的。

由于离散元法难以对颗粒本身细观力学特性进行精确的描述，因此在进行细观数值模拟时很难定量体现颗粒材料的宏细观力学属性。因此有限离散元耦合的相关数值方法应运而生。文献[8-10]发展了FDEM方法。Guo等[11]基于FDEM方法建立了准脆性材料的三维裂纹扩展模型，并进行了网格无关性分析和裂纹扩展正确性的算例验证。Ma等[12-15]利用FDEM方法和计算机断层扫描技术对不规则颗粒的冲击破碎和压碎进行了模拟，分析了颗粒形状对破碎效果的影响及在冲击荷载下的破碎临界特性和碎片分形特性。李世海等[16]建立并发展了CDEM方法。王杰等[17]基于CDEM方法对岩石单轴压缩破坏的过程进行模拟，描述了裂纹在拉伸和压剪等不同应力状态下的扩展问题,同时极大地提升了计算效率。冯春等[18]基于CDEM方法实现了外加载荷下岩体损伤破裂过程的模拟，探讨了数值试样的应变率效应。Lin等[19]基于CDEM方法提出了黏聚性断裂模型，解释了裂纹萌生和扩展过程的能量耗散现象。由于CDEM方法能够很好地模拟脆性材料在动载作用下的连续变形、裂缝扩展及破碎后运动碰撞，并且对破碎过程中的能量转化有着良好的定量化描述方法，因此十分适用于研究冲击载荷下脆性颗粒的破裂破碎问题。

本文以典型脆性材料岩石颗粒为例，采用连续-非连续单元法(CDEM)，以描述脆性颗粒损伤、断裂和破碎的关系，从而详细讨论破碎状态与冲击速度的关系及破碎过程中的能量演化规律。

2 脆性颗粒本构模型及能量统计算法

2.1 脆性颗粒断裂能本构模型

采用连续-非连续单元法研究三维球体脆性岩石颗粒在不同冲击速度下的破坏特性。连续-非连续单元法是通过拉格朗日能量系统建立严格的控制方程，利用动态松弛法显式迭代求解，从而实现连续-非连续的统一描述，通过块体边界及块体内部的断裂来分析材料渐进破坏，可模拟材料从连续变形到断裂直至运动的全过程。如图1所示，CDEM的数值模型由块体及界面两部分构成。

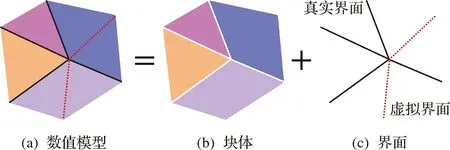
图1 CDEM的数值模型构成

CDEM对于动力问题的解答包含两个步骤，即在每一步中分别对有限元和离散元进行求解，系统的整体受力情况通过不平衡率来表述，全部计算均使用了基于增量方式的显式欧拉前差法，控制式是质点运动方程。

CDEM中单元的本构方程为

(1)

式中σi j为应力张量,Δσi j为应力张量增量,Δεi j为应变张量增量,Δθ为体应变增量,K为体积模量,G为剪切模量,δi j为Kronecker记号,t0为当前时步,t1为下一时步。

采用增量法计算虚拟界面上下一时步的法向及切向试探接触力，

(2)

式中Fn和Fs为法向和切向接触力，Kn和Ks为单面面积上法向和切向接触刚度(单位：Pa/m)，Ac为虚拟界面的面积，Δdun和Δdus为法向和切向相对位移增量。

采用式(3)进行拉伸破坏的判断、法向接触力及抗拉强度的修正，为

(3)

式中σt 0，σt(t0)和σt(t1)为初始时刻、本时刻及下一时刻虚拟界面上的抗拉强度，Δun为当前时刻虚拟界面上的法向相对位移，Gf t为拉伸断裂能(单位：Pa·m)。

采用式(4)进行剪切破坏的判断、切向接触力及粘聚力的修正，

(4)

当考虑应变率的影响时，初始粘聚力及初始抗拉强度与应变率之间的函数关系为

(5)

2.2 颗粒脆性破坏能量统计算法

为了准确研究脆性颗粒渐进破坏过程中模型的能量演化规律，使用相关能量统计方法[20]。如图2所示，主要统计以下6种能量,即块体在外部荷载作用下的变形能和动能，界面两侧的块体发生相对运动时，界面上数值弹簧的拉伸变形能和剪切变形能，以及单元相互作用过程中的摩擦耗能和阻尼耗能。

图2 能量统计方法

单元变形能WE E为

(6)

式中NE为模型中单元的总个数，we e为单元的弹性变形能密度，we p为塑性变形能密度，vk为单元的体积。

单元动能WE V为

(7)

式中ve x，ve y和ve z为单元体心的速度在全局坐标系X，Y和Z方向的分量，mk为单元的质量。

界面处弹簧变形能WP E为

(8，9)

式中wp et为拉伸变形能，wp es为剪切变形能，wp e为单个弹簧的变形能，Np为模型中弹簧的总数量。

弹簧的断裂能分为拉伸断裂能和剪切断裂能，首先根据每个弹簧的破坏类型求出单个弹簧的断裂能wp c(式(10))；随后，遍历所有发生破断的弹簧，求出所有破断弹簧的断裂能累积值WP C(式(11))。弹簧断裂能WP C为

(10，11)

式中wp c为单个弹簧的断裂能,如果发生拉伸破坏，wp c等于拉伸断裂能wp t与剪切断裂能wp s之和，如果发生剪切破坏，wp c等于剪切断裂能wp s,NP C为已发生破断的弹簧数量。

t时刻到t+Δt时刻界面两侧单元的相对摩擦位移ΔUi(即ΔUx和ΔUy)的表达式为

(12)

根据上述分析，摩擦耗能WR的计算公式为

(13，14)

阻尼耗能WR的统计算法为

(15)

式中No为模型中节点的数量，Fo x,Fo y和Fo z为节点的合力在全局坐标系X，Y和Z方向的分量，ΔUo x，ΔUo y和ΔUo z为t时刻至t+Δt时刻节点的位移增量在全局坐标系X，Y和Z方向的分量。

2.3 颗粒破碎程度的评价指标

颗粒的破坏发生在单元的虚拟界面间。虚拟界面的主要作用是为显式裂纹的扩展提供潜在的通道，即裂纹可沿着任意一个虚拟界面进行扩展。为定量描述颗粒冲击破碎后的破坏程度与破裂状态，引入破裂度Df、损伤度Dd及平均损伤因子FA。

破裂度Df是指已破裂单元的虚拟界面面积除以可破裂的虚拟界面总面积，可表示为

Df=Sb/ST

(16)

式中Df为破裂度，Sb为已破裂单元的虚拟界面面积，ST为可破裂的虚拟界面总面积。

损伤度Dd是指对已破裂单元的虚拟界面面积乘以对应虚拟界面上的损伤因子进行累计求和，再除以可破裂的虚拟界面总面积。其表达式如下，

Df=∑Sb·Fd/ST

(17)

式中Df为破裂度，Sb为已破裂单元的虚拟界面面积，Fd为对应虚拟界面上的损伤因子，ST为可破裂的虚拟界面总面积。

颗粒破碎后会生成若干新块体，平均损伤因子FA用于表征新生成块体的平均损伤程度。其计算流程为先求出各个新块体的损伤度，再计算所有新块体损伤度的平均值，可表示为

(18，19)

式中FA i为新生成的第i个块体的平均损伤因子，Sb i为新生成的第i个块体的破裂面积，ST i为新生成的第i个块体的界面总面积，FA为平均损伤因子，N为新生成块体的总数。

在CDEM计算方法中，平均损伤因子FA分为平均拉伸损伤因子FA T与平均剪切损伤因子FA C单独进行计算，可表示为

FA T=1-σt/σt(0),FA C=1-C/C(0)

(20，21)

式中FA T为平均拉伸损伤因子，σt为当前时刻的拉伸应力，σt (0)为界面的抗拉强度，FA C为平均剪切损伤因子，C为当前时刻的内聚力，C0为界面的内聚力。

3 脆性颗粒数值模型与计算参数

3.1 脆性颗粒数值模型

如图3所示，建立三维球体脆性岩石颗粒模型的数值模型和网格模型。该颗粒模型的直径为 10 mm，采用四面体单元，共划分了79901个网格。表1为颗粒试样的物理力学性质。该数值模型为典型的脆性岩石颗粒性质。本文分别对颗粒模型进行了冲击速度为25 m/s,50 m/s,75 m/s,100 m/s,125 m/s和150 m/s的冲击模拟，对颗粒冲击刚性面发生破碎后的破碎块度、损伤程度和能量演化规律程度进行了研究分析。破碎块度是指颗粒在冲击刚性面发生破碎后新生成的独立块体的特征尺寸，可用于定量化描述冲击破碎后的破碎效果，如累计粒度分布百分数D50。

图3 三维脆性岩石颗粒试样的数值及网格模型

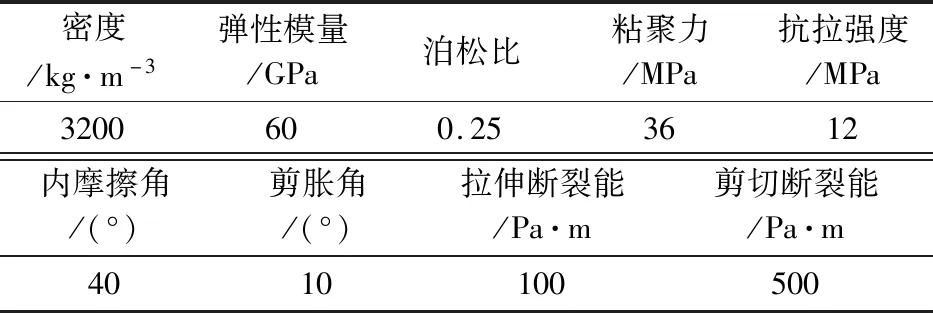
表1 三维脆性岩石颗粒试样数值模型的物理力学性质

3.2 脆性颗粒冲击破碎结果

在本次数值模拟实验中，共设置6种冲击速度，分别模拟25 m/s，50 m/s，75 m/s，100 m/s，120 m/s和150 m/s速度下三维颗粒的冲击破碎情况，共计算150.67 μs，并记录了全过程的数值模拟数据，颗粒的破碎形态及损伤状态分别如图4和图5所示，其中，联合损伤因子为0的单元界面为蓝色，联合损伤因子为1的单元界面为红色。结果表明，在相同的冲击持续时间下，当冲击速度小于等于50 m/s时，三维脆性颗粒均发生了碰撞反弹和局部开裂，并没有明显破碎；当冲击速度大于等于75 m/s时，随着冲击速度的增加，颗粒的破碎程度和损伤情况迅速增加，颗粒由局部开裂、破碎逐渐变为粉碎；当冲击速度达到150 m/s时，矿石分解成大量的小块。

图4 破碎形态(不同色彩表示破碎后形成不同的块体)

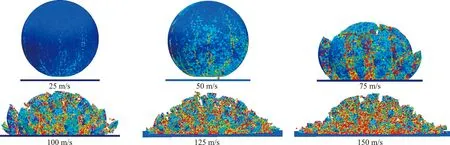
图5 损伤状态(蓝色对应损伤因子为0，红色对应损伤因子为1)

4 破碎结果与统计分析

4.1 破碎程度及损伤情况统计分析

为了表征脆性颗粒的破碎程度，分别绘制不同冲击速度下三维颗粒的特征尺寸与通过率的分级曲线以及颗粒粒径D50曲线，如图6和图7所示。当冲击速度小于等于75 m/s时，颗粒发生了碰撞反弹与开裂，并没有形成完全贯通的裂纹，破碎并不完全；当冲击速度大于等于100 m/s时，D50由 3.19 mm 变化为0.84 mm。可以看出随着冲击速度的增加，颗粒破碎越充分，且颗粒粒径D50的变化速率逐渐放缓，即随着冲击速度的增加，破碎程度的变化逐渐趋于稳定。

图6 特征尺寸与通过率的分级曲线

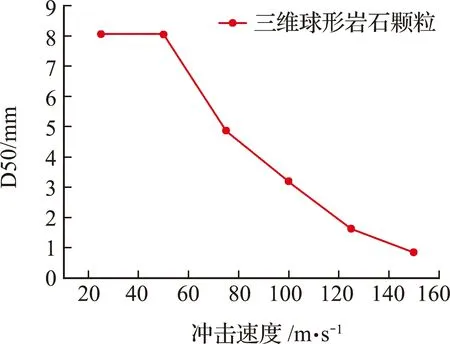
图7 冲击速度与D50级配曲线

为了表征脆性颗粒的损伤情况，分别对不同冲击速度下脆性颗粒材料的破裂度、损伤度及平均损伤因子的变化进行了统计，如图8～图11所示。

图8与图9表明，随着冲击速度的增加，颗粒材料的破裂度和损伤度在不断增加，其损伤破裂随时间演化的过程可大致分为两个阶段，第一阶段是0 μs～20 μs，在此阶段，破裂度和损伤度急剧增加；第二阶段是20 μs～150 μs，在此阶段，破裂度和损伤度的增加速率逐渐变缓并趋于平稳。

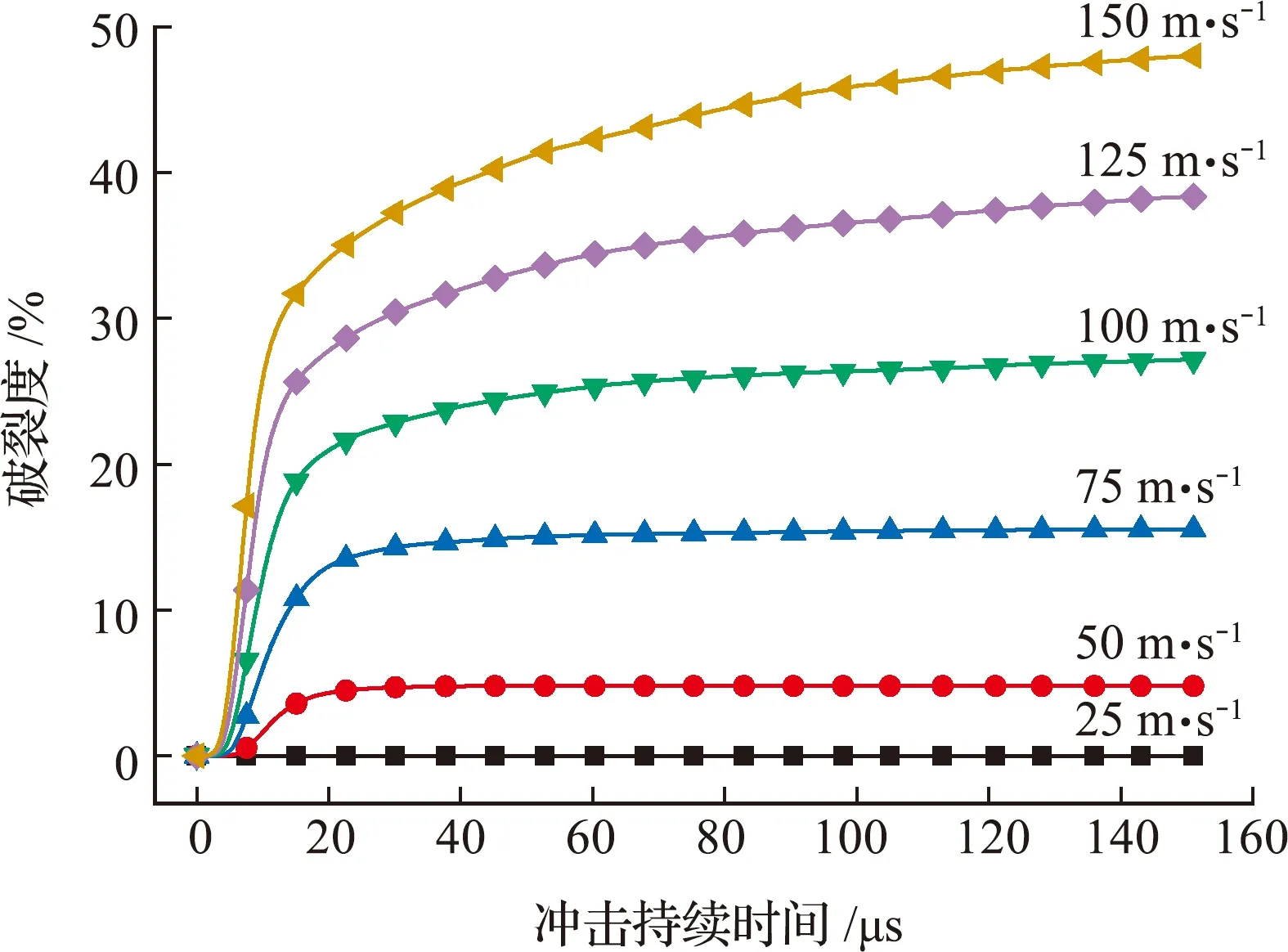
图8 冲击持续时间与破裂度曲线

图9 冲击持续时间与损伤度曲线

图10与图11表明，当冲击速度从25 m/s增加到150 m/s时，破裂度从0.01%增加到 48.04%，损伤度从3.18%增加到61.19%；平均拉伸损伤因子由0.02变化至0.59，平均剪切损伤因子由0.01变化至0.55。在冲击速度变化范围内，破裂度、损伤度以及平均损伤因子的演化趋势呈一致性变化，随着冲击速度的增加，变化速率先增加后放缓。颗粒的破裂度均大于损伤度(图10)，平均拉伸损伤因子均大于平均剪切损伤因子(图11)。

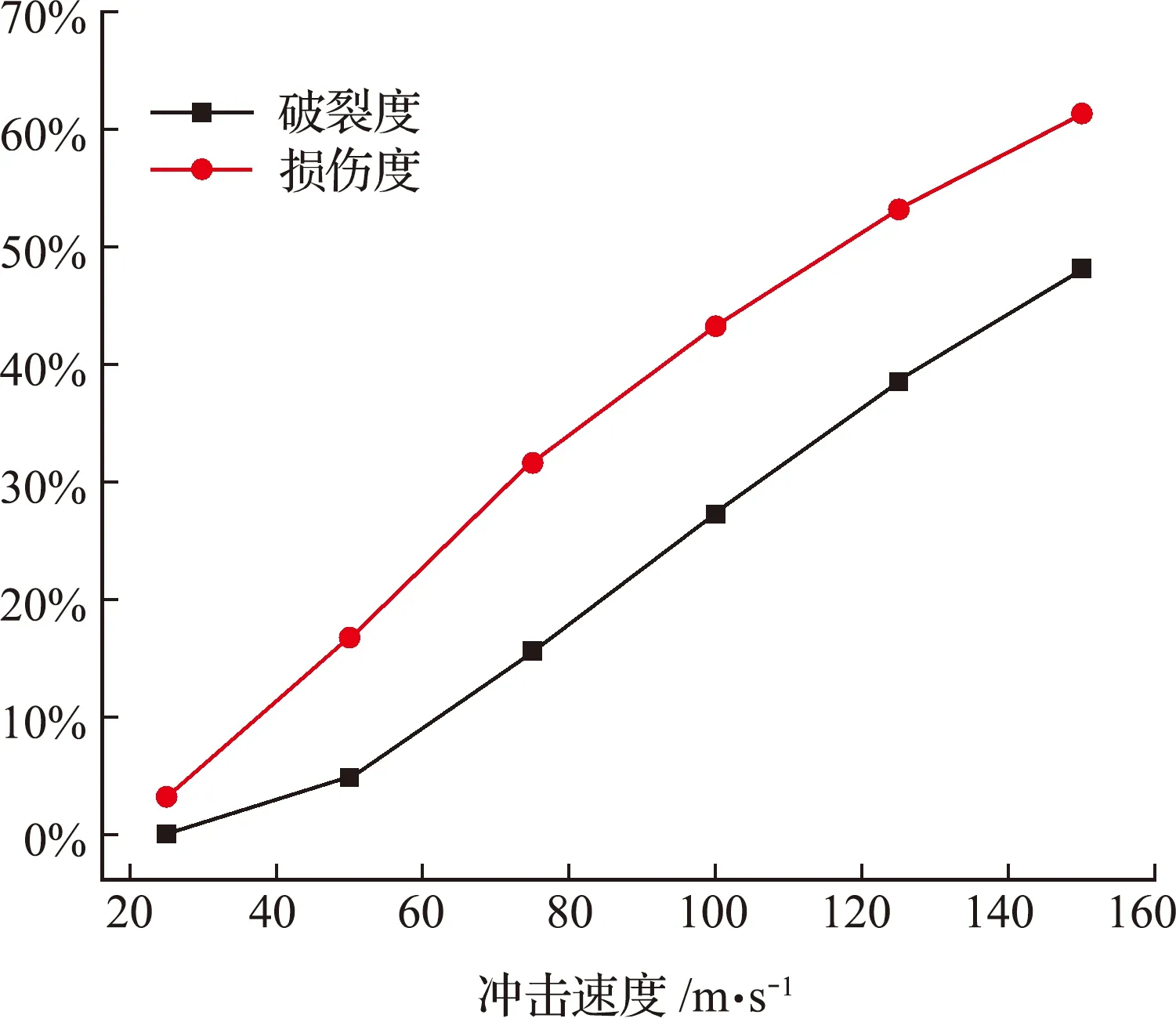
图10 不同冲击速度破裂损伤度曲线

图11 不同冲击速度平均损伤因子曲线

4.2 颗粒破碎的能量演化规律分析

为了表征脆性颗粒的能量变化特征，统计了颗粒内部的单元变形能、单元动能、弹簧变形能、弹簧断裂能、摩擦耗能和阻尼耗能，并绘制了如图12所示的不同冲击速度下颗粒能量归一化时程曲线。

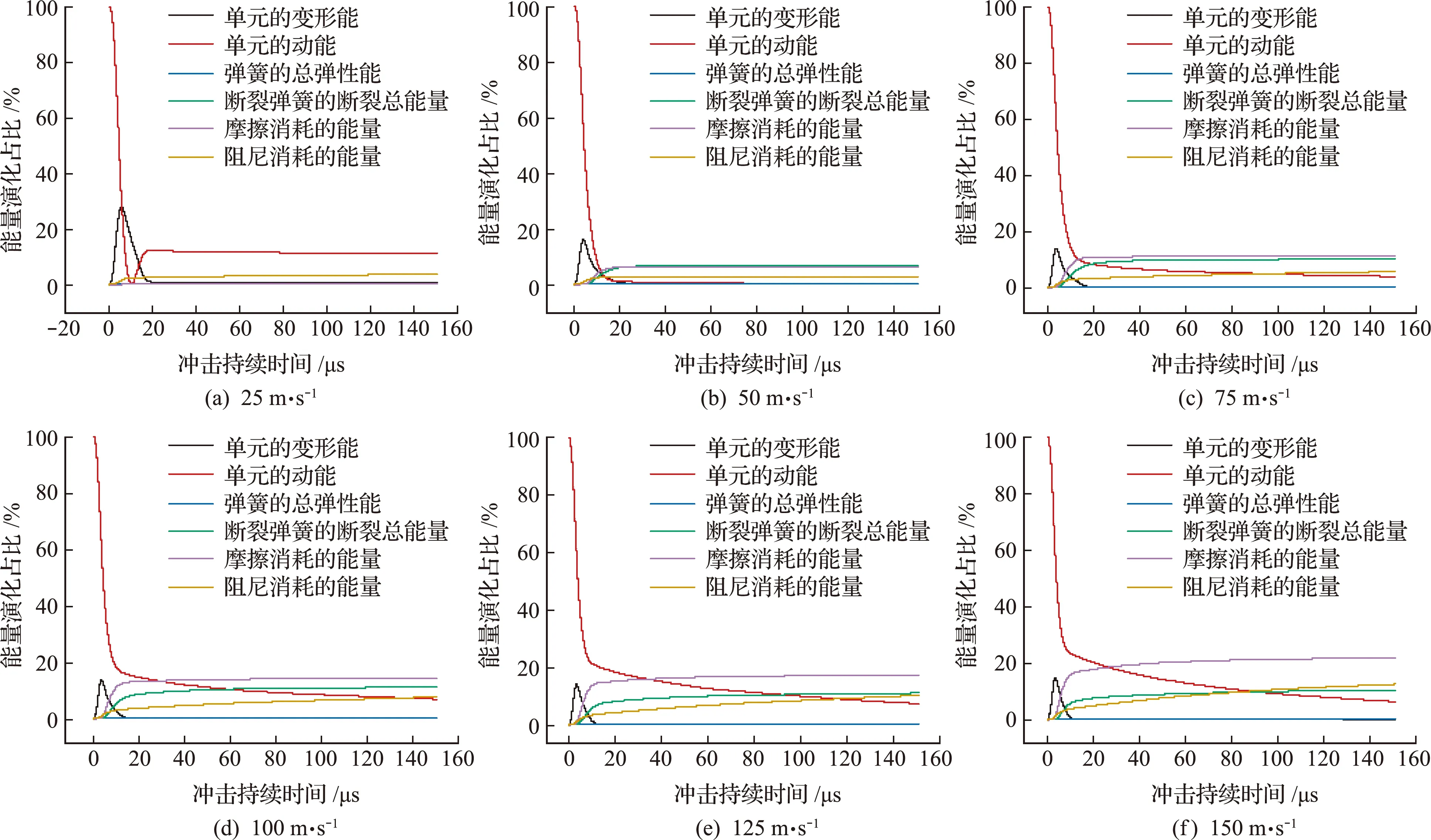
图12 不同冲击速度下颗粒能量归一化时程曲线

根据结果可以发现，整个颗粒冲击破碎过程大致分为接触蓄能阶段(0 μs～5 μs)、损伤破碎阶段(5 μs～20 μs)和碎块飞散阶段(20 μs后)三个阶段。当冲击速度为25 m/s时，颗粒动能较小，仅发生了碰撞接触，紧接着发生了反弹开裂，并没有形成完全贯通的裂纹，基本没有发生破碎，故此冲击速度下颗粒内部的能量主要为动能和单元弹性能的转化以及阻尼能量的耗散；当冲击速度大于等于50 m/s时，在碰撞接触阶段，颗粒的部分动能迅速转化为单元的变形能，随后在破碎阶段，单元变形能和单元动能主要转化为摩擦消耗、阻尼消耗以及弹簧断裂能，而弹簧的弹性变形能基本没有发生变化。随冲击速度的增加，摩擦耗能、弹簧断裂能以及阻尼耗能逐渐增加，而单元的弹性变形能基本不变。冲击过程持续到第150 μs，当冲击速度大于等于50 m/s时，颗粒内部的摩擦耗能最高，随着冲击速度的逐渐增加，阻尼耗能逐渐超过界面弹簧的断裂能，单元残余动能次之，界面弹簧弹性能和单元弹性变形能基本为0。

5 结 论

基于连续-非连续单元法(CDEM)，对不同冲击速度下球体颗粒的断裂和破碎过程进行了模拟，并对破碎过程的能量演化特征和破碎后的块度分布进行了分析，结论如下。

(1) 破碎损伤情况。不同的冲击速度下，脆性颗粒出现了反弹、开裂、破碎和粉碎等现象。随冲击速度的增加，D50的变化速率逐渐放缓，颗粒的D50由3.19 mm变化为0.84 mm，破碎块度逐渐趋于稳定。随冲击速度的增加，破裂度、损伤度以及平均损伤因子的变化速率先增加后放缓，脆性颗粒的破裂度从0.01%增加至48.04%，损伤度从3.18%增加至61.19%，平均拉伸损伤因子由0.02变化至0.59，平均剪切损伤因子由0.01变化至 0.55。颗粒的破裂度均大于损伤度，颗粒破坏以拉伸破坏为主。

(2) 能量演化情况。脆性颗粒的冲击破碎大致分为接触蓄能(0 μs～5 μs)、损伤破碎(5 μs～ 20 μs)和碎块飞散(20 μs后)三个阶段。破碎过程中，随冲击速度的增加，用于颗粒破碎的摩擦耗能、弹簧断裂能以及阻尼耗能逐渐增加，其中颗粒的摩擦耗能最高；随着冲击速度的逐渐增加，阻尼耗能逐渐超过界面弹簧的断裂能。