基于斐波那契数积分计算非等径颗粒视角系数

包 涛， 高若晗， 谭援强*

(1.华侨大学 制造工程研究院，厦门 361021；2.脆性材料产品智能制造技术国家地方联合工程研究中心，厦门 361021)

1 引 言

粉末床在化学工程、核工业、粉末冶金和激光增材制造等许多科学和工业领域中起着重要作用。粉末床在实际工况中涉及许多物理现象，包括颗粒材料的流动和压实、颗粒之间的能量传递以及颗粒的粘结和偏析机制[1-3]。粉末床传热对零件成形质量具有重要影响，引起了众多学者的关注[4-6]。热传导、热对流和热辐射都有助于热传递，尤其热辐射在高温下具有重要意义。如处于1100 ℃环境的碳化硅粉体体系内，以热辐射方式进行的热通量占据热传递总量的35%；如果将材料换为玻璃颗粒，其占比将达到85%左右[7]。在颗粒烧结和熔化时，由于是局部输入能量，粉末床中的热辐射更加重要。

粉末床中填充颗粒的多尺度使得监测变得极为困难，因此，很少有人在颗粒尺度进行热传导实验研究。通过数值模拟的方法可以更好地理解粉末床的传热机理[8,10]。目前，已经提出了基于有限元和离散元等许多颗粒间的传热模型，还针对粉末床的有效导热系数提出了几种经验公式进行预测[11,13]。然而，在大规模或动态颗粒系统中，颗粒之间的热辐射不能忽略。但现有热辐射模型在计算成本与准确性这两个方面不能同时达到数值模拟的要求。

粉末床热辐射研究常用的模拟方法可分为两类。第一类是基于连续体的方法，将粉末床视为多孔介质，使用微分方程对边界条件进行描述。有研究表明，由于热辐射强度的测量和计算仅在接近法线方向上一致，基于连续体不能很好地对含有大颗粒的非等温粉末辐射特性进行模拟[14]。第二类是基于离散的方法，将热辐射视为颗粒表面之间发生的局部效应，这样，分析粉末床中热辐射的关键就转化为计算两个颗粒之间的热辐射通量。

采用Voronoi图方法研究和分析粉末床中的热辐射，该方法考虑了包括热辐射在内的三种传热机制[15-17]。但该方法的问题是无法对颗粒之间存在障碍物时的视角系数进行计算。使用射线追踪和蒙特卡罗等随机的方法和其他技术也可以对粉末床中的辐射特性进行计算[10,18-20]，但计算结果的精度在很大程度上取决于所使用的射线数或采样点的分布，因此难以获得高精度的结果，而且要耗费很大的计算成本。

热辐射数值模拟的主要难点在于物体间视角系数的计算。卜昌盛等[21]对颗粒间的传热进行了详细的分析，并建立了一个考虑颗粒内部导热、颗粒粗糙表面传热和颗粒表面气膜与接触间气膜导热等多种因素的传热数值模型。陈宇杰[22]针对颗粒间热辐射受到阻碍这一特征，提出了考虑阻碍存在的颗粒间传热辐射的影响。该方法将阻碍物之间的复杂辐射情况进行简化，逐一计算了颗粒间的辐射热通量。Feng等[23,24]提出了一种高效和高精度的计算方法，计算由相同大小球体组成的随机粉末床中球体之间的视角系数。该方法的局限性主要在于没有考虑粉末床中的颗粒粒径的差异。大多数工业应用中涉及的颗粒粒径不是单一的，通常遵循高斯分布、双峰分布和多元分布。

本文是在Feng等[23]工作的基础上，提出一种新的数值程序，用于计算粉末床中非等径颗粒之间的视角系数。首先采用斐波那契数列对非等径颗粒表面进行离散，并且在z方向上进行非均匀变换以提高计算精度，最后对计算精度和效率进行评估，并与现有文献的结果进行比对。

2 非等径颗粒间无障碍视角系数计算

2.1 有限曲面间视角系数的计算

图1 两个有限曲面间视角系数示意图

表面A1对表面A2的视角系数F1 - 2表示为

(1)

同理，也可以依据视角系数的定义，推导出表面A2对表面A1的视角系数为

F2- 1=(A1/A2)F1- 2

(2)

2.2 无阻碍颗粒非等径颗粒间视角系数的计算

两表面间视角系数的计算公式是基于笛卡尔坐标系下的定积分函数。除一些简单的几何情况外，求解视角系数函数的解析解是极具挑战性的。

因此，本文使用了一个新的两颗粒间视角系数的计算公式，不仅减少了计算时间，还提高了计算精确度，与以往文献比较验证了该方法的可实现性和高效性。

假设一对半径分别为r1和r2的球形颗粒(r1≥r2)，两颗粒间距可表示为g≥0。两颗粒之间的视角系数可以简化为一个半径为1和一个半径为r2/r1两颗粒间的视角系数，此时颗粒间距转换为g/r1。假设p1=r2/r1,p2=g/r1，可将讨论范围转换为一对半径分别为1和p1，以及其间距为p2的一对颗粒之间的视角系数。在全局笛卡尔坐标下，颗粒S1的球心与坐标原点重合，颗粒S2的球心位于坐标点(0,0,1+p1+p2)。

为了计算颗粒S1对颗粒S2的视角系数，两颗粒分别沿z轴方向划分为三个区域，如图2所示。

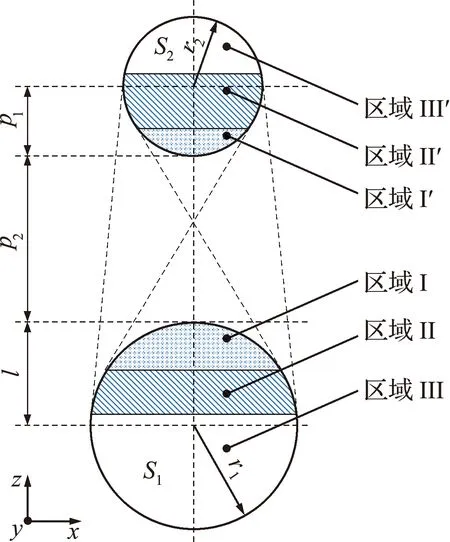
图2 两颗粒中不同区域的划分

颗粒S1对颗粒S2的视角系数可表示为[23]

F=FS - 1+FS - 2

(3)

其中

(4)

(5)

(6)

通过求解定积分可以得到两颗粒间的视角系数的精确解，并且计算结果由两个自变量决定，即

F=F(p1,p2)

(7)

2.3 非等径颗粒的斐波那契积分

使用斐波那契数列原理对颗粒表面进行离散。此方法是将颗粒放置于圆柱坐标系中，在[0,2π]×[-r,r]区域内将颗粒表面进行离散。因此，两颗粒间视角系数可以表示为

g(xi,xj)FN(p1,p2)

(8)

式中NF为斐波那契数，局部圆柱坐标系下的第NF +1个离散点的坐标和加权分别表示为

wi=4πr2/NF

(i=0,…，NF) (9)

(10)

(11)

式中

(12)

2.4 斐波那契积分的非均匀变换

在对两颗粒间视角系数计算时，除采用斐波那契数列原理对颗粒表面进行离散外，还引入非均匀变换以提高计算精度。

定义x∈[-a,a]的函数f(x)，其定积分形式为

(13)

引入新的变量x′，x′和x的关系可以定义为

x=τ(x′),x′∈[-a,a]

(14)

则式(13)可转换为

(15)

上述非均匀变换方法应用于z方向积分，则修正后的变换方程τ(z)可表示为

τ(z)=z+rsin(πz/r)/π

(16)

式中r为球形颗粒的半径，对τ(z)求导可得

τ′(z)=1+cos(πz)/r

(17)

因此，计算视角系数的张量形式可写为

(18)

2.5 斐波那契积分方案的计算与验证

斐波那契数列积分方案的计算精度取决于使用的斐波那契数列项数的取值。本算例NF,p1和p2的取值分别为NF={13,21,34,55,89,144,233,377,610},p1={0.1,0.3,0.7,1},p2={0,0.01,0.02,0.05,0.1,0.5,1,2,4,6 8}。将计算结果与式(1)计算的精确值进行比较。在一定参数p1,p2和FN条件下，斐波那契数列积分方案估算的两颗粒间的视角系数FN(p1,p2)与精确值F(p1,p2)之间的相对误差如图3所示。

图3 不同p1和p2下，斐波那契数列积分获得两颗粒间视角系数的相对误差

可以看出，当FN取为55时，已经可以获得较低的相对误差值(最大5%)。

将p1=1作为特例，把计算结果和文献进行对比。如图4所示，明显看出当FN=55时，两种方法计算结果非常吻合。

图4 斐波那契数列积分法计算获得视角系数与文献对比[22,23]

3 非等径颗粒间存在阻碍颗粒视角系数的计算

实际颗粒体系中，两颗粒间可能会存在多个阻碍颗粒。本节考虑了两颗粒间存在第三个颗粒阻碍其视角情况下视角系数的计算。将粉末床中的所有颗粒视为两目标颗粒的障碍将耗费大量的计算成本,因此有必要减少搜索区域以更有效地检测障碍物。球心位于阴影搜索区域的颗粒有可能成为两个颗粒S1和S2的视角系数的阻碍颗粒，其中rmax表示颗粒体系中最大的颗粒半径，如图5所示。

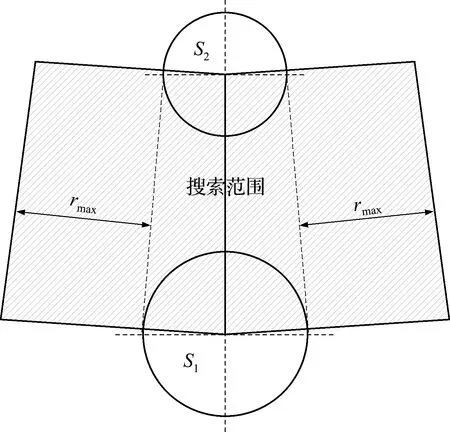
图5 两颗粒间搜索中间阻碍颗粒的搜索范围

考虑两个颗粒S1和S2间存在一个阻碍颗粒S3情况下其视角系数的估算,只需要添加判断两个样点连成的光线是否与阻碍颗粒表面相交即可。

3.1 光线阻碍检查

在图6中，假设光线从颗粒S1表面上样点x1指向颗粒S2表面上样点x2，中间阻碍颗粒的球心坐标为O3，则阻碍颗粒球心距离光线之间的距离为

图6 两颗粒间视角系数(中间存在一个阻碍颗粒)

dc=‖e×r‖/‖e‖

(19)

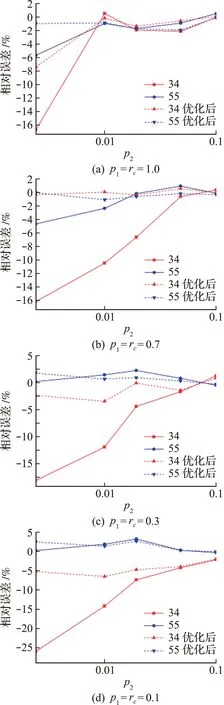
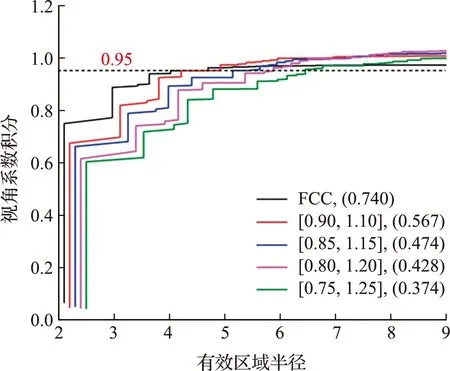
若dc

由此，提出视角阻碍函数vb，添加第三颗粒S3后，两颗粒间视角系数FN(p1,p2,Ω)表示为

v(xi,xj)[g(xi,xj)+

(20)

式中Ω为阻碍颗粒，且视角阻碍函数vb可表示为

(21)

3.2 计算和优化

为验证斐波那契数列积分法在两颗粒间存在第三颗粒情况下估算的适用性，本文计算了当NF={34,55,89,144,233,377,610,987}情况下两颗粒间的视角系数。为了对估算结果进行系统化对比，设定第三颗粒rc=p1，并假设第三颗粒始终与其他两颗粒相切接触。为方便讨论，规定F(p1,p2,Ω)表示受第三颗粒阻碍后获得的视角系数精确值，F(p1,p2)表示中间无阻碍颗粒的视角系数精确值，F(Ω)表示受第三颗粒阻碍而减少的视角系数精确值，则

F(p1,p2,Ω)=F(p1,p2)-F(Ω)

(22)

在斐波那契数列积分估算中，受第三颗粒阻碍后获得的视角系数估算值、中间无阻碍颗粒的视角系数估算值、受第三颗粒阻碍而减少的视角系数估算值分别表示为FN(p1,p2,Ω),F(p1,p2)和FN(Ω)，则

FN(p1,p2,Ω)=FN(p1,p2)-FN(Ω)

(23)

当FN值取足够大时，估算值误差极小。因此本文假设当FN=987时获得的两颗粒间存在阻碍颗粒情况下获得的估算值FN(p1,p2,Ω)即为精确值F(p1,p2,Ω)。

图7显示了当参数NF={34,55,89,144,233,377,610}、p1={1,0.7,0.3,0.1}且p2={0,0.01,0.02，0.05,0.1,0.5,1,2}情况下，斐波那契数列积分法估算的两颗粒间视角系数FN(p1,p2,Ω)与准确值FN=987(p1,p2,Ω)之间的相对误差。可以看出，相对误差是不稳定的，但是当FN=55 时，其相对误差始终小于6%。

图7 当rc=p1且p1=1，0.7，0.3，0.1情况下，斐波那契数列积分法估算两颗粒间视角系数相对误差随p2的变化

为提高颗粒间视角系数计算的精度，需要对其进行优化。假定斐波那契数列积分法估算两颗粒间视角系数在中间有无阻碍颗粒两种情况下的估算精度相同，即

(24)

则经过优化后的视角系数可表示为F′(p1,p2,Ω)，即

(25)

鉴于当NF值或p2值较小时，利用斐波那契数列积分法估算两颗粒间视角系数精度低，对第三颗粒直径rc=p1情况进行优化。求NF={34,55}，p1={1,0.7,0.3,0.1}，p2={0,0.01,0.02,0.05,0.1}情况下的视角系数的优化值F′(p1,p2,Ω)。在NF={34,55}且p2={0,0.01,0.1}情况下，经过优化后的颗粒间视角系数的最大相对误差分别由 18.11% 下降到 7.41%，5.71% 下降到 2.71%，-38.11% 下降到20.9%，12.55%下降到10.2%，如图8所示。由此可以发现，在NF较小情况下，经过优化后的视角系数估算值，即F′(r1,r2,g,Ω)可以很大程度上提高计算精度。

图8 当rc=p1时，改进后计算方法与优化前计算方法计算精度对比

将以上提出的斐波那契数列积分法优化后两颗粒间视角系数与文献的计算结果在图9中进行对比，可以看出，当NF=55且p1=rc情况下，两种方法获得的估算基本一致。

图9 优化后斐波那契数列积分法的两颗粒间视角系数与文献计算结果对比[23,24]

4 非均匀颗粒视角系数的计算与评价

斐波那契积分方案可以进行光线跟踪并且对位置分布进行优化。为了保持合理的计算效率，需要确定球体与目标球体之间的距离，以便在填充床中对其进行视角系数的计算。

为了保持合理的数值精度，令NF={34,55,89,144,233,377,610}并用于后续计算。本文将通过几个算例对非均匀颗粒间的视角系数进行计算，并对计算的准确性和效率进行评估。

4.1 精度评估

本文利用斐波那契数列积分法计算了堆积密度分别为0.74，0.567，0.474，0.428和0.374的颗粒体系。其中第一种为标准面心立方结构(FCC)、其余四种为修改后的面心立方结构，即颗粒半径r∈[rlow,rhi]的均匀分布。

选择每个部件中心的球体作为目标球体，球体的半径设置为1，计算该球体与其他球体的视角系数。每个组件产生的空间足够大，因此目标球体发出的辐射将由组件中的一些球体完全接收。显然，随着距离目标球体的总和距离的增加，所有视角系数的总和将趋向于1，这是总和的精确值，如图10所示。

图10 距离目标颗粒不同区域半径内，目标颗粒对所有颗粒视角系数的积分值

此外，接近1的速率随颗粒分布而变化。随着堆积密度的降低，视角系数总和趋向1的速率减慢。通常，有效区域半径值越大，视角系数的精度越高，但涉及的计算成本越高。可以看出，当D大约为6时，颗粒视角系数的积分可以达到95%。结果表明，在不同球数的填充床中，用该方法计算的视角系数在6D内可达到5%的相对误差。

4.2 效率评估

为了评估提出的颗粒组合方法的整体效率，考虑了六个随机堆积的组件，在0.8～1.2之间均匀分布。每个组件的颗粒数N分别为10，50，100，500和1000。为了进行适当的计算效率比较，本文将每个球体的有效域D的半径设置为6。

表1列出了两种方法计算视角系数所需的时间。将本文方法的计算时间与蒙特卡洛法的计算时间进行比较，计算效率提升了大约30%。

表1 含有N个颗粒的颗粒系统计算所有视角系数所耗费的时间

5 结 论

本文提出了一种计算非等径颗粒视角系数的数值方法。该方法的关键是三种技术的新颖组合，即两个非等径颗粒视角系数的简化积分表达式、球体上斐波那契积分方案和非均匀变换的组合。简化积分不仅提供了一个简单的积分公式，用于计算两个非等径颗粒之间的无阻碍视角系数的精确值，而且在提高计算有阻碍颗粒视角系数精度中起着基础作用。斐波那契积分方案的张量积形式本质上是一种光线跟踪方法，对于计算视角系数的对偶积分而言，是一种计算量较少但具有足够精度的方法。使用特定的非均匀变换可以很好地调节两个积分的性质，从而提高斐波那契积分法的求解精度。

对于具有阻碍颗粒的两个非等径颗粒的视角系数，从已经实现的几个算例评估了该方法的准确性。此外，还以p1=1作为特例，将本文获得的视角系数与文献的结果进行比较，显示出了较好的一致性，尤其在NF=55的情况下。对于含有多颗粒粉末床中的视角系数，多个算例的结果表明，在有效区域尺寸D=6时，计算多颗非等径颗粒视角系数的相对误差为5%，并且与传统的蒙特卡洛方法相比，计算效率提高约30%。