腹板嵌入式外包U形钢-混凝土组合梁抗剪性能研究
2022-07-04杨远龙孙天培韩劲钧
杨远龙,孙天培,韩劲钧,3
(1. 山地城镇建设与新技术教育部重点实验室,重庆 400045;2. 重庆大学土木工程学院,重庆 400045;3. 新城控股集团股份有限公司,上海 200062)
外包U形钢-混凝土组合梁是在冷弯或者焊接的U形钢内浇筑混凝土,并通过适当的抗剪连接件与上部混凝土翼缘板结合,两者共同作用的一种新型组合梁[1−3]。与传统的钢-混凝土组合梁[4−6]相比,外包U形钢-混凝土组合梁除具有更高的承载力和刚度外,还具备以下优点:1) 内部填充混凝土对U形钢腹板提供了有效的支撑,可以延缓甚至防止钢材发生局部屈曲[7];2) U形钢可作为内部混凝土和上部翼缘板浇筑的模板,从而加快施工进度;3) 在火灾下,内部混凝土可以吸收U形钢传递的热量,在U形钢失效后内部混凝土和纵筋可暂时作为钢筋混凝土梁,延缓组合梁的整体破坏。
近年来,各国学者对外包U形钢-混凝土组合梁进行了研究,提出多种形式的组合梁构造及抗剪连接件措施[8−10]。Ipe等[11]设置弯起钢筋和传统栓钉连接件对冷弯薄壁钢-混凝土组合梁进行了抗弯性能试验研究,结果表明:组合梁的承载力和延性都高于钢筋混凝土梁。Liu等[12]研究了角钢连接U形钢-混凝土组合梁的受弯性能。Turetta等[13]对外包钢-混凝土组合梁进行了足尺受弯试验,该组合梁表现出了很好的延性,内部钢筋混凝土梁和U形钢梁组合作用良好,在发生较大变形后,试件因翼缘板和下部腹板分离而破坏。林于东等[14]对12根U形钢-混凝土组合梁进行了静力试验研究,提出了抗弯承载力计算公式。石启印等[15−17]提出了一种新型焊接外包钢-混凝土组合梁,其研究证明了这种组合梁良好的承载力和延性,但在施工过程中焊接工作量较大。沈建华[18]进行了8根薄壁U形钢-混凝土组合梁的抗剪性能试验研究,试验表明:组合梁在发生剪切破坏时仍具有良好的延性,组合梁整体抗剪承载力中需要考虑翼缘板的影响。张婷[19]进行了两种不同抗剪连接形式的外包U形钢组合梁的静力性能试验研究,结果表明:钢与混凝土交界面除发生纵向滑移外,还存在竖向掀起,并根据试验结果提出了抗弯、抗剪、界面抗剪承载力计算公式。Zhou等[20]、Liu等[21 − 22]和Zhao等[23−25]提出了一种新型外包U形钢-混凝土组合梁,钢-混凝土界面抗剪采用钢筋桁架、倒U形插筋等构造,使开口的U形钢截面转化为等效闭口箱型截面,并进行了抗弯、抗剪、抗扭等一系列试验研究。研究表明:这种新型组合梁具有良好的力学性能,内部钢筋桁架和倒U形插筋的存在使混凝土翼缘板和U形钢腹板的组合作用良好。
目前,国内外研究的外包U形钢-混凝土组合梁仍将栓钉、角钢等作为主要抗剪连接件[26],这类连接件在安装过程中需要耗费较大焊接工作量,一定程度上增加了施工工期,且产生了焊接残余变形。嵌入式连接件则是通过激光在钢板上切割出各种形状的钢榫,通过钢榫和混凝土榫的咬合传递界面纵向剪力,使钢与混凝土两者协同工作,既减轻了焊接工作量,又能节省利用率不高的上翼缘。嵌入式连接件在PBL连接件[27]、PZ连接件[28 − 29]上发展而来,李国强等[30−32]在PZ连接件的基础上提出了燕尾形抗剪连接件,设计出腹板嵌入式倒T形钢-混凝土组合梁,对其进行了抗弯、抗剪性能试验,并提出了相应承载力计算公式。
由以上研究可知,当前关于外包U形钢-混凝土组合梁的研究多数集中于对其抗弯性能的研究,其抗剪性能的研究相对较少。国内外设计标准尚未有针对这种组合梁抗剪承载力的设计方法,而采用传统钢-混凝土组合梁的抗剪设计方法对外包U形钢-混凝土组合梁进行设计将明显低估其抗剪承载力,造成材料利用上的浪费。同时,当前关于嵌入式连接件的研究方法主要集中于推出试验研究和有限元分析,针对腹板嵌入式组合梁的试验研究相对较少。关于嵌入式连接件在组合梁中,尤其在外包U形钢-混凝土组合梁中的具体性能表现尚待进一步研究。
本文研究了腹板嵌入式外包U形钢-混凝土组合梁(Web-embedded U-shaped Steel-concrete Composite Beam,简称WUSCB)的抗剪性能。构造如图1所示。翼缘板和腹板界面采用与钢腹板一体的嵌入式抗剪连接件,且U形钢内部浇筑混凝土与翼缘板混凝土连成整体。考虑梁剪跨比、混凝土翼板宽度、连接件间距及倾角、底部纵筋直径、栓钉和箍筋设置、U形钢腹板高厚比等参数的影响,对WUSCB试件进行试验研究和有限元分析,分析总结了WUSCB试件的剪切破坏模式和抗剪力学性能。进一步提出WUSCB的抗剪承载力计算方法,为外包U形钢-混凝土组合梁的工程设计和应用提供了新的思路和建议。
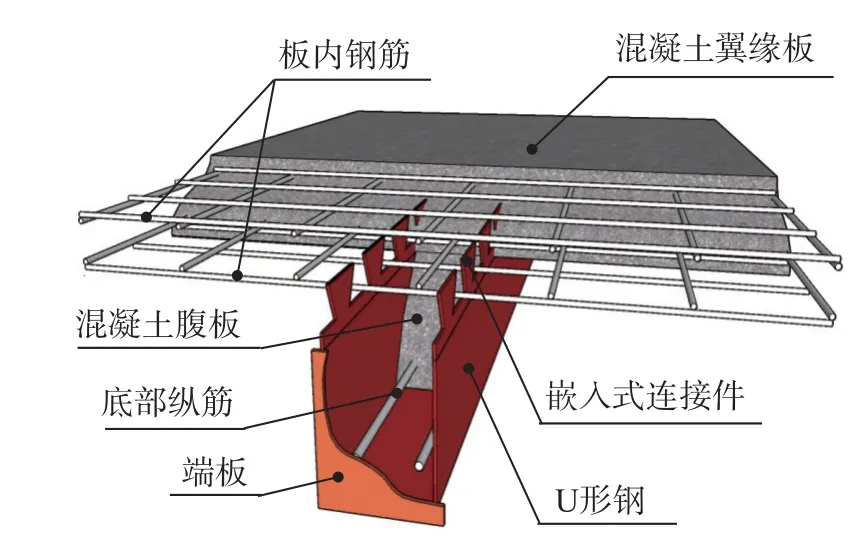
图1 WUSCB试件构造图Fig. 1 Structural configuration of WUSCB
1 试验设计
1.1 试件设计
设计了9根设置燕尾形嵌入式连接件的简支组梁试件,试件的基本参数如下:梁长度L=1500 mm,有效跨径(支座间距) L0=1200 mm,梁总高度H=300 mm,外包U形钢高度hs=180 mm,U形钢底板宽度bs=150 mm,混凝土翼缘板厚度D=120 mm。试验考察的参数包括U形钢壁厚(ts)、连接件间距(ds)、混凝土翼缘板宽度(B)、底部纵筋直径(φd)、剪跨比(λ)、底部栓钉、箍筋设置(φh)和连接件倾角(θ) (见表1)。标准试件CB-1和其他试件的截面如图2所示,其中底部栓钉间距、箍筋间距与嵌入式连接件的间距保持一致,均为150 mm。混凝土翼缘板内钢筋依照文献[33]中构造要求进行配筋。
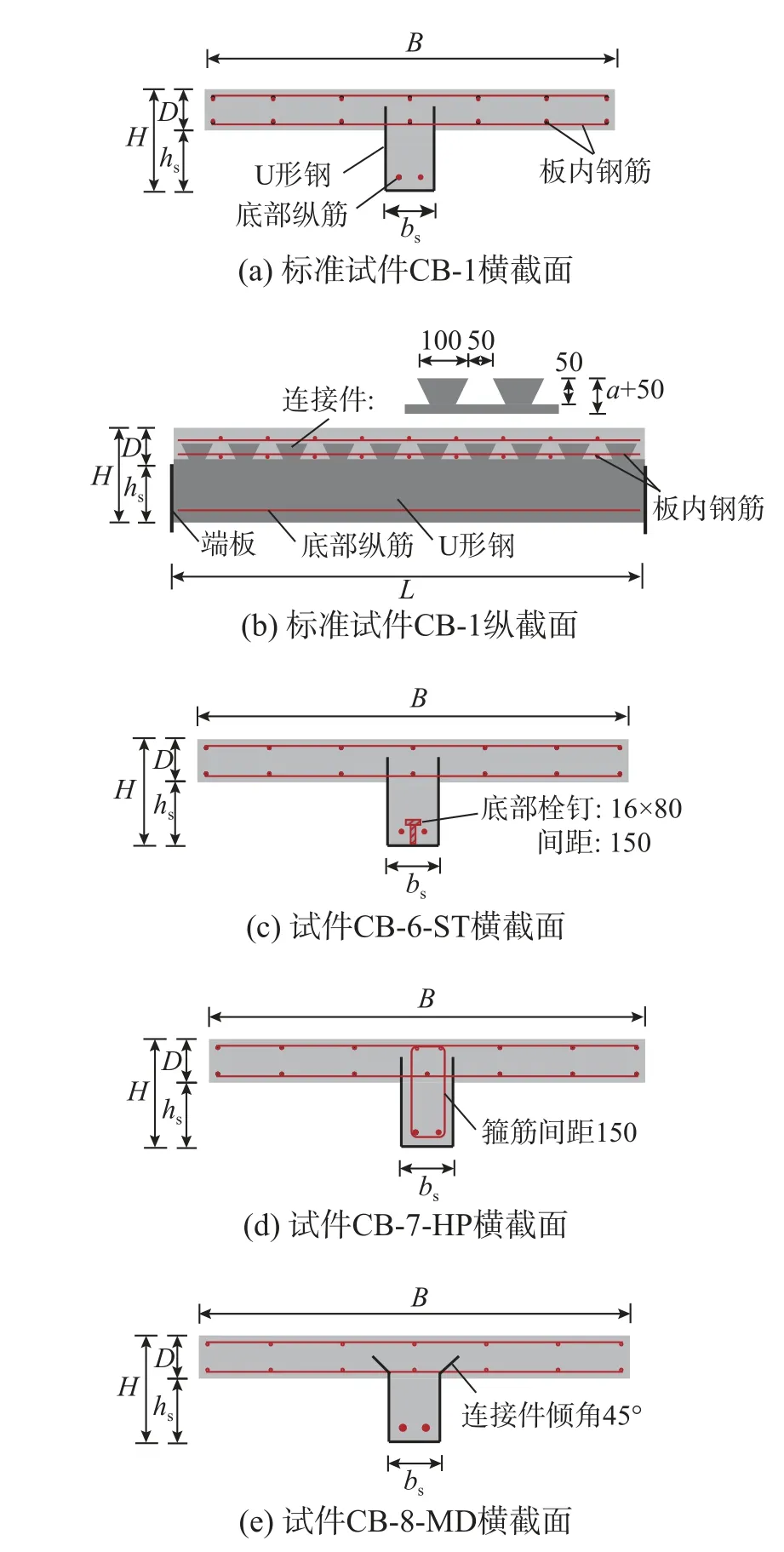
图2 WUSCB试件截面图 /mmFig. 2 Cross section of WUSCB specimens
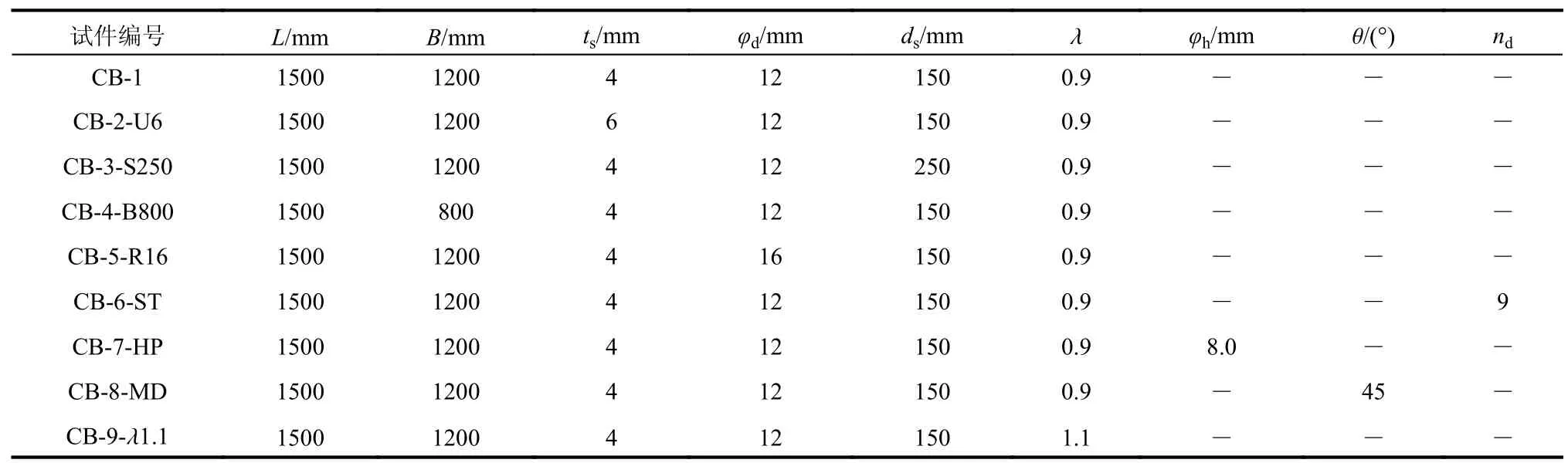
表1 WUSCB试件参数表Table 1 Design details of WUSCB specimens
1.2 试件材性试验
试件翼缘板混凝土和腹板混凝土的强度等级设计为C40,浇筑时同时制作边长为150 mm的混凝土立方体试块,并与试件在相同环境下养护。试验前测得混凝土立方体抗压强度fcu,k=42.3 MPa,根据我国《混凝土结构设计规范》(GB 50010−2010)[33],换算得到轴心抗压强度fc,k=28.3 MPa,混凝土弹性模量Ec=3 3109 MPa。按照文献[34]测得试件钢材力学性能参数如表2所示。
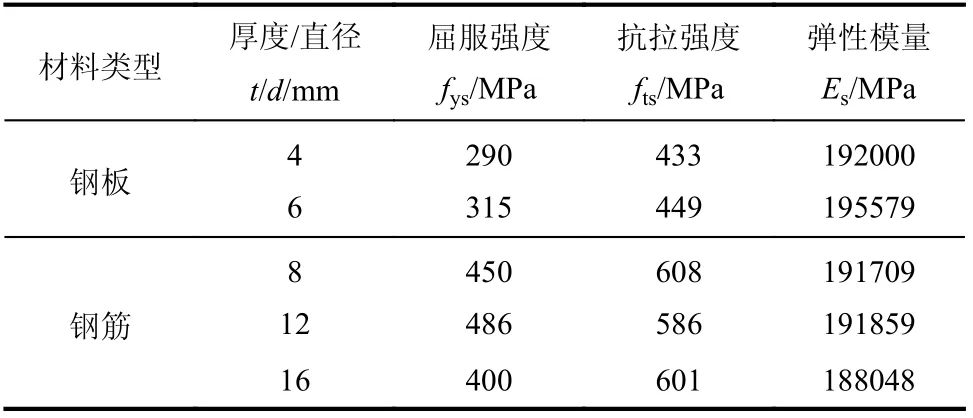
表2 钢材材料属性Table 2 Measured material properties of steel
1.3 加载与测量方案
① 加载方案
试验在重庆大学土木工程学院振动台实验室进行,加载方案如图3所示,试件两端底部分别设置滑动铰支座和固定铰支座,达到简支的边界条件。加载时采用200 t液压千斤顶进行加载,通过一根刚度较大的分配梁将荷载分为两点施加到组合梁试件上。在千斤顶与分配梁之间布置一个量程为2000 kN的压力传感器,以传输和记录实时荷载。
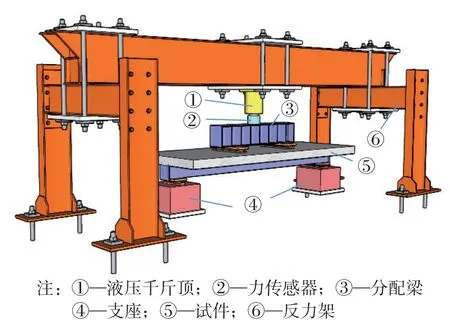
图3 加载方案示意图Fig. 3 Loading diagram
② 加载制度
在试验正式开始前进行预加载,以确保各仪器设备处于工作状态,同时消除各装置之间贴合不紧密的问题,预加载荷载为试件预估极限承载力的20%。正式加载过程采用荷载-位移混合控制方法。在弹性阶段,采用力控制加载,每级加载50 kN;当试件荷载-位移曲线刚度折减时,改为位移控制加载,每级加载2 mm,直至达到试件峰值荷载;在荷载下降段,进行慢速率连续加载;当荷载下降到峰值荷载的85%时,认为试件失去承载能力,试验结束。
③ 测量方案
试件的测量方案如图4所示。
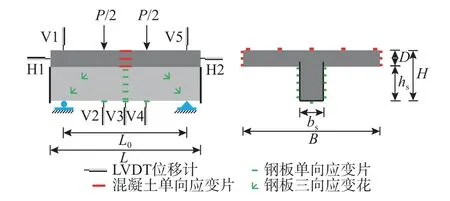
图4 测量方案Fig. 4 Measurement scheme
在试件跨中截面和加载点截面底部布置3个位移计(LVDT),测量试件的挠度变化(V2、V3、V4);在支座处混凝土翼缘板顶部布置2个位移计(LVDT),测量加载过程中的支座沉降量(V1、V5);在试件端部设置2个位移计(LVDT),测量翼缘板和腹板之间的相对滑移(H1、H2)。为观测试件跨中截面的正应变分布、U形钢底板的纵向应变变化以及剪跨段U形钢腹板的应力变化,对试件布置了应变片和应变花。
2 试验结果及其分析
2.1 试验现象与破坏模式
2.1.1 试件试验现象
各试件的试验现象和破坏模式均类似,下面以试件CB-1和试件CB-2-U6为例进行描述。
试件CB-1为本试验的标准试件。加载初期,试件处于弹性阶段,组合梁的跨中挠度随荷载的增加呈线性增长。加载至250 kN(0.22Pu,Pu为峰值荷载),支座处混凝土翼缘板顶出现第一条纵向裂缝,并逐渐向加载点延伸,如图5(a);加载至350 kN(0.31Pu)时,加载截面混凝土翼缘板底出现沿板宽方向延伸的横向裂缝,并迅速发展至板侧,如图5(b)。随着加载的进行,混凝土板底横向裂缝由加载截面向跨中发展,并布满整个纯弯段,板顶逐渐形成两条通长的纵向裂缝,如图5(c)和图5(d)所示。加载至800 kN(0.71Pu),U形钢底板达到屈服,试件刚度开始折减,此时跨中挠度为1.97 mm(L0/609);达到峰值荷载1120.30 kN(Pu)时,剪跨段翼缘板顶纵向裂缝向板边分叉发展,裂缝区域不断拓宽,并伴有小块混凝土掀起现象,如图5(d)所示,此时跨中挠度为6.55 mm(L0/200)。在荷载下降阶段,跨中挠度快速增长,位于剪跨段的U形钢腹板发生局部屈曲,且由于内部混凝土的支撑,屈曲为向外的一个屈曲半波,混凝土板侧出现斜裂缝并快速发展,贯穿整个板厚,如图5(e)。当荷载下降至峰值荷载的85%时,试验结束,此时跨中挠度为20.11 mm(L0/60)。试验结束后,切开U形钢观察到,腹板混凝土在剪跨段形成了由加载点到支座位置的平行斜裂缝和斜混凝土短柱,后者已被压溃,如图5(f)所示。根据以上现象,试件CB-1的破坏模式为斜压破坏。


图5 试件CB-1试验现象Fig. 5 Test phenomena of specimen CB-1
试件CB-2-U6在达到峰值荷载前的试验现象与标准试件CB-1基本类似,如图6(a)和图6(b)。达到峰值荷载后,在荷载下降阶段,试件跨中挠度快速增长,剪跨段翼缘板顶裂缝区域不断拓宽,板顶裂缝发展至板端部,并在端部形成倒八字形裂缝,如图6(c)。同时混凝土翼缘板侧出现斜裂缝并快速发展,贯穿整个板厚,如图6(d)。当荷载下降至峰值荷载的85%时,试验结束。该试件腹板U形钢未发生局部屈曲。剥开U形钢后发现,剪跨段腹板混凝土形成斜混凝土柱并压溃,如图6(e)所示。基于以上现象,试件CB-2-U6的破坏模式为斜压破坏。

图6 试件CB-2-U6试验现象Fig. 6 Test phenomena of specimen CB-2-U6
其他试件的破坏模式与标准试件CB-1相似,整体上均发生斜压破坏。钢腹板出现局部屈曲,混凝土翼缘板出现斜截面剪切破坏和端部冲切破坏,腹板内部混凝土则在加载点和支座连线上出现平行斜裂缝和斜向混凝土短柱压溃的现象。
2.1.2 典型破坏模式总结
总体而言,WUSCB试件在0.9和1.1剪跨比下的破坏模式均为斜压破坏。试件典型破坏过程(图7)可分为以下三个阶段:
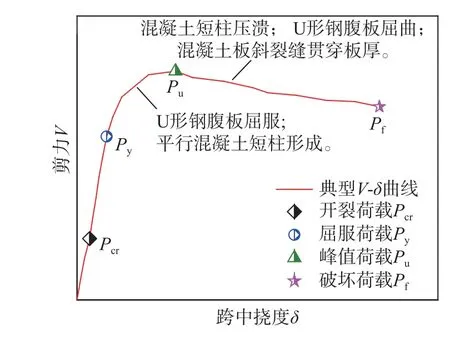
图7 试件典型破坏过程Fig. 7 Typical failure process of specimens
① 线弹性阶段(0段~Py段):U形钢板和内部混凝土组合作用良好,共同承受由加载点向支座传递路径上的剪力。在该阶段,混凝土板顶出现由抗剪连接件导致的纵向裂缝;混凝土板底出现横向的受弯裂缝,但在小剪跨比下,这些裂缝对整体刚度的影响很小。因此,跨中挠度随荷载的增大呈线性增长。
② 弹塑性阶段(Py段~Pu段):U形钢底板屈服后,曲线进入弹塑性阶段,刚度开始减小。剪跨段U形钢腹板逐渐屈服。当钢腹板全截面屈服后,其对组合梁整体抗剪承载力的贡献不再增加,内部混凝土承担了更多的剪力。由此可推断出,内部混凝土的斜裂缝在该阶段内产生。一旦平行的混凝土短柱形成,剪跨段的内部混凝土即达到抗压强度,荷载达到峰值。
③ 荷载下降阶段(Pu段~Pf段):当平行混凝土短柱压溃时,曲线进入下降段。在失去内部混凝土支撑后,钢腹板发生沿主压应力方向的局部屈曲。抗剪连接件继续发挥作用,曲线进入平台段。当混凝土板斜裂缝贯穿整个板厚及端部形成冲切裂缝时,试件最终破坏。
2.2 剪力-跨中挠度曲线
图8给出了9个试件的剪力V-跨中挠度δ关系曲线,表3给出了各个试件的力学性能指标,包括初始刚度(k)、屈服剪力(Vy)、峰值剪力(Vu)、延性系数(µ)和塑性发展系数(γs)。其中,初始刚度k取为剪力-跨中挠度曲线屈服点前的割线刚度;延性系数µ和塑性发展系数γs按下式进行计算:式中:δf为当荷载下降至0.85 Pu时的跨中挠度;δy为钢梁下翼缘屈服时的跨中挠度;Vy为钢梁下翼缘屈服时的剪力;Vu为试件峰值剪力(抗剪承载力)。

整体来看,WUSCB试件具备较高的抗剪承载力和较好的延性,延性系数µ=9.56~27.22。即使发生了斜压破坏,但试件的塑性发展系数γs为1.22~1.67,表明WUSCB试件在屈服后仍有较大的承载力储备。
由图8和表3分析不同参数对组合梁剪力-跨中挠度曲线和力学性能指标的影响。
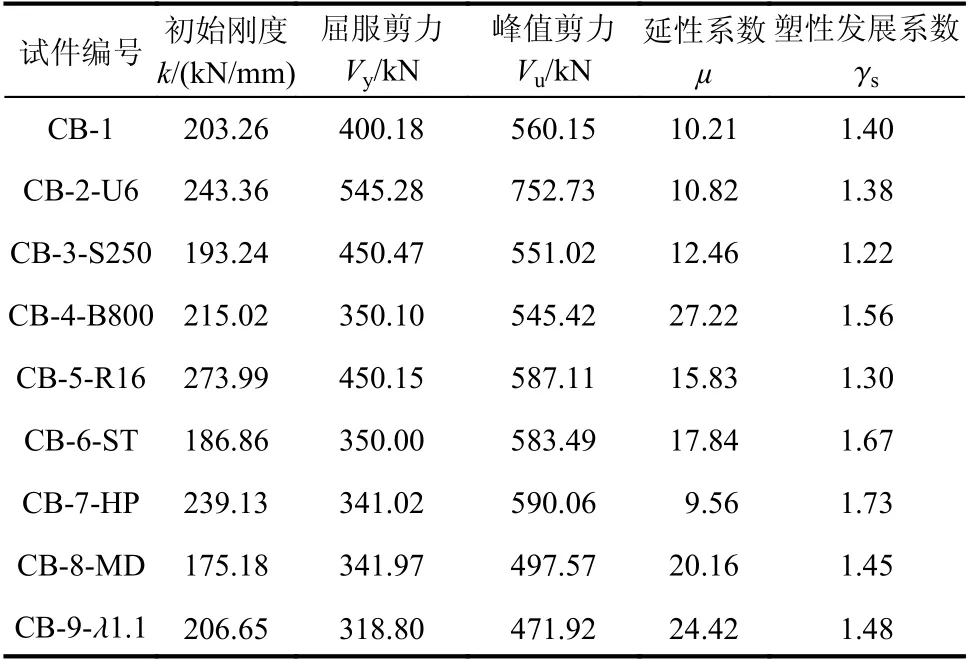
表3 试件抗剪性能指标Table 3 Shear performance indices of the specimens
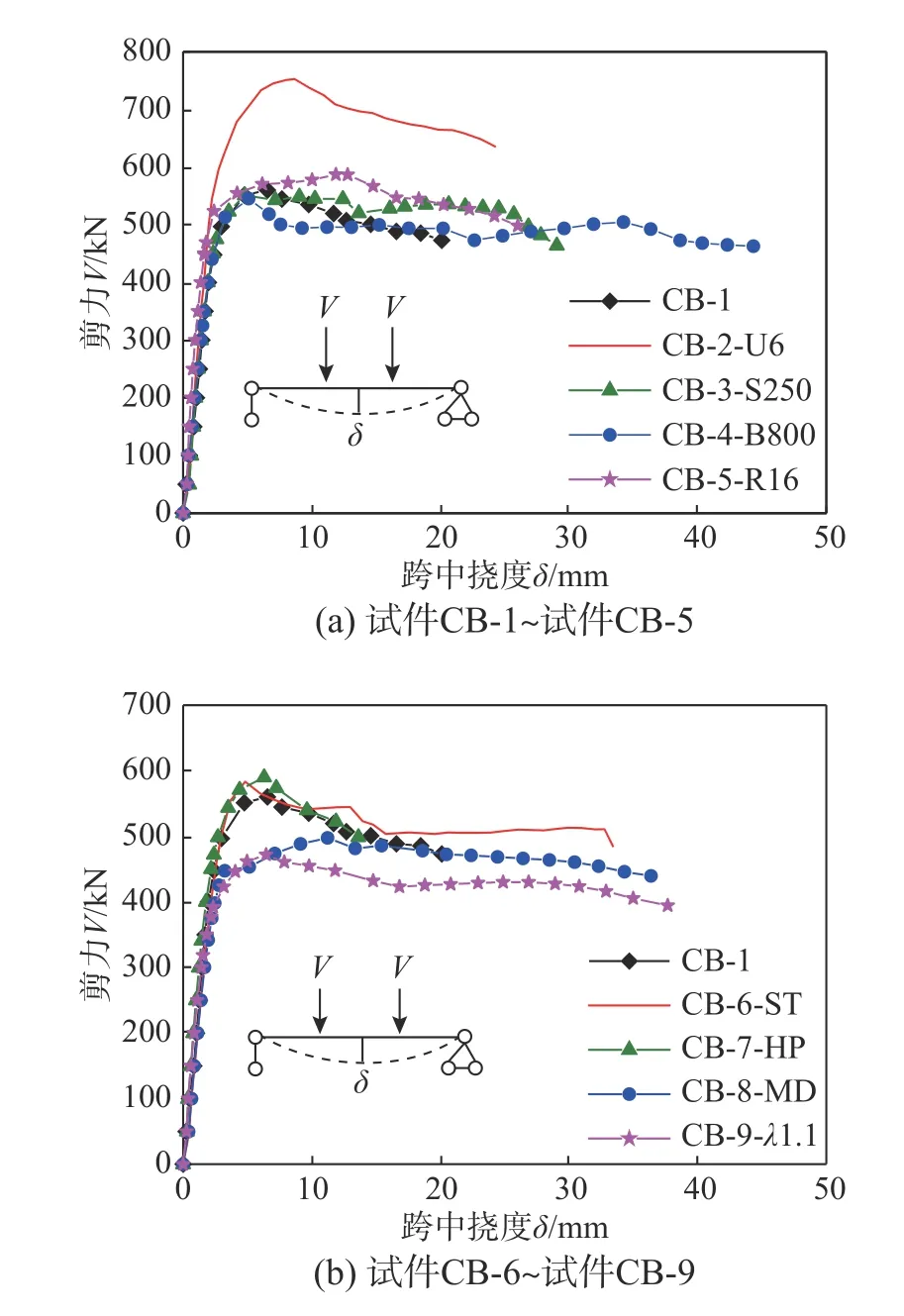
图8 WUSCB剪力-跨中挠度曲线Fig. 8 Shear force versus mid-span deflection curves of WUSCB
由试件CB-2-U6和标准试件CB-1的对比可看出,U形钢板壁厚的增加使试件的刚度增大了20%,承载力提高了34%;在延性方面则影响不大,两者仅相差6%。刚度和承载力的提高是因为钢板壁厚的增加直接增大了U形钢的受剪截面面积。
由试件CB-3-S250和标准试件CB-1的对比可看出,连接件间距由150 mm增大到250 mm对组合梁的承载力影响不大(相差1.6%),但能使延性系数提高22%,说明在满足完全抗剪连接的前提下,适当增大连接件间距使抗剪连接刚度降低,能提高组合梁延性。
由试件CB-4-B800和标准试件CB-1的对比可发现,混凝土板宽度的减小并没有使试件承载力发生显著下降,反而使延性系数提高了166%。这说明在0.9的剪跨比下,试件实际参与受剪的混凝土翼板有效宽度小于1200 mm,当混凝土板宽度过大时,可能使翼缘板边缘部分无法与中部协调变形,试件延性下降。
由试件CB-5-R16、CB-6-ST和标准试件CB-1的对比可发现,增大底部纵筋直径和增设底部栓钉对组合梁的承载力影响不大(仅分别提高5%和4%),但使延性系数分别提高了55%和75%。这说明底部纵筋和栓钉的设置有利于腹板内部混凝土和U形钢的组合作用,提高组合梁整体的变形能力。需要注意的是,CB-6-ST的割线刚度相比于CB-1降低了8%,表明栓钉可能导致附近的混凝土发生劈裂破坏,在一定程度上改变了剪力的传递路径。
由试件CB-7-HP和标准试件CB-1的对比发现,增设箍筋能在一定程度上提高组合梁的刚度(18%),但对组合梁抗剪承载力的提升并未达到预期(仅提高5%),这一结果表明:在小剪跨比下,箍筋的抗剪贡献不大,反而使组合梁的延性系数减小6%。
由试件CB-8-MD和标准试件CB-1的对比发现,试件CB-8-MD相比标准试件CB-1的割线刚度下降14%,承载力下降11%,但延性提高97%。试验现象表明:该试件端部的倒八字形裂缝在试件屈服时形成,据此推断外翻45°连接件:一方面,使连接件平面内刚度降低,释放了混凝土翼缘板和腹板之间的部分界面滑移,最终组合梁变形能力有所提高;另一方面,外翻连接件加剧了混凝土翼缘板端部倒八字形裂缝的形成,即加剧端部冲切破坏的发生,导致组合梁承载力下降。
试件CB-9-λ1.1与标准试件CB-1的对比反映了剪跨比对组合梁受剪性能的影响。当剪跨比由0.9变为1.1时,试件CB-9-λ1.1腹板内部混凝土在纯弯段的受拉裂缝增多,最终仍表现为斜压破坏。组合梁刚度变化不大,承载力下降16%,延性提高139%。因此在进行抗剪承载力计算时需要考虑组合梁剪跨比的影响。
2.3 剪力-相对滑移曲线
图9给出了各试件端部翼缘板和腹板的相对滑移变化曲线。以标准试件CB-1为例,试件翼缘板和腹板在加载前期共同协调变形,相对滑移量基本可以忽略。当剪力达到200 kN(0.36Vu)时,相对滑移量为0.03 mm,并在此后开始缓慢增长,但其变化量依旧很小,即使在峰值剪力Vu时,试件CB-1的相对滑移也仅有0.33 mm。总体而言,所有试件在峰值剪力时的相对滑移均未超过1.3 mm,试件组合作用较强。因此在研究经过合理设计的WUSCB试件的抗剪性能时,可忽略翼缘板和腹板之间相对滑移的影响。

图9 WUSCB剪力-相对滑移曲线Fig. 9 Shear force versus relative slip curves of WUSCB
2.4 荷载-应变关系曲线
2.4.1 沿板宽方向纵向应变分布
试验在各试件跨中截面的混凝土翼缘板顶沿、板宽等间距布置了5个应变片(见图4测量方案)。由于各试件在该处的应变分布规律性类似,图10给出部分试件沿混凝土翼缘板宽度方向的纵向应变分布。可观察到,荷载达到0.4 Pu前,板宽范围内的纵向应变均匀分布,相差不大。当荷载超过0.4 Pu后,板中心的应变比板边缘应变发展更快。在峰值荷载Pu时,板中心应变混凝土峰值压应力对应的应变εc,r(1628 µε)附近,比板边缘应变大38%~480%,表现出明显的剪力滞后效应,但所有测点应变均未超过混凝土的极限压应变εc,u(3793 µε)。
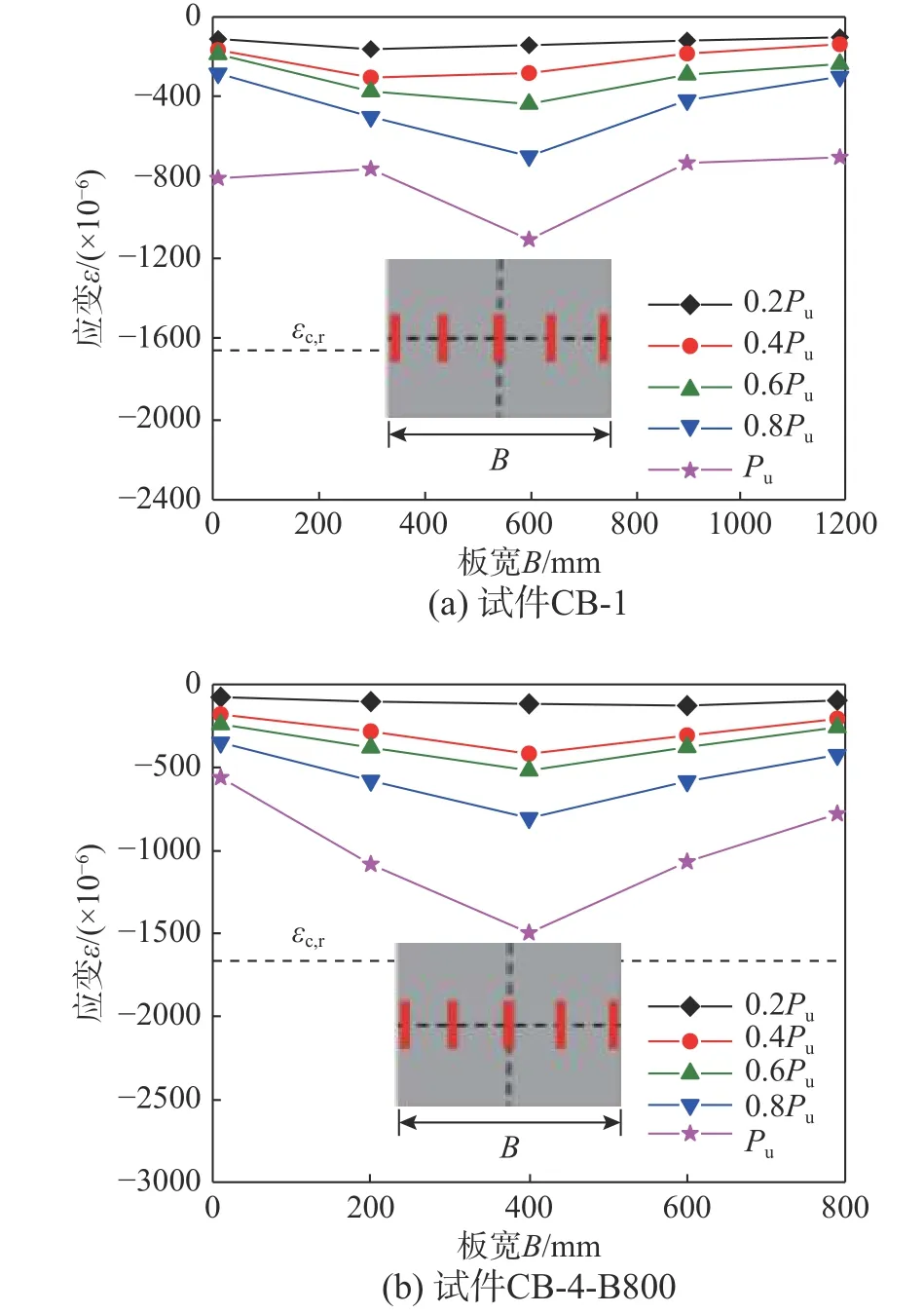
图10 沿板宽方向混凝土纵向应变分布Fig. 10 Longitudinal strain distribution along the slab width
2.4.2 跨中截面沿高度应变分布
图11给出了部分试件的跨中截面沿高度方向的纵向应变分布曲线。观察发现,在荷载达到0.6 Pu前,混凝土翼缘板和腹板组合作用良好,虽然混凝土翼缘板下部应变大于U型钢上部应变,整体截面纵向应变未呈线性分布,但截面只存在唯一中性轴且位于混凝土翼板内。随着加载的进行,由于混凝土翼缘板受拉区开裂,中性轴开始向上移动。当荷载达到0.8 Pu时,观察到U形钢腹板最下方50 mm高度范围内钢板达到屈服,混凝土板与U形钢仍表现出良好的组合效应,截面中性轴未发生分离。该现象表明,采用嵌入式的燕尾形连接件能很好地满足混凝土翼缘板和腹板之间的组合作用。在峰值荷载Pu下,混凝土翼缘板受拉区开裂严重,U形钢腹板3/4高度范围内的钢板基本屈服,试件的各测点纵向应变差距较大。
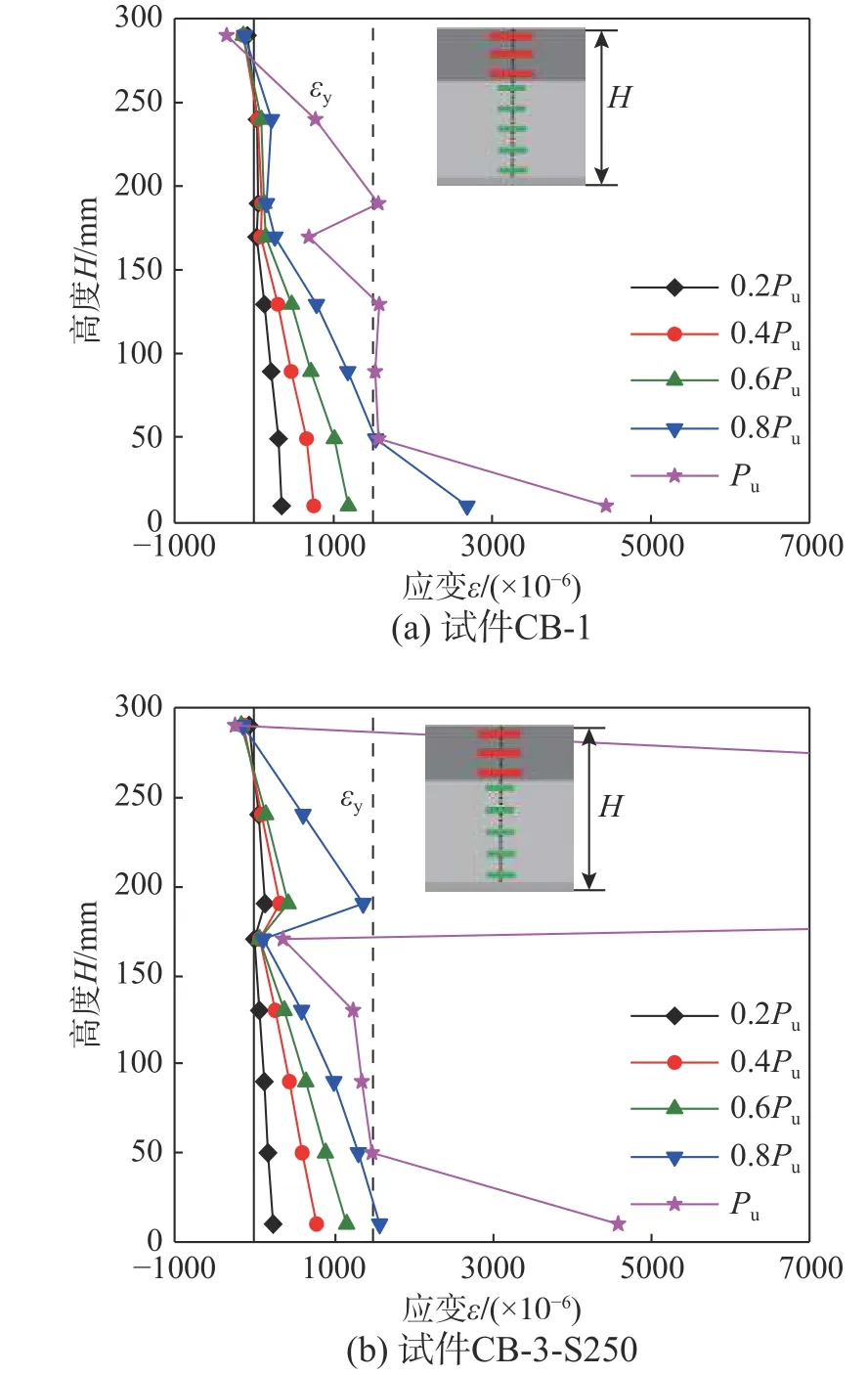
图11 跨中截面沿高度纵向应变分布Fig. 11 Longitudinal strain distributions along the height
2.5 U形钢腹板应力分析
为了确定剪跨段U形钢腹板在加载过程中的应力-应变情况,在钢腹板剪跨段位置,沿加载点和支座连线上布置了4组应变花(图4)。
当腹板处于弹性工作状态时,各测点位置的主应变(ε1、ε2)、主应力(σ1、σ2)和主应力方向α0分别由式(3)~式(5)确定:
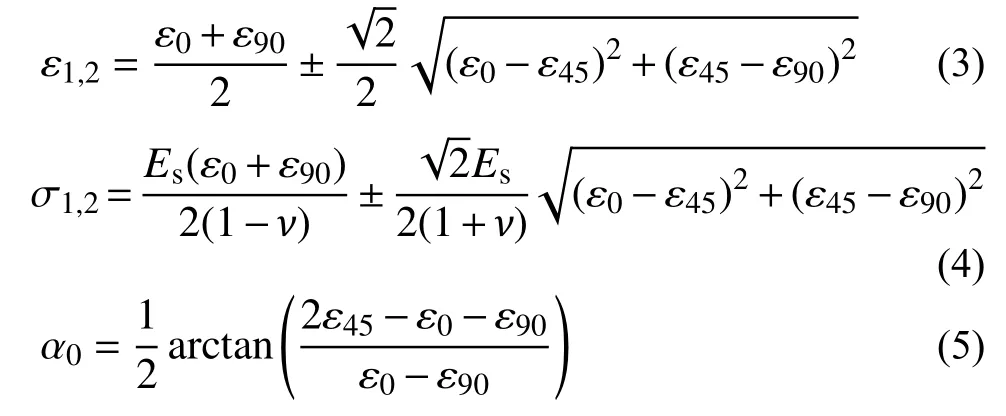
式中:ε45为应变花中倾角为45°应变片的应变值,ε0和ε90同理;ν 为U形钢截面的泊松比,取0.3。
根据Von Mises屈服准则,假定U形钢腹板处于平面应变状态,其在厚度方向上的变形可以忽略,则钢腹板的屈服判别由式(6)确定:

式中:σ0为等效应力;fys为U形钢腹板屈服强度,由材性试验确定。
当由主应力σ1和σ2确定的等效应力σ0达到钢材屈服强度fys时,该测点位置的钢板屈服,进入塑性状态。
由于各试件U形钢腹板的Mises应力变化规律相似,以部分试件为例给出钢腹板Mises应力曲线,如图12所示。可观察到,达到峰值剪力前,剪跨段U形钢腹板等效应力均已达到屈服强度。表4给出了所有试件的屈服剪力(Vy)、各个应变花测点发生屈服时的剪力值(V0y)和峰值剪力(Vu)。由表4中数据可看到,剪跨段U形钢腹板屈服剪力值V0y介于试件屈服剪力Vy和峰值剪力Vu之间,即剪跨段U形钢腹板在试件弹塑性阶段开始屈服,并在达到峰值剪力时充分屈服。
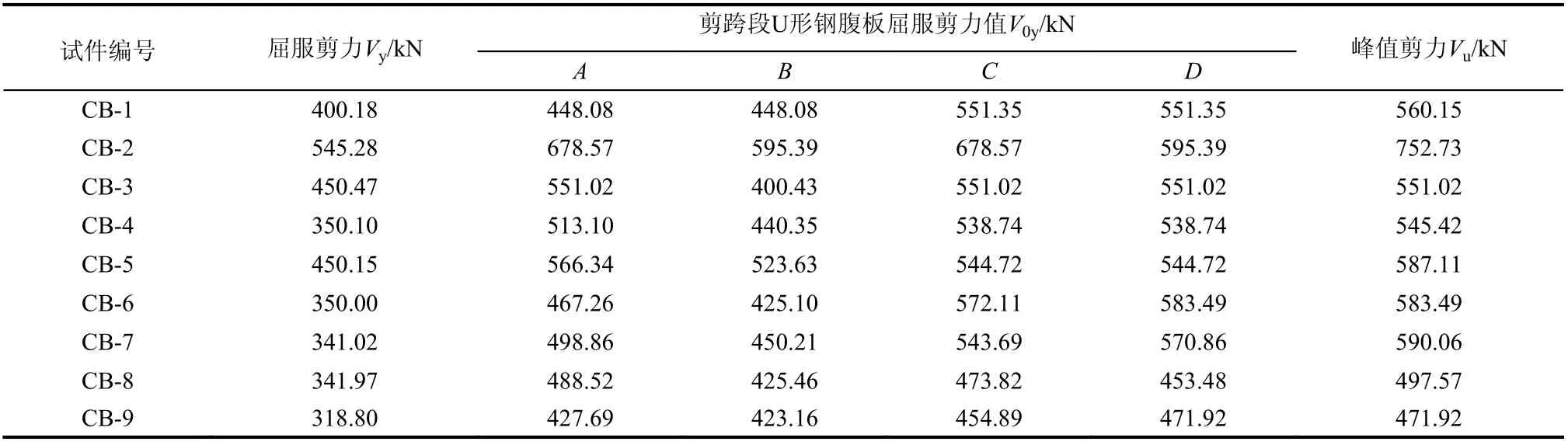
表4 剪跨段U形钢腹板屈服剪力Table 4 Yield shear force of U-shaped steel web in shear span
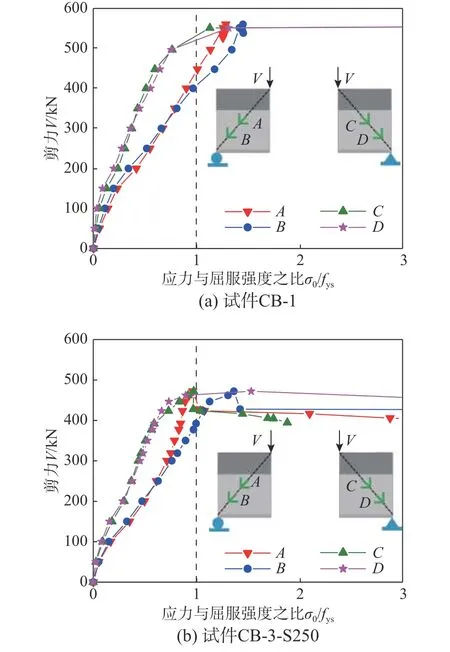
图12 Mises应力曲线Fig. 12 Mises stress curves
3 有限元分析
3.1 材料本构关系
混凝土采用塑性损伤本构模型(Concretedamage plasticity model),该本构模型中的混凝土塑性参数分别取为:ψ=15°、c=0.1、fb0/fc0=1.16、Kc=0.667、u=0.001[29]。混凝土的弹性模量和轴心抗压强度等参数见本文的材性试验。混凝土单轴应力-应变关系按《混凝土结构设计规范》(GB 50010−2010)[33]中给出的附录C进行计算。
钢材的单向应力-应变曲线采用理想弹塑性模型,弹性模量Es和屈服强度fys依据本文的材性试验结果取值(表2),泊松比取为0.3。
3.2 模型建立
3.2.1 单元类型和网格尺寸选取
本文沿对称轴取1/2模型进行建模。有限元模型中,混凝土采用八节点减缩积分的三维实体单元(C3D8R);翼缘板内钢筋和底部纵筋在加载时忽略其抗弯刚度,采用三维线性桁架单元(T3D2);由于嵌入式连接件需要通过燕尾形钢榫和混凝土榫的咬合传递界面纵向剪力,U形钢和连接件无法采用常规的壳单元(S4R),为更真实地模拟嵌入式连接件的工作机理,参考文献[29, 35]采用三维实体单元(C3D8R)建立U形钢和连接件。
混凝土网格尺寸经验证选用20 mm~40 mm,钢筋和U形钢板网格尺寸均选用20 mm,对连接件(钢榫和混凝土榫)进行局部细化,网格尺寸取为15 mm。由于本模型中U形钢部件为实体单元,沿钢板厚度方向的初始网格为单层网格,在弯矩作用下单层网格的实体单元将会出现沙漏模式,导致该部件表现过于柔软,计算结果失真,研究发现:对实体单元精细化网格后可消除沙漏模式的影响。经验证后发现单元尺寸为1 mm(四层网格)和2 mm(两层网格)两者模拟结果差异较小,且均与试验结果吻合较好。为提升计算效率,最终对U形钢在厚度方向划分尺寸为2 mm的网格。模型整体网格划分如图13所示。
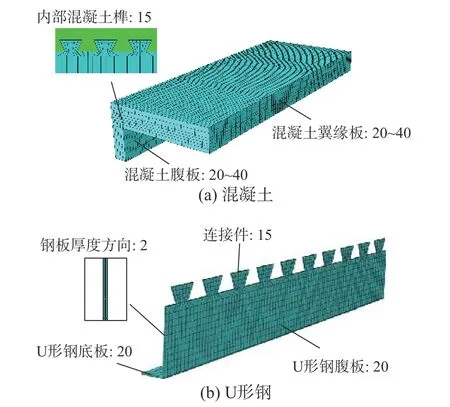
图13 网格划分 /mmFig. 13 Mesh generation of finite element model
3.2.2 相互作用和边界条件
模型中混凝土部件通过切割(Cut)功能在混凝土内部连接件嵌入位置建立了可与连接件相接触的混凝土面,因此连接件和翼板混凝土、U形钢腹板和腹板混凝土均采用面与面接触(surface-tosurface contact),接触面法向采用硬接触属性,允许两者接触后发生分离;切向采用摩擦接触,摩擦系数取为0.25[36]。翼缘板内钢筋和底部纵筋嵌固(embedded)于混凝土实体单元。为方便施加荷载,模型中建立了两块刚度较大的加载垫块,将垫块下表面与混凝土翼缘板上表面进行绑定约束(Tie)。模型的边界条件、加载方式与试验一致。
3.3 有限元模型验证
3.3.1 剪力-跨中挠度曲线对比
图14给出了部分试件有限元计算的剪力-跨中挠度(V-δ)曲线和试验结果的对比。
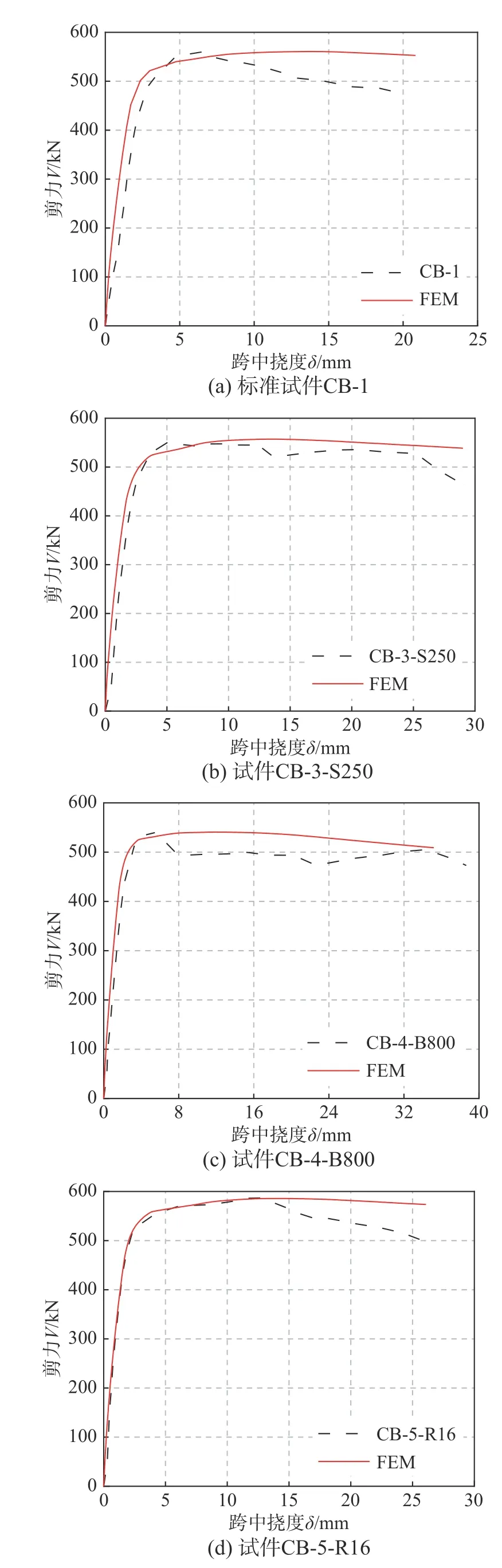
图14 剪力-跨中挠度曲线对比Fig. 14 Comparison of shear force versus mid-span deflection curves
整体来看,有限元计算的前期刚度和峰值剪力与试验结果吻合良好,但在荷载下降段,由于有限元模型对剪切破坏模式的模拟不够准确,使得有限元计算的延性略高于试验结果。
3.3.2 破坏模式对比
图15为极限状态下试件整体变形和关键部位现象与有限元模型的对比。由于各试件的主要现象相似,在此仅给出标准试件CB-1的对比图。
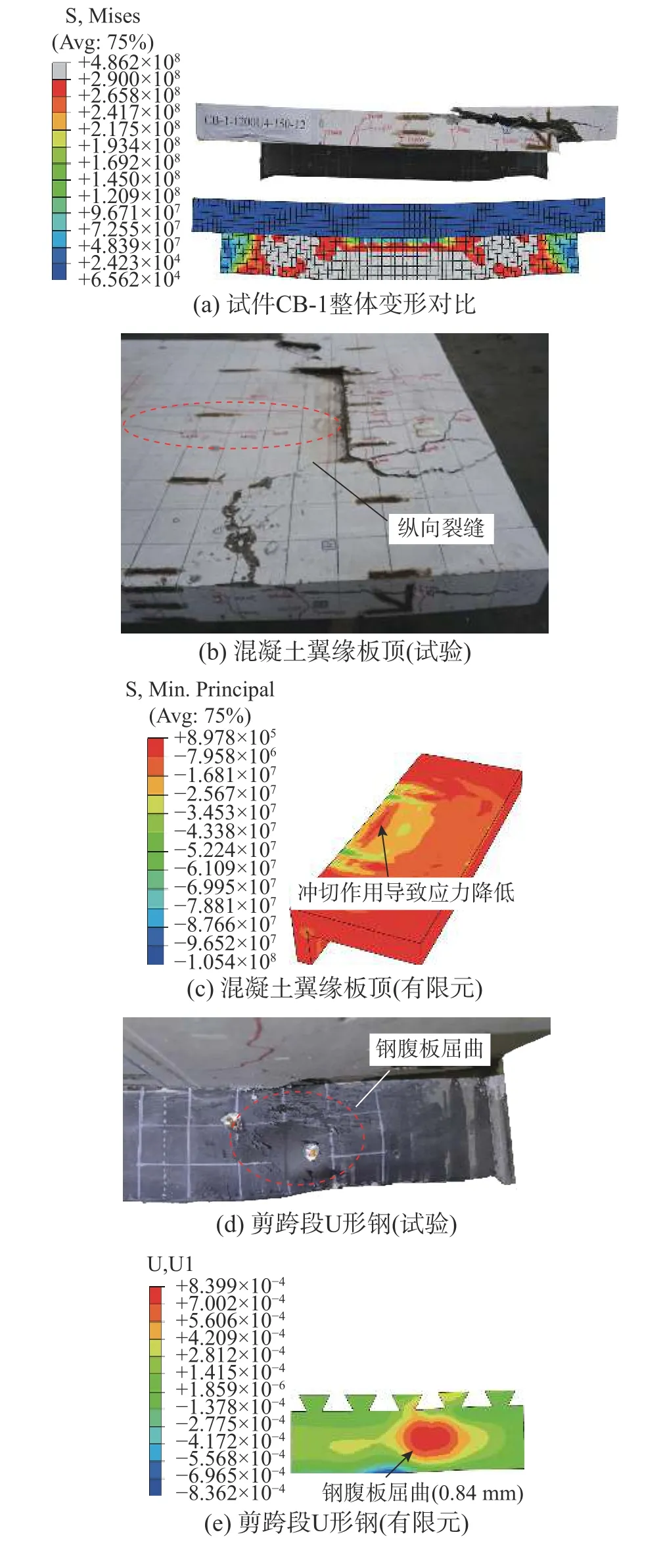
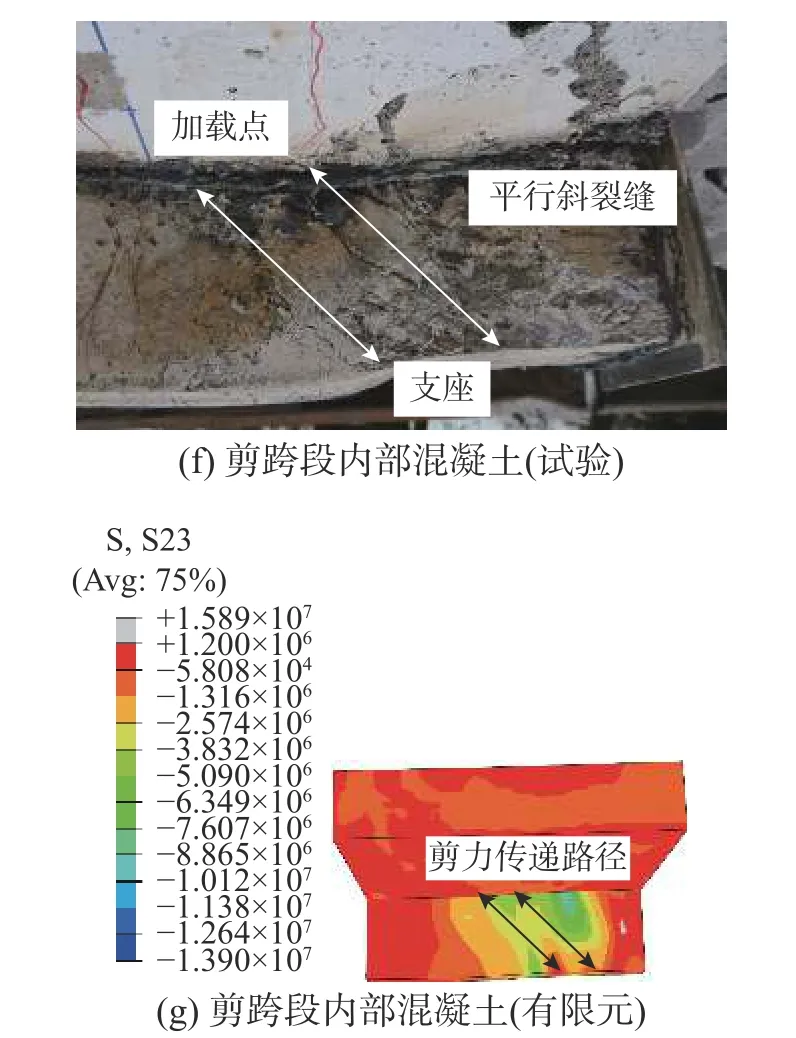
图15 标准试件CB-1破坏模式对比Fig. 15 Comparison of CB-1 failure mode
由图15(a)可见,有限元模型的最终整体挠度变形与试件相近。根据Mises应力分布图可知,模型中剪跨段U形钢腹板均达到屈服(图中灰色表示屈服),而纯弯段U形钢腹板仅2/3高度达到屈服。
由图15(b)和图15(c)可见,混凝土翼缘板顶产生的纵向裂缝在有限元中也有所体现,由于混凝土受到下方连接件的冲切作用,模型中对应位置的应力相比附近应力有所降低;由图15(d)和图15(e)可见,剪跨段U形钢腹板在试验和有限元中都发生了屈曲现象;由图15(f)和图15(g)可见,试验中腹板混凝土在剪跨段出现了沿剪力传递路径的平行斜裂缝,与有限元模型中剪跨段内部混凝土的剪应力分布相对应。
综上所述,有限元模拟得到的破坏形态和试验结果吻合良好,所建立的有限元模型能够准确模拟腹板嵌入式外包U形钢-混凝土组合梁试件的受剪性能。
3.4 组合梁参数分析
将试件CB-4-B800的设计参数作为基准试件模型默认参数,研究各参数对组合梁抗剪性能的影响。分析参数主要包括:混凝土翼缘板宽度(B)、剪跨比(λ)、腹板高厚比(η)、底部纵筋配筋率(ρd)。具体参数变化如表5所示。

表5 模型参数Table 5 Model parameter
有限元参数分析的结果见图16。分析发现,随着混凝土翼缘板宽度B的增加,组合梁抗剪承载力整体呈上升趋势,说明混凝土翼缘板的抗剪作用对组合梁整体抗剪的贡献较为显著。当B超过1200 mm后,承载力基本不再增加,表明当混凝土翼缘板宽度过大时,混凝土翼缘板并非全截面参与受剪,存在有效抗剪宽度。
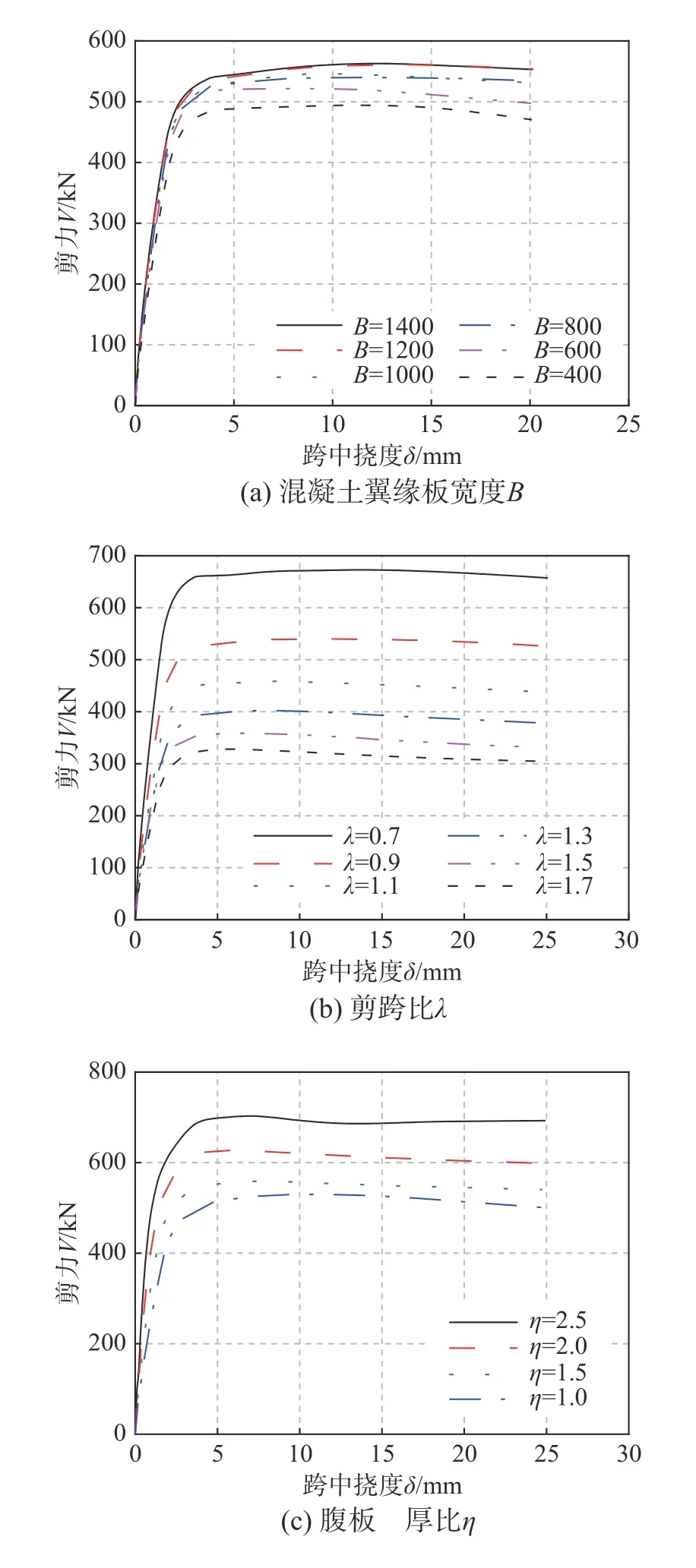
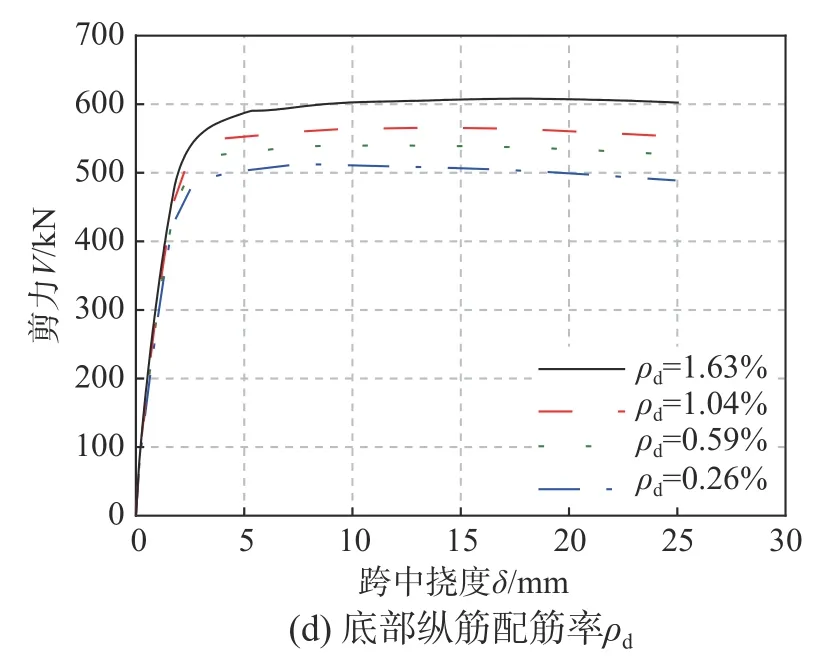
图16 有限元参数分析结果Fig. 16 The parametric analysis of FEMs
剪跨比λ的增大会使试件的前期刚度和抗剪承载力下降,剪跨比为0.7的组合梁抗剪承载力相比剪跨比为1.7的组合梁提高105.1%,由此可见,剪跨比对组合梁抗剪性能的影响较为显著。
腹板高厚比η和底部纵筋配筋率ρd的提高都会加强试件的抗剪承载力,但当η>2时,U形钢腹板整体屈曲现象较为严重,其剪力-跨中挠度曲线因此提前进入下降段;组合梁的抗剪承载力随着底部纵筋率的增加而单调上升,即使在小于1.5%的范围内,纵筋率对抗剪承载力的提升依然十分明显。因此,在计算WUSCB抗剪承载力时,需要考虑底部纵筋的影响。
4 抗剪承载力设计方法
目前,各国现有规范在计算组合梁抗剪承载力时,总体而言均假定组合梁全部剪力由钢梁腹板承担,不考虑混凝土部分对承载力的贡献,仅将其视为安全储备。国外关于组合梁的试验研究表明:混凝土翼缘板能提供总抗剪能力的20%左右[37],因此,在抗剪承载力中需考虑混凝土翼缘板甚至混凝土腹板的贡献。
文献[23]研究发现,外包U形钢-混凝土组合梁的抗剪承载力不仅需要考虑混凝土和U形钢的抗剪贡献,还要考虑腹板底部纵筋的销栓作用,由销栓作用贡献的抗剪能力占组合梁整体抗剪承载力的17%~22%。本文有限元部分的参数分析结果也表明:底部受拉纵筋配筋率对WUSCB的抗剪承载力影响显著,因此本文在计算WUSCB抗剪承载力时,同时考虑U形钢腹板、混凝土翼板和腹板、底部纵筋销栓作用三部分的抗剪贡献,如图17。
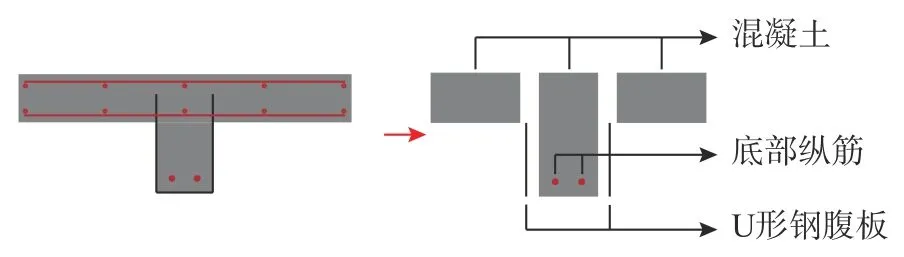
图17 WUSCB抗剪承载力组成Fig. 17 Contributions to shear capacity of WUSCB
在计算WUSCB的抗剪承载力时,做出如下基本假定:
① U形钢腹板在峰值承载力时达到屈服强度,且不考虑钢材强化;
② 在达到峰值承载力前,U形钢腹板不发生局部屈曲,腹板抗剪作用发挥充分;
③ 混凝土腹板能有效参与抗剪,达到抗剪强度;
③ 在翼缘板有效抗剪宽度内,全板厚方向的混凝土均达到抗剪强度;
④ 组合梁底部纵筋和内部混凝土不发生相对滑移。
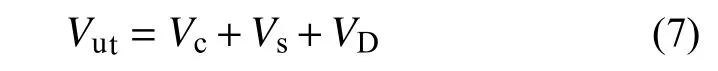
抗剪承载力按式(7)进行计算:式中:Vut为WUSCB的抗剪承载力;Vc为混凝土翼板和腹板的抗剪承载力;Vs为U形钢腹板的抗剪承载力;VD为纵筋销栓作用产生的抗剪承载力。
U形钢腹板的抗剪承载力根据文献[38]采用式(8)进行计算。
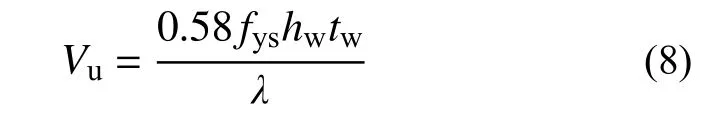
式中:Vu为U形钢的抗剪承载力;hw为U形钢腹板高度;tw为U形钢腹板厚度;fys为U形钢腹板屈服强度。
组合梁底部纵筋销栓作用产生的抗剪承载力参考文献[23]的计算方法进行计算,即:
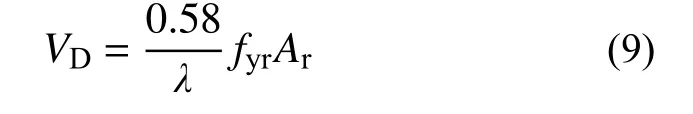
式中:fyr为纵筋屈服强度;Ar为纵筋截面积。
WUSCB中的混凝土部分可视为混凝土T形梁构件,文献[33]中关于T形截面混凝土梁在集中荷载作用下的斜截面承载力按式(10)进行计算:
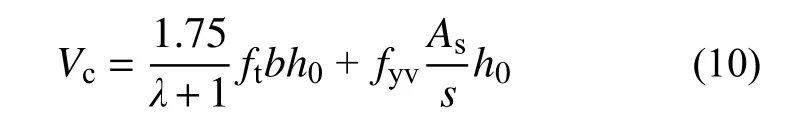
式中:λ为剪跨比,当λ<1.5时,取为1.5,当λ>3时,取为3;ft为混凝土轴心抗拉强度;b为T形梁混凝土腹板宽度;h0为截面有效高度;fyv为箍筋抗拉强度;Asv为同一截面内箍筋的总截面面积;s为箍筋间距。
有限元参数分析结果表明:随混凝土翼缘板宽度的增加,WUSCB抗剪承载力呈上升趋势,但当翼缘板宽度超过1200 mm后,承载力提高很小,表明翼缘板并非全截面参与受剪,存在有效抗剪宽度,如图18所示。
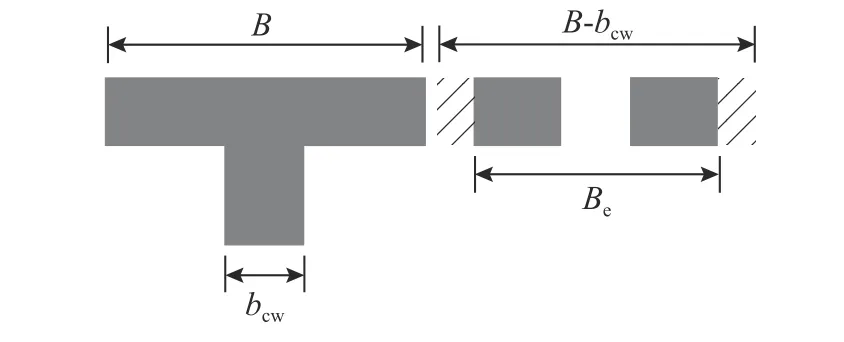
图18 翼缘板有效抗剪宽度Fig. 18 Effective shear width of overhanging concrete slab
翼缘板有效抗剪宽度与扣除腹板宽度后的翼缘板宽度的比值定义为有效抗剪宽度系数α,见式(11)。
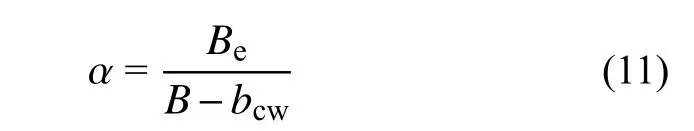
式中:Be为外伸翼缘板有效抗剪宽度;B为翼缘板宽度;bcw为混凝土腹板宽度,bcw=bs−2ts。
以翼缘板宽度B和混凝土腹板宽度bcw为变量,根据式(8)~式(10)分别计算得到U形钢腹板抗剪承载力Vs、纵筋销栓作用产生的抗剪承载力VD和混凝土腹板抗剪承载力Vcw,反算得到混凝土翼缘板的抗剪承载力Vcf。对于Vcf,假定整个厚度的翼缘板均参与抗剪,将式(10)进行修正得到有效外伸翼缘板(宽度为Be−bcw)的抗剪承载力计算式(12),由此得到外伸翼缘板有效抗剪宽度Be,如表6所示。
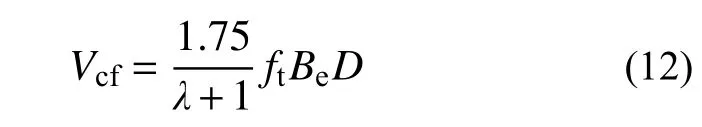
式中,D为混凝土翼缘板厚度。
根据表6的数据,选取无量纲参数m与α分别作为横、纵坐标,其中m为外伸翼缘板宽度与腹板宽度的比值,即m=(B−bcw)/bcw。通过回归分析,得到外伸翼缘板有效抗剪宽度系数α的回归曲线,如图19所示,该回归曲线与有限元计算的数据点相关度较高。因此,α按回归式(13)进行计算。
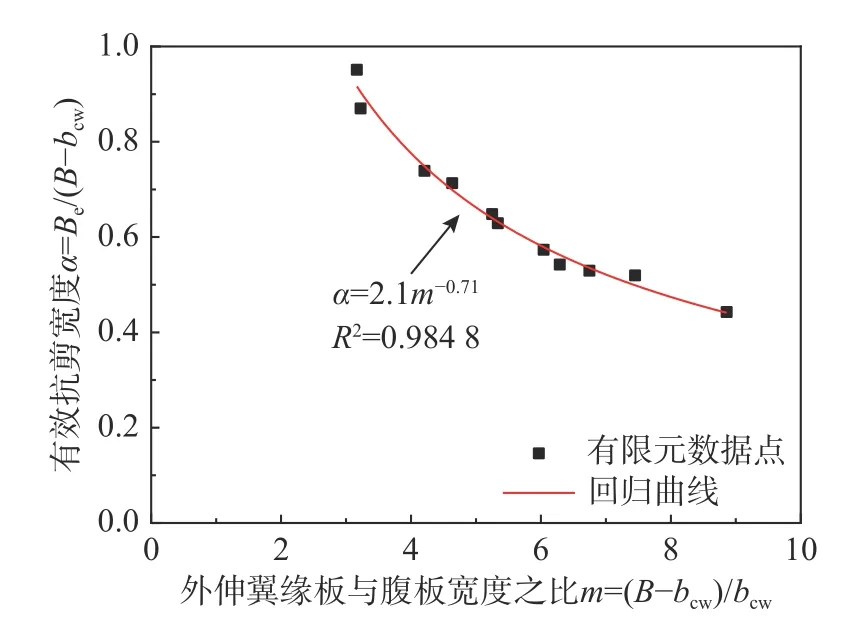
图19 外伸翼缘板有效抗剪宽度α的回归曲线Fig. 19 The regression curve of α
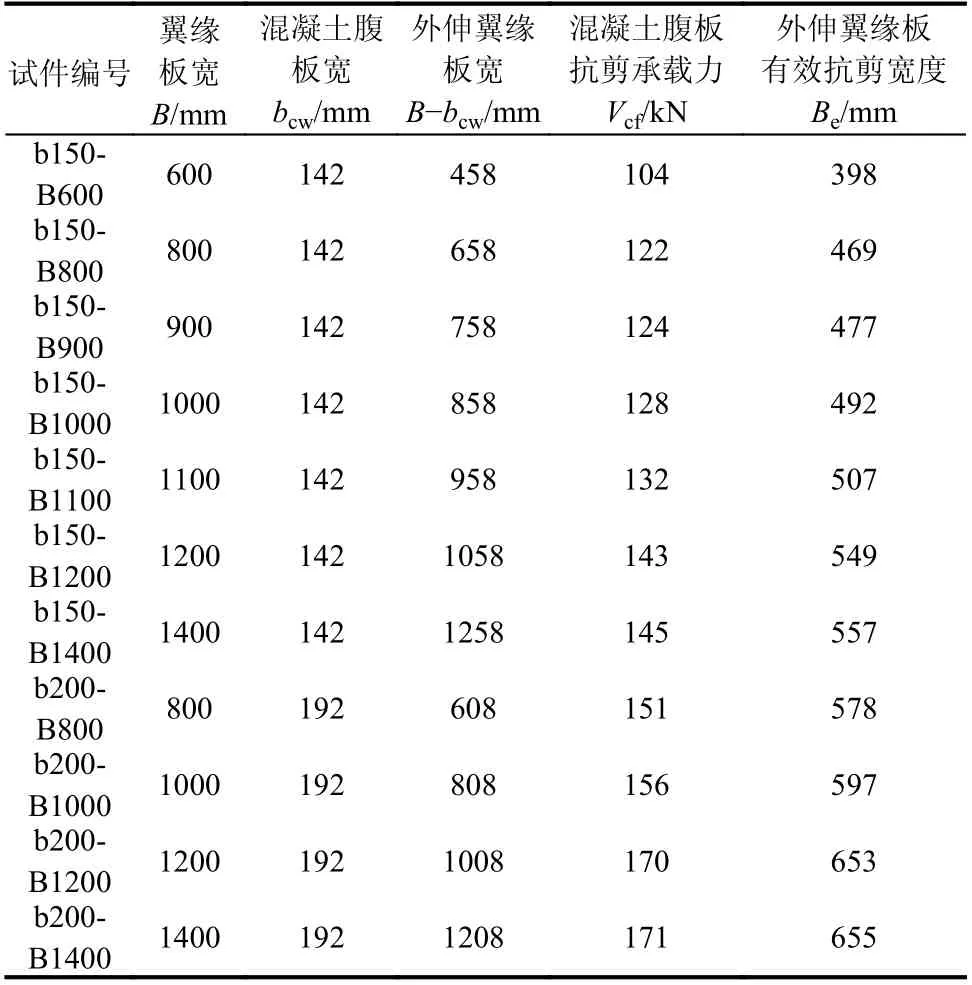
表6 外伸翼缘板抗剪承载力和外伸翼缘板有效板宽Table 6 Model parameters and shear capacity
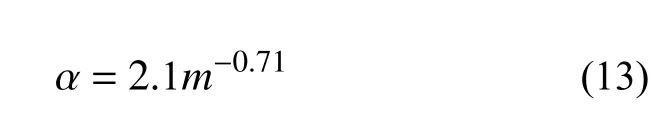
根据以上分析,本文提出考虑外伸翼缘板有效抗剪宽度系数α的混凝土抗剪承载力计算公式:

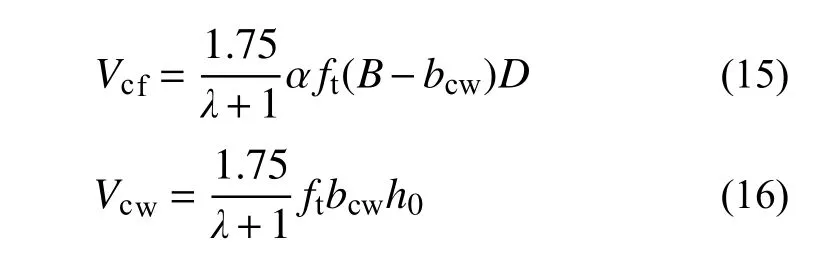
式中,h0为混凝土截面腹板有效高度。
将混凝土、U形钢腹板、纵筋销栓作用三部分的抗剪贡献叠加,最终得到WUSCB抗剪承载力计算值,如表7所示。依照本文计算方法得到的组合梁抗剪承载力与试验值吻合良好,平均值为1.02,标准差为0.07。其中,试件CB-7-HP因在内部混凝土设置箍筋,抗剪承载力试验值略大于计算值,但未达到按照式(10)进行计算的钢筋混凝土内箍筋的承载力,因此建议忽略试件箍筋的承载力贡献。
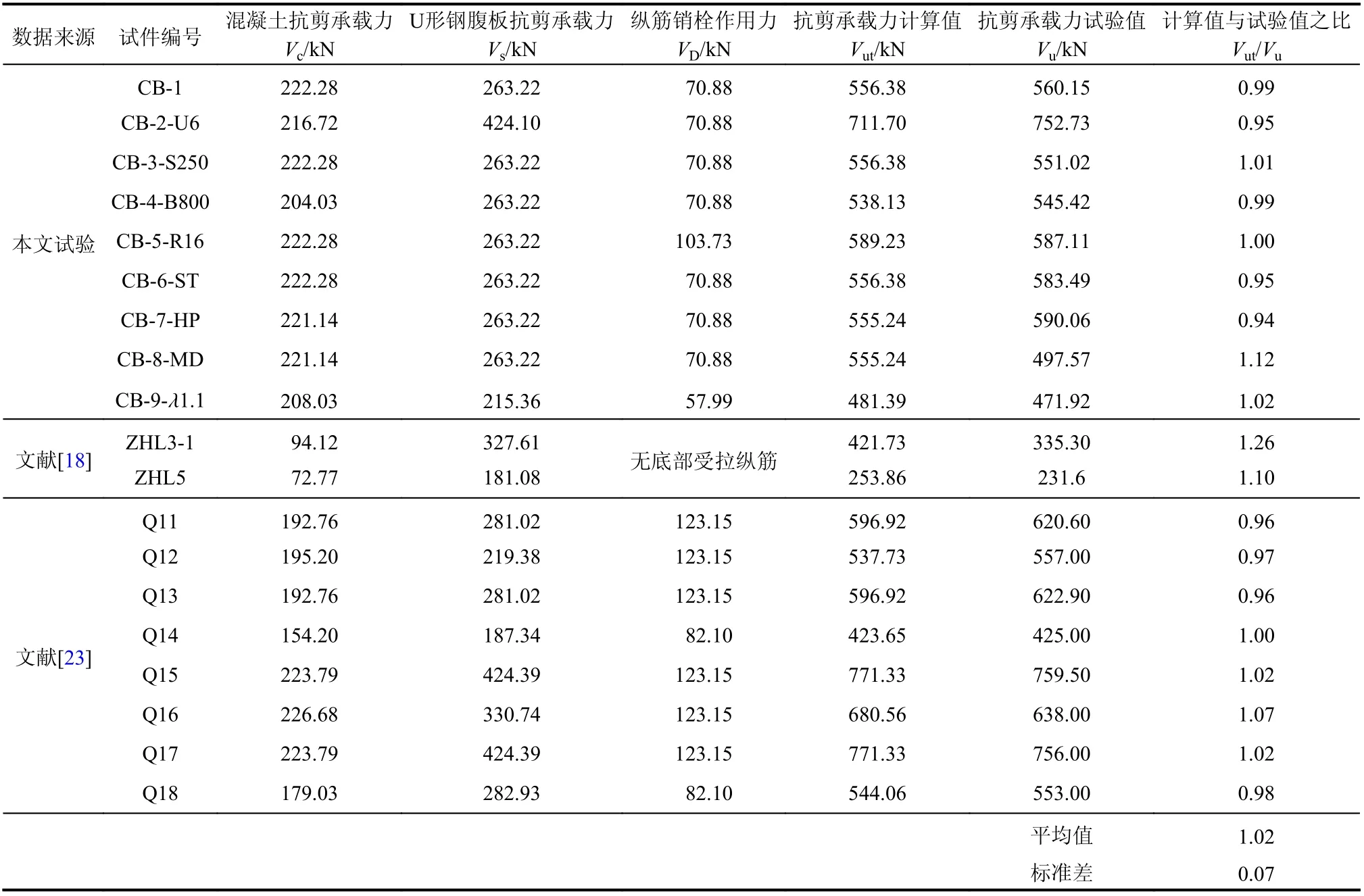
表7 抗剪承载力设计方法验证Table 7 Verification of design method of shear capacity
为进一步验证所提出的抗剪承载力设计方法的适用性,本文提取了文献[18]和文献[23]中发生剪切破坏的外包U形钢-混凝土组合梁试件试验数据,利用式(7)计算两种组合梁的抗剪承载力并与其试验值进行验证,其结果如表7和图20所示,对比发现对于不同抗剪连接件的外包U形钢-混凝土组合梁,在满足完全抗剪连接的基础上,本文所提出的抗剪承载力设计方法仍然具有较好的吻合程度,说明该设计方法的适用性较好。
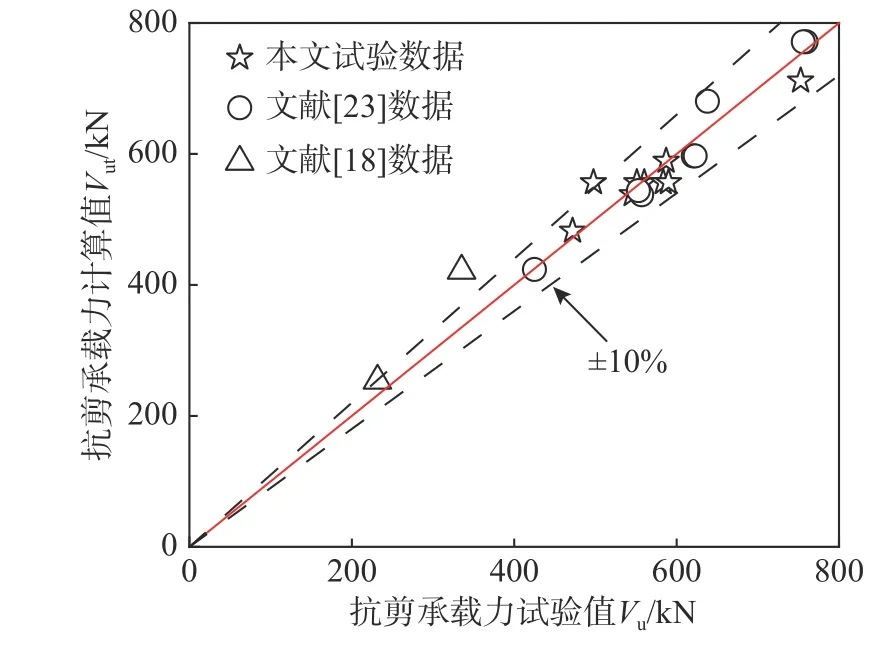
图20 抗剪承载力计算值与试验值对比Fig. 20 The comparison between the calculated capacity and test capacity
5 结论
通过对9个腹板嵌入式外包U形钢-混凝土组合梁的剪切性能试验研究以及有限元参数分析,提出组合梁的抗剪承载力设计方法,得出以下主要结论:
(1) WUSCB试件典型破坏过程分为线弹性段、弹塑性段和荷载下降段。在剪跨比λ=0.9、λ=1.1时,所有试件整体上均发生斜压破坏,混凝土翼缘板表现出斜截面剪切和端部冲切两种破坏现象。
(2) WUSCB试件具有良好的刚度和承载力,试件的延性系数µ=9.56~27.22,表明即使发生斜压破坏,其延性仍然较好;塑性发展系数γs=1.22~1.67,表明试件在屈服后仍有较大的抗剪承载储备。
(3) U形钢壁厚和剪跨比直接影响WUSCB的抗剪承载力;梁底纵筋直径和栓钉的设置对抗剪承载力影响不大,但能提高延性;在满足完全抗剪连接的前提下,适当增大燕尾形连接件间距能提高组合梁延性;当混凝土翼板宽度超过有效抗剪宽度时,继续增大板宽会降低延性。
(4) 提出了WUSCB的抗剪承载力设计方法,该方法同时考虑U形钢腹板、底部纵筋销栓作用和混凝土三部分的抗剪贡献,能较准确地预测WUSCB的抗剪承载力,且对不同抗剪连接件形式的外包U形钢-混凝土组合梁均具有较好的适用性。
