基于物理机制的随机地震动场中供水管网抗震功能反应分析
2022-07-04缪惠全
缪惠全,李 杰
(1. 北京工业大学城建学部,北京 100124;2. 北京工业大学城市与工程安全减灾省部共建教育部重点实验室,北京 100124;3. 同济大学土木工程学院,上海 200092;4. 上海防灾救灾研究所,上海 200092)
由于受到震源的物理机制、地震波传播途径和工程场地条件等因素的影响,工程场地地震动表现出了明显的随机性。为了准确地反映工程系统的地震反应信息,特别是结构响应的随机涨落特征,需要对系统进行随机地震反应分析。
埋地管线随机地震反应分析最早可以追溯到Hindy和Novak[1]在1980年的工作,此后,一些学者进一步考虑地震动的非平稳性、空间相关性等因素对地下管线进行了随机地震反应分析[2−3]。近些年来,一些特殊位置或者特殊形状的管线的地震反应引起了研究者的重视,如海底管线[4−6]、地下综合管廊内的管线[7]、场地土随机组合的管线[8]、异型管线[9]等。
随机地震动场中供水管网抗震功能反应分析事实上涉及如下四个方面的工作。首先,供水管网所面临的“外因”,即随机地震动场模型,恰当的地震动场模型是实现正确进行供水管网功能分析的基础。总体而言,地震动场模型可以分为两类:一类是非条件模拟,其一般做法是利用功率谱模型和相干函数模型来生成地震动时程,幅值的非频稳性主要是通过施加经验的包络函数实现,代表性的方法是Hao等[10]提出来的HOP方法;第二类则是条件模拟算法,其中最著名的就是Vanmarcke等[11]提出的,通过改进传统的Kriging方法而得到的多变量线性预测方法(multivariate linear prediction method,MLP method)。其次,则是埋地管网地震反应分析模型。该领域常见的分析方法包含了经验统计方法、共同变位法、反应位移法(拟静力分析)、波动分析法(动力分析)、有限元方法、有限元和离散元相结合的方法等。经验统计法适用性有限,而共同变位法与反应位移法因为简单实用则分别是美国ALA生命线工程协会[12]和日本管道协会[13]推荐规范所采用的方法,有限元方法以及有限元、离散元相结合的方法,则更多用于管线在滑坡、断层作用下的大变形分析,计算相对复杂。再次,供水管网抗震功能分析不能脱离随机动力系统的分析方法,常见的方法如矩方法、蒙特卡洛模拟法,除此之外还有大量比较小众的方法,如与机器学习相结合的蒙特卡洛模拟法[14]、与管理学相结合的基于Agent模型的方法[15]、解析图论法[16]、复杂网络指标法[17]、概率图模型[18]、熵函数法[19]等。其中,由李杰和陈建兵[20]所提出和发展的概率密度演化方法,近些年来引起了领域研究者的重视,并成为国内外流行的方法之一,在随机系统动力分析、结构振动控制、生命线地震工程等领域得到了应用和推广。最后,则涉及到供水管网功能分析的问题。目前,常见的功能分析方法为稳态流方法,该方法计算简便,但无法反应管内流体动态变化的情况,也就是说,一般管网所谓功能动态分析,其时间“t”这一物理量是虚拟的。将瞬变流引入管网抗震功能的动态分析,是笔者进行的重要尝试,本论文将其进一步拓展至随机动态功能分析。
针对供水管网的地震反应分析而言,既有研究存在三个主要的问题:1)忽略了管网拓扑结构的影响,分析目标只是单独的管线,而非具有复杂结构的地下管网;2)经典的随机振动分析方法主要用于线性体系的随机地震反应分析,难以用于非线性系统的随机振动反应分析;3)仅考察管线结构的地震响应而未能落实到管网的功能性分析之上,特别是不能反应管网供水功能动态变化的过程。
因此,本文在进一步修正工程场地地震动随机场物理模型[21]的基础之上通过引入埋地管网地震反应分析模型[22],结合概率密度演化方法[23−24],实现了具有非线性特性的埋地管网的随机地震反应分析;进而,结合管网流体的瞬变流分析理论实现了城市供水管网的随机功能分析。从而建立了“工程场地随机地震动场模拟→管网系统随机地震反应分析→渗漏供水管网动态水力分析→供水管网随机功能反应分析”这一完整的分析路径,实现了基于物理机制的随机地震动场中城市供水管网随机功能反应分析。
本文工作的创新性在于其不仅可有效分析具有复杂拓扑结构的地下管网结构,而且将管网结构的破坏落实于管网供水功能的分析之中;其次,本文首次将时间“t”这一物理变量引入震时供水管网的抗震功能分析之中,真正实现了供水管网的动态抗震功能反应分析。
1 地震动随机场的物理模型
工程场地随机地震动场的模拟是地震工程领域的基础性课题,同本文所研究的问题相比,也是一个相对独立的问题,为此,笔者所在的团队进行了系列的探索和尝试,代表性成果如文献[21, 25 − 28]。本文中所采用的模型是在文献[21]的基础上进行了进一步的修正,其基本的思路是修正了地震波在局部工程场地中频域内的幅值传递函数和相位传递函数,以进一步反应地震波在局部工程场地中传播的相位频散特性。
工程场地地震动随机场的物理模型可表述为[21]:

式中:aRS(rl,t)为场地内任意一点地震动;rl为场地内任意一点沿波的传播方向上到场地入射点的距离;t为时间;ARS(ξs,ω)为场地地震动模型的傅里叶幅值谱;ΦRS(ξs,ω)为模型的相位谱[26],参数向量ξs=[ξ,α0,cg]=[A0,τ,ξg,α0,cg]是一个六维的随机向量,其分布信息可以参考文献[29]。
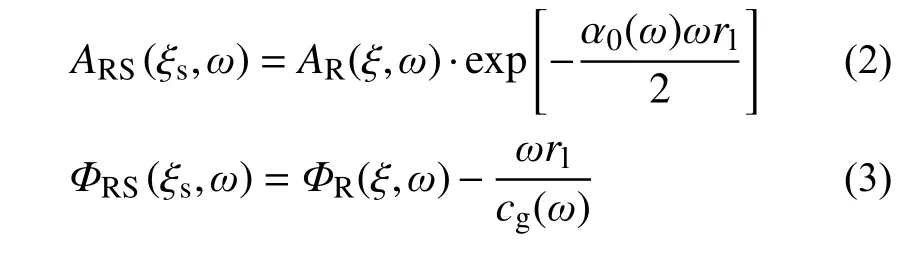
为了进一步反映地震动场中地震传播的相位频散特性,上述模型修改为:式中:AR(ξ,ω)为工程场地地震动模型的傅里叶幅值谱;ΦR(ξ,ω)为相位谱;而反映场地内地震波传播特性的随机参数α0和cg取为随圆频率ω改变的函数,其具体的形式为:
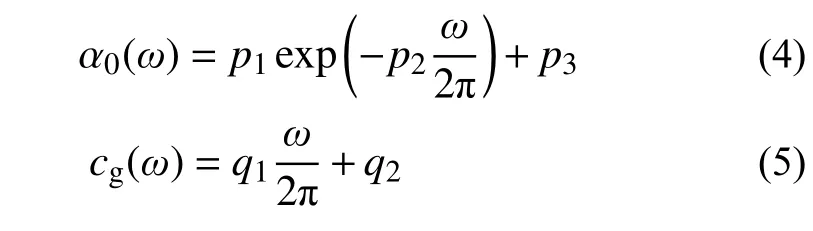
式中,参数p1、 p2、 p3、q1、 q2为模型中的随机参数,其具体的信息可以根据SMART-1地震动台阵所测地震动信息进行统计建模,此处仅给出其结果,如表1所示。
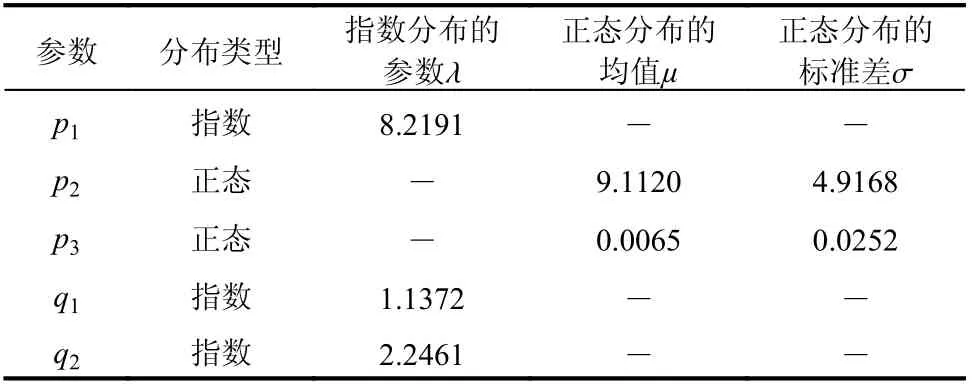
表1 地震动场随机参数分布信息Table 1 Random parameter distribution information of ground motion field model
2 埋地管网地震反应分析模型
地震作用下埋地管线可以简化为弹性地基梁模型,若忽略管线的动力效应,其轴向和横向的控制方程可以表示为[11]:
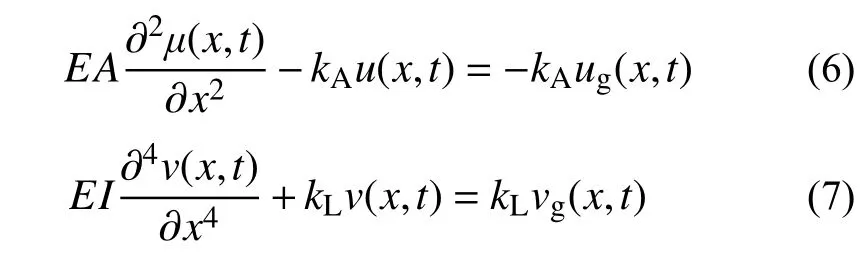
式中:E为管材的弹性模量;A为管线的横截面面积;u(x,t)和v(x,t)分别为管线的轴向和横向位移;kA和kL为管周轴向和横向的土弹簧系数;ug(x,t)和vg(x,t)分别为输入地震动的轴向和横向位移。
将地下管线简化为弹性地基梁模型是管线地震反应分析的常用方法,如文献[4, 8]。不同于地上结构,地震作用下地下结构的惯性力不明显,地下结构通常可采用拟静力方法进行分析,如文献[12, 30 − 31]。弹性地基梁模型无法反应管线管壁的屈曲等复杂行为,而惯性力的忽略,则可能低估管线的地震反应,特别是大管径、高密度材质管,但已有的分析表明:这种动力影响是非常微弱的[32−34],这是地下结构进行拟静力分析的基础。
对管线进行单元划分,并以轴向弹簧和转动弹簧模拟管段之间的接头连接,根据有限单元法,可以建立整个埋地管网的系统运动控制方程为[22, 30]:

式中:u为管线单元节点位移向量;ug为地面位移荷载向量;KSYS为系统的总刚度矩阵,可以表达为:
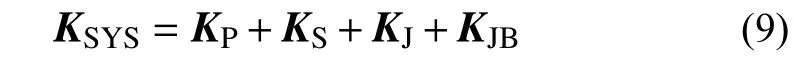
KL为系统荷载转化矩阵,可以表达为:

式中:KP为管线单元刚度矩阵;KS为土弹簧单元刚度矩阵;KJ为接头单元刚度矩阵;KJB为边界连接单元刚度矩阵。
求解式(8)可以得到管网系统任意单元的地震响应。若单元i为接头则可以得到其轴向变形为:
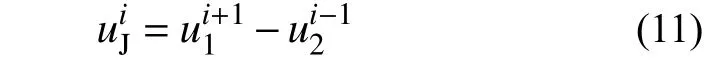
接口相对转角为:

3 基于瞬变流的渗漏管网功能分析
供水管线中一维瞬变流的运动方程和连续方程分别为[35−36]:
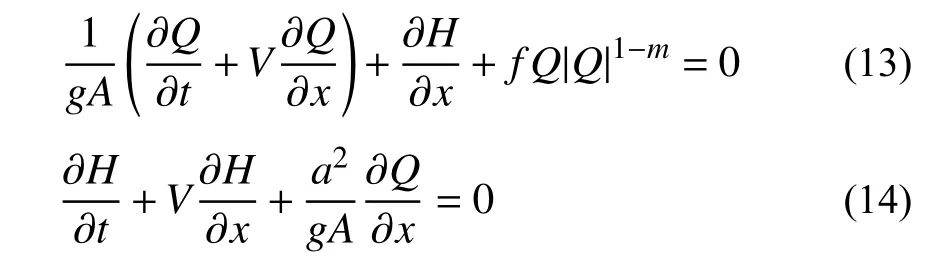
式中:Q/(m3/s)为管线中流体的流量;V/(m/s)为流体速度;H/Pa为流体压力;f为摩阻系数;m为流态指数,二者都与摩阻损失(沿程损失)有关的参数,与选择的沿程阻力损失计算模型有关;a/(m/s)为小扰动在管内流体中的传播速度,可以表达为:
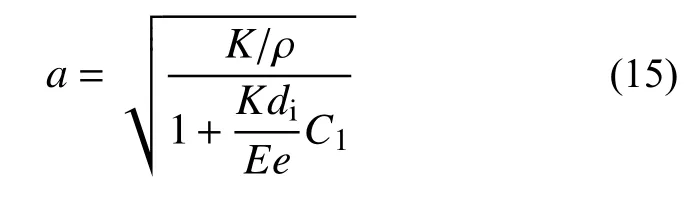
式中:K/Pa为流体的体积模量;ρ/(kg/m3)为流体的密度;di/m为管道的内径;e/m为管道的壁厚;C1为与管道两端支撑情况有关的常数。
可采用特征差分方法求解上述偏微分方程组[35 − 36]。
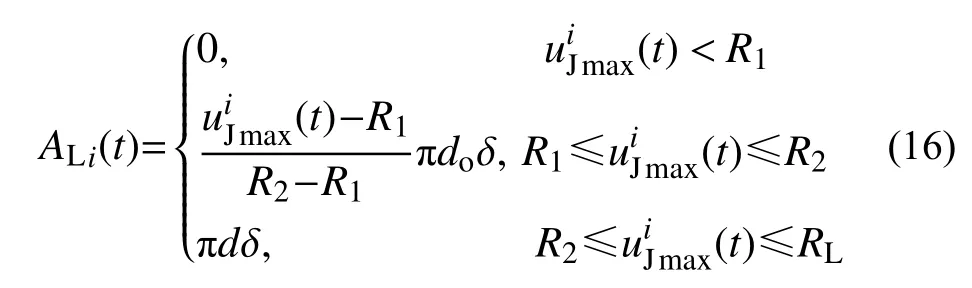
地震作用下管线中某一个接头i其渗漏面积可采用如下的计算方法[37]:式中:do为管线的外径;δ为接头缝隙的最大宽度;RL为接口插头插入承口的深度,对灰口铸铁管,三者参数值可以参考文献[38],对于球墨铸铁管,则可参考文献[39];R1和R2为接头的弹性变形和塑性变形极限值,文献[40]给出了不同类型接头R1和R2的统计值,文献[41]也可作为有效参考。max(t)为管线接头受拉变形的历史最大值,其定义为:
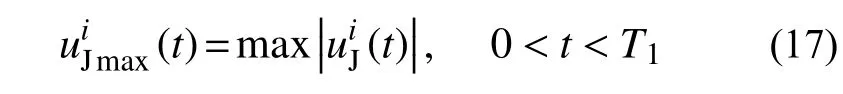
式中,0~T1为地震发生的起止时刻。
为了简化计算,一根管线处的渗漏面积可以集中到管网中该管线的两端节点处[42],因此,管网中某一节点j的总渗漏面积为:
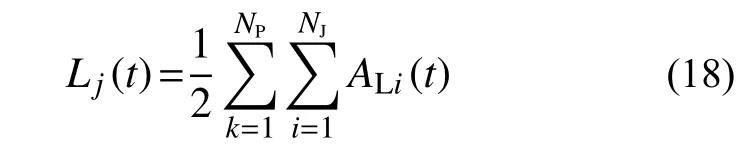
式中:NJ为管线k上的接头数;NP为管网中节点j所连接的管线总数。则在管线的渗漏点处,渗漏量与渗漏点处水压的关系可以表示为[37]:
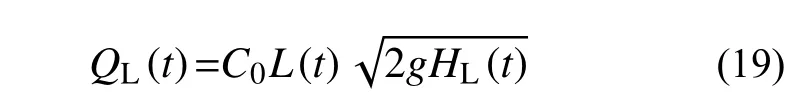
式中:QL(t)为渗漏点处的渗漏量;L(t)为渗漏面积;HL(t)为渗漏点水压;g为重力加速度;C0为渗漏模型参数,对刚性接头,C0参数可以取值0.06~0.12,对于柔性接头,C0参数可以取值0.03~0.06。
将式(19)引入式(13)与式(14)中,即可求解带有渗漏的供水管网水压和流量,以及渗漏量的变化情况。
4 供水管网随机功能反应分析
为了考察随机地震动场中具有非线性特性的城市供水管网的抗震功能,此处引入概率密度演化理论进行分析[23−24]。
4.1 概率密度演化理论的物理基础
一般情况下,工程结构的非线性随机动力响应分析的基本物理方程可以表述为[20]:

为了实现基于物理机制的随机地震动场中城市供水管网随机功能反应分析,建立“工程场地随机地震动场模拟—管网系统随机地震反应分析—渗漏供水管网水力分析—供水管网随机功能反应分析”这一完整的分析路径,当地震动场模型中的随机变量为Θ时,可以根据式(1)~式(5)得到随机的地震动场A(Θ);进而,当选取供水管网的接头变形作为随机分析考察的状态量时,根据概率密度演化理论,此时系统的物理方程即为式(8),若记接头变形为R(t),则考虑随机因素影响的接头变形为R(Θ,t),则系统的广义概率密度演化方程为:

求解式(22)则即可得到管网系统接头的随机地震反应。而当选取供水管网节点水压作为随机分析考察的状态量时,系统的物理方程即为式(13)和式(14),若记管网节点水压为H(t),则考虑随机因素影响的节点水压为H(Θ,t),则此时系统的广义概率密度演化方程为:
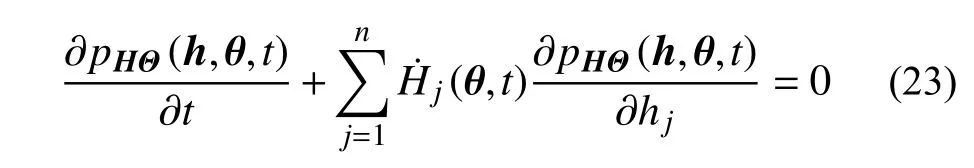
求解式(23)则可得到管网系统节点水压的随机反应。该偏微分方程的边界条件为:

4.2 广义概率密度演化方程的求解步骤
1)对原始概率空间进行合理剖分并选取代表点并确定其赋得概率;
2)数值求解物理系统式(20),在本文中即表现为求解埋地管网的地震响应,并根据管线的破坏状态,求解管网动态水压、流量、渗漏量等物理信息,从而给出{Θ=θ}时广义概率密度演化方程的广义速度解答(θ,t);
3)求解广义概率密度演化方程;
4)计算物理过程X(t)的概率密度函数为:

5 算例
以一小型供水管网为例对管网在随机地震动场中进行功能分析。该管网为一个小型虚拟供水管网:一方面,其包含了供水管网常见的管线类型,如直管、弯管、T型管、十字型管等;另一方面,其具有管网水力分析代表性的环状和树状结构。因此,该案例具有非常好的代表性。
管网的拓扑结构、管线和节点标号信息如图1所示,管线的几何和材料信息如表2所示,其中:Lp为管线的长度;do为管道的外径;di为管道的内径;R1和R2为管线接头弹性变形和塑性变形的极限值。管材均为灰口铸铁管,管段长度6 m,管材弹性模量为1.50×1011Pa,泊松比0.3,管网处于II类场地,埋深1 m,场地土为中密度粘性土,其不排水抗剪强度为22.93 kPa,因此,轴向和横向土弹簧系数可以根据ALA规范[12]取得,并如表2所示。
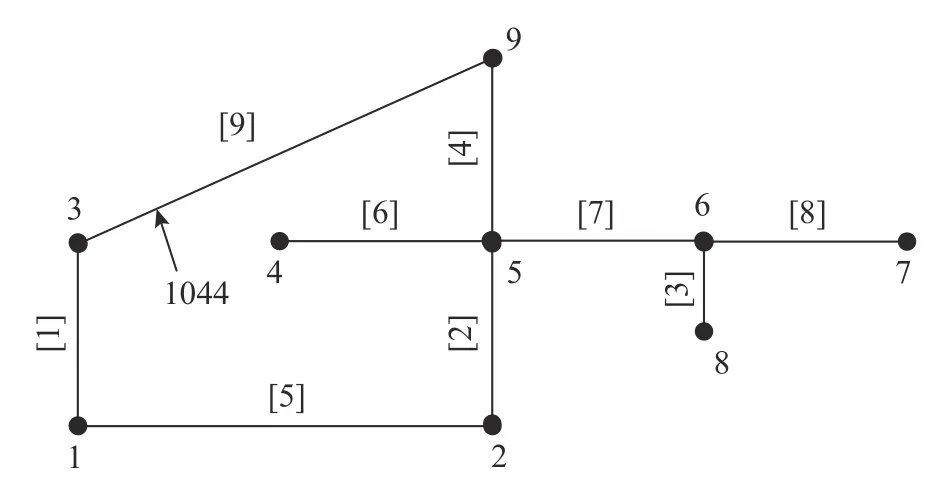
图1 供水管网Fig. 1 Water supply network
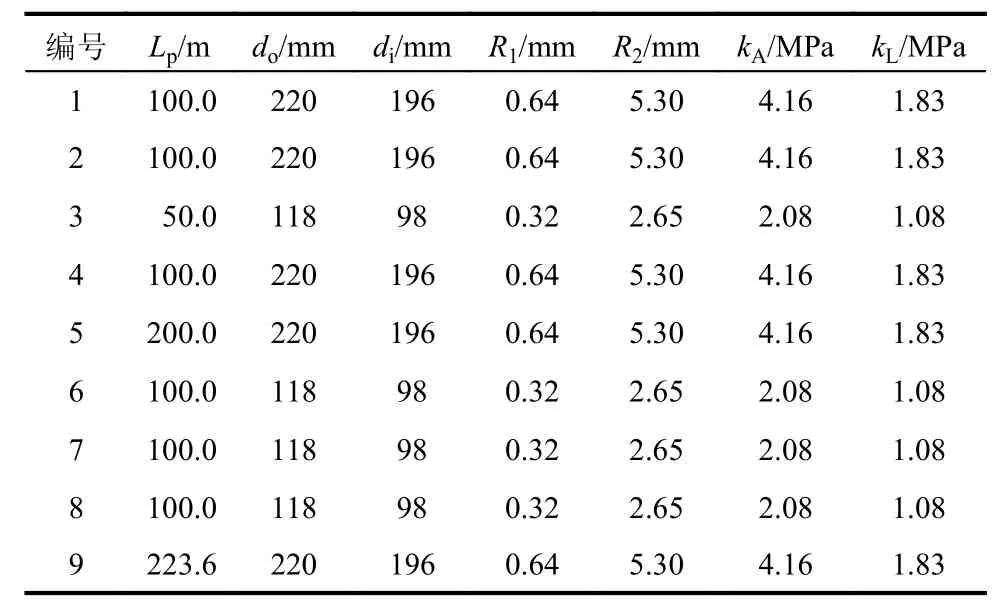
表2 管网中各管线信息Table 2 Information of pipelines in network
5.1 随机地震动场
根据本文第1节介绍的工程场地地震动随机场的物理模型,可用基于GF偏差的随机选点法选取300个样本点[43],每个样本点的维度为9维。该方法由杨俊毅等[44]提出,其中GF偏差的含义为广义F偏差,即Generalized F-discrepancy,是一种针对随机动力系统分析的点集优选策略。据此可生成300个不同的地震动场。假设管网抗震设防烈度为8度(相应的设计地震峰值加速度0.2 g),地震入射角度为45°,持时16 s,不同样本入射方向上相距100 m的两点地震动位移如图2所示。
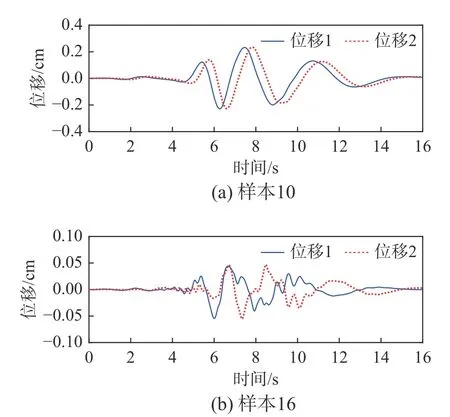
图2 地震动场位移时程曲线Fig. 2 Displacement history data in seismic field
5.2 管网随机地震反应分析
按照本文第2节所提出的埋地管网地震反应分析模型,可以得到管网在各个地震场样本中的反应,包括接头变形和管体应变等信息。进而根据概率密度演化理论可以得到管网的随机地震反应。此处以9号管线编号为1044的接头为例给出其计算结果(接头1044位置如图1所示,为距管网3号节点第7根管段和第8根管段连接处)。其中,LW和TVD两种算法得到的接头1044的300个样本点的均值和均方差如图3所示,其代表性时刻的概率密度曲线如图4所示,其变形的概率密度演化曲面和概率密度等高线线如图5所示。
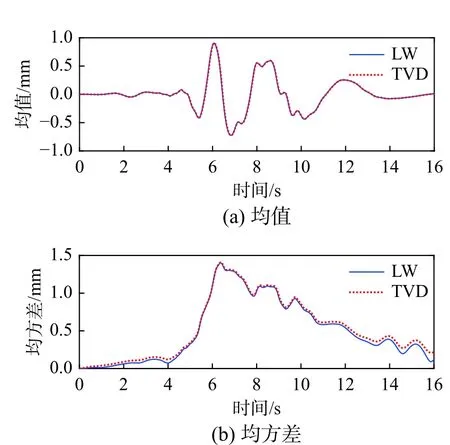
图3 接头1044的均值和均方差Fig. 3 Mean and standard deviation of joint 1044

图4 接头1044典型时刻的概率密度曲线Fig. 4 Probability density curve at typical moment of joint 1044
从图5可以看出,管网地震反应在随机地震动场中呈现显著的随机性,其地震响应的概率密度随时间的演化具有显著的随机涨落特征。
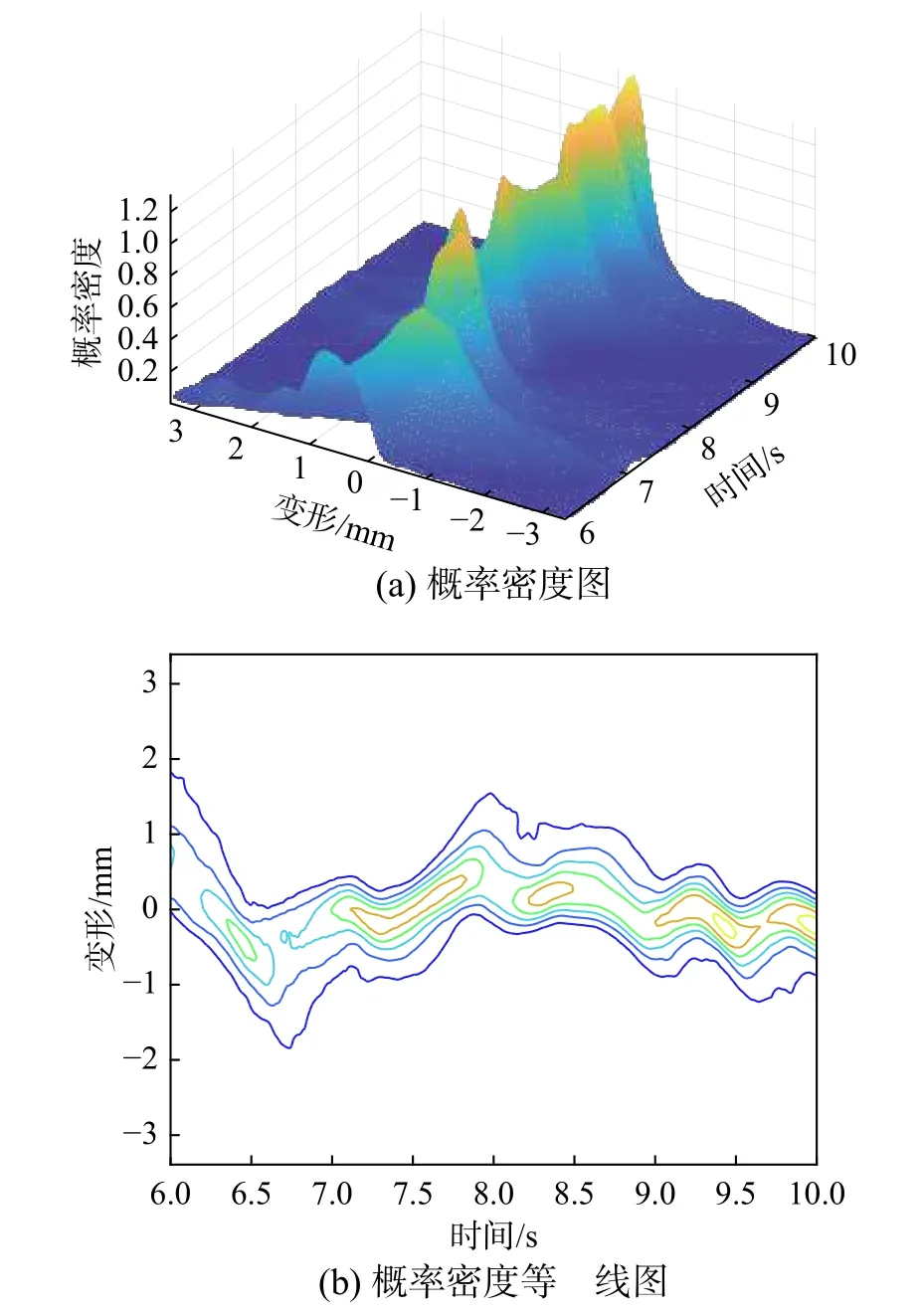
图5 接头1044的概率密演化图和概率密度等高线图Fig. 5 Probability density evolution map and probability density contour map of joint 1044
对应的,也可以得到管网的破坏情况。根据本文前述提出的渗漏面积计算模型,则根据接头的变形情况可以得到整个管网各个节点处的破坏面积。此处仍给出样本10和样本16处节点5处渗漏面积随时间的变化情况如图6所示。从图6也可发现,正是由于地震动场的随机性,管网的破坏过程和最终的破坏结果也呈现显著的差异。

图6 节点5处的渗漏面积Fig. 6 Leakage area at node 5
5.3 震时供水管网功能分析
管网中各节点的几何信息如表3所示,此处假定节点1为定压节点,水压为40 m。各管线的水力摩阻系数f和m均为2.7和0.125。重力常数g为9.806 m/s2,水的弹性体积模量K为2.2×109N/m2,密度ρ为998.2 kg/m3且渗漏模型中渗漏系数C0为0.09。定义动态水力计算时间为25 s,即地震后仍持续观测9 s,计算时间间隔Δt=0.01 s。按照本文第4节的方法计算,即得到整个管网在不同地震动场样本的动态水力。图7和图8给出了样本10和样本16管网节点7处的节点水压和渗漏量变化时程曲线,从图7和图8可以看出,随机的地震动场中管网的供水功能和渗漏量也呈现显著的差异。

表3 管网中各节点信息Table 3 Node information in network

图7 节点7处不同样本水压值Fig. 7 Water pressure of different samples at node 7
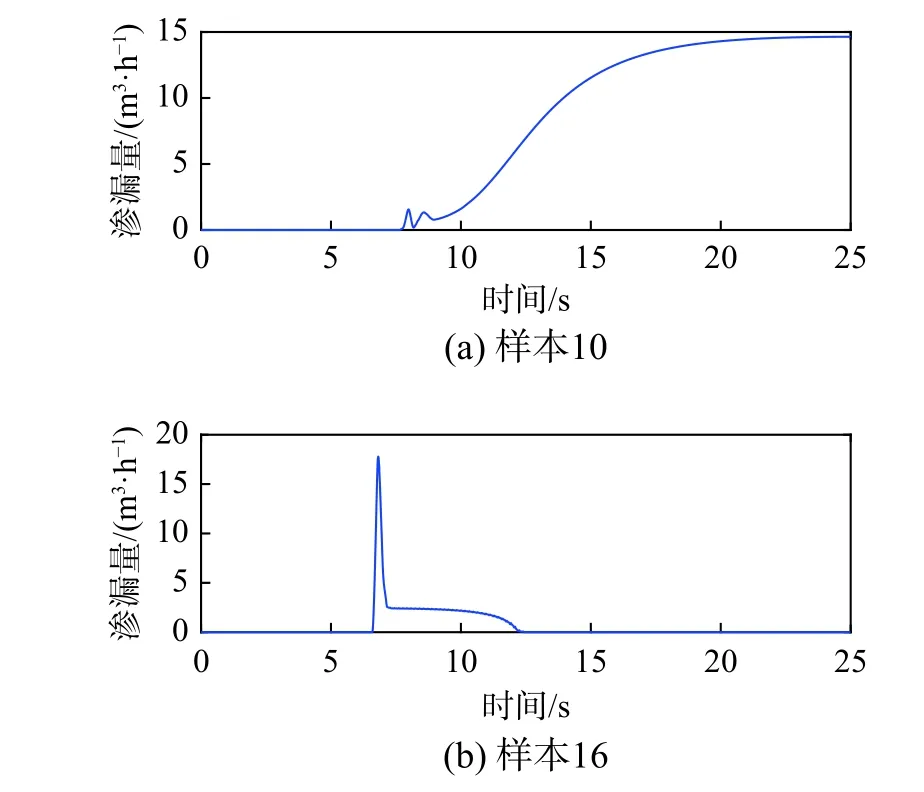
图8 节点7处不同样本渗漏量Fig. 8 Water leakage of different samples at node 7
进一步根据概率密度演化方法计算管网各节点水力、流量和渗漏量的概率密度信息。此处以管网的节点7为例,其水压的概率密度演化图和概率密度等高线图如图9所示,其渗漏量的概率密度图和概率密度等高线图如图10所示。
从图9可以看出,管网节点水压的概率密度呈现明显的演化特征,特别是在6 s~8 s,也就是地震动最剧烈的时间段,这表明管网的随机结构响应最终落实到管网功能的随机性。从图10可以看出节点7处的渗漏量随时间的变化也呈现显著的随机涨落特征,特别是在8 s左右,渗漏量的概率密度峰值显著降低分散化,并最终逐渐趋于稳定。
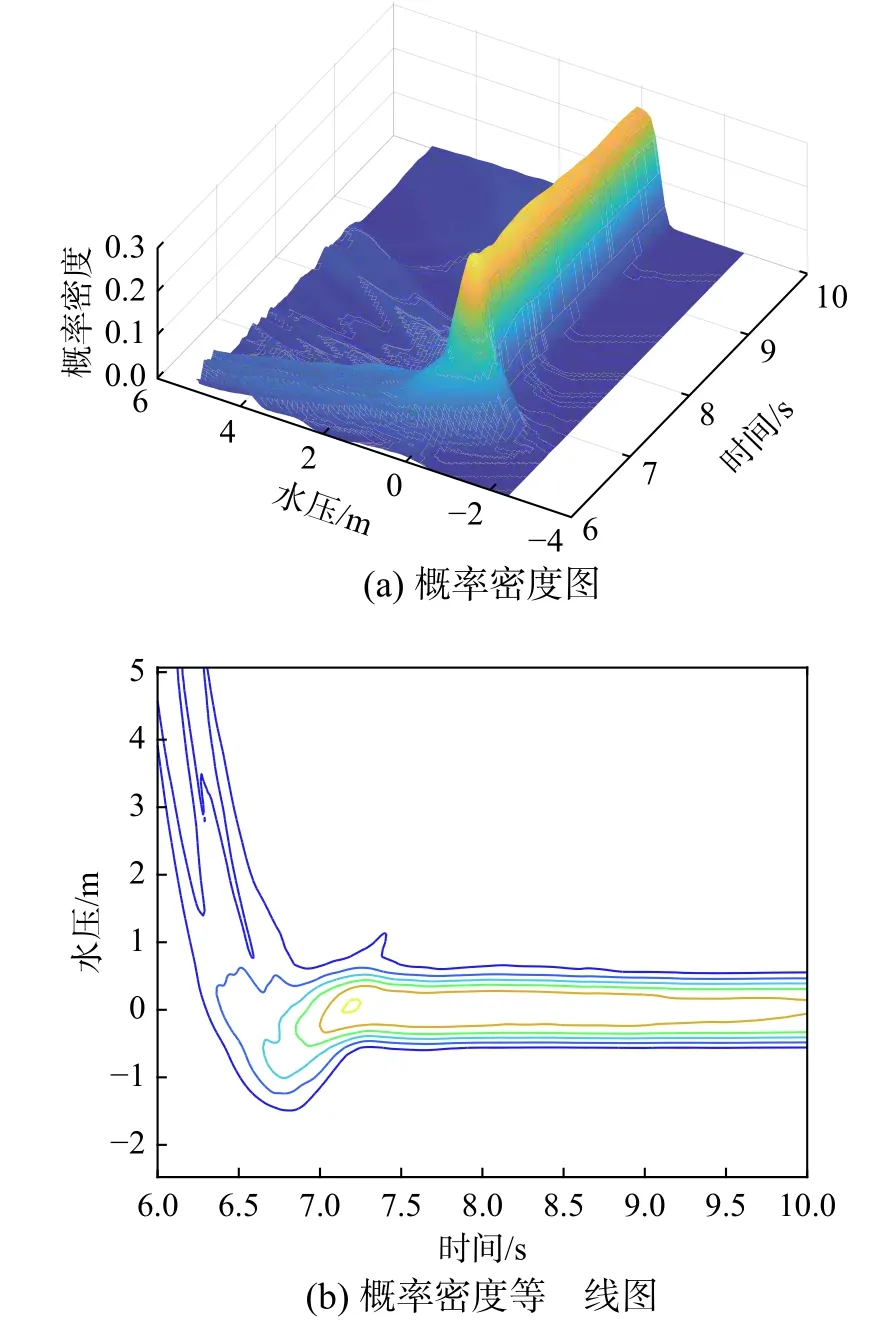
图9 节点7处水压概率密度图和概率密度等高线图Fig. 9 Probability density map and probability density contour map of water pressure at node 7
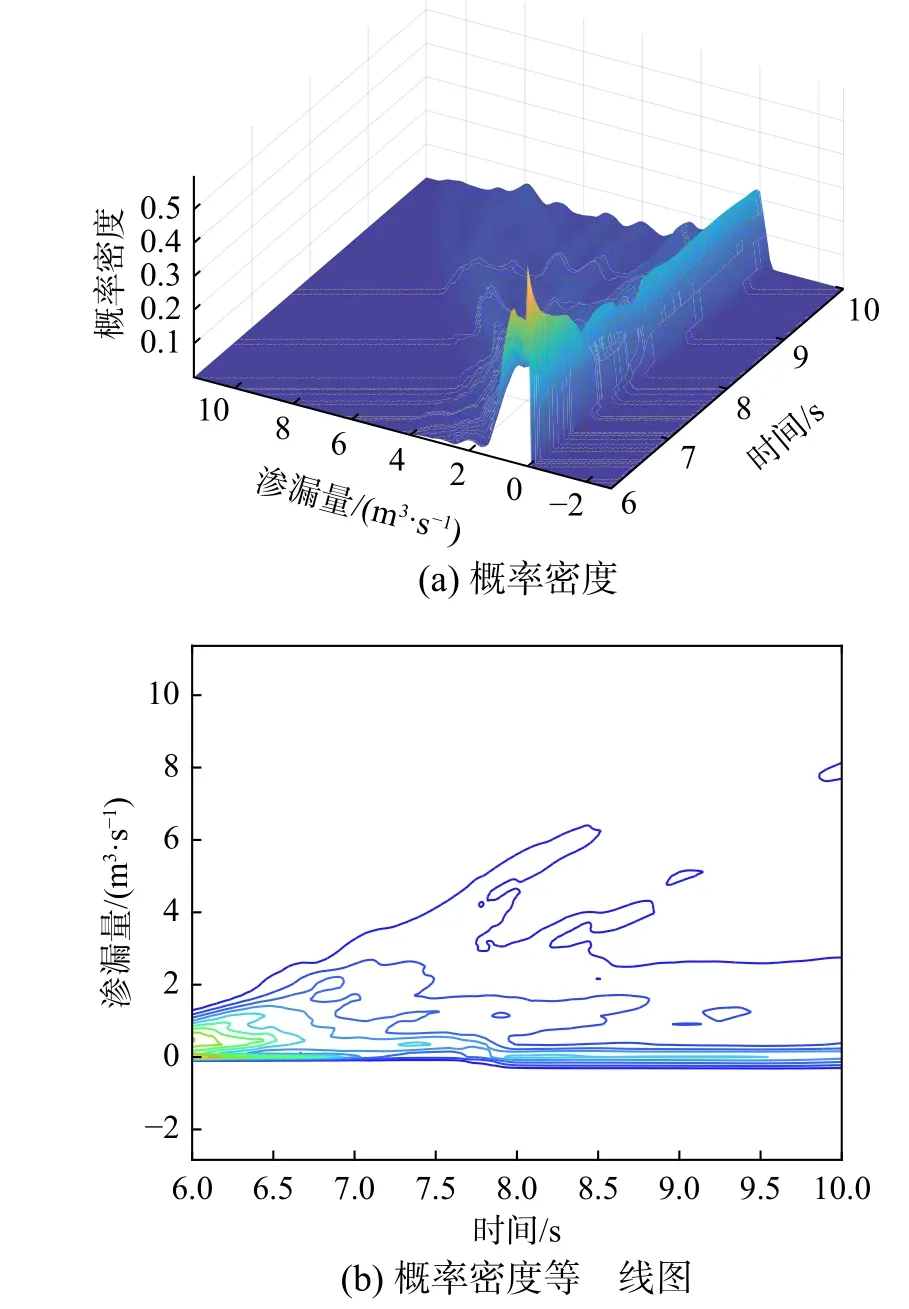
图10 节点7处渗漏量概率密度图和概率密度等高线图Fig. 10 Probability density map and probability density contour map of leakage at node 7
节点7处水压、渗漏流量的均值和标准差分别如图11和图12所示。从图11和图12不难发现,在强震到来之前(0 s~5 s),管网基本维持正常功能状态,如3 s时节点7处的水压均值为10.09 m,渗漏量也非常小,均值0.015 m3/h。随着强震阶段到来,该节点处的功能在不同的样本中出现了显著的变化,但是在总体上,节点7处的水压呈现先降低后升高的现象,破坏稳定后的水压平均值维持在3.79 m,而渗漏量则维持在3.117 m3/h。节点7处水压在平均程度上降低了70.47%。
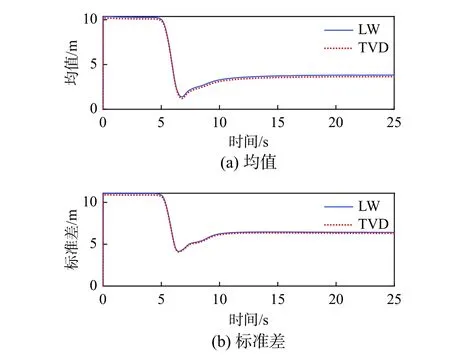
图11 节点7处水压的均值和标准差Fig. 11 Mean and standard deviation of water pressure at node 7

图12 节点7处渗漏量的均值和标准差Fig. 12 Mean and standard deviation of leakage at node 7
6 结论
本文在修正工程场地地震动随机场物理模型的基础之上通过引入埋地管网地震反应分析模型,结合概率密度演化方法实现了具有非线性特性的埋地管网的随机地震反应分析;进而,利用瞬变流分析理论实现了城市供水管网的随机抗震功能分析;最终建立了“工程场地随机地震动场模拟→管网系统随机地震反应分析→渗漏供水管网动态水力分析→供水管网随机功能反应分析”这一完整的分析路径,实现了基于物理机制的随机地震动场中城市供水管网抗震功能反应分析。算例表明:
(1)不同的地震动场中,管网的破坏过程、最终的破坏结果和抗震功能,均呈现显著的差异。以本文算例为例,在样本10中,管网节点5处的渗漏面积是分阶段的增加至0.022 m2,而在样本16中,管网节点5处的渗漏面积则是以较快的速度单调增加至0.062 m2。类似地,前者水压是先降低至−1.69 m又逐渐增加至3.19 m;而后者则是先降低至−3.68 m并恢复至0 m而维持基本不变。显然,这体现了随机的地震动场对管网破坏过程和结果的影响。
(2)在随机地震作用下,管网的地震响应、节点水压和渗漏量都呈现显著的随机涨落特征。当管网破坏状态稳定以后,管网的节点水压和渗漏量,也逐步达到稳定的状态。本文算例量化的呈现了这一动态变化过程。以节点7处的动态水压为例,在地震动最剧烈的时间段6 s~8 s,其概率密度分布呈现显著的变化;而该节点处的渗漏量,也呈现随时间变化随机涨落的特征,特别是8 s左右,渗漏量的概率密度峰值显著降低分散化,并最终逐渐趋于稳定。当然,在不同类型的地震动场或不同类型的管网,管网节点水压和渗漏量的概率密度的变化时刻和特点可能会有所不同,但本文所提的方法可以有效地量化地揭示这一过程,这在之前对供水管网抗震功能的分析中是尚未实现的。
本文的工程应用价值在于:一方面,本文模型更加契合工程实际,它不仅可以有效反应地震作用下具有复杂拓扑结构的地下管网的地震响应,奠定管线抗震设计的基础,更重要的是,它将管网结构的物理响应落实于供水管网的功能分析中[45−46],从而为基于功能的供水管网抗震设计奠定了基础;另一方面,本文模型真正实现了管网功能的动态随机地震反应分析,时间“t”在系统的功能分析中具有明确的物理意义,从而为管网功能的分析预测与系统的动态监测分析相结合奠定了基础。
