基于极限平衡理论的钢与混凝土组合框架结构抗震分析

2022-07-04王玉良郝际平姜维山

工程力学 2022年7期

王玉良，赵敏，郝际平，薛强，姜维山

(1. 天津城建大学天津市土木建筑结构防护与加固重点实验室，天津 300384；2. 西安建筑科技大学土木工程学院，西安 710055)

钢与混凝土组合框架结构是指含有钢与混凝土组合构件的框架结构，通过钢与混凝土的组合，充分发挥两种材料的优良特性，具有显著经济效益，已成为结构体系的重要发展方向之一[1]。但同时，由于其由不同材料的构件组成，致使其抗震性能较为复杂，因此，有必要对其进行详尽的抗震性能研究并建立适宜的抗震分析方法。目前，国内外学者已进行了一系列组合构件、组合节点、局部组合框架抗震性能试验研究及数值模拟分析[2−11]，但建立适用于组合框架的抗震分析方法尚需进一步研究和探索。

《建筑抗震设计规范》(GB 50011−2010)提出了三水准设防目标，即“小震不坏、中震可修、大震不倒”，与此相应结构抗震分析分为2部分：除规范特别规定外，建筑结构应进行多遇地震下的内力和变形分析，该部分基于线弹性理论，发展已较为成熟；对不规则且具有薄弱部位的建筑结构应进行弹塑性变形分析，该部分规范建议了2种分析方法，即推覆分析和弹塑性时程分析。其中，弹塑性时程分析计算量大，成本相对较高，需要较好的计算机软件和很好的工程经验；推覆分析实施相对简单，成本较低，是目前较为有效的分析方法，但仍有其局限性并需要工程经验判断[12]。鉴于此，本文应用极限平衡理论，研究钢与混凝土组合框架结构在罕遇地震作用下达到丧失工作能力时，通过外界条件与内在因素的相互关系，寻找各种极值以及结构各部分内力和变形分布规律，建立一种组合框架结构罕遇地震作用时简化分析方法。

1 极限平衡理论概述

根据文献[13]，应用极限平衡理论进行钢-混凝土组合框架结构抗震分析，即依据组合框架在极限状态下内力与变形的分布规律，并结合能量法用以预期组合框架的抗震强度。此处，抗震强度是指结构达到极限状态时所能承担的地震作用。以下为极限平衡理论的2个基本原理和3个基本假定。

基本原理一：极限平衡理论基本规律。结构达到承载能力极限状态时，仅在所形成的塑性域内材料应力达到计算强度，被塑性域分割的各块体于外荷载作用下处于平衡状态，并在满足极限变形的条件下形成一个机动体制。

基本原理二：结构破坏唯一性规律。结构在一定外界条件作用下而丧失工作能力时，在满足极限变形条件下，相应于位能最小的塑性域所形成的图形为结构唯一破坏图形。

第一假定：刚塑体假定。结构达到极限状态时，被塑性域分割的各块体，其变形认为集中在塑性域内，而各个块体视为刚体。

第二假定：应力假定。结构达到极限状态时，在所形成的塑性域内，材料均达到计算强度。

第三假定：变形假定。寻求极限状态下各种极值时，可略去结构变形后几何尺寸的改变。

2 组合框架抗震强度分析

2.1 抗震强度分析过程

在水平地震作用下，达到极限平衡状态时，结构内部产生足够多的塑性铰形成破坏机构，并仍然满足平衡的条件：当结构产生一个可能的无限小的位移时，外力和内力虚功增量的总和应等于0，即可应用能量法计算得到组合框架抗震强度。根据破坏唯一性规律，可以预先决定出结构极限状态时的破坏机构，再依次进行计算。

结构破坏机构可以通过2种方法判别，其一是通过试验确定；其二是通过理论分析得到结构在给定外力分布下的破坏规律。两种方法应相辅相成，找到满足极限平衡第一基本原理(平衡、屈服、机动、变形条件)的真实破坏机构。

汇总分析国内外十九榀组合框架试验，破坏时基本都形成了较为理想的梁铰破坏机制。对如图1所示多层多跨梁侧移破坏机制框架进行抗震强度分析，用施加在框架上的倒三角形水平侧力模拟水平地震作用，将重力荷载简化为施加在框架柱顶的轴向力。

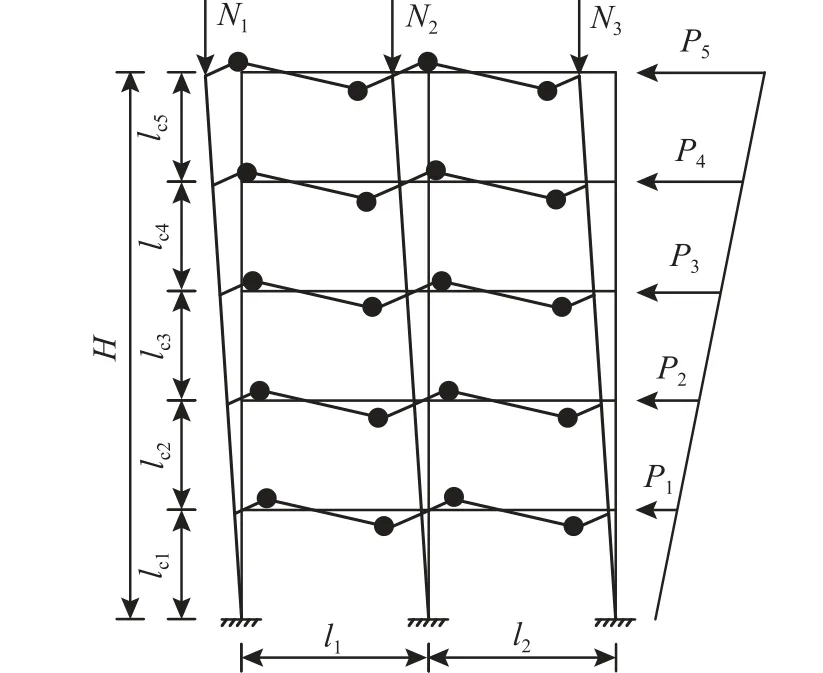
图1 梁侧移型破坏机构Fig. 1 Beam sideway mechanism

该破坏机制仅在梁端与底层柱下端出现塑性铰，极限状态下假定塑性变形集中在塑性铰区域内，忽略弹性变形。以柱底塑性转角表示结构侧向位移：

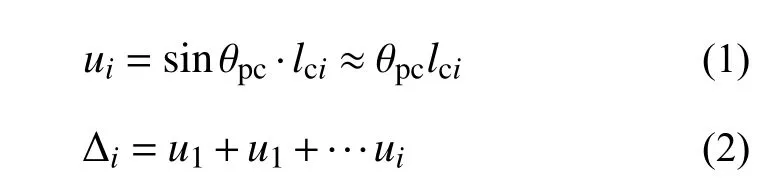
式中：ui为第i层层间侧向位移；Δi为第i层相对于结构底部的侧向位移；θpc为柱底塑性转角；lci为第i层柱计算层高。

图2表示梁与柱的变形几何细节，忽略结构变形对几何尺寸影响。其中，d = ljsinθpc≈ ljθpc≈lbjθpb，从而有：

图2 变形几何关系Fig. 2 Geometric relationship of deformation

式中：θpb为梁端塑性转角；lj和lbj分别为第j跨梁计算跨长和梁中正负弯矩塑性铰之间距离(梁端塑性铰长度可取1倍～1.5倍的梁高)。

同样，忽略柱的伸缩变形而仅产生倾斜，结构竖向位移可用柱底塑性转角表示为：

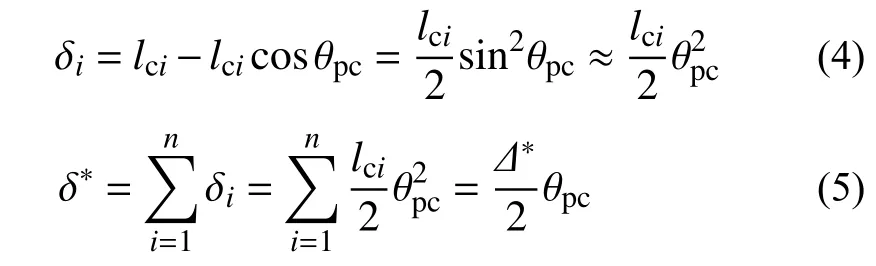
式中：δi为第i层层间竖向位移；δ*和Δ*分别为结构顶部相对与结构底部的竖向位移和侧向位移。

经过以上分析得到结构在给定破坏机制下各变形之间的的几何关系，由虚功原理可得：

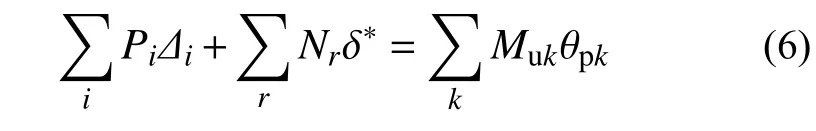
式中：Pi为施加在框架第i层的等效侧力；Nr为施加在第r根柱子上的轴向力；Muk为第k个塑性铰处的极限弯矩。

将式(1)～式(5)带入式(6)中，分别取Δ*等于H/50、H/40、极限荷载对应侧移，通过计算预估框架抗震强度。

2.2 真实破坏机构理论分析

结构达到极限平衡状态时，真实破坏机构唯一并满足平衡、屈服、机动、变形条件，可根据上限定理判断结构真实破坏机构[14]。

假定作用在结构上的外荷载以同样比例因子增长，当增加到给定荷载的s倍时，结构达到极限平衡状态，比例因子s称为极限荷载乘子。

具体可应用机构叠加法确定结构真实破坏机构。通过叠加基本机构以创建复合机构并同时叠加相应的内、外功等式，求出运动许可乘子s¯，逐渐减小运动许可乘子，适时停止计算，选择其中最小运动许可乘子s¯min对应机构，判断其内力场静力容许时，该机构即为结构真实破坏机构。

实际上，组合框架塑性铰发生方式由结构外界条件和结构几何特征、材料性能、节点构造等多种因素共同决定，理论分析结果应与试验方法相互比对。

3 算例及分析

3.1 钢梁-钢筋混凝土柱组合框架抗震强度计算

白国良等[15]1993年进行了一榀1/3比例两跨三层S梁-SC柱组合框架抗震性能试验。试验概况如图3所示，试件截面尺寸及配筋如图4所示，材料力学性能实测值列于表1。

表1 材料力学性能Table 1 Mechanical properties of materials

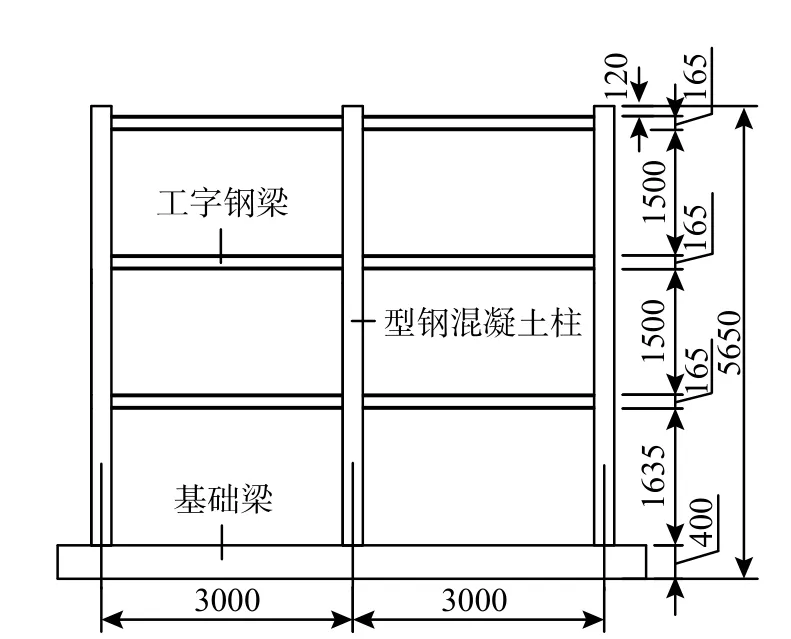
图3 试验试件构造Fig. 3 Details of test specimen

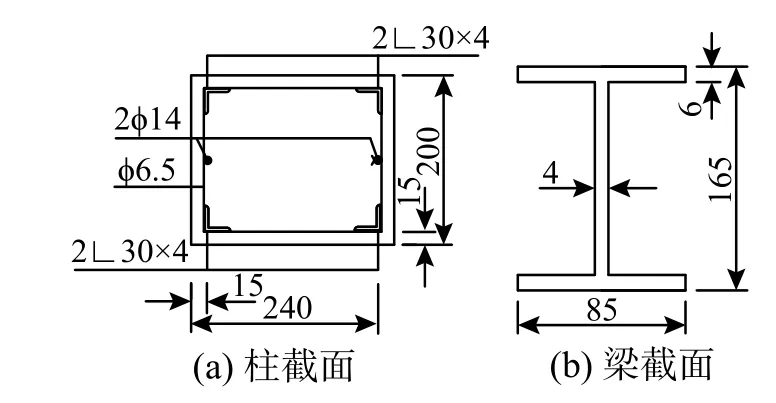
图4 试验尺寸及配筋Fig. 4 Size and reinforcement of specimen

3.1.1 计算构件截面极限弯矩Mu

1) 柱截面极限弯矩Muc

为柱截面极限承载力计算简图如图5所示，计算值时将纵向受力型钢简化为等面积钢筋放置在角钢形心处。受压区边缘混凝土应变达到0.004时，根据应变分布和平衡条件计算截面极限弯矩[16]，计算时材料强度取试验实测值。

图5 柱截面受力简图Fig. 5 Force diagram of column section

若εsi＞εsyi，则取εsi=εsyi，

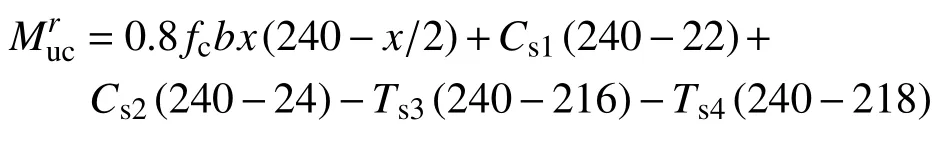
施加在框架柱上的轴力N=330 kN，x=79 mm，Muc=6.932×107N∙mm 。

2) 梁截面极限弯矩Mub

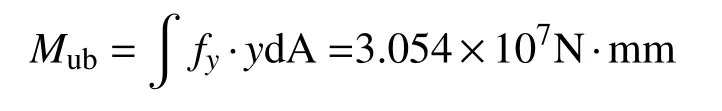
3.1.2 结构真实破坏机构判别

在框架上施加倒三角形外力分布，结构计算简图如图6所示，其中M0=1.0×107N∙mm，L0=1000 mm，P0=M0/L0，图中虚线侧受拉弯矩记为正。结构共有3个侧移基本机构和7个节点转动基本机构。通过叠加基本机构及相应的功能等式，得到最小运动许可乘子smin=2.438，对应的破坏机构如图7(a)所示。通过绘制弯矩图判断其内力分布为静力容许，即该机构为结构计算真实破坏机构，试验中得到的结构破坏机构如图7(b)、图7(c)所示，同样形成了理想的梁铰破坏机制。

图6 结构计算简图Fig. 6 Structural calculation diagram

3.1.3 组合框架抗震强度计算及对比分析

依据组合框架真实破坏机构(图7(a))，用虚功等式(6)计算抗震强度并与试验实测承载力进行对比，列入表2中。由表2可得：当框架顶部侧移达到H/50、H/40时计算值与试验值吻合很好(0.51%、−2.10%)，取框架顶部侧移等于极限荷载对应侧移时计算得到框架抗震强度略大于试验值(7.40%)，可能由于计算时未考虑往复加载后期结构损伤产生的影响；同时计算中也忽略了钢材强化及其他可能影响框架抗震强度因素，但从计算结果可看出，简化分析得到的抗震强度与试验值差距不大(±10%以内)。

表2 计算结果及对比Table 2 Calculation results and comparison

同时观察试验得到的滞回曲线，如图8所示。滞回环饱满无捏缩，整体呈现理想的梭形，弹塑性变形后期承载力下降较为平缓，说明该简化分析用于钢梁-型钢混凝土柱组合结构，可以便捷有效的得到一个较为保守的抗震强度。

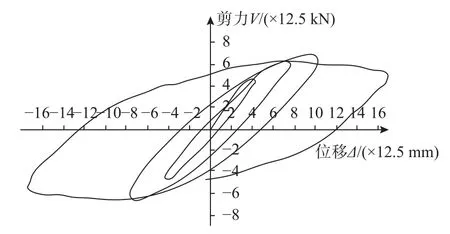
图8 顶层层间剪力-位移滞回曲线Fig. 8 Story shear-drift hysteresis loops of RF

3.2 试验汇总及对比

基于极限平衡对组合框架进行简化分析，讨论范围为以第一振型为主的单、多层组合框架，并期望框架达到理想的梁侧移机制。为了更好地说明该简化分析方法的有效性，收集了国内外十九榀单、多层钢与混凝土组合框架低周反复荷载试验[15,17−22]，分别取柱顶侧移等于H/50、H/40、极限荷载对应侧移计算抗震强度并与试验结果对比。考虑到不同试验对试件极限状态定义不同对结果对比带来影响，此处，极限状态统一定义为荷载下降至峰值荷载的85%时，对应的荷载取为极限荷载，若试验中荷载未下降至峰值荷载的85%，则取破坏时荷载为极限荷载，试验值与计算值的统计及比值列于表3。当框架层间位移角限值为1/50时，极限强度试验值与计算值比值的平均值为1.0058、方差为0.0054、标准差为0.0735、变异系数为0.0731，二者吻合较好；当弹塑性层间位移角限值为1/40时得相近数值。同时，以上十九榀组合框架试验得到的滞回曲线大多呈现较为饱满的滞回环，说明组合框架结构具有良好的变形和耗能能力。钢与混凝土组合结构框架可应用本文简化分析方法预期抗震强度，并可以放宽其位移角限值为1/40。

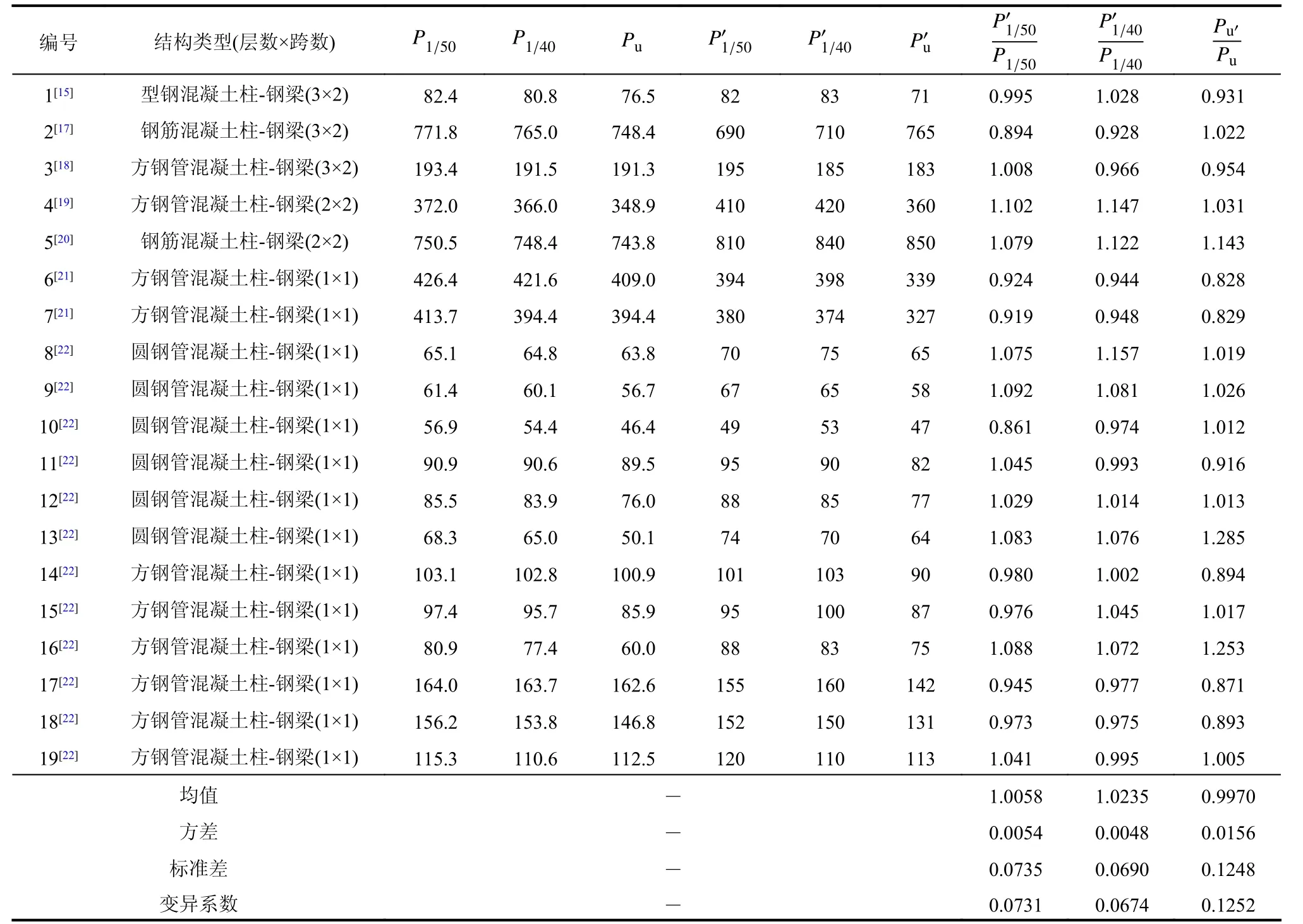
表3 计算结果及对比Table 3 Calculation results and comparison

4 “大震不倒”控制方法

4.1 简化控制方法

将多质点结构体系视为等质量、等周期的单质点体系，假定其完全弹性时，分别计算罕遇地震作用和多遇地震作用(基底剪力)，记作Ve1和Ve2；考虑其弹塑性反应时，以多遇地震作用控制框架屈服，框架达到极限变形时地震作用记作Vu′′(基底剪力)；根据能量相等的概念，即最大变位时弹性体系储存的位能与最大变位时弹塑性体系储存位能相等，假定结构弹性和弹塑性的反应如图9所示。

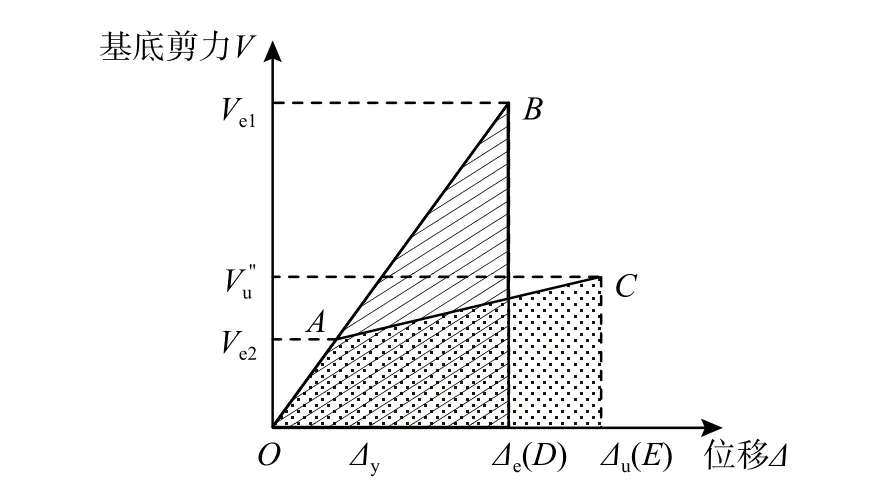
图9 结构地震反应Fig. 9 Seismic response of structures

将Ve2与Ve1的比值记作系数R1，将与Ve1的比值记作系数R2，Δu与Δy的比值为结构位移延性µ，根据位能相等，即图中面积OBD等于面积OACE，可建立R1、R2、µ之间的关系等式：

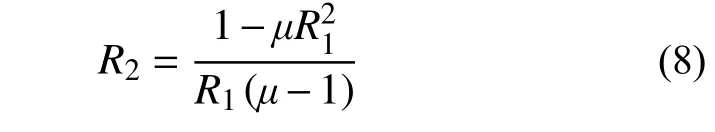
按照《建筑抗震设计规范》(GB 50011−2010)，参考混凝土框架及多高层钢结构取组合结构位移角限值取结构位移角限值1/50，此时可通过式(19)计算相应弹塑性地震作用(基底剪力)；基于极限平衡计算框架抗震强度(基底剪力)并通过抗震调整系数γRE对结构抗震强度进行调整；调整后的抗震强度与地震作用对比，两者关系如图10所示。

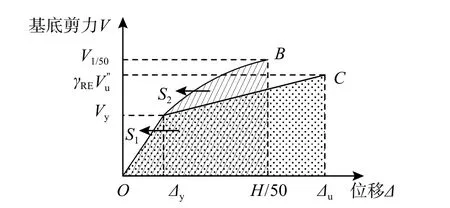
图10 结构能量关系Fig. 10 Relationship of structural energy

当组合框架位移角达到1/50时，即梁侧移破坏机制框架的顶部侧移为H/50，此时若结构实际位能S2大于地震输入能量S1，则结构满足抗震安全。为方便抗震验算取地震作用与计算抗震强度V1/50进行比较，即为保证罕遇地震抗震安全，需满足如下等式：

4.2 算例及分析

假定设防烈度8度(0.2 g)，设防分组第二组，场地类别II类，以前述两跨三层S梁-SC柱框架[15]为例，详细分析说明罕遇地震抗震强度验算步骤。试验实测框架位移延性为4.95，计算多遇地震作用时阻尼比取0.05，计算罕遇地震作用时阻尼比取0.185[23]。

第一步：底部剪力法计算弹性地震作用

Geq=0.85ΣNr=841.50 kN

T=0.025H=0.126 s

多遇地震作用：

αmax=0.16，Tg=0.40 s

0.1＜T1＜Tg，α=αmax=0.16

底部剪力：FEK=αGeq=134.64 kN

即，Ve2=134.64 kN

罕遇地震作用：

αmax=0.9；Tg=0.45 s

0.1＜T1＜Tg，η2=0.6，α=η2αmax=0.54

底部剪力：FEK=αGeq=454.41 kN

即，Ve1=454.41 kN

第二步：弹塑性地震作用计算

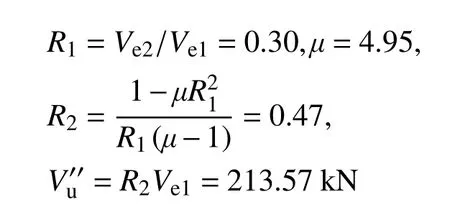
第三步：抗震强度对比验算

基于极限平衡理论，可计算得到组合框架抗震强度(Δ=H/50)，抗震调整系数取0.75，调整结构计算抗震强度并与地震作用对比。

结构抗震强：V1/50=164.84 kN

V1/50/γRE=219.79 kN

V′′u

V1/50/γRE＞

该榀组合框架抗震强度满足8度设防时罕遇地震抗震强度要求。

4.3 试验汇总分析

取结构位移角限值1/50、1/40，阻尼比取为0.185，计算前面汇总试验中前五榀多层多跨组合框架的地震作用，并与基于极限平衡计算得到的抗震强(Δ=H/50、Δ=H/40)进行对比，评估各榀框架罕遇地震抗震情况，计算结果及对比见表4。编号µV′′u/kNV1/50/γRE/kNV1/40/γRE/kN 1[15]4.95213.57219.78215.38 2[17]8.00376.652058.012040.08 3[18]4.43388.56515.65510.61 4[19]6.10569.21744.08732.08 5[20]5.42272.141501.461497.16

五榀框架均可满足8度设防时罕遇地震抗震强度要求，其中框架2延性很好(µ=8)，观察其试验滞回曲线，发现即使到了塑性变形阶段后期(θ＞1/25)承载力仍无下降趋势，实际强度远远满足要求。

通过前面基于极限平衡的抗震强度简化分析，同时观察试验滞回曲线可看出框架位移角达到1/50后承载力并没有发生急剧下降，最终极限位移角达到了1/39～1/25，建议组合框架位移角限值为1/40，并可采上述步骤进行罕遇地震抗震验算，评估组合框架罕遇地震抗震情况，进行设计调整，以达到“大震不倒”设防目标。