循环荷载作用下粉砂岩疲劳流变损伤模型研究

2022-07-04苗胜军杨鹏锦梁明纯王亚欣

工程力学 2022年7期

苗胜军，杨鹏锦，王辉，梁明纯，王亚欣

(1. 北京科技大学城市地下空间工程北京市重点实验室，北京 100083；2. 北京科技大学土木工程系，北京 100083)

岩体工程在施工及运营阶段经常会受到循环荷载作用，如地下硐室的爆破开挖与支护、水库周期性蓄水和放水、岩盐储气库的注气和采气过程等[1]。定量化研究循环荷载作用下岩石的疲劳损伤特性及其变形演化规律，对岩体工程长期稳定性评价具有重要的理论指导意义。

国内外学者对岩石的疲劳变形特性开展了大量的研究。Bagde等[2−3]通过疲劳试验，发现砂岩疲劳强度随着频率和应力幅值的增加而趋于减小；Jindřich等[4]定性地研究了不同幅值、不同频率循环荷载下砂岩的流变特性，发现平均应力和幅值对岩石变形特征的影响比频率更为显著；Rashid等[5−6]对比分析了花岗岩和砂岩的疲劳破坏机制。杨永杰等[7]认为单轴循环荷载下煤岩体的疲劳强度“门槛值”不超过其单轴抗压强度的81%；葛修润等[8]和章清叙等[9]发现岩石循环加卸载过程中轴向不可逆变形可划分为初始变形、等速变形和加速变形3个阶段；郭印同等[10]通过盐岩疲劳试验研究发现，改变上限应力和平均应力会显著影响疲劳破坏的进程；卢高明等[11]发现围压对轴向变形有一定强化作用，且变形比强度更适合作为岩石疲劳破坏的依据。

循环荷载作用下，岩石变形破坏表现出显著的时间效应，黄明等[12]基于岩石流变特性建立了广义Kelvin-Voigt体的正弦加载蠕变模型；许宏发等[13]将损伤变量引入累积塑性应变中，推导了高周期和低周期循环荷载作用下岩石轴向塑性应变方程；王军保等[14]基于低频循环荷载蠕变试验，推导了循环荷载下Burgers模型的轴向蠕变方程；郭建强等[15]将疲劳简化为恒定等效应力下的蠕变过程，建立了岩石的疲劳本构模型；李永辉等[16]将西原模型中线性黏性元件替换为含疲劳参数的非线性黏性元件，建立了循环荷载下改进的西原疲劳模型；刘斌等[17]基于应力耗散原理建立了非线性黏壶力学元件，推导获得循环荷载下应变随时间变化的本构方程。

综上，将循环荷载简化为恒定应力来建立流变本构模型的方法虽然可以较好地拟合试验结果，但不够严谨，物理意义模糊；此外，当前鲜有将损伤变量引入流变模型描述循环荷载下岩石疲劳破坏加速流变阶段的研究。

因此，本文根据正弦波循环荷载作用下粉砂岩疲劳变形破坏试验结果，在Burgers模型的基础上引入黏塑性损伤元件构建岩石疲劳流变损伤模型，并以正弦波循环荷载为例，将应力-时间函数替换流变微分本构方程中的恒定应力，推导循环荷载作用下岩石一维、三维非线性流变损伤方程。最后，验证了模型的合理性和适用性，分析了不同上限荷载下流变本构模型参数的演化规律，并讨论了岩石疲劳寿命的预测方法。

1 粉砂岩疲劳试验及结果分析

1.1 正弦波循环荷载下粉砂岩疲劳试验

本次试验所选取的粉砂岩主要矿物成分为石英、斜长石、云母类和整柱石。如图1所示，按照国际岩石力学试验标准将岩样加工成ϕ50 mm×100 mm的圆柱体，试样上、下端面的不平整度控制在 ±0.02 mm以内，并根据超声波速测试剔除了离散性较大的试样。

图1 岩石试样Fig. 1 Rock samples

本次试验采用的MTS815岩石液压伺服力学系统可施加频率为0.01 Hz～5 Hz的轴向正弦波、三角波、矩形波、斜波、随机波和组合波荷载。通常，正弦波形式的循环荷载更接近岩体工程受到的动力扰动模式，因此，本次试验对试件施加正弦波循环荷载。

应力路径如图2所示。图中σ(t)为时间t时的应力值；σmin为循环荷载下限应力，σmax为循环荷载上限应力；平均应力a=(σmax+σmin)/2，应力幅值b=(σmax−σmin)/2 ；T为循环周期。

图2 应力路径Fig. 2 Path of stress loading and unloading

因此，正弦波应力函数可表示为：

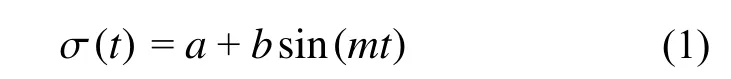
式中，m=2π/T。

为选择合适的循环荷载上限，首先开展了5组单轴压缩试验，粉砂岩的单轴抗压强度和弹性模量均值分别为34.76 MPa和5.03 GPa。根据粉砂岩单轴压缩强度特征，循环荷载上限设定为30 kN、40 kN、45 kN、55 kN、60.5 kN、61 kN、61.5 kN、63 kN、65 kN，循环荷载下限为5 kN，循环频率为0.5 Hz，试验方案及结果见表1。

表1 试验方案及结果Table 1 The scheme and results of test

1.2 不同循环荷载上限下粉砂岩疲劳变形特性

不同循环荷载下粉砂岩应力-应变曲线(以上限荷载30 kN、45 kN、61 kN为例)如图3所示，由表1和图3可知：上限荷载为55 kN时，循环加卸载15 000次后试样仍未发生疲劳破坏，由此可初步推断正弦波循环荷载作用下粉砂岩的疲劳强度在28.06 MPa～30.88 MPa(55 kN～60.5 kN)，约为单轴压缩强度的80%～90%。当上限荷载高于60.5 kN时，试件发生疲劳破坏，且破坏时的轴向变形量与单轴压缩应力-应变全过程曲线峰后区在循环载荷上限位置的变形量相当。

图3 不同上限荷载下粉砂岩轴向应力-应变曲线Fig. 3 Axial stress-strain curves of siltstone under different upper limits of cyclic loading

图4为不同上限荷载下粉砂岩平均应变(上限应变与下限应变的平均值)随时间演化曲线。可以看出，当上限荷载低于疲劳强度时，粉砂岩轴向应变-时间曲线均表现为初始变形、匀速变形2阶段；循环荷载上限高于疲劳强度时，轴向应变-时间曲线呈典型的初始变形、匀速变形和加速变形3阶段演化特征。

图4 粉砂岩平均应变随时间演化曲线Fig. 4 Time evolution curves of average strain of siltstone

分析认为，岩石是一种含有天然裂隙、孔隙的非均质材料，试验初始阶段，岩石内部晶格缺陷、微裂纹、软弱界面在循环荷载作用下不断闭合，应变量显著增加；多次循环后，岩石原生缺陷逐渐压密，变形进入匀速阶段，应变量表现为随时间缓慢匀速增加；当循环荷载上限超过疲劳强度，岩石应变量到达某一值时，内部微裂纹不断的扩展贯通，变形进入加速阶段，岩石损伤发育表现显著并发生疲劳破坏；而当循环荷载上限低于疲劳强度时，循环往复的加卸载作用无法使岩石内部微裂纹进一步大量萌生扩展，疲劳寿命表现为无穷大。

2 循环荷载下岩石疲劳流变损伤模型

根据粉砂岩的疲劳变形规律，构建岩石疲劳流变损伤模型，与试验相对应，采用正弦波应力函数替换流变微分本构方程中的恒定应力，并推导模型一维和三维非线性流变损伤方程，具体过程如下。

2.1 循环荷载下Burgers流变模型

2.1.1 循环荷载下Maxwell体流变方程

Maxwell体由一个虎克体和一个牛顿体串联组成，其流变微分本构方程为：

式中：σM、EM和ηM分别为Maxwell体的应力、弹性模量和黏性系数；ε˙M和σ˙M为Maxwell体的应变和应力对时间t的一阶导数。

正弦波循环荷载下Maxwell体的流变微分本构方程可转变为：

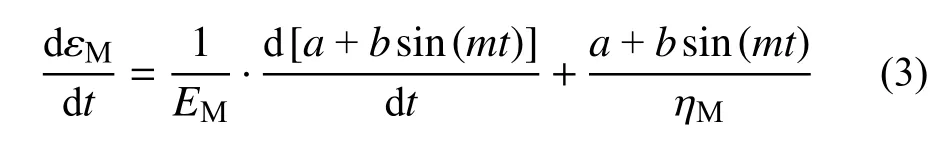
对式(3)两端进行积分，可以得到正弦波循环荷载作用下Maxwell体的流变方程：

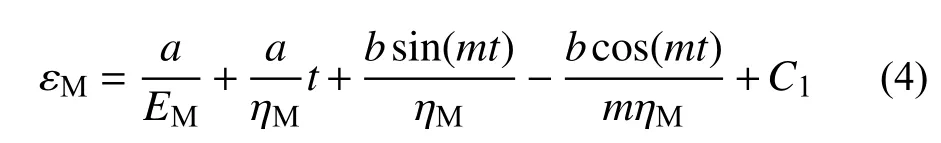
式中，C1为积分常数。当t=0时，εM=0，则：

将式(5)代入式(4)，可得：

2.1.2 循环荷载下Kelvin体流变方程

Kelvin体由一个虎克体和一个牛顿体并联组成，其流变微分本构方程为：

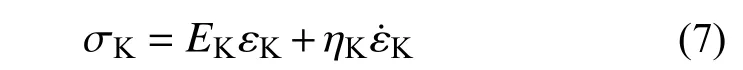
式中：εK、σK、EK和ηK分别为Kelvin体的应变、应力、弹性模量和黏性系数；ε˙K为Kelvin体的应变对时间t的一阶导数。

正弦波循环荷载下Kelvin体的流变微分本构方程可转变为：

解式(8)的一阶线性微分方程，可得正弦波循环荷载作用下Kelvin体的流变方程：

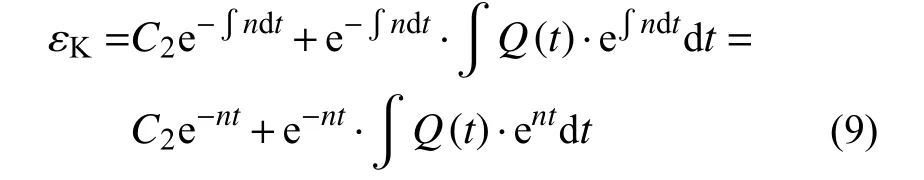
式中，C2为积分常数，其中：

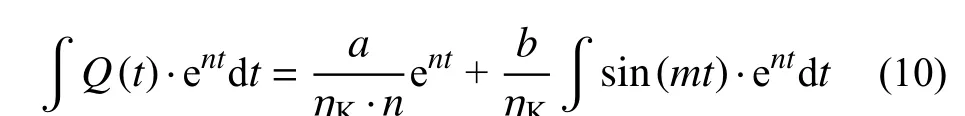
对式(10)中的∫sin(mt)·entdt进行二次分部积分，则：

进一步整理化简，可得：

研究区属于寒温带湿润季风气候。其特点是冬长夏短，春秋相连，低温湿润，日照少。冬季长达9个月（平均气温<10℃），最低气温为-58℃，最高气温达到40℃，降水集中在7、8月份，年降水量在450～550 mm，冻结期在7个月以上；9月底至第2年的5月初为降雪期，降雪厚度一般在20～40 cm；年均日照为2 594 h，无霜期90 d左右。

将式(10)、式(12)代入式(9)，得：

当t=0时，εK=0，则：

将式(14)代入式(13)，可得：

2.2 循环荷载下非线性黏塑性损伤元件

为了准确地描述循环荷载下岩石的疲劳破坏规律，如图5所示，引入一个非线性黏塑性损伤元件来描述循环荷载作用下岩石加速流变阶段。

图5中，σS为岩石疲劳强度；εa为应变阈值，用于判断岩石进入加速流变阶段的应变状态；ηVP和D分别为非线性黏性损伤元件的黏性系数和损伤变量。当循环荷载上限应力σmax≤σS时，非线性黏塑性损伤元件不起作用，岩石不会发生加速流变；当循环荷载上限应力σmax>σS且ε>εa时，黏性损伤元件启动，岩石进入加速流变阶段。

图5 非线性黏塑性损伤元件Fig. 5 Nonlinear viscoplastic model for damage

基于Lemaitre应变等效假设[18]，将损伤变量引入牛顿体，则非线性黏性损伤元件流变微分本构关系为：

式中，ε˙VP为非线性黏性损伤元件应变εVP对时间t的一阶导数。根据Kachanov[19]流变损伤理论，岩石的流变损伤变量随时间的推移呈负指数函数增长，因此本文引入考虑时间效应的损伤变量：

式中，α为岩石损伤指数。则式(16)可转化为：

对式(18)进行积分，可得正弦波循环荷载下非线性黏塑性损伤元件的流变方程：

式中，C3为积分常数。当t=0时，εVP=0，则：

将式(20)代入式(19)，可得：

2.3 岩石疲劳流变损伤模型一维流变方程

根据以上分析，如图6所示，在Burgers模型的基础上串联非线性黏塑性损伤元件，构建正弦波循环荷载作用下岩石非线性流变损伤模型。

图6 疲劳流变损伤模型Fig. 6 Fatigue rheological damage model

根据模型串并联关系可以得到岩石流变模型的一维流变微分本构方程：

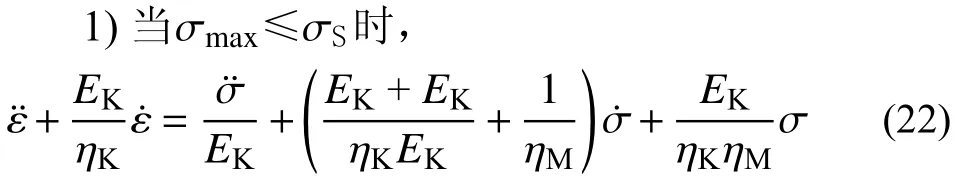
2)当σmax>σS且ε>εa时，

根据叠加原理可以得到正弦波循环荷载作用下岩石的一维流变损伤方程：

1)当σmax≤σS时，

2)当σmax>σS且ε>εa时，

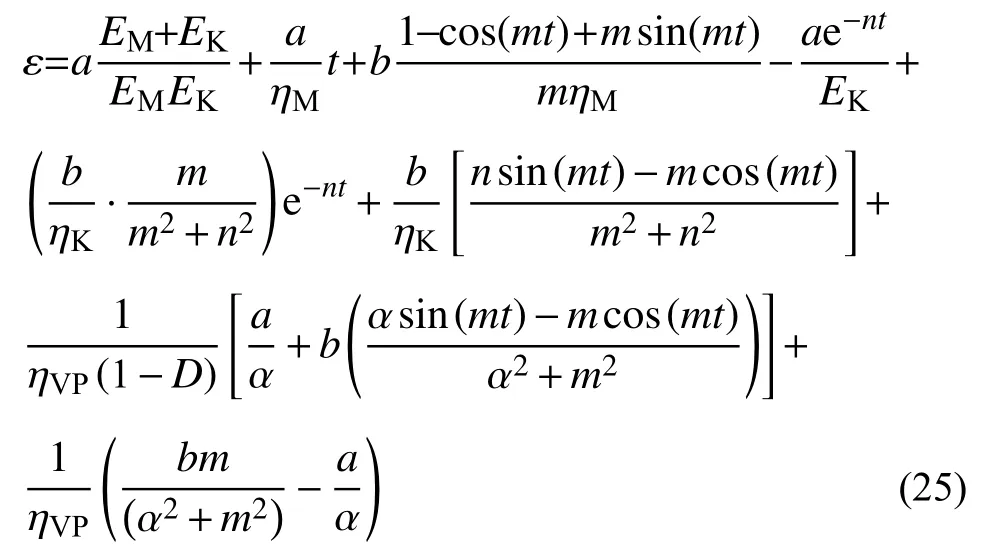
2.4 岩石疲劳流变损伤模型三维流变方程

三维应力状态下，应力张量σij通常基于弹塑性理论分解为偏应力张量和球应力张量，流变方程则可通过类比法由一维流变模型导出。疲劳损伤流变模型的总应变为：

式中：Sij为偏应力张量；δij为Kronecker张量；K1为体积模量；σm为平均应力；N=G2/H2；G1、G2为三维剪切模量；H1、H2、H3为三维黏滞系数。

循环加卸载条件下轴向偏应力和平均应力可表示为：

式中，a1=a−σ3，a2=a+2σ3。

根据一维流变本构方程的积分求解方法，可推导获得三维应力状态下轴向疲劳流变损伤方程：

3 岩石流变损伤模型验证及参数分析

3.1 非线性流变损伤模型适用性验证

由式(25)和式(29)可知，一维状态下模型共有EM、EK、ηM、ηK、α、ηVP和εa这7个参数；三维状态下模型共有K1、G1、G2、H1、H2、H3、α和εa这8个参数。通过Origin软件里的非线性拟合功能Fitting Function Organizer，编写流变方程拟合程序，然后采用Analysis-Fitting-Nonlinear Curve Fit进行数据拟合，为了避免因参数过多和初值选取不当造成拟合不收敛或陷入局部最优，采用Levenberg - Marquardt法进行迭代计算模型各参数的理论值，然后代入流变损伤方程可获得循环荷载作用下岩石流变损伤的理论曲线。

试验采用的粉砂岩的疲劳强度值在28.06 MPa和30.88 MPa之间，因此，取二者平均值29.47 MPa作为本次一维流变模型拟合的疲劳强度值σS。以上限荷载45 kN和61 kN为例，粉砂岩试验结果与理论曲线对比如图7所示，一维非线性流变损伤模型参数见表2。为了验证三维状态下流变损伤模型的适用性，选用文献[11]中与本次试验粉砂岩力学性质相近的黄砂岩试验数据进行拟合。文献[11]开展了围压为5 MPa、10 MPa、20 MPa的黄砂岩轴向循环加卸载试验，试验结果和理论曲线对比与模型参数分布如图8和表3所示。结果表明，一维和三维状态下理论曲线与试验结果的吻合度较好，说明本文建立的流变损伤模型不仅可以精确反映岩石的衰减流变和稳态流变，还可以准确地描述上限荷载高于疲劳强度时的加速流变，具有较好的适用性。

表3 三维流变模型参数拟合结果Table 3 Parameters of three dimensional rheological model

图7 粉砂岩理论曲线与实验结果Fig. 7 Comparison between theoretical curve and test results of siltstone

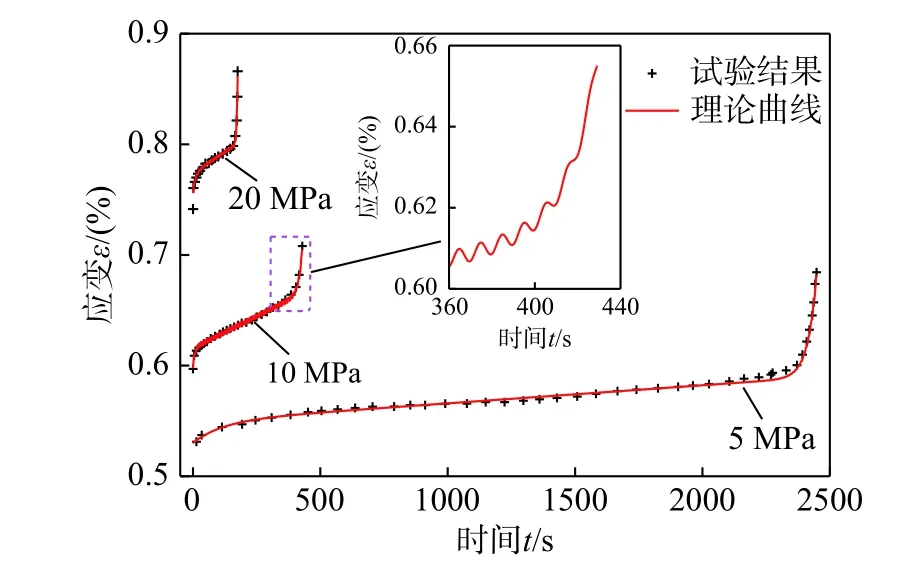
图8 围压5 MPa、10 MPa、20 MPa时理论曲线与实验结果Fig. 8 Comparison between theoretical curves and test results at confining pressure of 5 MPa、10 MPa、20 MPa

表2 一维流变模型参数拟合结果Table 2 Parameters of one dimensional rheological model

3.2 岩石疲劳损伤流变全过程定量化分析

3.2.1 上限荷载对衰减流变阶段的影响

Kelvin体是由虎克体和牛顿体并联形成，牛顿体推迟了虎克体的弹性变形，流变特征表现为衰减流变。因此选取弛豫时间τ表示Kelvin体弹性变形的推迟时间，根据模型性质可将τ定义为：

将式(30)代入Kelvin体流变方程中可知，当t=τ时：

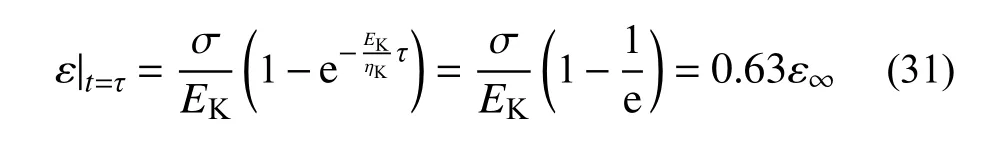
式中，ε∞为流变达到稳定状态的最终变形，推迟时间为衰减流变达到稳定变形所经过时间的63%。Kelvin体系数n 和弛豫时间τ互为倒数，n越大，τ越短，稳定流变阶段历时越短；n越小，τ越长，由衰减流变过渡到稳态流变阶段所需的时间越长。

从图9不同上限荷载下粉砂岩Kelvin体系数n 和弛豫时间τ的演化曲线可以看出，Kelvin体系数n 和弛豫时间τ随着上限荷载的增加分别呈非线性指数型增加和减少，说明循环荷载对粉砂岩原生裂隙和孔隙的压密作用显著，且上限荷载越大，对粉砂岩压密作用的时效性越显著。

图9 Kelvin体系数n 和弛豫时间τ的演化曲线Fig. 9 Evolution curves of nand τ under different upper limit of cyclic loading

3.2.2 上限荷载对稳态流变阶段的影响

循环荷载作用下，岩石内部原生缺陷压密和微裂纹萌生扩展两种效应即相互对立，又同时存在，是一个交互作用的过程[21]。岩石的稳态流变速率可根据循环荷载平均应力a和Maxwell体黏性系数ηM的比值计算获得。如图10所示，稳态流变速率随着上限荷载的增加呈非线性指数型增大。上限荷载较低时，岩石内部微结构以压密为主，稳态流变阶段微裂纹扩展速度缓慢；当上限荷载大于疲劳强度时，微裂纹萌生、扩展占据主导地位，岩石发生加速流变破坏，稳态流变速率显著增加，约为上限荷载低于疲劳强度时的20倍～1300倍。

图10 稳态流变速率的演化曲线Fig. 10 Evolution curves of steady state rheological rate under different upper limit of cyclic loading

3.2.3 加速流变阶段损伤演化规律

图11为不同黏性系数ηVP和损伤指数α条件下的黏塑性损伤元件流变曲线，由图11可知，随着ηVP值的减小，单位时间段内流变变形量增加，岩石的流变能力增强；与ηVP值不同，损伤指数α值越大，损伤发育越迅速，流变速率越大，加速流变曲线的非线性特征越明显，说明损伤指数α值对加速流变阶段的持续时间和流变曲线特征有明显的控制作用。

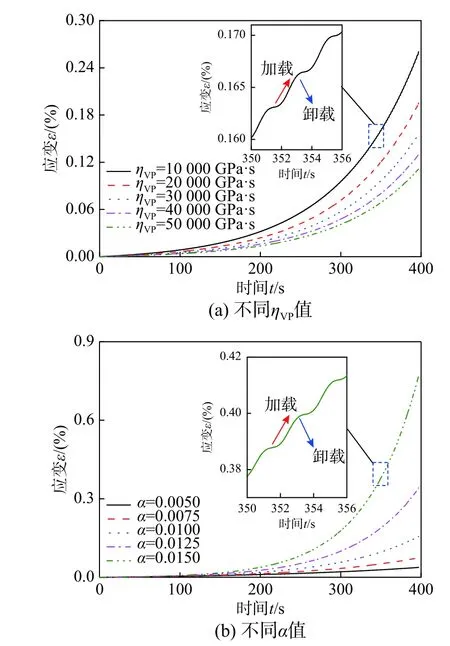
图11 ηVP和α对非线性黏塑性损伤元件流变曲线的影响Fig. 11 The effect of ηVP and α on rheological curves of nonlinear viscoplastic model

疲劳破坏阶段岩石内部裂纹不断扩展、交汇、贯通，损伤不断累积，岩石塑性特征明显。从图11可以看出，循环荷载作用下岩石的流变曲线随时间推移呈台阶状增加，加载过程中，流变曲线的变形量显著增加，卸载过程中，流变曲线增长较为平缓，循环荷载作用下岩石变形具有显著的不可逆性[22]。由此可见，本文建立的黏塑性损伤元件不仅在整体变形规律方面与岩石疲劳破坏的加速流变特征相吻合，而且能很好地体现循环荷载作用下岩石不可逆黏塑性变形特征和损伤发育规律，具有明确的物理意义。

4 讨论

本文通过建立循环荷载作用下岩石疲劳流变损伤模型，定量研究了不同上限荷载下粉砂岩的变形及损伤特性。在此基础上，本节通过建立临界损伤阈值判据和加速流变失稳破坏判据，开展岩石疲劳寿命预测分析，进一步明确本文所建立的循环荷载作用下岩石流变模型对岩体工程长期稳定性评价的意义。

4.1 加速流变损伤阈值及失稳判别准则

4.1.1 临界损伤阈值判据

在岩石流变破坏过程中，发生加速流变时存在一个临界损伤阈值，可以用裂纹临界密度指标法、加速流变临界应变法、全过程应力-应变曲线法、非弹性体积应变法等[23]方法判断加速流变启始的临界条件。对于岩石疲劳变形及破坏特性，Brown和Hudson[24]、葛修润[8]等发现岩石疲劳破坏时的轴向变形量与静态应力-应变全过程曲线峰后区在循环载荷上限位置的变形量相当。如图12所示，粉砂岩轴向平均应变的加速流变启始点对应的应变阈值εa与循环荷载上限呈现良好的线性关系。因此，本文选择疲劳流变损伤模型中黏塑性损伤元件应变阈值εa作为临界损伤阈值判据。

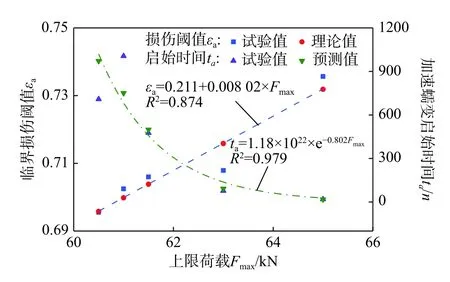
图12 临界损伤阈值和加速流变启始时间Fig. 12 Damage threshold and start time of accelerated creep

根据损伤阈值εa试验值的拟合结果，给出循环荷载下粉砂岩加速流变启始点的临界损伤阈值判据：

通过临界损伤阈值判据获取不同上限应力条件下损伤阈值εa的理论值，代入流变损伤式(25)可计算加速流变启始时间ta的预测值。

4.1.2 加速流变失稳破坏判据

进入加速流变阶段，流变模型中的黏塑性损伤元件启动，轴向应变表现出显著的不可逆性特征，流变曲线快速增长，损伤不断累积。根据文中流变模型引入的损伤变量式(17)，当损伤变量D达到1时岩石发生加速流变失稳破坏，则可得加速流变失稳破坏判据为：

式中，tF为加速流变持续时间。

如图13所示，对试验结果进行拟合并获取不同上限荷载条件下损伤指数α理论值，可通过加速流变失稳破坏判据式(33)计算获取加速流变失稳破坏时间的预测值。

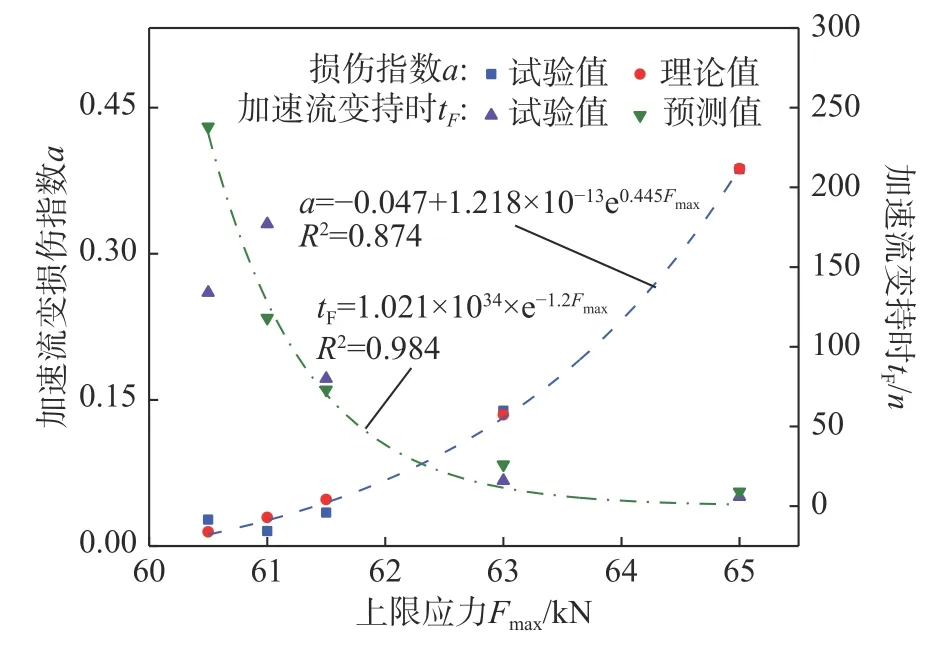
图13 损伤指数和加速流变持续时间Fig. 13 Damage index and accelerated creep duration

4.2 岩石疲劳寿命预测

根据加速流变损伤阈值判据式(32)和加速流变失稳破坏判据式(33)可分别计算出进入加速流变阶段所需循环时间和加速流变持续时间，因此可通过式(34)计算循环荷载作用下岩石的疲劳寿命预测值：

如图14所示，上限荷载为60.5 kN、61 kN、61.5 kN、63和65 kN时，疲劳寿命预测值分别为1210次、869次、572次、118次和27次，疲劳寿命预测值与试验值吻合度较高，并与上限荷载呈现良好的指数函数关系，说明采用本文建立的流变损伤模型对于定量研究循环荷载作用下岩石的疲劳特性及岩体工程长期稳定性评价具有一定的理论指导意义。