配电系统双时间尺度电压管理的深度强化学习方法

冯昌森，张 瑜，谢路耀，文福拴，张凯怡，张有兵

（1. 浙江工业大学信息工程学院，浙江省杭州市 310023；2. 浙江大学电气工程学院，浙江省杭州市 310027）

0 引言

分布式可再生能源发电在配电系统中的渗透率不断提高，其出力的波动性与不确定性导致系统电压频繁越限［1］。为保证配电系统安全可靠运行，亟需合理的电压管理方法，有效协调具有不同响应特性的调压设备，从而在多时间尺度上挖掘多种设备联合控制电压的潜力，进而抑制可再生能源发电对配电系统电压的影响。

目前，国内外相关学者针对可再生能源高渗透率的配电网电压管理问题进行了广泛研究。其中，基于局部测量信息的下垂控制方法较早应用到分布式电源有功功率和无功功率控制方面，以平抑电压波动［2］，其相应技术规范已写入IEEE 1547—2018标准［3］。然而，这种局部调压方法无法协调多种调压设备，较难达到全局电压偏差最小的目标。因此，基于最优潮流（optimal power flow，OPF）模型的电压协调控制得到了广泛研究。其中，基于OPF 的电压管理方法可分为2 种。1）单时间尺度模型：主要研究短时间尺度（分钟级）分布式电源逆变器等电力电子调压设备的协调控制。文献［4-5］研究了光伏逆变器和静止无功补偿器在分钟级尺度上的协调控制以达到全网节点电压偏差最小的目标。为实现线上实时控制策略，部分研究学者利用梯度映射法［6］、对偶上升法［7］和广义快速对偶上升法［8］等设计了电压反馈控制模型，从而实现基于局部测量信息的全局优化。部分学者进一步研究了该类反馈控制模型的异步迭代机制［9］，以及通信带宽［10］对电压控制的影响。2）双时间尺度模型：为有效协调配电系统中不同时间尺度响应特性的调压设备，提出了双时间尺度的电压模型。文献［11］利用动态规划法与二阶锥规划算法分别求解日前与日内控制策略。文献［12］利用模型预测控制对两阶段电压管理进行建模，并采用分布式算法进行求解。

以上基于优化模型的两类电压管理模型存在以下2 个问题。1）潮流方程的凸化问题。在优化问题中一般可通过二阶锥松弛［13-14］、半正定松弛潮流模型［15］、忽略网损的线性化配电网潮流模型［16］或电压灵敏度方法［17］对在运行点附近的潮流方程进行线性化。以上方法均不可避免带来计算误差。2）随机变量的建模。无论是基于区间数建模进而转化为鲁棒优化问题［18］，还是采取场景法进而转化为随机优化模型［19］或忽略随机变量的方法均不可避免地带来较高的计算复杂度或较大的误差。为解决以上2 个问题，本文拟利用深度强化学习方法来求解电压管理的决策问题，通过大量样本的线下计算来达到实时控制的效果。

深度强化学习利用奖励函数对决策行为进行评价，能够根据不同的运行要求和优化目标给出最优动作策略，实现实时决策［20］。已有研究将双深度Q网络（double deep Q network，DDQN）算法［21］、对抗Q 算法［22］、rainbow 算法［23］分别应用于配电系统的电压管理、需求响应管理和能量调度方面，以解决离散变量优化问题。文献［24］采用深度确定性策略梯度（deep deterministic policy gradient，DDPG）算法求解包含高维连续优化变量的能量管理问题，回避了对连续变量离散化所导致的误差。文献［25］针对多个光伏逆变器协调控制问题，采用多智能体深度确定性策略梯度（multi-agent DDPG，MADDPG）算法求解，解决了多种调节设备之间的信息交互问题，有效实现了智能体之间的协调控制。

在上述背景下，本文针对调压设备不同时间响应特性和动作特性，建立双时间尺度电压管理模型。通过有效考虑两者的时间耦合关系，将其等价转化为马尔可夫决策模型，进而采用深度强化学习算法求解。马尔可夫决策过程通过状态随机转移有效考虑了电压管理模型中的不确定性变量。此外，针对具体的物理模型和控制变量类型，本文分别提出利用DDQN 算法求解长时间尺度模型的离散控制变量，利用MADDPG 算法求解短时间尺度模型多逆变器的连续控制变量，达到算法和物理模型的有机统一。最后，本文基于IEEE 33 节点测试系统建立双时间尺度电压管理模型，通过算例验证本文模型和算法具有更优异的求解精度和鲁棒性。

1 双时间尺度电压管理模型与算法

1.1 双时间尺度电压管理模型

有载调压变压器（on-load tap changer，OLTC）和电容器组（capacitor banks，CB）的动作依靠机械设备，其动作时间尺度为小时级。可再生能源发电设备中的逆变器具有响应速度快、可连续动作等特点。本文设定短时间尺度（分钟级）的控制对象为光伏与风机的逆变器，长时间尺度（小时级）控制对象为OLTC 与CB。t时段的建模和求解过程如下所示：

1）长时间尺度的电压管理模型：在优化区间内（本文设置优化区间为1 d，并以小时为时间单位，即时段T=24）求解OLTC 与CB 在t时段的控制策略。优化目标为最小化所有时段每个节点电压与给定值之差的绝对值之和。

2）短时间尺度的电压管理模型：将t时段等分为K个子时段（本文设每时段为1 min，故K=60）。基于t时段OLTC 与CB 的状态求解第τ个子时段内逆变器的控制策略，优化目标为最小化每个节点电压与给定值之差的绝对值之和。

在训练阶段，首先训练短时间尺度神经网络，长时间尺度神经网络的训练需要借助短时间尺度模型来计算其奖励。在应用阶段，长时间尺度模型先做决策，获得OLTC 与CB 调度策略。在该时段内每一子时段，短时间尺度模型根据OLTC 与CB 状态进行决策，实现电压实时管理。

1.2 双时间尺度电压管理模型算法

目前，深度强化学习算法可以分为2 类：一类可以求解离散动作空间问题，如深度Q 网络（DQN）算法、DDQN 算法、rainbow 算法等；另一类可以解决连续动作空间问题，如DDPG 算法、MADDPG 算法等。

DDQN 算法引入了经验回放机制和2 个结构完全相同的估计和目标神经网络，避免了单个神经网络同时进行动作选择与目标Q 值计算而造成的过估计问题。因此，本文选择以DDQN 算法有效求解OLTC 与CB 在小时级与离散动作空间下的响应策略以实现长时间尺度电压管理。

与DDPG 算法相比，MADDPG 算法采用独立采样、统一学习的方法，不仅可降低集中训练的复杂度，还可以很好解决多智能体协作的任务。因此，本文选择MADDPG 算法求解光伏与风机智能体逆变器在连续空间上的瞬时协调控制策略，实现短时间尺度的电压管理。

2 基于深度强化学习算法的电压管理模型

配电系统的运行状态可以通过潮流计算获得。通过求解潮流模型可产生大量系统数据以供训练。本文采用节点注入潮流模型，如式（1）—式（3）所示。

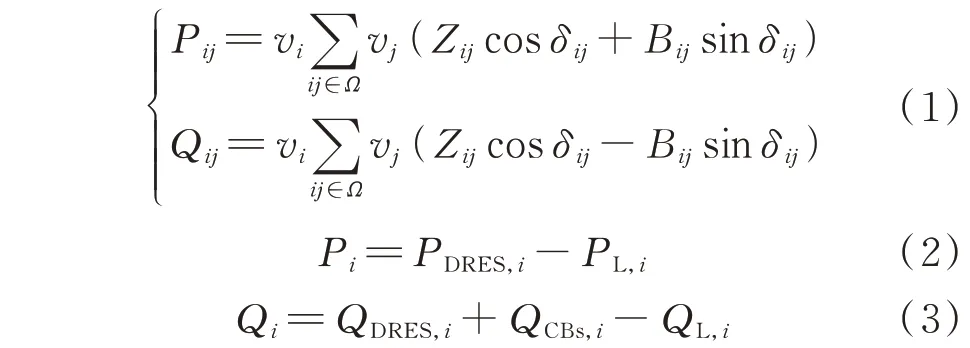
式中：Ω为配电网中所有支路的集合；i和j分别为支路ij的输入节点和输出节点；Pij和Qij分别为支路ij的有功功率和无功功率；Pi和Qi分别为节点i注入的有功功率和无功功率；Zij和Bij分别为支路ij的电导和电纳；δij为节点i与j之间的相角差；PDRES，i为节点i处可再生能源发电机组注入的有功功率；QDRES，i和QCBs，i分别为节点i处可再生能源发电机组和CB 注入的无功功率；PL，i和QL，i分别为节点i的负荷的有功功率和无功功率；vi为节点i的电压幅值。

2.1 基于MADDPG 算法的短时间尺度电压管理模型

在短时间尺度电压管理模型中基于t时段OLTC 和CB 的状态，求解逆变器在每个时段的最优控制策略。t时段中第τ个子时段的电压管理模型可描述为：

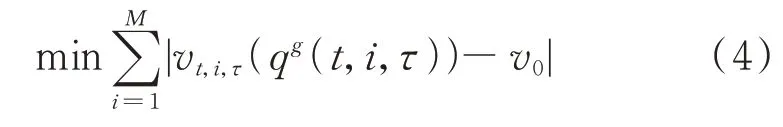
s.t. 式(1)至式(3)

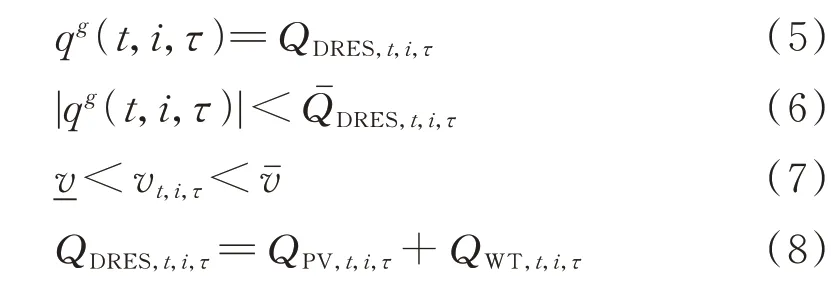
式中：M为配电系统中的节点数；vt，i，τ(qg(t，i，τ))为t时段中第τ个子时段节点i的电压幅值；qg(t，i，τ)为t时段中第τ个子时段的无功功率；v0为目标电压幅值；QDRES，t，i，τ和QˉDRES，t，i，τ分别为t时段中第τ个子时段节点i处可再生能源发电装置输出的无功功率及其上限；QPV，t，i，τ和QWT，t，i，τ分别为t时段中第τ个子时段节点i处光伏和风机逆变器所产生的无功功率；vˉ和-v分别为节点i电压幅值的上限和下限。

上述电压管理模型可建模为马尔可夫决策过程，t时段中第τ个子时段的马尔可夫决策过程具体描述如下：

1）短时间尺度状态空间Sd：状态空间应包括学习环境中所有智能体的观测状态。每个智能体的状态信息包括当前智能体的出力情况与上一时段调压设备的状态。

2）短时间尺度动作Ad：动作空间为学习环境中多个智能体的可以采用的动作。τ时段光伏智能体和风机智能体动作为其各自的无功功率。

3）短时间尺度奖励Rd：将优化目标与约束条件映射为奖励函数。以光伏智能体为例，τ时段光伏智能体奖励RPV，t，τ应包括τ时段电压偏差（即优化模型的目标函数）与系统运行约束条件的违规惩罚，可表示为：

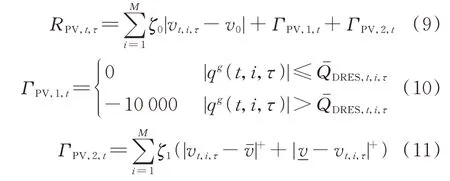
式中：ζ0为节点电压偏离基准电压的惩罚系数；|·|+为取正函数；ζ1为节点电压超过给定上限和下限的惩罚系数，且满足|ζ1|≫|ζ0|；ΓPV，1，t和ΓPV，2，t分别为约束式（6）和式（7）的违规惩罚参数。

光伏智能体和风机智能体相互合作以控制全局电压。因而，其两者奖励函数具有相同的形式，根据式（9）—式（11）可得风机智能体的奖励函数。

2.2 基于DDQN 算法的长时间尺度电压管理模型

长时间尺度电压管理模型中OLTC 与CB 的控制策略需考虑优化时段内可再生能源出力的不确定性。因此，假定在t时段内光伏与风机出力功率为随机变量，可将长时间尺度电压管理描述为随机优化模型：

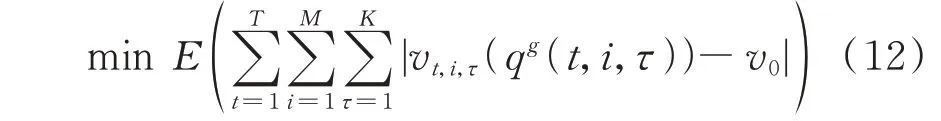
s.t. 式(1)至式(3)，式(5)至式(8)

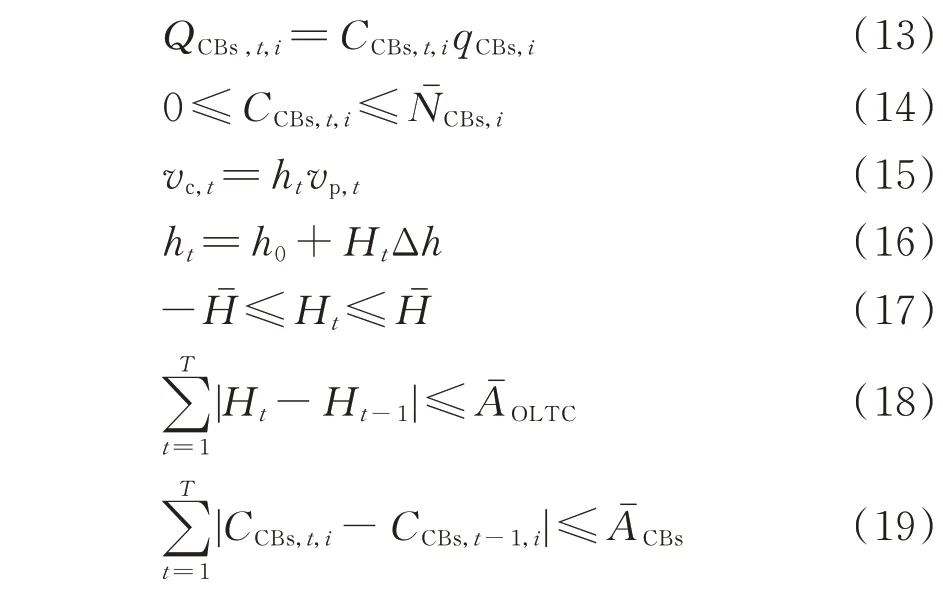
式中：E(·)为数学期望函数；CCBs，t，i和CBs，i分别为t时段内节点i处的CB 的投切组数和总组数；qCBs，i为节点i处CB 的单位组数的无功功率；AˉCBs为CB优化周期动作次数上限；vc，t为t时段内初始时段安装OLTC 节点1 的电压，一般为固定值1；vp，t为t时段平衡节点的电压，用于节点的电压计算；Δh和h0分别为OLTC 的相邻挡位调节变化量和初始电压调整率；OLTC为OLTC 优化周期动作次数上限；Hˉ为OLTC 档位的最大值；Ht和ht分别为t时段OLTC 的档位和电压调整率。

将上述随机优化模型建模为马尔可夫决策过程，具体如下：

1）长时间尺度状态空间Sc：在长时间尺度中需要采用期望和标准差来刻画t时段内分布式可再生能源出力情况。因此，t时段的状态包括可再生能源的发电情况、上一时段OLTC 与CB 的状态、可再生能源的期望值与标准差和调压设备在周期内的动作次数。

2）长时间尺度动作空间Ac：长时间尺度的动作空间应包含长时间尺度调压设备OLTC 和CB 的动作。

3）长时间尺度奖励Rc：当t时段不满足一个周期内OLTC 与CB 的动作次数约束时，奖励为一个绝对值很大的负数ϕ；反之，其为t时段中第K个子时段，M个节点的电压偏差之和与K个子时段惩罚之和的总和，表达式为：

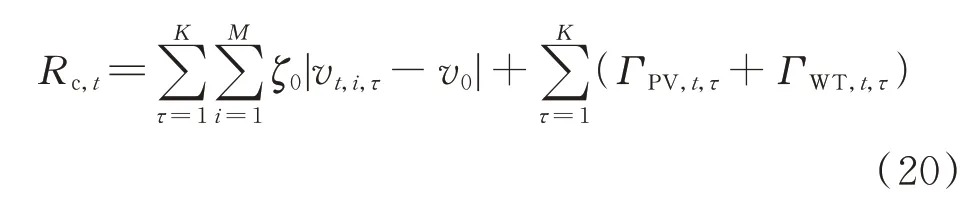
式中：ΓPV，t，τ和ΓWT，t，τ分别为t时段中第τ个子时段的光伏和风机智能体的约束违规惩罚，其中，ΓPV，t，τ=ΓPV，1，t+ΓPV，2，t。

2.3 电压管理深度网络训练方法

在实际应用中，短时间尺度的逆变器调度策略属于在线优化，可实时读取当前状态，调用MADDPG 算法演员网络，获得实时调度策略。长时间尺度（小时级）的调度策略为离线优化，调用DDQN 算法目标Q 网络，获取长时间尺度调度策略。基于此，长时间尺度基于可再生能源发电出力预测值，获取一天的状态，并调用目标Q 网络获取调度策略。双时间尺度电压管理模型中的DDQN算法与MADDPG 算法的神经网络更新过程如附录A 所示，双时间尺度模型如附录A 图A2 所示。

3 算例与结果

3.1 参数设置

以IEEE 33 节点标准配电系统为基础构造测试系统，对所提方法的可行性与有效性进行验证。系统的基准电压为12.66 kV，在标准系统中分别接入4 组光伏机组和2 台风机，其接入位置如图1 所示，容量如附录B 所示。其中，各节点的负荷根据原始IEEE 33 节点标准配电系统的负荷进行等比例分配。OLTC 安装在节点1 与节点2 之间，共有11个调节位置，每个抽头的调节率为1%。节点33 处安装有5 组电容器，每组的无功功率为60 kvar。考虑实际运行需要，设置OLTC 与CB 优化周期内动作次数上限分别为4 和5。

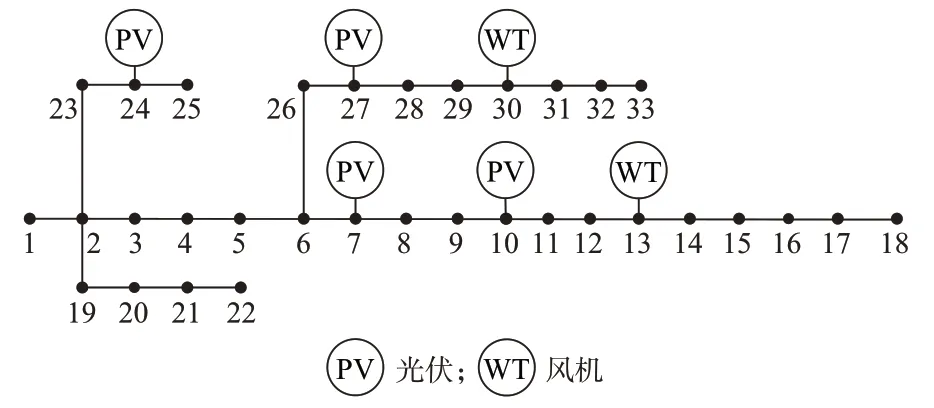
图1 IEEE 33 节点系统结构Fig.1 Structure of IEEE 33-bus system

本文在长时间尺度的电压管理模型中考虑了光伏与风机出力的不确定性。假设光伏和风机出力随机变量的分布由预测值和预测误差构成。光伏与风机出力的期望为其预测值。假设光伏出力预测的方差为其期望的3%，风机出力预测的方差为其期望的5%。随机抽样生成1 020 组场景，其中，1 000 组场景用于后文随机优化模型的策略求解，20 组对所得策略进行验证。此外，非线性潮流方程通过调用Pypower 包求解。

3.2 训练过程

所提模型的求解算法主要包括DDQN 算法与MADDPG 算法2 个部分。

MADDPG 算法中设置光伏和风机逆变器两类智能体。每个智能体的演员网络为策略选择网络，当该网络得出的策略奖励值趋于稳定时，代表该智能体深度网络收敛。训练过程中，设定演员网络的学习率为0.001，评论家网络的学习率为0.002。衰减因子γ为0.9，小批量采样规模为100，样本池内样本总量为10 000，观测步数为1 800。电压违规惩罚因子ζ1与ζ0分别为-1 000 和-2。设定动作探索噪声随着训练步数逐渐减小，初始噪声服从N(0，1)的正态分布。当训练步数大于观测步数时，噪声服从N(0，0.995z)的正态分布，其中，z为开始训练的步数。训练过程如图2 所示。

本文以DDQN 算法求解长时间尺度OLTC 与CB 的控制策略。在DDQN 神经网络训练过程中，本文设定经验回放机制的样本存储量为10 000，每次小批量采样规模为100；初始探索率为0.1，最终探索率为0.001，探索步数为5 000；学习率取0.001；每训练10 次更新一次目标Q 网络参数，惩罚因子ϕ为-100 000。训练过程如图2（c）所示。

由图2（a）和（b）可知，光伏智能体与风机智能体的演员网络分别在训练4 000 步和3 500 步时达到了收敛状态。随着训练步数的增加，2 类智能体演员网络的奖励分别收敛于-0.632 与-0.562。由图2（c）可得，在12 000 步时DDQN 算法神经网络达到收敛状态。在与环境的不断交互学习中，奖励值最终收敛于-1.212。最优策略的奖励收敛于-1.212而非奖励最大值-1.205，其差值可看作可再生电源出力不确定性所带来的风险成本。

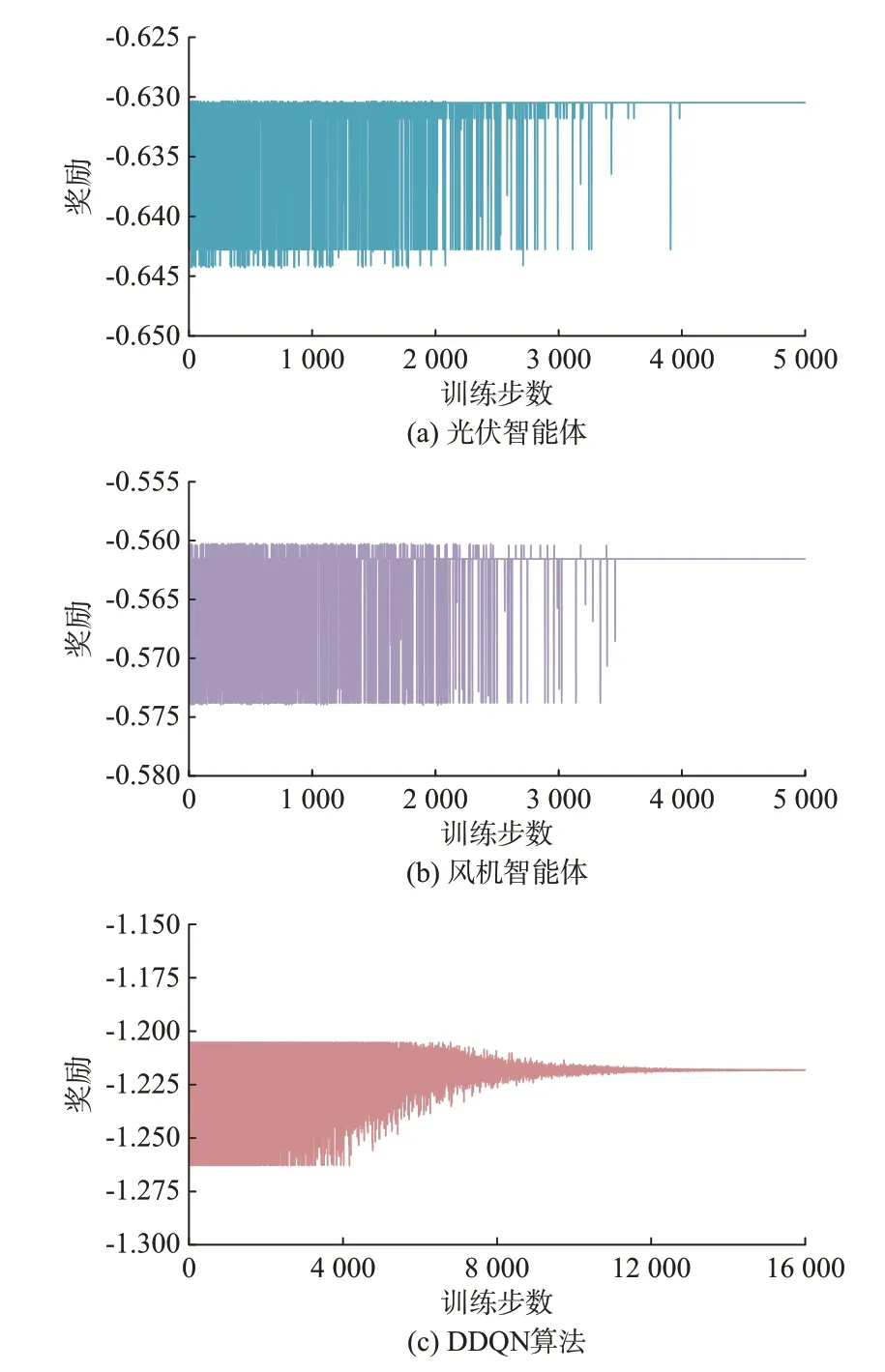
图2 深度强化学习算法的神经网络训练过程Fig.2 Neural network training process of deep reinforcement learning algorithm

3.3 算例结果与分析

为进一步研究所提出的模型与方法的有效性，本部分设置了3 种模式进行对比分析，具体如下：

模式0：不进行任何优化管理。

模式1：基于随机优化算法求解双时间尺度配电系统电压管理策略，模型见文献［9］。

模式2：本文所提算法，基于DDQN 算法求解长时间尺度电压管理模型，基于MADDPG 算法求解短时间尺度的电压管理模型。

采用3.1 节随机生成的20 个场景对上述3 种模式所得策略进行验证。3 种模式的测试结果如表1所示。违规时段数表示优化周期内24 个时段中存在电压违规现象的时段个数；平均电压偏差为33 个节点24 个时段电压偏差的平均值；电压最大爬坡和最小爬坡分别为各节点24 个时段最大电压变化和最小电压变化。

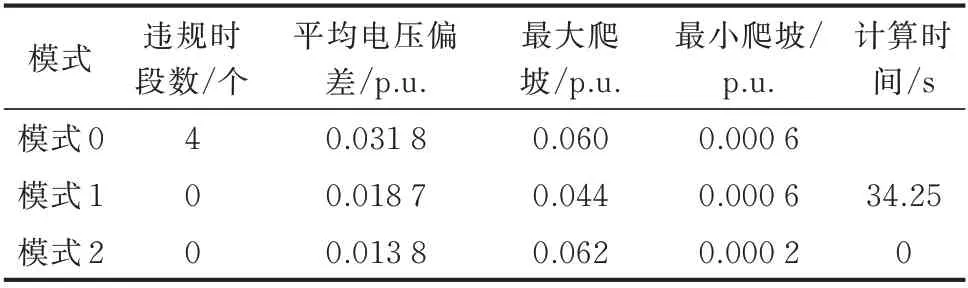
表1 优化结果对比Table 1 Comparison of optimization results

从表1 可知，模式1 和模式2 所得策略均不存在电压违规现象。与模式1 相比，模式2 优化后的电压偏差更小，仅为0.013 8，并可通过训练好的神经网络实时决策得到。

为更加直观地对比模式1 与模式2 的优化结果，以模式0 中存在电压越限的07：00 和20：00 时的数据为例，展示3 种模式所得各节点电压，如图3（a）和（b）所示。由图3 可知，模式1 与模式2 都能有效控制配电系统电压运行在安全范围内。与模式1 相比，模式2 的优化结果更加靠近基准电压值且电压幅值波动更加平缓，因而本文所提算法在电压偏差控制上表现更好。

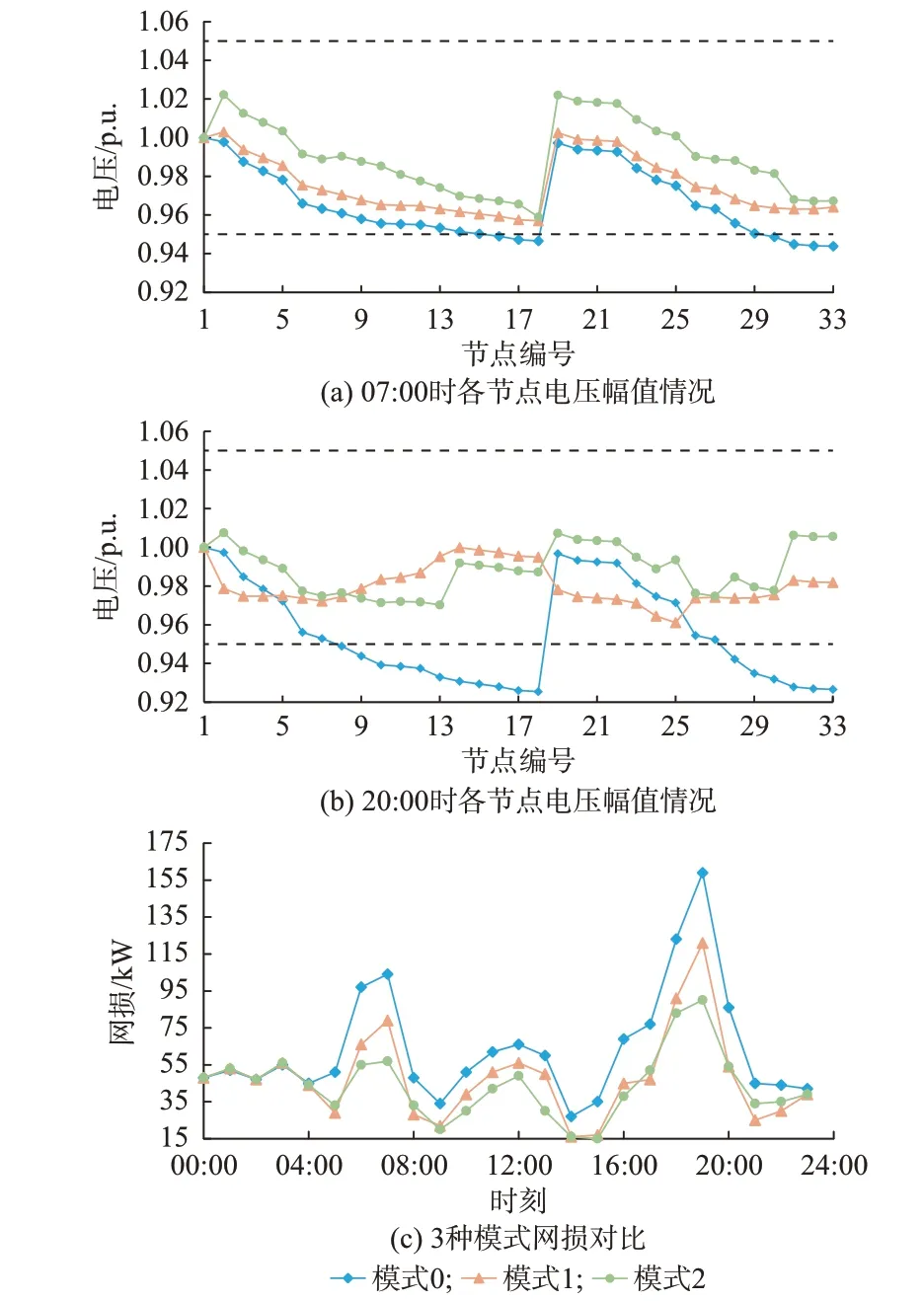
图3 3 种模式电压优化结果对比Fig.3 Comparison of voltage optimization results in three modes

为进一步分析所提方法的优越性，拟对比各种运行策略下的系统网损，对比结果如图3（c）所示。由图3（c）可知，本文所提方法在3 种模式中系统的网损最低。与模式1 相比，模式2 的平均网损降低了8.67%，这是因为模式2 下的节点电压靠近基准电压，且其幅值变化平缓，而网损与相邻节点之间的电压差成正相关，一定程度上降低了系统网损。由此可知，本文所提策略在保证配电系统安全运行的基础上，可间接有效提高配电系统运行的经济性。

3.4 算法鲁棒性分析

本部分设置极端场景以验证上述模式1 和模式2 所得策略的鲁棒性。假设在t时段中，每个时段可再生能源出力所满足的条件为：

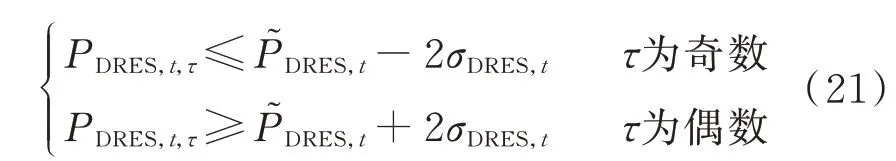
在此极端场景下，验证2 种模式下电压偏差情况。通过仿真模拟，模式1 的平均电压偏差为0.021 9，模式2 下的平均电压偏差为0.014 2。因此，模式2 在面对不确定性环境具有更好的鲁棒性。

相对于DDPG 算法，MADDPG 算法可以有效解决多个智能体的交互问题，并具有鲁棒性。为进一步分析所提MADDPG 算法的鲁棒性，本文设置了模式3，利用基于DDQN 算法求解长时间尺度配电系统电压管理策略和基于DDPG 算法求解短时间尺度的配电系统电压管理策略。

DDPG 算法神经网络训练过程中，设定演员网络的学习率，评论家网络的学习率、衰减因子γ，目标演员网络与目标评论家网络的更新因子з与MADDPG 算法相同；小批量采样的规模为80，样本池内样本总量为10 000，观测步数为1 500，动作探索噪声随着训练步数逐渐减小，初始噪声服从N(0，2)的正态分布。

为验证MADDPG 算法的鲁棒性，设置4 种光伏故障情况来测试模式2 和模式3 所得策略的性能。假设光伏智能体链路故障时无法提供有功和无功功率支撑。故障情况具体如下：

故障0：无故障发生。

故障1：节点24 的光伏机组故障。

故障2：节点24、节点10 的光伏机组故障。

故障3：节点24、节点1、节点7 的光伏机组故障。

针对上述4 种光伏机组故障比较DDPG 算法与MADDPG 算法的性能，结果如表2 所示。

表2 4 种故障下的优化结果对比Table 2 Comparison of optimization results in four types of faults

由表2 可知，在故障0 与故障1 的情况下，模式2与模式3 所得电压偏差较小。在故障2 与故障3 的情况下，由于光伏智能体信息数据丢失严重，与模式2 相比，模式3 不能很好地处理，出现了电压违规现象，且平均电压偏差较大。由此可知，MADDPG 算法在面对光伏机组故障时具有更好的鲁棒性。

4 结语

本文针对配电网内调压设备不同时间响应特性，建立双时间尺度的电压管理模型，在有效考虑可再生能源出力不确定性的基础上，将电压管理模型等价转化为马尔可夫决策模型。针对多种电压控制对象的动作与响应等技术特点，利用深度强化学习DDQN 算法和MADDPG 算法分别求解长时间尺度模型的离散控制变量和短时间尺度模型的连续控制变量，实现了配电系统电压管理的实时决策。与传统随机优化算法相比，采用本文所提方法可得到更优异的电压管理效果，同时在面对随机环境时具有更好的鲁棒性。

在后续研究中，拟采用随机过程对电压管理模型的随机变量进行建模，通过考虑时序上的关联性来降低本文策略的保守性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。