电喷雾推力器锥射流形成的电流体力学仿真
2022-07-04程玉峰王伟宗张金瑞刘昱涵蔡国飙
程玉峰,王伟宗,张金瑞,刘昱涵,蔡国飙
(北京航空航天大学宇航学院,北京 102206)
电喷雾推力器是一种推力小、比冲高、可长时间连续运行的微推进系统,其结构简单、体积小、推力精度高,格外适用于微纳卫星以及需要高精度姿态控制的太空任务,例如引力波探测计划[1]。近年来,随着微纳卫星的迅猛发展以及国内天琴计划与太极计划的提出,电喷雾推进技术的研究受到国内外广泛关注。
电喷雾推力器的物理原理为液体的电喷雾现象。在电喷雾过程中,电介质液体或离子液体在静电场作用下液面会累积大量电荷,带电液面在库仑力作用下变形为锥形。1964年Geoffrey Ingram Taylor首次从理论上对该过程进行推导,基于锥液面电场力与液体表面张力相平衡的条件,并计算出锥半角为49.3°,因此该锥也被称为泰勒锥[2],锥尖处因电场强度最大会引出一股射流,射流末端由于不稳定破碎产生液滴或离子。图1为典型的电喷雾推力器结构,其基本原理为在毛细管与抽取极板间加载高电压以产生强电场,液体从毛细管流出并在强电场的作用下形成锥射流,带电液滴或离子在电场的作用下进一步加速喷出产生推力。由于液滴及离子间的库伦排斥作用,在射流末端形成锥形荷电喷雾,这种荷电锥形喷雾是一种特殊的等离子体,而较大的喷雾锥角不仅会降低有效推力,还会加速抽取极板的腐蚀与推力器的失效[3]。
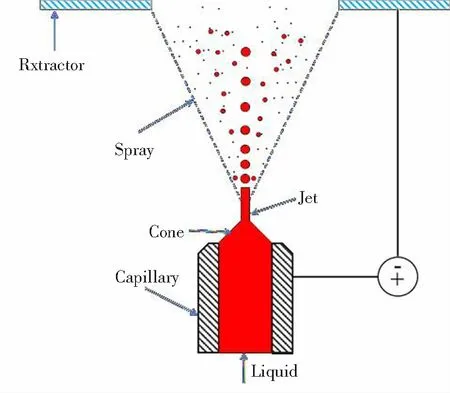
图1 电喷雾推力器示意图Fig.1 Schematic of the electrospray thruster
Geoffrey Ingram Taylor最先建立起电喷雾过程理论框架,并在上世纪六十年代中期首次提出漏电介质模型以描述液滴在稳定电场下的形变[2]。随后Taylor与JR Melcher扩充发展了电流体力学理论[4],提出了更为完善的Taylor-Melcher漏电介质模型[5],得到了广泛应用。Orest Lastow等人借助计算流体力学(Computational Fluid Dynamics:CFD)软件并利用漏电介质模型模拟了稳定锥射流模式的形成[6];Lopez-Herrera等人借助Gerris软件并使用VOF方法,发展了一套考虑电荷守恒及电荷迁移的电流体求解器用以模拟电喷雾过程[7];麻省理工学院的Ximo Gallud Cidoncha使用有限元方法求解了包含电荷蒸发的Taylor-Melcher漏电介质模型,得到稳态纯离子发射模式下的锥液面形状[8]。目前国内对电喷雾过程的仿真研究大多为静电雾化[9]、静电纺丝[10]及静电喷印[11]等,而对电喷雾推力器和电喷雾锥射流过程的电流体力学仿真研究较为匮乏。
目前国内外电喷雾锥射流过程的CFD仿真工作工质多为低电导率液体,电导率在10-5S·m-1以下。日本东北大学的川谷康二和高奈秀匡对电导率为0.365 S·m-1的EMI-BF4离子液体进行了数值仿真研究[12],但模型未考虑空间电荷对空间电场的影响,仿真中抽取电压小于实验中抽取电压的1/10。高电导率离子液体下的电喷雾过程,因锥液面电荷密度更大、液锥内部速度及电学参数分布更为复杂,空间电荷对锥射流形成演化的影响更大,使得数值计算更容易发散,这对数值仿真的计算量提出了更高要求[13]。此外,使用CFD的手段无法模拟出离子液体的离子发射模式。
本文借助FLUENT有限体积仿真软件中的用户自定义接口,以二次开发的形式编写代码(UDF文件)添加电场及电荷守恒方程,实现空间电荷的引入,并考虑了电流对电荷分布的影响。通过本文模型计算得到了锥射流的形成演化以及电荷、电势和流场的分布,与未考虑空间电荷的理想电介质模型得到的仿真结果进行对比,分析两种模型的主要差异。
1 研究方法
电喷雾过程的物理模型主要包括流体和电场两部分,其中电场部分除本文使用的模型,还将介绍常用的理想电介质模型。本研究包含两种流体,分别是空气和作为推进工质的庚烷液体,并采用VOF方法对两种流体的交界面进行追踪模拟。
1.1 控制方程
1.1.1 流体方程
流体部分采用直接数值模拟的方法进行计算,描述流体运动的方程主要包括质量守恒方程与Navier-Stokes(N-S)方程:
∇·u=0
(1)
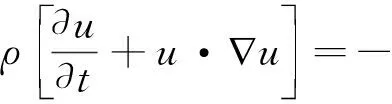
(2)
其中电场力Fe与表面张力FST作为源项加在N-S方程的右端。ρ为流体密度,u为流体速度矢量,p为压强,μ为粘滞系数。
表面张力采用连续表面力模型(Continum Surface Force:CSF):
FST=γκn
(3)
n为液体界面法向方向,通过对流体的体积分数α求梯度得到:
n=∇α
(4)
κ为表面曲率,通过对单位法向矢量求散度得到:
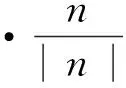
(5)
因电喷雾推力器的工作环境为太空,且重力对液滴的影响远小于电场,因此N-S方程中不考虑重力。
1.1.2 电场方程
本文模型的电场方程包含未简化的电荷守恒方程(式(6)),其中u为液体流速,ρe为自由电荷密度,σ为液体电导率,ε为液体的介电常数,液锥内部的导电电流σE持续向液面输送电荷,而液面处对流电流ρeu会影响液面电荷密度的分布。式(7)为电势的泊松方程,方程右端引入的电荷密度通过影响空间电势的分布,进而影响空间电场分布、电荷分布以及锥液面的受力,即空间电荷对锥射流形成演化过程的影响。电场为电势的负梯度(式(8))。式(9)为液体所受电场力,第一项为静电场力,第二项为与液面处介电常数ε的跃变有关的电极化力。[13-14]
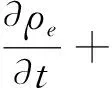
(6)
-∇·(ε∇φ)=ρe
(7)
E=-∇φ
(8)
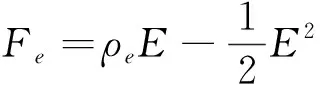
(9)
理想电介质模型的电场部分只求解电势的拉普拉斯方程(10),电势分布不受空间电荷影响,极化电荷密度ρP由高斯定律(11)求得,电场的求解同式(8),式(12)为液体受到的体积电场力。[6][15-16]
-∇·(ε∇φ)=0
(10)
ρP=-ε0∇·(∇φ)
(11)
Fe=ρPE
(12)
其中式(10)与式(11)物理意义不同。计算域中存在液体与空气两相,介电常数均为各向同性的。当只在液体相中或大气相中时,介电常数处于两个Nabola算子之间或之外并无区别;但在液体与大气界面,两相介电常数不同,介电常数梯度不为0,介电常数处于两个Nabola算子之间或之外得到的结果不一致。实际上,式(10)的物理意义是介质界面不存在自由电荷ρe,电位移矢量-ε∇φ在介质界面连续,即散度为0;式(11)的物理意义是介质界面在外加电场的作用下有极化电荷ρP积累,极化电荷会影响空间电场分布,使得介质界面处法向电场不连续。仿真计算中,式(10)在给定电势边界条件及空间介电常数分布下计算出空间电势分布,式(11)通过空间电势分布利用高斯定律计算出介质界面电荷密度分布。
本文模型中的电荷守恒方程考虑了液体的电导率属性,可更为真实地反映液体内导电电流σE及对流电流ρeu对液面电荷密度分布的影响,相比理想电介质模型存在诸多优势。对于理想电介质模型的电势方程(式(10)),常用的商业CFD软件已有成熟的模块用于求解。但本文模型中包含的电荷守恒方程只能通过自编程的方式引入,且通过电荷守恒方程求解的空间自由电荷密度与电势方程(式(10))耦合,此外,对较高电导率液体的电喷雾仿真,射流宽度更细,电荷密度分布的梯度变化更大,进一步增加了模型求解的复杂度与计算发散的可能性。因此,通过本文模型数值仿真电喷雾过程时需找到最合适的电压、流量等工况参数,收敛参数与网格疏密分布等,才能得到更合理且准确的仿真结果。
1.2 仿真设置
进行数值计算前需要构建相应的计算域并划分结构化网格。为节省计算量,本文将计算域简化为柱对称长方形区域,如图2(a),其中红色区域为液体初始位置,黑色区域为毛细管壁(加载正电势),白色区域为空气域。边界条件分为静电边界条件和力学边界条件,表1(注:图2(a)中1~6方向为“z”方向,1~4方向为“r”方向)列出边界条件及尺寸参数,1~6为对称轴,取纽曼边界条件,使电势、压强等物理参量在对称轴处连续;1~2为速度入口,液体在流动过程中由于固体壁的毛细力作用,到达固体壁顶端后会形成类似抛物线型的速度分布,且液体流速较小,r方向的速度差异相比于电场力与表面张力对速度的影响可忽略不计,速度入口设为均匀速度入口条件,与相关研究一致[6,13,15];3~4、4~5为计算域常压边界,“P=0”表示表压为0,流体可自由出入;5~6为抽取极板(加载零电势),同时也是常压边界,流体可从此处流入流出;3~8,7~8,7~2设为无滑移壁,电势取狄利克雷条件。计算域的离散化通过划分结构化网格实现,仿真中使用的网格如图2(b)所示,网格单元宽度最小为1.7 μm,总网格数为23125。

(a)

(b)图2 (a)仿真计算域设置示意图(b) 仿真计算的结构化网格Fig.2 (a) Schematic of the simulation domain (b) Structured mesh of the simulation
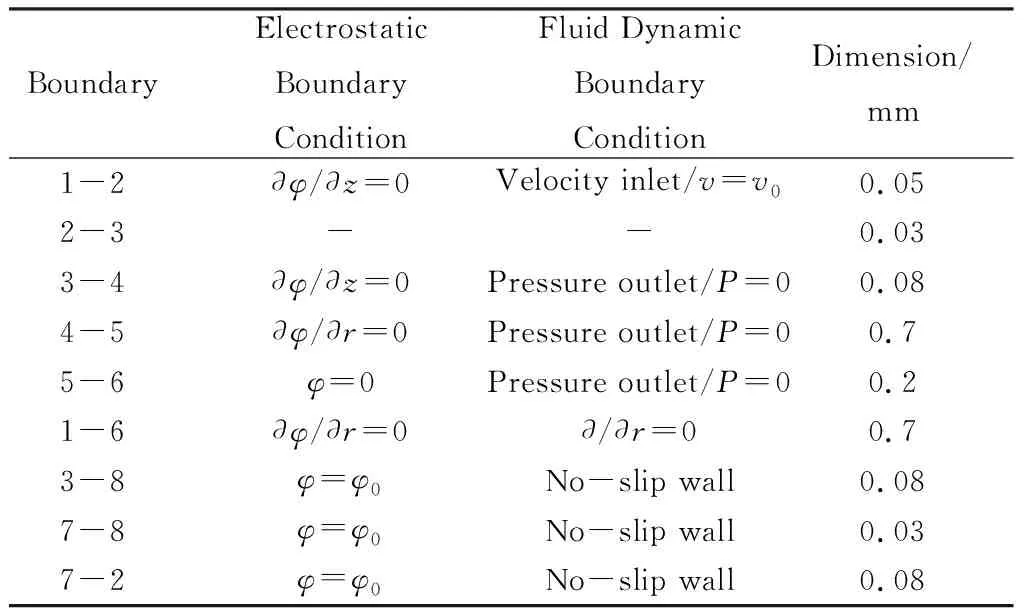
表1 计算域的边界条件及尺寸Tab.1 Boundary condition and the dimension of the simulation domain
本研究对大气环境下的电喷雾过程进行模拟,推进剂庚烷电导率值取为离子液体EMI-Im的1/100,约为0.009 2 S·m-1(EMI-Im的电导率约为0.92 S·m-1),以验证本文模型能否模拟高电导率液体的电喷雾过程。为更接近真空下的环境,空气电导率取值趋于零,使其不影响电荷、电场等的空间分布。仿真中发现当施加电压φ=4 kV,流量为5.5×10-10m3·s-1(对应入口流速v0=0.07 m·s-1)时,得到的仿真结果最好,与实验结果最接近[13]。因此,若未经额外说明,以下结果均在施加电压为4 kV,流量为5.5×10-10m3·s-1的工况下所得。
2 结果与讨论
2.1 网格无关性验证
为验证仿真结果独立于网格,本研究共设计3套网格,网格数分别为20 645,23 125,44 707,网格单元最小宽度分别为2.5,1.7,0.85 μm。仿真中发现,由于液体电导率较高(0.009 2 S·m-1),即使采用小于0.85 μm的网格单元宽度,射流直径仍小于网格单元宽度,无法准确得到射流宽度,因此未采用射流宽度作为网格无关性验证参数。而射流电流作为评估电喷雾推力器推力性能的重要参数,还能反映液体在电喷雾过程中的电离效率、液滴的平均荷电量及液面电荷密度大小;初始时刻最大场强为仅在外界电势边界条件下计算得到的空间最大场强,决定了锥射流的形态及电流大小。因此本文选用射流电流及初始时刻最大场强作为网格无关性验证参数。其中射流电流通过对空间中飞行的带电液滴产生的瞬时电流进行时间平均得到。
在施加电压为4 kV,流量为5.5×10-10m3·s-1时,使用三套网格计算得到的射流电流分别为240,223,221 nA,初始时刻最大场强均为3.884×107V·m-1。第二套网格与第三套网格计算结果吻合较好,认为第二套网格基本满足网格无关性验证要求,因此本文选用第二套网格能得到更准确的结果,以节省计算量。
2.2 锥射流的形成与演化
仿真中电喷雾过程分为3个阶段,首先液体在法向电场力、切向电场力、表面张力、惯性力、粘性力等力作用下达到平衡形成锥形;随后锥尖处累积大量电荷,且该处电场强度最大,当所受电场力超过表面张力时,便引出一股射流;最后射流末端由于毛细管Rayleigh不稳定性而破碎形成液滴[17]。
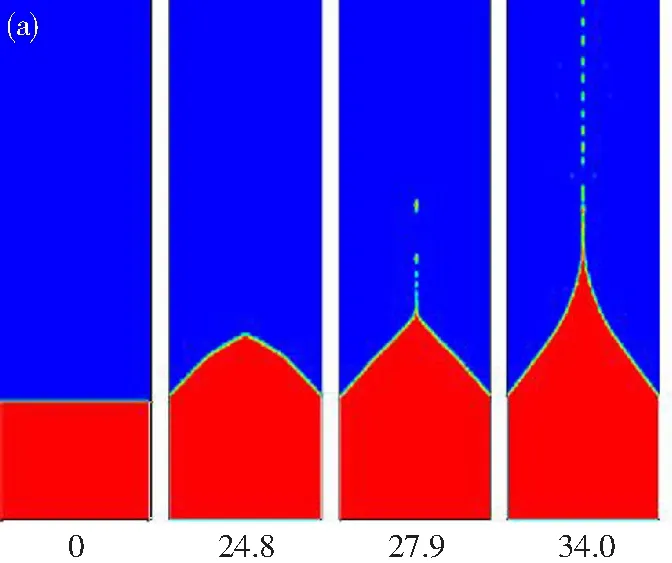
当毛细管和抽取极板间施加电压为4 kV,流量为5.5×10-10m3·s-1时,两种模型下锥射流形成演化的仿真结果如图3。本文模型在24.8 μs左右形成稳定泰勒锥,在34.0 μs左右射流充分发展并稳定发射液滴,射流宽度、液滴大小及液滴充分发射的时间尺度与UCLA的Peter L.Wright等人在实验中观察到的结果较为接近[3];理想电介质模型在39.4 μs左右形成泰勒锥,直到161.0 μs左右射流仍在延长,且未破碎产生液滴。本文模型从形成泰勒锥到产生射流并形成稳定发射液滴的时间均短于理想电介质模型,锥半角更接近49.3°,射流更细、射流长度更短。主要原因是本文模型下,电场对液面行为的影响占主导,液面对电场响应更强;而理想电介质模型下液体的惯性力对液面行为的影响占主导。
(a)

(b)图3 两种模型下的锥射流演化过程(a)本文模型(b)理想电介质模型Fig.3 Cone-jet modes of the two models(a) Model proposed in this paper (b) Simplified model.
2.3 锥射流的电荷与电势分布
由2.1.2知,两种模型的差异主要体现在电场部分。在数值求解过程中,本文模型是通过电荷守恒方程(式(7))求得电荷密度,液面电荷来源于液锥内传导电流σE的输送,而式(7)中对流项∇·(ρ)eu)描述了液面电荷在电场作用下的流动。如图4(a),液面电荷在切向电场作用下流向液锥尖端并进入射流段,因此锥尖及射流段电荷密度最大,可达1 000 C·m-3以上,计算得到的最大电荷密度值与Lopez-Herrera等人得到的电荷密度值数量级一致[18]。此外,从图4(a)中可以看出电荷密度在锥尖与射流段的梯度变化较大,仿真中发现电导率取值更大时,计算得到的电荷密度分布存在明显误差,主要原因是电荷密度梯度过大,导致计算发散,造成明显的计算误差。而理想电介质模型是通过高斯定律(式(12))求得电荷密度,将液体当成理想电介质,电荷来源于介质交界面在强电场下感应产生的极化电荷,未考虑电荷在液面的流动及液体的导电性。如图4(b),液面电荷主要分布于射流末端及锥液面,这些区域的电场跃变较大,而在射流段,极化电荷较少,且不存在从锥液面流入的电荷。此外,比较两种模型下求解的电荷密度分布,发现本文模型下电荷密度远远大于理想电解质模型,可知对于较高电导率(0.009 2 S·m-1)的液体,液面在外加电场下感应产生的电荷主要来源于导电电流σE与对流电流ρeu,与液体的电导率属性相关,而与介电常数大小相关的极化电荷密度可忽略不计。
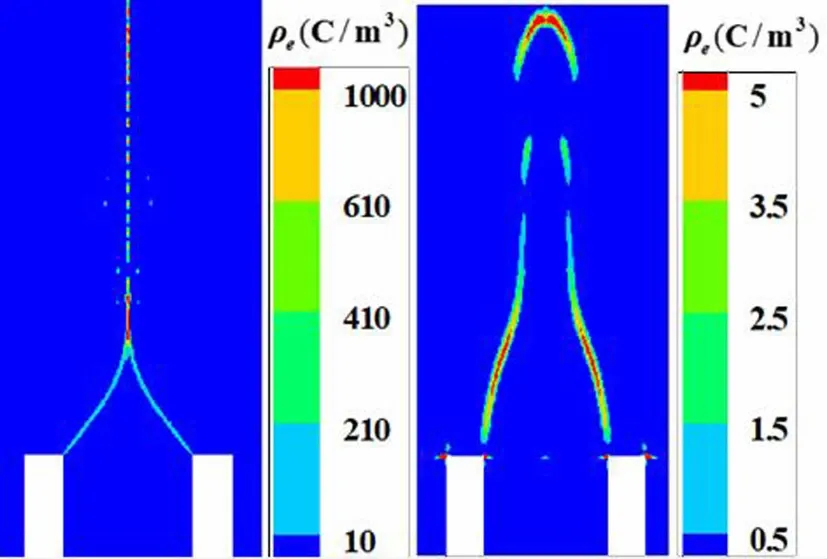
(a) (b)图4 两种模型下的电荷密度分布(a)本文模型(b)理想电介质模型Fig.4 Charge density distribution of the two models(a) Model proposed in this paper (b) Simplified model
图5为两种模型分别计算得到的空间电势分布,图5(a)中射流段存在电势降落,射流段及液滴对空间电势分布存在较大的扰动,这是因为其对应求解的电势方程为泊松方程,考虑了电荷对电势分布的影响。电导率越大,越少的电势降落发生在射流段,越多的电势降落用于加速带电液滴[19],因此使用电导率更高的液体作为工质,液滴喷出速度更高,推力器的比冲将更大。图5(b)对应求解的电势方程为拉普拉斯方程,未考虑电荷对电势分布的影响,因此空间电势分布并未发生变化。

(a) (b)图5 两种模型下的电势分布(a)本文模型(b)理想电介质模型Fig.5 Electrical distribution of the two models(a) Model proposed in this paper;(b) Simplified model
本模型考虑了液体的导电性以及电荷在液面的流动,因此液面电荷密度更大,液面及锥尖受到的电场力更大,形成泰勒锥的时间缩短,泰勒锥锥尖曲率更大,引出的射流宽度更小。由于液面的带电粒子持续流向射流段,使射流段电荷密度达到1000 C·m-3以上,促进射流不稳定破碎形成液滴,因此仿真中射流段较短,破碎形成的液滴电荷密度也在1000 C·m-3以上,在电场作用下进一步加速,在靠近抽取极板处速度可达150 m·s-1以上。
2.4 液锥内部的涡旋流场
在电喷雾的实验或仿真研究中,液锥内部的涡旋是很常见的物理现象[6][20],其产生的原因是剪切麦克斯韦张力作用在液面,将一部分液体拉向锥尖,但由于锥尖处射流过窄,这部分液体无法完全通过射流排出,剩下的液体便在液锥内部回流形成涡旋[21]。
图6(a)、(b)为流量取5.5×10-10m3·s-1,抽取电压取4 kV时两种模型得到的液体流场分布,本文模型未出现涡旋,而理想电介质模型在射流底部出现了涡旋。但将流量缩小十倍,取5.5×10-11m3·s-1时,使用本文模型得到的结果如图6(c),在液锥底部出现了明显的涡旋。相比图6(a),图6(c)中,由于液体流量较小,液锥锥角更大,液锥高度更小,因此液面法向指向液体内部的电应力更大,导致从毛细管管口流出的液体在该电应力的作用下洄流,从而液锥内部出现涡旋。UCLA的Henry Huh等人在仿真研究中通过改变流量观察涡旋的形成,发现流量越小,涡旋尺寸更大,生成速度越快[20]。因此可认为本文模型在流量取5.5×10-10m3·s-1时,由于流速过大,液锥锥角较大,液锥内流场未形成明显的涡旋。
此外,降低流量会对其他物理量(面电荷密度分布、电势分布等)造成一定影响,但主要影响局限于锥射流形态及内部流场;而改变电压会对各物理量(面电荷密度分布、电势分布,流场等)造成较大影响,低电压无法形成稳定的锥射流,高电压下会出现多股射流,计算易发散。对于分析流量及电压对其他物理参量影响的研究会是我们下一步的工作。

(a) (b) (c)图6 两种模型下的流场分布(a)本文模型(b)理想电介质模型(c)本文模型取Q=5.5×10-11 m3·s-1,φ=4 kVFig.6 Flow field distribution of the two models.(a) Model proposed in this paper (b) Simplified model (c) Model proposed in this paper as Q=5.5×10-11 m3·s-1 and φ=4 kV
2.5 两种模型在低电导率下的近似
理想电介质模型将液体看作不可导电的电介质,未考虑液体的电导率属性,液面电荷主要来源于介质在液面极化累积的电荷,液面电荷密度较低,液面也不存在电荷的对流,电场对液体的作用仅局限于锥液面及射流末端。对于电导率较低的液体,在外部电场下,其内部传导电流σE极小,可忽略不计,液面电荷同样主要为极化电荷,此时可使用理想电介质模型来求解其电流体力学过程。
图7(a)为将液体电导率设为0.92×10-6S·m-1,使用本文模型计算得到的结果,与图7(b)理想电介质模型得到的结果类似,射流宽度较大,在计算域内未发生破碎,且在射流发展过程中,泰勒锥均出现在距离毛细管口约0.1 mm处。主要原因是在低电导率下,内部传导电流σE与液面对流电流ρeu(液面流体流速较小)极小,对液面电荷密度贡献可忽略不计,使得电荷守恒方程(式(6))对电荷密度分布的影响较小,此外,由于液面电荷主要为极化电荷,而自由电荷密度ρe(式(7))较小,对空间电势分布影响较小,此时本文模型退化为理想电介质模型。
因此理想电介质模型由于其计算量小的优势,适用于电导率低于0.92×10-6S·m-1的液体,而本文模型既能用于仿真低电导率液体,在仿真高电导率液体时也能得到和实验相近的结果。
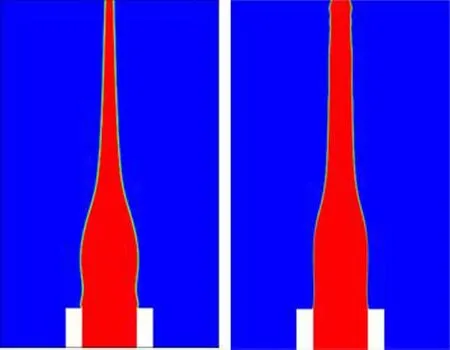
(a) (b)图7 使用低电导率液体时两种模型的比较(a)本文模型 (b)理想电介质模型Fig.7 Comparison of the two models when using liquids with low conductivity (a) Model proposed in this paper (b) Simplified model
3 结论
目前国内外针对电喷雾锥射流演化过程的仿真研究主要使用的模型为理想电介质模型或漏电介质模型,采用的液体也为低电导率液体,使用与本文类似的模型对高电导率液体的电喷雾锥射流演化过程开展的仿真研究尚属少数。本文将庚烷液体电导率设为EMI-Im离子液体电导率的1/100,研究本文模型是否适用于对高电导率液体的电喷雾过程中进行仿真,而仿真结果显示对于电导率为0.05 S·m-1及以下的液体,本文模型均能得到较好的仿真结果并可对各物理场(电场、流场、电荷密度、液体体积分数等)进行定量分析。改变电导率还在一定程度上定量地确定了理想电介质模型适用的电导率范围,仿真结果表明将液体电导率取为0.009 2 S·m-1时,理想电介质模型得到的结果偏差较大,而将液体电导率取为0.92×10-6S·m-1时,理想电介质模型与本文模型的仿真结果类似,因此理想电介质模型可对电导率小于0.92×10-6S·m-1的液体的电喷雾特性进行高效研究。
仿真中发现对于电导率为0.009 2 S·m-1的液体,锥射流演化速度较快,34 μs左右射流得到充分发展,稳定发射出大量液滴,所得射流宽度极细,小于1 μm,与文献[3]中的实验结果相近。此外,模型中加入电荷守恒方程,考虑了传导电流对液面输送电荷以及液面电荷的对流,仿真结果中射流段及液滴电荷密度大于1 000 C·m-3,液滴可加速到150 m·s-1以上,但离子液体电喷雾推力器发射的液滴或离子速度可达几千到上万m·s-1。本文下一步工作将进一步完善模型以及求解方法并深入研究高电导率液体的稳定电喷雾锥射流演化过程。
