关于运动量度的历史辩争——兼谈几位科学家的贡献

吴晓松 宋蒲泉

(重庆涪陵第五中学校 重庆 408000)

1 运动量度之一 动量的朔源

第一个提出运动物理量的是意大利科学家伽利略，当时欧洲已经完成文艺复兴运动，淹没已久的希腊和罗马文化得以重见天日，这不仅使文化和艺术得以复兴，也极大地促进了科学的繁荣．在这种背景下，伽利略通过对落体运动和打击现象的研究于1638年最早提出描述物体运动的量，即动量的概念，并把物体的速度和重量的乘积作为具体量度．值得说明的是当时重量和质量的概念并未区分．

在伽利略对动量研究的基础上，法国自然哲学家笛卡尔(图1)也从实验中认识到应该用物质与速度之乘积作为运动的量度，并进一步根据他的哲学思想来论证物质运动守恒：“上帝创造了广延(物质)，并把运动放进宇宙，此后就听其自然地运行．所以宇宙中的运动总量必定是个常数．”他说：“当一部分物质以两倍于另一部分物质的速度运动，而另一部分物质却是这一部分物质的两倍时，我们应该认为这两部分物质具有等量的运动，并且认为当一个部分的运动减少时，另一部分的运动就相应地增加．”这里初步形成了动量概念和动量守恒的思想．笛卡尔把物质间的作用归纳为挤压和碰撞，并根据他的实验总结出7条碰撞定律．但由于他没有赋予动量以矢量性，也不了解弹性和非弹性碰撞等概念，因此他的碰撞定律多数是错的，只有两条属于对完全弹性碰撞交换速度和完全非弹性碰撞的描述是正确的．

图1 笛卡尔(1596-1650)

荷兰科学家惠更斯在笛卡尔关于运动守恒的基础上仔细研究了弹性碰撞，并完整表述了运动量守恒的规律．特别是他赋予动量以矢量性，从而把矢量引入了物理学．

英国科学家牛顿站在前人的肩膀上于1687年发表的《自然哲学之数学原理》中，明确定义了动量这个概念，即运动的量是运动的量度，可由速度和物质的量共同求出．整体的运动是所有部分运动的总和．因此，速度相等而物质量加倍的物体，其运动量加倍；若其速度也加倍，则运动量加到4倍．至此动量的概念才被完整的建立起来．

2 运动量度之二 动能的挑战

动能的早期原型——活力，一开始也是作为一个运动守恒量被人们根据实验提出来的.荷兰科学家惠更斯在研究对心碰撞中除了指出动量具有方向外，在他发表的《物体在碰撞下的运动》一文中，还指出在弹性碰撞中∑mv2守恒，当时称为活力守恒．

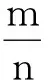
图2 莱布尼兹(1646-1716)

故有

可见，两个物体相同的运动的力表现为它们的质量与速度平方的乘积相等．同时莱布尼兹也看到，笛卡尔提出的用mv量度运动在某些情况下也是适用的，例如在杠杆、滑轮等简单机械装置中研究平衡问题的场合．因此，在1695年他又提出运动的力有两种量度，一种是“死力”，一种是“活力”，“死力”即相对静止的物体间的力，它可用物体的质量与该物体由静止转入运动时所获得的速度的乘积来量度，所以mv是“死力”的量度，而“活力”由mv2来量度．物体正是由于自身具有的活力，才成为活动的，永不静止的．因此，在自然界中真正守恒的东西正是总的“活力”(对于非弹性碰撞中活力减少这一事实，在莱布尼兹看来，活力并未损失，而是被物体内部的微小粒子吸收，微小粒子的活力增加了)．

3 达朗贝尔力的判决

莱布尼兹提出活力mv2作为运动的量度，挑战了之前把mv看作运动的唯一量度，引发了对两种量度的争论，促进了对运动的量度问题的研究．不少著名的科学家如伯努利、欧拉等都参加了这场争论．经过半个世纪，法国科学家达朗贝尔(图3)在1743年发表的《动力学论》一书的序言中指出了两种量度的等价性，认为之前的争论是一场咬文嚼字的争论，他指出双方实际上是从不同的角度描述了运动的守恒性．用现在的科学术语来说就是，力既可以通过动量来表示

图3 达朗贝尔(1717-1783)

又可以通过动能来表示

4 恩格斯能的总结

直到19世纪下半叶，能量概念和能量转化和守恒定律确立以后，恩格斯(图4)根据当时自然科学的成就，于1880-1881年间写了《运动的量度——功》一文，详细论述并分析了两种量度之争的历史，最后给出了这一争论的科学总结．恩格斯指出：“机械运动确实有两种量度，每一种量度适用于某个界限十分明确的范围之内的一系列现象．如果已经存在着的机械运动保持机械运动的形态而进行传递，那么它是依照质量和速度的乘积这一公式而进行传递的．但是，如果机械运动是这样传递，即它作为机械运动而消失，并以位能、热、电等等形态重新出现——如果它转变为另一种形态的运动，那么这一新形态的运动的量就同原来运动着物体的质量和速度平方的乘积成正比．

图4 恩格斯(1820-1895)

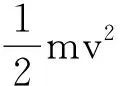
对于恩格斯的总结我们可以通过两个物体的非弹性碰撞来重新理解：质量分别为m1和m2的两物体，碰前的速度分别为v10和v20，碰后的速度分别为v1和v2，根据动量守恒和能量守恒有

m1v10+m2v20=m1v+m2v2

其中Δε为碰撞中内能的增量．第一个式子表明碰撞中一物体动量的减少量必定等于另一物体动量的增加量，而与其他运动形态(比如内能Δε)是否出现无关，这就说明机械运动保持机械运动的形式是以动量来传递的．第二个式子表明当有其他运动形式出现时，动能的减少量等于其他形式能量的增量，即动能是以机械运动所具有的转变为一定量的其他形态的运动的能力来量度的机械运动．