行波的旋转矢量法和驻波的可视化*

周群益

(广州理工学院通识教育学院 广东 广州 510540)

肖桂英

(广州理工学院机电工程学院 广东 广州 510540)

王培颖

(广州理工学院通识教育学院 广东 广州 510540)

莫云飞

(长沙学院电子信息与电气工程学院 湖南 长沙 410022)

周丽丽

(赣南医学院医学信息工程学院 江西 赣州 341000)

旋转矢量法可以直观地描述简谐振动，但是并没有文献用于描述简谐波．驻波是两列振幅相等、频率相同、传播方向相反的简谐波叠加的结果．有文献用旋转矢量法研究驻波的特征[1～4]，虽然说明了一些问题，但是用旋转矢量法研究驻波较为困难，绘制的图像也不够具体形象．

有文献研究了驻波的能量[5～12]，推导了能量密度公式和能流密度公式，但是没有用图像说明问题．还有文献用MATLAB研究驻波的能量[13]，方法很好，若充分发挥MATLAB的可视化功能，则可进一步改进．

本文从简谐振动公式推导了简谐波的公式，用曲面说明简谐波的分布规律．用振动的旋转矢量法的动画说明了简谐波的传播过程，用动画的截图说明了驻波的形成过程，用曲面表示了能量和能流密度的分布规律，用动画的截图说明了能流的方向与能量分布之间的关系．

1 简谐振动和简谐波的旋转矢量法

1.1 波形曲面和曲线

如图1所示，设一个质点在原点做简谐振动，振幅为A，角速度为ω，初相为φ0．旋转矢量A顺时针旋转，ω的方向垂直纸面向里．

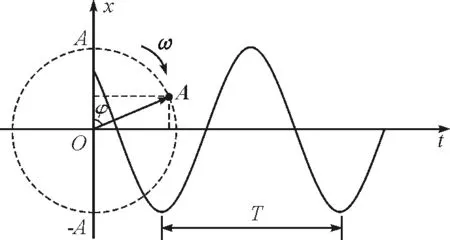
图1 简谐振动的旋转矢量图

经过时间t，相位φ=ωt+φ0，位移为

x=Acosφ=Acos(ωt+φ0)

(1)

这是质点的运动方程，其周期为

(2)

设波沿着Or方向传播，波速为u，则波长为

(3)

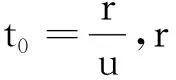
x=Acos[ω(t-t0)+φ0]=

(4)

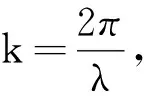
x(t,r)=Acos(ωt-kr+φ0)

(5)

用周期和波长可以表示为

(6)

此式便于画图．

取周期T为时间t的单位，取波长λ为坐标单位，取振幅A为位移单位，则无量纲的波动方程为

cos[2π(t*-r*)+φ0]

(7)

利用MATLAB的surf指令可画曲面，利用plot3指令可画三维曲线[14]．

如图2所示，取φ0=0，右行波的位移是波浪形的曲面．当r=0时，可得原点处质点的运动方程曲线，如实线所示；当t=0时，可得所有质点在初始时刻的波形曲线，如虚线所示．当r=2.5λ时，可得该处质点的运动方程曲线；当t=1.5T时，可得所有质点在该时刻的波形曲线．当r=2.5λ，t=1.5T时，质点的位移x=1A．

图2 波动方程曲面

1.2 波的传播的旋转矢量动画

利用MATLAB的计算和图形功能，我们设计了一个程序，可演示旋转矢量法与右行波传播的动画，见附录[14]．

执行程序，初始时刻的旋转矢量和波形曲线如图3所示，每一点的旋转矢量都在不同的tOx平行平面上，处于竖直或水平位置．

图3 初始时刻的各点的旋转矢量和波形曲线

按任意键(例如空格键或回车键)，旋转矢量和波形曲线如图4所示．所有矢量都旋转了一个角度，每一条矢量线与两条虚线组成一个直角三角形，矢量线在Ox轴上的投影就表示质点的位移，行波同时向右传播了一定的距离．波的传播方向与ω的方向相反．不断按任意键，各点的直角三角形随着矢量的旋转而改变，行波不断向右传播．当矢量旋转一周后，再按任意键，矢量就持续旋转，行波持续右行，直到按ESC键为止．

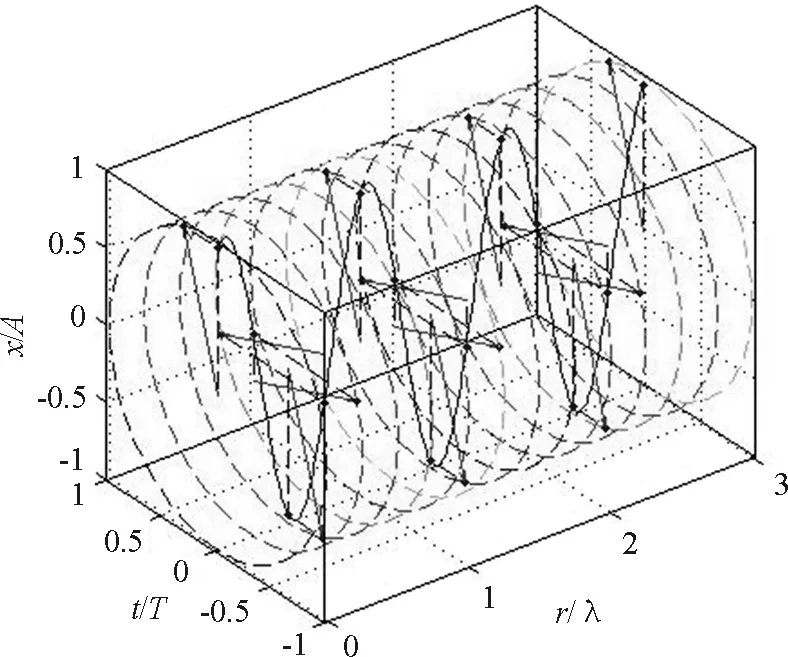
图4 某时刻各点的旋转矢量和波形曲线

修改程序也可以用旋转矢量法演示左行波的动画，读者不妨一试．

2 驻波的特点

2.1 驻波的位移

两列振幅相等、频率相同、传播方向相反的波的方程为(取初相φ0= 0)

x1(t,r) =Acos(ωt-kr)

(8)

x2(t,r) =Acos(ωt+kr)

(9)

其中，x1(t,r)是右行波，x2(t,r)是左行波．行波的特点是包含因子(ωt±kr)．两波叠加的结果为

x(t,r)=x1(t,r)+x2(t,r)=

2Acoskrcosωt

(10)

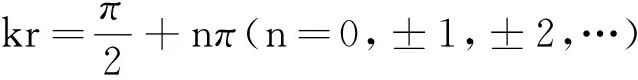
振幅为零，此处称为波节．除了波节之外，其他各点做简谐振动．当kr=nπ(n=0,±1,±2,…)时

振幅最大，即2A，此处称为波腹．其他点的振幅介于零到2A之间．

取周期T为时间t的单位，取波长λ为坐标单位，取振幅A为位移单位，则无量纲的行波方程为

(11)

(12)

利用MATLAB的动画功能，可演示左右行波传播的动画以及驻波形状变化的动画[14]．

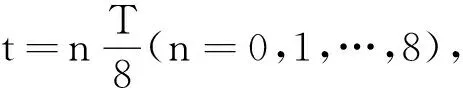
图5 右行波，左行波和驻波的截图

2.2 驻波的能量和能量密度

设媒质是弹性均匀媒质，其质量体密度为ρ，在位置r处取一个体积元ΔV，其质量Δm=ρΔV．质元的速度为

(13)

质元的动能为

(14)

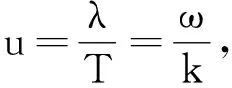
2ρA2ω2ΔVsin2krcos2ωt

(15)

对横波则要将杨氏模量Y改为切变模量G，结果完全相同．质元的机械能为

ΔE=ΔEk+ΔEp=

2ρA2ω2ΔV(cos2krsin2ωt+sin2krcos2ωt)

利用半角公式可得

ΔE=ρA2ω2ΔV(1-cos 2krcos 2ωt)

(16)

质元的动能、势量和机械能都是关于坐标和时间的二元函数，任何一个质元的能量都随时间做周期性的变化，其圆频率是驻波圆频率的2倍．由于能量公式中并不包括因子(ωt±kr)，所以能量并不随波传播．

在一个周期内，质元动能的平均值为

(17)

质元势能的平均值为

(18)

机械能的平均值为

(19)

可见，一个质元的动能和势能的平均值与坐标有关，平均动能大的质元，其平均势能一定小，但是机械能是常数．

在波节处，coskr=0，sinkr=±1，质元的动能为ΔEk=0，势能为

ΔEp=2ρA2ω2ΔVcos2ωt

(20)

这是因为在波节处的质元静止而相对形变会随着时间发生改变．

在波腹处，sinkr=0，coskr=±1，质元的势能为ΔEp=0，动能为

ΔEk=2ρA2ω2ΔVsin2ωt

(21)

这是因为在波腹处的质元不发生相对形变而速度随着时间发生改变．

单位体积内的能量称为能量密度，动能、势能和机械能的能量密度分别用wk，wp和w表示．机械能的能量密度为

(22)

能量密度也是关于坐标和时间的二元函数．在垂直于Or方向取一个截面S，在r处取一个体积元dV=Sdr，在波节与波腹之间的机械能为

(23)

可见，波节与波腹之间的机械能是恒定的，不随时间改变．

取周期T为时间单位，取波长λ为坐标单位，取最大能量ΔEm=2ρA2ω2ΔV为能量单位，就能将动能和势能无量纲化，两者之和就是无量纲的机械能，简称能量．

取最大能量密度wm=2ρA2ω2作为能量密度的单位，则无量纲的能量密度就等于无量纲的能量．

图6 驻波的动能和动能密度

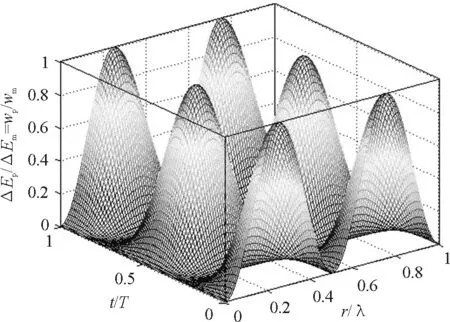
图7 驻波质元的势能和势能密度

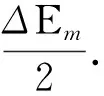
图8 驻波质元的机械能和机械能密度

2.3 驻波的能流密度

对于右行波来说，一个质元的动能与势能相等，可以证明其能量(机械能)为

ΔE1=ρA2ω2ΔVsin2(ωt-kr)

(24)

单位体积内的能量就是能量密度．因此，右行波的能量密度为

(25)

沿着波的传播方向单位时间内穿过单位面积的能量称为能流密度，其大小等于波速与能量密度之积．右行波的能流密度为

I1=uw1=uρA2ω2sin2(ωt-kr)

(26)

同理，左行波的能流密度为

I2=uw2=uρA2ω2sin2(ωt+kr)

(27)

驻波的能流密度为

I=I1-I2=

uρA2ω2[sin2(ωt-kr)-sin2(ωt+kr)]

利用平方差公式，展开上式再化简，可得

I=uρA2ω2sin 2krsin 2ωt

(28)

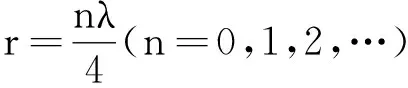
(29)

说明驻波并不传播能量．

取周期T为时间单位，取波长λ为坐标单位，取最大能流密度Im为能流密度单位，就能将右行波和左行波以及驻波的能流密度无量纲化．

利用左右行波和驻波完全相同的方法，可以演示3个能流密度的动画．

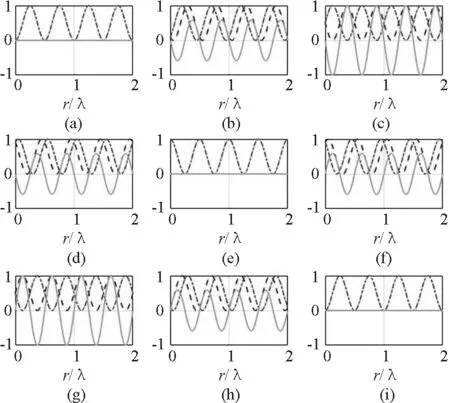
图9 右行波、左行波和驻波的能流密度截图

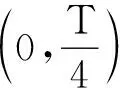
3 结束语

行波和驻波是机械波中的两个典型问题，波的传播和波形改变都可以用图形和动画表示．行波不但可以用曲面表示，还可以用旋转矢量法演示．在波节上质元的动能为零，势能随时间做周期性变化；在波腹上质元的势能为零，动能随时间做周期性变化．能量可以在相邻波节和波腹之间周期性流动，但不会传播．当能量向波节或波腹流动时，波节或波腹的能量就会增加，反之则减少．

学科交叉是学科发展的一个重要方向．MATLAB程序设计是一门学科，系统掌握这门知识有助于我们研究物理问题，也有助于物理教学．本文附录中的程序可供参考，相信有助于读者的教学和研究．