利用架空线测量接地阻抗时的互感问题分析

何智强，张 宣，严雅琳，潘卓洪，胡晓晖

(1.国网湖南省电力有限公司科技部，长沙 410007； 2.华北电力大学 河北省输变电设备安全防御重点实验室，河北 保定 071003； 3.武汉市康达电气有限公司,武汉 430070)

0 引言

大型和超大型的电站在电力系统中占有重要地位，对工作接地、防雷接地和保护接地的要求较为严格[1-3]。大型接地装置在设计、施工和维护等方面要耗费大量的人力和物力，尤其是接地测量时往往面临布线工作量过大和测量结果不准确的问题[4]，从而给接地装置正常工作和系统安全运行带来隐患。

DL/T 475《接地装置特性参数测量导则》中提到了利用架空线路做电流线和电位线测量超大型接地装置接地阻抗的有效性[5]：一方面，利用输电线路可极大减少大型接地装置接地测量时的布线工作量从而有效地加快测量进度；另一方面，利用电力线路的低阻特性可大大降低测量回路的阻抗，避免人工布线时电流引线截面积不足导致的电流回路阻抗过大的问题，从而有效提高测量的电流大小和信噪比。利用架空线测量接地阻抗还避免了人工放线的断线和触电风险，可有效减少巡线工作量。三峡电厂等超大型水利枢纽利用架空线测量接地阻抗取得了良好的应用效果[6]。使用架空线路作为电流线和电压线的情况下线路间的互感问题复杂，目前并没有有效的计算方法可供借鉴。

国内外学者一直致力于接地测量互感问题的研究。在三极法测量接地阻抗的基础上，解广润和方瑜等人提出在站址附近引入一个辅助电极来消除引线间互感，但该法需要满足较严格的条件，所以未见推广应用[7-8]。李汝彪等人用附加串联电阻法来消除互感影响，但该法会连带消去接地阻抗的电感分量，因而不适用于大型接地系统[9]。类似的，端木林楠等人提出了“双频-双路径电压线布置”的互感校正方法，由于需要拉大引线距离作二次测量，故容易受现场条件限制，布线工作量较大[10]。黄新波等人讨论了电压极选点对接地测量的影响，并列出了平行布线的互感计算公式[11]。马御棠等人提出了二次直线测量法消除互感，并通过了小地网的测试，但目前尚无法应用于大型接地系统的测量[12]。袁培等人在平行布线的情况下采用多次移动电压极的方式对电阻和电感分量进行拟合以消去互感分量，该法现场布线的工作量大，对仪器的测量精度要求也较高[13]。侯苏洋利用有限元方法仿真接地阻抗，利用公式法分析了平行布线引线间互感对接地阻抗测量结果的影响[14]。在上述文献的研究中，引线的地下镜像穿透深度计算公式参考了文献[8]的近似结果，但文献[8]也指出了更为准确的穿透深度计算公式，但目前未见文献[10-14]对此作出更正。Deri提出了更为准确的线路互感计算方法[15]，并在电力系统电磁暂态计算的线路模型中实现了应用[16]。

针对目前研究的不足，笔者提出了任意参数的架空线路零序互感模型，并实现了模型的复镜像算法求解。本研究方法在某500 kV大型接地装置的接地阻抗测量中实现了应用，并与其他互感计算方法进行了对比，验证了该方法的有效性。

1 架空线路的互感理论模型

任意布置的两直线l1和l2如图1所示，假设A和B分别为l1的起点和终点，E和F分别为l2的起点和终点，l1和l2间夹角为θ。直线GC为l1和l2的公垂线，A′和B′分别为A和B在l2上的投影，E′和F′分别为E和F在l1上的投影。

图1 任意布置的两直线导体模型示意图Fig.1 Schematic diagram of two linear conductor models with arbitrary arrangement

使用柱坐标系，假设角频率为ω，空气介电常数为ε，大地和空气的磁导率均为μ，大地介电常数为εe，大地电导率为σ，两引线间互感M为[17]

(1)

(2)

(3)

(4)

其中，z1和z2分别为dl1和dl2的z坐标，r1和r2分别为dl1和dl2的r坐标，r(r1,r2)表示D(dl1, dl2)在xy平面上的投影。

式(4)可用其泰勒级数的头三项来近似[15-16]：

(5)

工频情况下可以忽略位移电流的影响，式(5)可以简化为

(6)

式中，等号右侧第1项表示大地电阻率为零对互感的影响，第2项是大地电阻率不为零影响的主项，第3项为可微项。式(6)代入式(2)有

(7)

(8)

式(8)的结果简单，在0～100 kHz内具有较高的精度(一般情况下最大误差<10%)[16]。如果对精度要求更高，公式(4)可采用复镜像法来进行求解[18-19]：

(9)

公式(9)代入(4)，由李普希兹积分有[8]：

(10)

把复镜像形式(10)代入互感计算公式(1)有

(11)

(12)

(13)

(14)

真空中引线l1和l2间的互感M的表达式如下：

(15)

可以看出，互感计算的关键在于求取下式的二重积分：

(16)

对图1所示的两任意放置的棒导体的H解析公式为：

(17)

(18)

式中，不带尖括号的变量表示两点间距离，恒为正，带尖括号的变量在其方向与AB或EF方向一致时为两点间距离，否则为取负的距离。

无论是式(7)还是式(9)，地下的回流镜像的位置是复数，而式(17)和式(18)是Heppe方法是针对实镜像的推导结果，考虑式(4)的复镜像后，带电的导体会被移动到不同的复镜像位置并最后完成加权，如式(14)所示。式(9)中的复镜像位置β代入式(17)和式(18)就可以实现Heppe方法在复数域上的延拓。假设l1为源导体，l2为场导体，处理复镜像法时，l2参数不变，l1原来位置沿z轴从下移2z1+β，再代入式(17)和式(18)进行求解。明显地，C、E′和F′位置也需要相应下移2z1+β以满足复镜像法的使用，而其余点的位置则不需要改变，θ、Ω和尖括号的变量也没有改变。涉及复数位置的C、E′和F′点的变量求距离需要采用复向量求模的运算方式来进行求解。明确了上述的运算规则以后就完成了基于复镜像延拓的Heppe方法推导。

式(17)的情况比较复杂，在两直线相互平行时可以得到一个简化的结果。如图2所示，置l1在x轴上，l1起点与坐标原点重合，l2平行于l1，H的解析公式为

图2 两平行直线导体模型示意图Fig.2 Schematic diagram of two parallel linear conductor models

(19)

其中：L1和L2分别是l1和l2的长度；(x，y，z)是l2起点的坐标；d为l1和l2之间的距离。考虑复镜像的位置后，式(19)直接按原像z位置下移2z1+β来更新d即可完成求解。

另外，l1和l2相互垂直时因为cosθ=0导致互感为0，故在此不再列举垂直情况下H的表达式。

2 测量案例

选取某500 kV大型水电站(接地装置对角线长度约为2.5 km)，利用其两条500 kV架空线线路测量接地阻抗，具体的线路走向示意图见图3，粗实线路表示电流线，细实线路表示电压线。线路各级杆塔的经纬度坐标见表1和表2，末端杆塔的经纬度坐标近似地作为电流极和电压极的位置。测量时断开了所有测量线路的避雷线以避免其对测量结果的影响。两线路的末端杆塔见图4。

图3 电压、电流线路的位置示意图Fig.3 Location diagram of voltage and current lines

图4 电压极和电流极的杆塔Fig.4 Location diagram of voltage and current lines

表1 电流线路的杆塔经纬度坐标Table 1 Longitude and latitude coordinates of tower of current line

表2 电压线路的杆塔经纬度坐标Table 2 Tower longitude and latitude coordinates of voltage line

根据地球经纬度与距离的关系，点(x1,y1)与点(x2,y2)之间的南北向距LN为

(20)

其中θ= (y1+y2) π / 360，赤道半径a=6 378.137 km，离心率e2= 0.006 694 38。同理，东西距离Dx为

(21)

点(x1,y1)与点(x2,y2)之间的距离D为

(22)

表1和表2中，C2～C5和P2～P5的数据相同表示两条线路在过江段使用同塔双回形式，电压/电流线路其余杆塔均为直立塔。电压线路的电流引线选用线路的C相，过江段高度43 m，直立塔段高度23 m；电压线路的电流引线选用线路的A相，电流线路过江段高度66 m，直立塔段高度23 m；直立塔段中，电压线/电流线距离杆塔中心线8 m，两者为最大距离的布置形式(见图4)；电压线与电流线在过江段的水平距离为20 m。测量段内两线路均不换相。

计算不同大地电阻率情况下的线路互感，结果见表3。

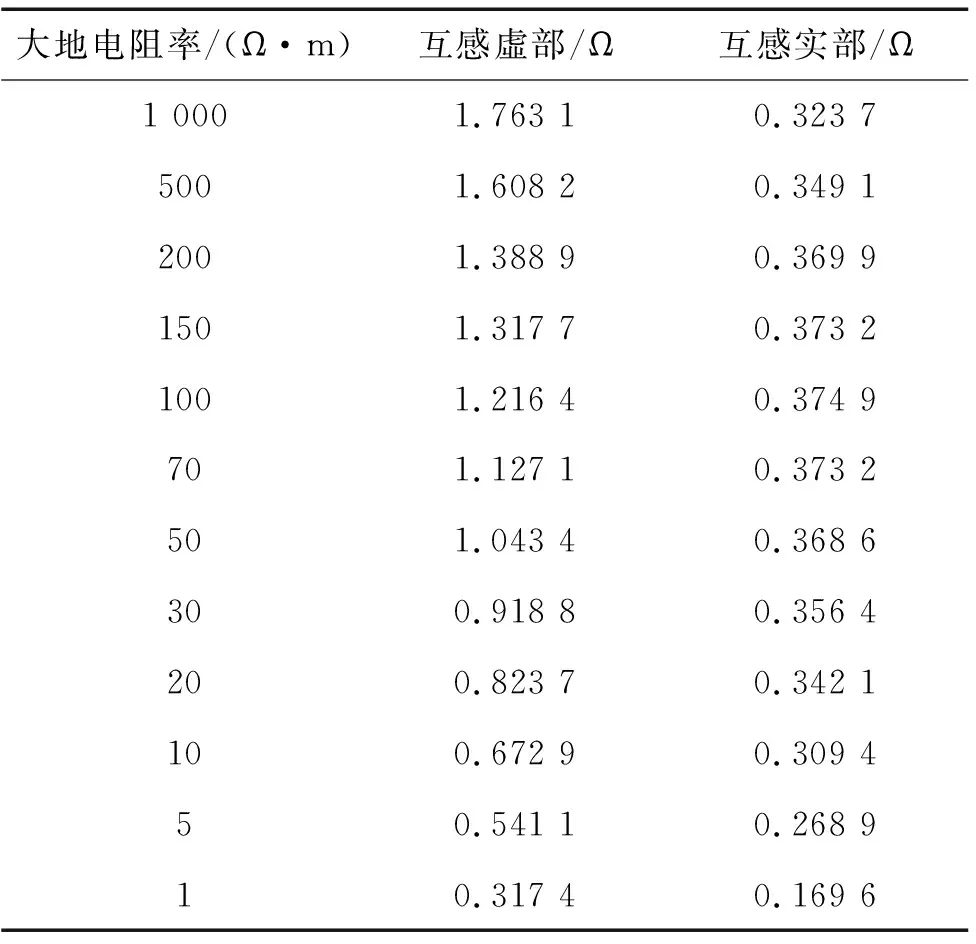
表3 线路互感的计算结果(50 Hz)Table 3 Calculation results of line mutual inductance (50 Hz)

从表3的计算结果可以看出，随着大地电阻率的减少，互感虚部呈现一直减小的趋势。由于复穿透深度正比于土壤电导率的开方，电阻率的减少带来穿透深度的减少，所以地下回流电流对电压线上形成的抵消影响更大，故互感的虚部随电阻率减少而减少。互感实部的形成原因相对复杂：由于大地是不良导电介质，测量电流在大地中回流时会形成一个滞后于互感的损耗量，即电阻分量。在测量线路较长的情况下，互感的电阻分量与接地电阻数量级一致，这是必须引起注意的，所以使用线路测量接地阻抗时必须扣除其影响。表3的计算结果中，由于复穿透深度的变化，以及它和大地电阻率的配合关系，使用地中电流的断面电阻不再是单调变化，互感的电阻分量呈现随电阻率增加先增加而后减少的趋势。表3的计算结果还表明：土壤电阻率为100 Ω·m时达到峰值(约为0.375 Ω左右)。

输电线路导线和避雷线间互感问题是过电压研究中的重点问题，目前已经非常完善。然而在利用输电线路进行接地阻抗测量时，由于线路不再是平行的情况，所以需要使用Heppe公式。另外，过电压的计算软件只考虑同档距下相导线和避雷线之间的耦合，忽略不同档距线路的电磁耦合会导致互感的评估结果偏小。

为了对比不同穿透深度计算方案下线路之间的互感，在工频情况下取大地电阻率100 Ω·m，线路互感的计算结果见表4。不同穿透深度计算公式如下：

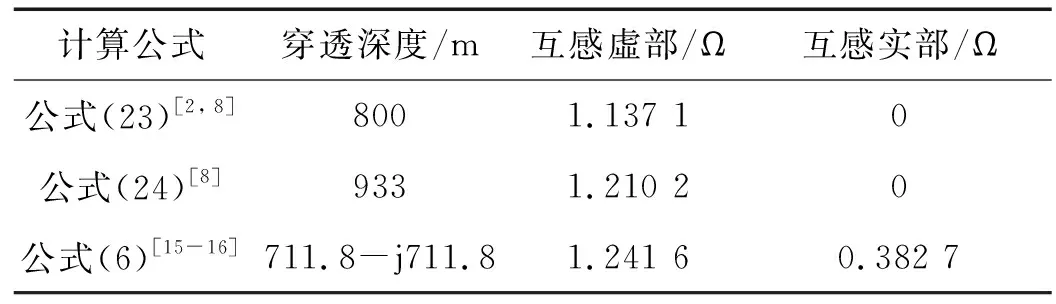
表4 不同穿透深度情况下的线路互感计算结果(工频，大地电阻率取100 Ω·m)Table 4 Results of mutual inductance under different penetration depth (50 Hz, earth resistivity is set to 100 Ω·m)

(23)

(24)

从计算结果可以看出，式(23)和(24)的互感虛部结果偏小，而互感实部为0。式(23)采用的理论模型比较粗略，线路藏于挖空的地表，所以穿透深度偏小，互感的结果也偏小。式(24)是模型相对严格一些，但无法评估互感实部。故式(23)和(24)是无法准确评估线路测量接地阻抗时的互感的。公式(6)已经比较接近论文方法的结果。式(6)存在大小为负值的可微项，故评估结果会略大，但误差在5%以内，故可以作为工程评估手段。论文方法是严格准确的方法，可作为线路测量接地阻抗时校正引线间互感的有效方法。

采用异频法进行接地阻抗的测量，测量结果折算至工频为0.425+j1.251 Ω，电站的分流系数实测值为41.33%。经调研，当地大地电阻率约为100 Ω·m，故去除线路互感情况下的电站接地阻抗实部R和虚部X分别为

(25)

(26)

故经过校正后电站的接地阻抗大小为0.151 Ω，阻抗角为33.57°。该结果与电站的设计值0.16∠28.30° Ω比较一致，略小于6年之前电站投运时夹角法的接地阻抗测量值0.18 Ω。

3 结论

论文研究了使用架空输电线路测量接地阻抗时的互感评估方法，所得结论如下：

1)推导了任意位置线路零序互感的理论模型，并实现了模型的复镜像算法求解，有效提高了模型求解的准确性。本研究成果为架空线测量接地阻抗的实践与评估提供有效参考。

2)运用某大型500 kV电站的实测案例验证了方法的有效性，并分析了不同穿透深度公式情况下的线路互感。结果表明大地电阻率会令线路互感角度小于90°，在使用线路进行接地测量时必须注意扣除其影响。