一种太阳能集热器流体平均温度计算方法
2022-07-04徐立孙飞虎李志张强强
徐立,孙飞虎,李志,张强强,3*
(1.中国科学院太阳能热利用及光伏系统重点实验室,北京市 海淀区 100190;2.中国科学院电工研究所,北京市 海淀区 100190;3.中国科学院大学,北京市海淀区 100049;4.北京市太阳能热发电工程技术研究中心,北京市 海淀区 100190)
0 引言
太阳能热发电技术近年来受到广泛关注[1-4]。我国能源局在2018年立项20个太阳能热发电示范项目,包含塔式、槽式和碟式等多种热发电技术形式,其中塔式发电技术占一半以上。
目前,已有很多学者[5-18]对太阳能集热器进行了研究。文献[8]将Monte Carlo方法和Gebhart方法耦合起来,提高了太阳能集热器模型边界条件的准确性。文献[9]提出了适用于太阳能集热器设计的性能模型,并与Gemasolar电站的数据进行了比对。文献[10]给出了一种快速计算太阳能集热器出口温度的模型。文献[11-12]提出了一种新的套管式太阳能集热器结构,二维仿真分析结果显示,如果只需要计算出口温度及太阳能集热器的效率,则周向的温度变化可以忽略。文献[13-14]采用Monte Carlo方法计算太阳能集热器的辐射换热,同时采用FLUENT计算太阳能集热器的对流换热,两者耦合可以较为准确地计算太阳能集热器的热性能。文献[15]分开考虑辐射换热和对流换热,在辐射换热计算中使用Monte Carlo方法得到太阳能集热器微元表面之间的角系数,在对流换热计算中使用FLUENT判断对流的类型,但是并没有得出一个综合表征热损失的参数。文献[16]使用Gebhart和Clausing方法分别计算太阳能集热器的辐射热损失和对流热损失,由于该辐射换热计算过程过于复杂,所以并没有将其与对流换热耦合在一起。文献[17]对二维开口腔体的自然对流换热和壁面辐射换热情况进行了数值模拟。文献[18]建立了太阳能热发电站的模型,用于预测其长期性能,在建模过程中测试了节点数量对太阳能集热器效率的影响,研究结果显示,在流体物性不变的前提下,每个管板可以使用单个节点替代。
以上文献大多先把太阳能集热器离散为多个微元,然后采用Monte Carlo方法计算太阳能集热器的辐射换热或者角系数;在对流换热的计算上通常使用经验公式或FLUENT;大多分开考虑辐射和对流热损失,而没有提出可以考虑各种热损失的综合性参数。
为此,本文提出使用热损失系数来综合表征太阳能集热器的辐射和对流热损失,并代入能量平衡方程计算太阳能集热器的输出能量。该能量平衡方程需要用到太阳能集热器的流体平均温度,由于平均温度无法通过准确测量得到,因此本文通过推导使用入口温度替代平均温度。经过上述处理后,本文方法可以快速预测太阳能集热器的长期热性能。
1 数学模型
太阳能集热器稳态工况下的输出功率表示为

式中:Qnet,in为太阳能集热器的净入射功率或输入功率,即单位时间入射能量与反射能量损失之差;Ap为集热器面积;Tf为流体平均温度;Ta为环境温度;F′和UL分别为集热器的效率因子和总热损失系数[19]。与其他方法不同,UL可以直接用于比较不同太阳能集热器的热损失情况。
式(1)可以用于预测太阳能集热器的长期性能,然而流体平均温度Tf不容易得到,因此有必要提出一种计算流体平均温度的方法。
太阳能集热器结构如图1所示。太阳能集热器由管板组成,管板结构如图2所示。各管板的吸热管排布在一起组成了吸热面,因此可以把管板视为太阳能集热器的基本组成单元。将管板从入口至出口方向依次编号为1,2,…,N,流体的平均温度也可以表示为各管板中流体温度的加权平均数,即


图1 太阳能集热器结构示意图Fig.1 Structure of solar collector
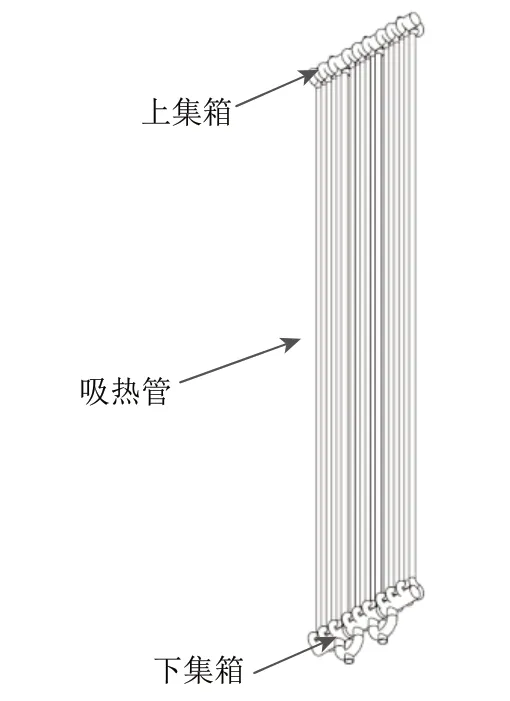
图2 管板结构示意图Fig.2 Structure of receiver panel
式中:Tf,i为管板i的流体平均温度;χi为加权系数,定义为
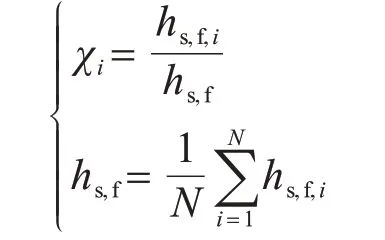
式中:hs,f,i为管板i的对流换热系数;hs,f为所有管板的平均对流换热系数。
联立方程(1)和(2)并修正环境温度可得

式中:As,f,i为管板i的换热面积;FL为中间变量,定义为
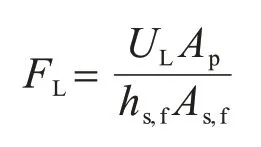
其中As,f为总的换热面积。
忽略各管板连接管路的热损失,将方程(3)应用管板i(i>1),并与流体吸收的能量平衡方程联立,可得

式中:Tfi,1为太阳能集热器的入口温度;βa和βm为中间变量,

式中:ṁ为质量流量;Cf为流体比热。
将所有管板的平均温度表达式累加,可得整个太阳能集热器的流体平均温度为
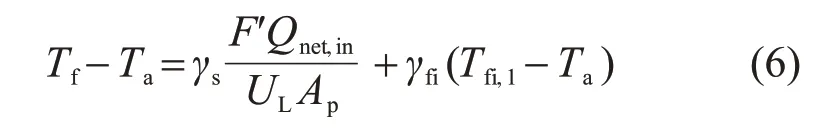
式中γs和γfi为中间变量,

太阳能集热器的入口温度在实验中很容易测量得到,也是各种仿真模型的输入参数,因此使用入口温度替代流体平均温度更加实用。方程(6)只适用于单个入口和出口的太阳能集热器,对于多进出口的太阳能集热器需要重新进行推导。
2 实验装置及计算条件
图3是实验平台的结构图,其中太阳能集热器由7个管板并联组成,吸热面由多根不锈钢吸热管的表面组成。每个管板设有3个温度测点,用于监测管板的壁面温度。

图3 实验台结构图Fig.3 Structure of experimental platform
该集热器使用电能作为能量输入,每个管板作为电阻由于焦耳效应而产生热量。与室外工作的太阳能集热器不同,该集热器无需考虑反射能量损失。由于各管板的电阻相同,每个管板的输入能量也相同。
实验中采用了中山大学自行研制的新型熔融盐,其主要成分为质量分数53%的KNO3、40%的NaNO2、7%的NaNO3以及5%的添加剂,流体的密度ρ、黏度μ和导热系数k关系式[20]如下:

该熔融盐的熔点为142℃,液态的比热基本恒定为1 561.7 J/(kg·K)。表1为太阳能集热器的结构参数[21-22]。

表1 太阳能集热器的结构参数Tab.1 Structural parameters of solar collector
利用方程(6)来计算该太阳能集热器的流体平均温度,通过将计算结果与实验数据进行对比来验证方程的正确性。为了分析包含能量分布在内的参数对太阳能集热器热效率的影响,定义一个参考工况,当研究单个参数对太阳能集热器效率的影响时,其他参数保持与参考工况一致。参考工况中各参数的值如表2所示。

表2 参考工况下各参数的值Tab.2 Parameter values under reference condition
表2中后4个参数vw、εp、εr、kp仅用于计算总热损失系数UL,并不直接影响Tf和Qabs,因此,参数分析侧重于表2中前4个参数。
实验过程中,太阳能集热器的输入能量和流量可以通过调整输入电流及变频进行调节。因此,该实验平台可以进行多工况的实验。测量参数的范围及不确定度如表3所示。

表3 测量参数的范围及不确定度Tab.3 Ranges and uncertainties of test parameters
3 结果与讨论
以某次实验为例,在该实验开始后迅速将输入功率提升至73.39 kW,实验过程中保持流量恒定为0.24 kg/s。图4是实验过程中太阳能集热器的入口温度和输入功率,图5是实验过程中的环境温度及流量。将上述实验数据代入方程(6),计算实验过程中太阳能集热器的流体平均温度,其计算结果与实验数据的对比如图6所示。

图4 太阳能集热器的入口温度和输入功率Fig.4 Inlet temperature and input power of solar collector
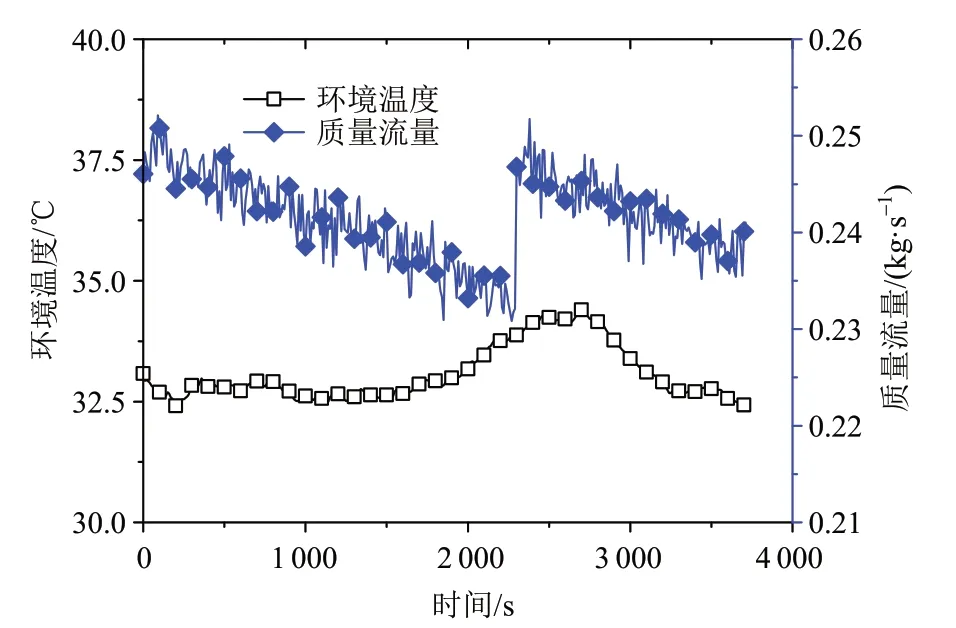
图5 太阳能集热器的环境温度和质量流量Fig.5 Ambient temperature and mass flow rate of solar collector

图6 流体平均温度的计算结果与实验数据的对比Fig.6 Comparison between calculation results and experimental data of average fluid temperature
图6将实验过程分为2个阶段,在P1阶段,由于输入功率迅速升高,实验数据也从初值开始迅速增大,然而计算结果在该阶段基本保持恒定,两者的相对误差超过15%;在P2阶段,实验数据由于入口温度的缓慢上升而升高,计算结果与实验数据的相对误差减小到3%以下。之所以2个阶段有如此的差异,是因为在方程(6)的推导过程中,最重要的假设就是太阳能集热器处于稳态工况下运行。因此,太阳能集热器的工作状态越接近于稳态,计算结果也就越准确。在实际工作中,太阳能集热器经常在多云等变辐照气象条件下运行,运行工况无法保持稳态,因此方程(6)无法用于计算太阳能集热器的秒级或者分钟级短期动态特性。在评估较长时间跨度(如5~10 a甚至更长时间)下太阳能集热器的性能时,辐照、风速等外界条件一般取为小时平均值或者日平均值,此时适宜采用稳态能量平衡方程进行性能的核算。因此,方程(6)可以用于预测太阳能集热器的长期性能。
由于实验平台只包含一个熔盐储罐,太阳能集热器的入口温度无法保持恒定,因此实验平台不能进行稳态试验工况测试。为了使实验工况满足验证方程(6)的条件,定义太阳能集热器的进出口温差在1 min内波动小于0.2℃时为相对稳态。图7为在不同输入功率和流量下太阳能集热器的流体平均温度的计算结果与实验数据的相对误差,对比所用数据点都处于相对稳态。
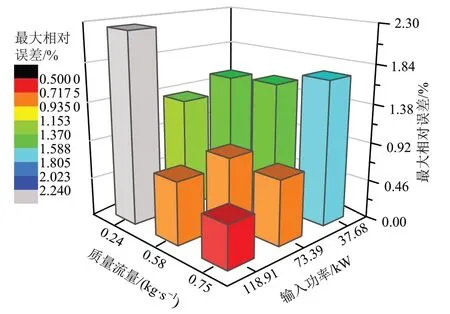
图7 不同工况下流体平均温度的计算结果与实验数据的最大相对误差Fig.7 Maximum relative error between calculation results and experimental data of average fluid temperature under different working conditions
从图7可以看出,在最小质量流量和最大输入功率组合的工况下,流体平均温度出现了最大相对误差;而当最大质量流量与最大输入功率组合在一起时,流体平均温度的相对误差最小,整体上并无规律。9种工况下,流体平均温度的最大相对误差为2.24%。因此,本文中的模型可以准确计算相对稳态下的太阳能集热器流体平均温度。相对误差可能由如下因素导致:1)每个管板只有3个温度测点,即太阳能集热器共有21个温度测点,因此测点数量不足会导致所测壁面平均温度与真实值有差别;2)太阳能集热器的管内换热情况采用经验公式进行计算,得到的对流换热系数与真实值之间也会有差别。
在推导流体平均温度表达式时,输入功率的空间分布也被考虑在内。图8是输入功率的6种分布情况,图9是6种功率分布情况下太阳能集热器的效率值。由于本文中太阳能集热器采用电能作为能量输入,因此在计算太阳能集热器效率时不考虑反射能量损失:


图8 太阳能集热器输入功率的分布Fig.8 Distribution of input power of solar collector
从图9可以看出,分布1—4对太阳能集热器效率几乎没有影响,分布5下太阳能集热器的效率最高,分布6下太阳能集热器的效率最低。管板是从太阳能集热器的入口到出口方向进行编号,因此,分布5中输入功率随着流体流动升温而逐渐增大,这种分布可以降低壁面与流体间的温差,因此可以改善换热效果。分布6则跟分布5刚好相反,其输入功率随着流体流动升温而逐渐减小,这种分布会导致壁面和流体间的温差较大,从而降低了换热效果及太阳能集热器的效率。

图9 不同输入功率分布下太阳能集热器的效率值Fig.9 Thermal efficiency of solar collector under different input power distributions
图10展示了入口温度及环境温度对太阳能集热器效率的影响。可以看出,太阳能集热器的效率正比于环境温度,环境温度升高有利于减小太阳能集热器的热损失,从而增大太阳能集热器的效率;入口温度升高实际上提升了流体的温度,从方程(1)可知,流体温度越高,热损失越大,从而效率越低。与环境温度相比,入口温度对效率的影响较大,但是由于太阳能集热器的采光口较小,导致太阳能集热器的热损失也较小,因而从绝对数值上来看,两者对太阳能集热器效率的影响都较小。

图10 入口温度与环境温度对太阳能集热器效率的影响Fig.10 Effect of inlet and ambient temperature on thermal efficiency of solar collector
图11为输入功率和流量对太阳能集热器效率的影响。可以看出,当流量恒定时,初期输入功率增大会提高太阳能集热器的效率,但是当输入功率超过某点后,太阳能集热器的效率会随着输入功率的增大开始降低。图11中的灰色点即为太阳能集热器在恒定流量下对应的最大效率值。当输入功率恒定时,增大流量可以显著地提高太阳能集热器的效率。然而,当流量已经足够大时,继续增大流量对太阳能集热器效率的提高作用会越来越小。

图11 输入功率与流量对太阳能集热器效率的影响Fig.11 Effect of input power and mass flow rate on thermal efficiency of solar collector
采用敏感性分析[23]找出对太阳能集热器效率影响较大的因素。图12为不同参数对太阳能集热器效率的敏感性分析结果,可以看出,在分析范围内,太阳能集热器效率与流量、环境温度成正比,与入口温度成反比。在归一化数值0.5~1.0范围内,太阳能集热器效率与输入功率成正比;在归一化数值大于1.0后,太阳能集热器效率与输入功率成反比。在归一化数值0.5~1.0范围内,流量对太阳能集热器效率的影响最大;在归一化数值0.7~1.3范围内,入口温度对太阳能集热器效率的影响也较大;流量变大后对太阳能集热器效率的影响变小,该结论与图11的分析一致。
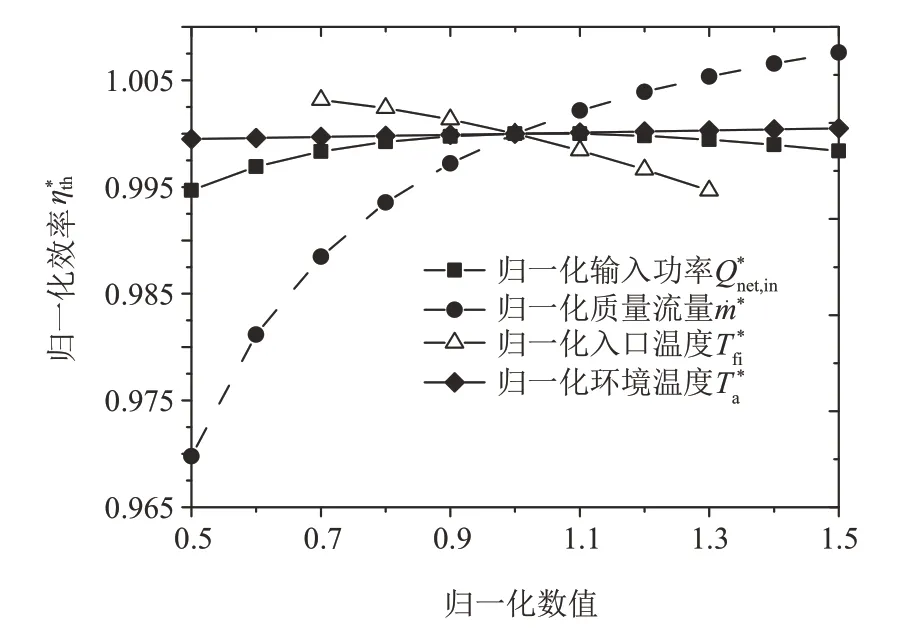
图12 不同参数对太阳能集热器效率的敏感性分析Fig.12 Sensitivity analysis of different parameters on thermal efficiency
4 结论
基于太阳能集热器的基本组成单元管板提出了一种计算流体平均温度的方法,并用9种实验工况的数据对该方法进行了验证。对比结果显示,该方法可以准确地计算太阳能集热器在稳态下的流体平均温度。分析了不同输入功率分布下太阳能集热器的效率情况,研究了不同参数对太阳能集热器热效率的影响,具体结论如下:
1)输入功率随流体流动方向逐渐增大的分布有利于提高太阳能集热器的效率,反之则会降低太阳能集热器的效率,其余分布对太阳能集热器的效率影响不明显。
2)当输入功率恒定时,增大流量可以有效提高太阳能集热器的效率,但是当流量增大到一定数值时,继续增大流量对提高太阳能集热器效率的作用将减小;当流量恒定时,太阳能集热器效率随着输入功率的增加会先升高后降低;太阳能集热器的效率与入口温度成反比,与环境温度成正比。
需要注意的是,该方法基于稳态假设,不能用于计算太阳能集热器在短期动态过程的性能。
