一种功能可配置的可逆触发器设计
2022-07-02王伦耀储著飞夏银水
吴 钰,王伦耀,储著飞,夏银水
(宁波大学信息科学与工程学院,浙江宁波 315211)
1 引言
能耗问题目前已成为制约集成电路发展的一个重要因素.Landauer 指出,能耗来源于现有逻辑电路的不可逆操作,降低电路功耗的关键是将不可逆操作改造为可逆操作[1]. 因此,可逆逻辑设计成为低功耗设计的一种途径;同时,可逆逻辑在量子技术、低功耗设计、信息安全等其他科学领域有着重要的作用[2~5].
可逆逻辑电路包括可逆组合逻辑电路和可逆时序逻辑电路,并可以由具有不同逻辑功能的基本可逆逻辑门连接构成[6~8]. 可逆触发器是构成可逆时序电路的基本单元,目前在可逆触发器设计中主要采取2 种方法. 第一种是结构替代方法. 该方法在非可逆触发器电路基础上,用可逆逻辑门替代构成非可逆触发器中的逻辑门,进而得到可逆触发器[9,10]. 用替代的方法实现可逆触发器设计简单易行,但得到的电路往往结构复杂,量子代价(Quantum Cost,QC)[11]高. 另一种是根据触发器工作原理,先提出可逆Latch,进而提出可逆电平触发器和边沿触发器[12~14].
本文主要讨论可逆边沿触发器设计. 不同于文献[9,10,12~14]的设计方法,本文在分析D,T 和JK 触发器次态方程的基础上,提出了上述3种触发器次态方程的统一表达式,并在可逆Latch 的基础上,分别提出了逻辑功能可配置的可逆电平触发器和可逆边沿触发器电路. 本文通过设置特定输入,使得提出的电路结构分别具有可逆D,T和JK触发器功能;同时,在提出的单边沿逻辑功能可配置的可逆触发器基础上提出了逻辑功能可配置的双边沿触发器设计. 另外,不同于已有可逆触发器,本文逻辑功能可配置的可逆触发器具有异步置数功能,有利于实现可逆时序电路初始化.
2 基本可逆逻辑门
可逆逻辑电路由基本可逆逻辑门组成,构成本文可逆触发器电路的可逆逻辑门为Feynman 门、Fred⁃kin门[15].
图1 为Feynman 门(也称FG 门)的电路符号和逻辑功能.x为控制位输入,y为目标位输入,y′为目标位输出,且存在

图1 Feynamn门

式(1)中,符号“⊕”表示逻辑“异或”运算. 通过预置x,y的值,使得y′可以等于xˉ,yˉ,x或y. 另外,当y=0 时,y′=0⊕x=x,即目标位输出等于控制位输入,本文把这种情况称为对控制位的复制.
图2 为Fredkin 门(也称F 门)的电路符号和逻辑功能.x为控制位输入,y和z为2个目标位输入. 它们对应的输出为

图2 Fredkin门
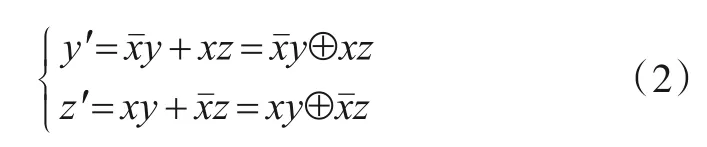
由式(2)可得,当x=1 时,y′=z,z′=y,即F 门的输出为输入的交换,y被分配到输出端z′;当x=0 时,y′=y,z′=z,F 门的输出为对应的输入,y被分配到输出端y′.因此,F 门具有数据分配功能. 另外,也可以通过预置y和z的值,实现输出为控制位x的取反.
3 可逆电平触发器设计
3.1 具有存储功能的可逆电路
Latch 是构成触发器电路的基本结构. 图3 为用F门和FG 门构成的可逆Latch 结构. 控制信号为C,Q_n和Q1为F门的输入,Q和g为F门的输出,其中g为垃圾位输出. FG 门的控制信号为Q,目标位输入为0,目标位输出为Q1.

图3 可逆Latch电路结构
由式(1)和式(2)可得,输出Q可以用式(3)来描述,即
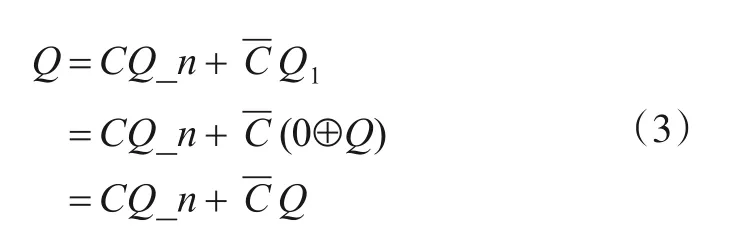
当C=0时,式(3)蜕化为恒等式Q=Q,即实现数据锁存. 而从图3 可得,当C=0 时,FG 门处于复制状态,输出Q被复制到F 门的其中一个输入端,F 门处于非交换状态,即Q=Q. 当C=1 时,式(3)变成Q=Q_n,实现输出数据的更新.
3.2 可逆电平触发器设计
电平触发器的特点是在控制信号高电平(或低电平)时处于信号接收状态,而在控制信号低电平(或高电平)时实现对已接收信号的锁存. 现假设控制信号为C,C也是时钟信号,Q+为可逆电平触发器的次态,Q为现态,则低电平锁存的可逆电平触发器的次态方程可以用式(4)来表示,即

式(4)中Q_n为次态值.Q_n由可逆触发器的现态和输入决定. 不同的Q_n表达式对应不同的触发器. 比较式(4)和式(3)可得,二者具有相同的表示形式,因此电平触发器可以在图3 电路基础上加上实现Q_n的电路就可得到具有不同逻辑功能的电平触发器.
D触发器的Q_n可以表示为

T触发器的Q_n可以表示为

JK触发器的Q_n可以表示为

式(5)~(7)具有共同的表达式形式,可以进一步表示成式(8)的形式:

式(8)中I1和I2为2 个输入变量,s为变量极性控制信号. 当I1=I2=D,且s=0 时,式(8)变成式(5),实现D触发器功能;同理,当I1=I2=T,且s=1 时,式(8)变成式(6),实现T 触发器功能;当I1=J,I2=K,且s=1时,式(8)变成式(7),实现JK触发器功能.
将式(8)代入式(4),得到可逆电平触发器逻辑功能的描述,即

由上述分析可知,通过设定I1,I2和s的取值可以使图4电路实现D,T和JK触发器功能,因此称图4电路为功能可配置的可逆电平触发器.
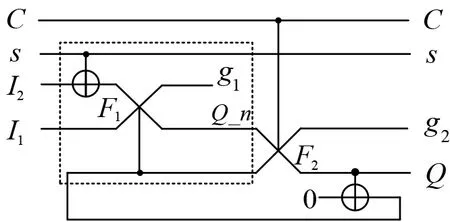
图4 功能可配置的可逆电平触发器
表1中给出了在不同现态和输入时,图4中Q_n的取值. 表1中标有“X”的地方表示在对应的输入和现态下,Q_n处于不稳定状态. 以表1 中Q=0,I1I2=11,s=1 为例,此时图4触发器输出将处于一直翻转的不稳定状态.为使图4电路具有稳定的输出,需要对其输入进行约束.

表1 C=1时图4电路Q_n取值情况
考虑到s=0 时,对应的是D 触发器功能,且要求I1=I2=D,因此表1 中带有“*”的X 对应的输入组合是不可能出现的,可以不用考虑. 因此图4 电路的输入必须满足

4 可逆边沿触发器设计
在非可逆触发器设计中,触发器的触发方式是由电路的结构形式决定的,那些采用2个电平D 触发器结构组成的触发器,无论其逻辑功能如何,一定是边沿触发的. 非可逆边沿触发器的设计思想同样也可以用于可逆边沿触发器设计.
图5 为提出的功能可配置可逆边沿触发器电路.其电路结构是在图4电路基础上,通过插入由F3和FG3构成的Latch,实现边沿触发. 图5 中包含了2 个Latch.一个由F2和FG2构成,简称为L1;另一个由F3和FG3构成,简称为L2.

图5 功能可配置的可逆边沿触发器
当C=1时,L1处于锁存状态,并将锁存的数据从Q端输出,同时L2处于接收数据状态,接收的数据为Q_n. 当C由1 变到0 即时钟下降沿时,L2处于锁存状态,锁存的数据就是时钟下降沿时Q_n的值,同时L1处于接收数据状态,L1接受的数据来自L2锁存的数据,并从Q端输出. 因此,图5电路具有下降沿触发的特性.
图5 可通过配置s,I1和I2的值,使得Q_n的表达式与D,T 和JK 触发器的逻辑功能描述一致,进而实现边沿D,T和JK触发器的功能.
在时序电路设计中一般要求电路具有异步状态预置功能,以实现时序电路初始化的目的,这就要求触发器具有异步置“1”或置“0”的功能.
图6 为本文提出的具有异步置“1”或置“0”功能的可逆边沿触发器电路. 图6电路结构是在图5电路基础上,增加了异步置数信号M和预置数A输入端,同时也增加了可逆门F0和F4.

图6 具有异步置数功能的可配置可逆边沿触发器
图6 电路中,当M=0 时,F0,F4处于非交换状态,因此F2,F3的控制位为C,同时预置数A从g4输出,对后面电路没有影响. 因此在M=0时,图6电路与图5电路的逻辑功能是等效的.
当M=1 时,F0,F4处于交换状态,因此,无论C为何值,F2,F3因控制位信号始终为逻辑“0”,处于非交换状态,从而使得预置数A可以直接输出到Q端. 同时,当M=1 时,由F3和FG3构成的Latch 处于锁存状态,锁存的数据为预置数A;而由F2和FG2构成的Latch 处于接受数据状态,接受的数据为预置数A. 因此,在M=1时,不管信号C,s,I1和I2如何变化,输出Q均等于预置数A.
当M从1 变成0 时,若C=1,则由F2和FG2构成的Latch 处于锁存状态,锁存的数据为预置数A,输出Q为A;若C=0,F3和FG3构成的Latch 处于锁存状态,锁存的数据为预置数A,而由F2和FG2构成的Latch 处于接受数据状态,接受的数据为锁存在F3和FG3构成的Latch的预置数A,输出Q也为A. 即在M失效后,触发时钟有效沿到来之前,输出端保持预置数A不变. 由此可得,在图6电路中,不论C为何值,当M为高电平时可以实现异步置数,预置数为A.
5 可逆双边沿触发器设计
在非可逆双边沿触发器电路设计中,存在2 个Latch 总是交替处于锁存和接受数据状态,而数据选择器总是选择处于锁存状态的数据加以输出,从而实现双边沿触发器的功能. 非可逆双边沿触发器的设计思想同样也可以用于可逆双边沿触发器的设计.
图7 为提出的功能可配置的可逆双边沿触发器电路. 其电路结构是在图5 电路基础上,增加了一个与L2并行的L3,同时为了实现在不同时钟电平下将Q_n分配到L2和L3中,又增加了F5. 在图7 中,当C=0 时,L3处于接收数据状态,接收的数据为Q_n,L2处于锁存状态,锁存的数据就是时钟下降沿时Q_n的值,并从Q端输出;当C=1 时,L2处于接收数据状态,接收的数据为Q_n,L3处于锁存状态,锁存的数据就是时钟上升沿时Q_n的值,并从Q端输出. 因此,图7电路具有双边沿触发的特性. 图7 可通过配置s,I1和I2的值,使得Q_n的表达式与D,T 和JK 触发器的逻辑功能描述一致,进而实现双边沿D,T和JK触发器的功能.
图8 电路是在图7 电路基础上,提出的具有异步置数功能的双边沿触发器电路.
图8 电路中,当M=0 时,F0,F6处于非交换状态,F2,F3和F4的控制位等于C,且预置数A从g5输出,对后面电路功能没有影响. 因此在M=0 时,图8 电路与图7电路等效.

图7 功能可配置的可逆双边沿触发器

图8 具有异步置数功能的可逆双边沿触发器
当M=1 时,F0,F6处于交换状态,且无论C为何值,F2,F3和F4的控制位信号始终为逻辑“1”,同时,F4和FG4构成的Latch 处于接受数据状态,接受的数据就是预置数A. 又因F2,F4和F6处于交换状态,预置数A可以直接输出到Q端,实现异步置数功能. 另外,当M=1 时,F5的控制位的值为“0”,F3和FG3构成的Latch 处于接受数据状态,接受的数据就是输出端Q的值,即为预置数A.
当M从1 变成0 时,无论时钟信号处于什么电平,处于锁存状态的Latch 寄存的数据一定是A,因此触发器的输出值保持预置数A不变,直到时钟触发边沿到来为止. 由此可得,在图8 电路中,不论C为何值,当M为高电平时可以实现异步置数,预置数为A.
6 可逆触发器功能仿真结果
为了验证提出的电路功能是否正确,本文用Ver⁃ilog HDL 语言对提出的可逆触发器电路进行了行为建模,并用Modelsim对电路逻辑功能进行了仿真.
图9 是图5 电路的仿真结果. 在0~t0时段,输入s=0,I1=I2,模拟可逆D 触发器功能,仿真结果显示输出Q符合D 触发器的逻辑功能.t0时刻以后,输入s=1,I1≠I2,模拟可逆JK 触发器功能,其中I1=J,I2=K,仿真结果显示电路输出Q符合JK 触发器的逻辑功能. 另外,从图9 可知,只有C从1 变成0 时,输出才发生相应变化,因此提出的触发器为下降沿触发.
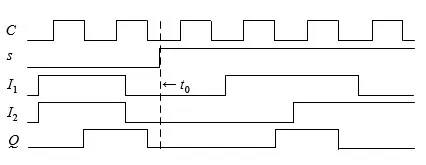
图9 可逆边沿触发器仿真结果
图10是图6电路的仿真结果,模拟JK触发器功能,输入s=1,I1=J,I2=K. 从仿真结果看,在M=1 时,虽然C和I2均发生了变化,但不影响预置数A的置入,使得输出Q=A=0保持不变;在M=0后,信号C下降沿到来之前,虽然I2发生了变化,但输出Q仍然保持不变,直到信号C下降沿到来后输出Q才随输入的变化而变化,输出Q符合边沿JK触发器行为,且具有异步置数功能.

图10 具有异步置数功能的可逆边沿JK触发器仿真结果
图11 是图7 电路的仿真结果. 输入s=0,I1=I2,模拟可逆双边沿D 触发器. 从仿真结果看,在C=1 或C=0 时,I1和I2的变化对输出Q没有影响. 输出Q的变化发生在信号C的上升沿和下降沿,且Q符合D 触发器行为.
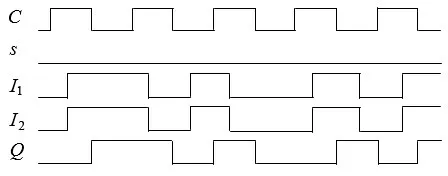
图11 可逆双边沿D触发器仿真结果
图12 是图8 电路的仿真结果,输入s=1,I1≠I2,模拟可逆双边沿JK 触发器. 从仿真结果看,在M=1 期间,虽然C,I1和I2发生了变化,但不影响实现预置数A的置入,且在M=1期间,预置数A的变化直接输出到Q端;在M=0 时,虽然I2发生了变化,但输出Q保持预置数值不变,直到时钟触发边沿到来后,输出Q才随输入的变化而变化,输出Q符合异步置数双边沿JK 触发器行为.

图12 具有异步置数功能的可逆双边沿JK触发器仿真结果
在可逆逻辑电路设计中,QC 常作为一个衡量可逆逻辑网络的构造成本指标. 可逆电路QC值等于构成该电路各个可逆逻辑门的QC值之和. 本文提出的电路仅使用Feynman 门和Fredkin 门,它们的QC 值分别是1 和5. 以本文图5 的单边沿触发器为例,该电路由3 个Fredkin 门和3 个Feynman 门构成,因此,图5 电路QC 值为3×5+3×1=18. 同理,图7电路的QC 值为24. 在表2中给出了其他文献提出的可逆D,T 和JK 边沿触发器的QC值. 其中T和JK边沿触发器是利用文献[14]提出的设计方法和使用的可逆门设计的,其对应的QC 值标有“*”号. 另外,由于已有文献中的可逆触发器均没有异步置数功能,因此,表2 中触发器电路均不含异步置数功能.

表2 与其他文献可逆触发器的QC值比较
从表2 可知,相比D 和T 触发器,本文设计的QC 值更大. 但实现JK 触发器时,本文电路的QC 值略小. 如以平均QC 值来衡量,本文提出的触发器与单一功能触发器相比,QC 值略增加2~3;但在逻辑功能上,本文提出的触发器要远比单一功能触发器丰富.
7 结语
本文主要开展了下面3 方面的工作:(1)在分析D,T和JK触发器次态方程基础上,将上述3种触发器的次态方程用一个新次态方程来描述,并通过适当配置新的次态方程中变量的取值,使新次态方程转化为D,T和JK触发器的次态方程;(2)利用提出的新的触发器次态方程,结合可逆Latch 提出功能可配置的可逆电平触发器,并在可逆电平触发基础上提出了功能可配置的边沿触发器和双边沿触发器;(3)提出了具有异步置数功能的可逆触发器电路,方便可逆时序电路设计中的电路初始化.
提出的各种可逆触发器电路用Verilog HDL 进行的行为级建模并仿真验证了提出的电路的逻辑功能可以配置且功能正确. 此外,相比于现有单一功能的可逆触发器,文本提出的触发器在增加有限QC 基础上,用一种电路结构实现了D,T 和JK 可逆触发器功能,电路功能得到显著扩展.
