抽水蓄能电站水力瞬变的有限体积法建模模拟
2022-07-02吴金远卢坤铭
周 领,吴金远,王 丰,刘 静,卢坤铭
(1.河海大学 水利水电学院,南京 210098;2.扬州大学 水利科学与工程学院,江苏 扬州 225009;3.中国三峡建工(集团)有限公司,成都 610041)
抽水蓄能电站作为现代电力中不可或缺的能源调节结构[1-2],有着调峰填谷、黑启动等功能[3]。然而,为了满足电力系统的动态服务要求,抽水蓄能电站有着一机多用、工况转换迅速、启停频繁等特点[4],常会导致整个机组产生较大的水力振动、共振等异常运行问题。因此,准确模拟各种水力瞬变对保证抽水蓄能电站安全稳定运行和精准控制极为重要。
目前,常采用特征线法(Method of characteristics,MOC)进行抽水蓄能电站水力瞬变的模拟计算。但是,抽水蓄能电站过流系统会涉及较多的短管、岔管、支管等情况,在特征线法求解中一般采取以下两种方法解决,一是插值计算,但会导致计算效率与精度的降低;二是调整波速或者网格长度,或者直接忽略短管,简化管网模型,相比于前者计算效率有所升高,但是会引入新的计算误差。
近年来,有限体积法(Finite volume method,FVM)逐渐被运用于有压管道水力瞬变计算。在保证系统质量与能量守恒前提下,FVM可以有效地处理非连续问题,避免虚假数值振荡。Guinot[5]最早将有限体积法运用于水锤问题,得到了和特征线法相类似的格式。随后,Zhao等[6]基于Godunov格式与Riemann求解器,得到了一阶和二阶的水锤求解格式。郑劼恒等[7]在顺序输送管道的水力瞬变中,采用有限体积法的Godunov格式,并通过Riemann求解器以及MUSCL方法对通量进行计算,从而有效避免了特征线法求解中的虚假振荡。Zhou等[8]将控制体等分,假定仅在控制体中心出现空穴,从而实现了Godunov格式对水柱分离-弥合水力现象的模拟。赵越等[9]研究了Godunov格式下库朗数、对流项等参数的敏感性。
为解决MOC在处理抽蓄管网系统工序复杂、精度较低的问题,本文采用二阶Godunov格式的FVM,并将虚拟边界与机组控制方程相结合,实现了对某抽水蓄能电站的水力瞬变模拟,并将结果与MOC计算值、实验值进行对比研究。
1 数学模型及其求解
1.1 水锤控制方程
对于管道内的非定常流,其连续方程和动量方程可写成如下的微分方程形式[10]:
(1)
(2)
式(1)~(2)可改写成矩阵形式:

(3)

式中:H为测压管水头,m;V为流速,m/s;g为重力加速度,m/s2;a为波速,m/s;D为管道直径,m;f为管道恒定摩阻系数;S0为管道坡度;x为沿管轴线距离,m;t为时间,s。
若采用Riemann求解格式进行求解,且不考虑对流项,则可将式(3)改为经典水锤方程:
(4)

有限体积法是将计算区域离散为多个单元体,并对各单元体单独积分求解,如图1所示。

图1 计算区域网格Fig.1 Grid of computational region
鉴于控制变量U在各时间和空间内均为连续分布,且在各控制体内分布平均,由此可得到相应的积分公式:
(5)
式中:i为第i个控制体;Fi+1/2为控制体右边界处的通量;Fi-1/2为控制体左边界处的通量;Δt为时间步长,s;Δx为空间步长,m;上标n表示t时刻;上标n+1表示t+Δt时刻。
1.2 水泵水轮机控制方程
1.2.1 全特性曲线
水泵水轮机的全特性曲线用以求解水泵水轮机在各瞬变时刻下各项特征参数的值。由于全特性曲线在各象限内均存在着开度线交叉、聚集、多值性等特点,因此在具体计算时需要对全特性曲线进行曲线转换。Suter变换[11]是在水泵水轮机中最常用的变换方式,其具体形式如下:
(6)
(7)
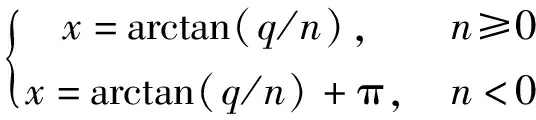
(8)
式中:WH、WM分别为水头特性函数和力矩特性函数,x为相对流量角,y为相对导叶开度,q=Q11/Q11r为相对单位流量,n=N11/N11r为相对单位转速,h=H/Hr为相对水头,m=M11/M11r为相对单位力矩,下标11表示单位值,下标r表示额定值。
但是常规的Suter变换无法表示0开度线下转速、流量、力矩间的关系,且常规的Suter变换后的曲线在小开度情况下曲线远稀疏于大开度情况下,导致计算结果在小开度情况下不够精确[12],而抽水蓄能电站在小开度情况下极易产生不稳定的情况。介于上述原因,本文采用改进的Suter变换[13],不仅可以表示0开度线下各参数的关系,对于小开度下曲线的疏密问题也有所改善,具体形式如下:
(9)
(10)
(11)
式中c为常数,一般取1.0~1.5,在本文计算中,c取1.2。其余各参数含义同式(6)~(8)。
1.2.2 机组边界条件
1)转速平衡方程。在机组全甩荷工况下,转速平衡方程如下[13-14]:
(12)
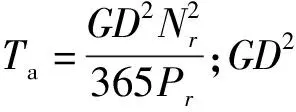
2)水头平衡方程。设蜗壳前和尾水管后压力钢管分别为节点1和2,对这两个节点分别用特征线方程,并带入水轮机水头计算方程,则可得到水头平衡方程[13-14]:
h=[Cp1-Cm2-(Bp1+Bm2)Qrq+C2|q|q]/Hr
(13)

联立式(9)、(10)、(12)和式(13),即可求出各瞬变时刻机组的水头、流量、转速、力矩等参数。
1.3 二阶Godunov求解格式
1.3.1 通量计算
由于各物理变量在各单位体内均是连续的,而在通量边界上是间断的,因此为求出Godunov格式下通量边界处的值,可采用Riemann问题的求解方式[15]:
(14)

由此,可求出各单元体在各边界处的通量值:
(15)
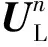
Step1数据重组。为避免重组数据时产生虚假振荡,分别引入MINMOD、MUSCL和SUPERBEE 3种斜率限制器函数,并在后文中分析比较其异同,则可得到:
(16)
(17)
式中,Δi由斜率限制器函数计算得到,对于MINMOD函数:
(18)
对于MUSCL函数:
(19)
对于SUPERBEE函数:
(20)
(21)
(22)
Step2推进时间计算。
(23)
(24)
Step3Riemann问题求解。
(25)
(26)
将求解出的式(25)、(26)带入式(15),则可求出各单元体边界处的通量。
1.3.2 时间积分
在得到二阶精度的通量计算值后要得到n时刻到n+1时刻的解,需要对式(5)进行积分求解,采用二阶显式Runge-Kutta,以得到二阶计算精度,计算过程如下:
(27)
(28)
(29)
若采用二阶求解格式的通量计算值,则式(27)~(29)所得到的格式在空间与时间上均为二阶精度。
1.3.3 虚拟边界
根据上述求解方式可知,在对任一单元体i进行二阶求解时,需要单元体i左右各两个单元体的物理变量值,因此对于边界处的单元体需要进行特定处理如图2所示。在本文中,采取在边界两边分别添加-1,0和N+1,N+2的虚拟单元的处理方法。

图2 计算区域与计算网格Fig.2 Computational region and grid
对于添加的虚拟单元满足以下条件:
U-1=U0=U1/2
(30)
UN+1=UN+2=UN+1/2
(31)
且各虚拟单元的物理变量分别满足边界处的Riemann不变量方程。
1)水库处。
对于上游水库,方程如下:
(32)
对于下游水库,方程如下:
(33)

2)机组处。
根据机组控制方程,只需求出蜗壳处与尾水管处的虚拟单元的物理变量值,便可求出机组在各瞬变时刻下的物理变量值。因此,结合Riemann不变量方程,可得:
(34)
(35)
(36)
(37)
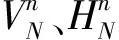
2 计算分析
2.1 简单管道系统算例
设置一上游为水库,下游为阀门的简单管道,管道长500 m,计算区域共10个,波速为1 000 m/s,上游水库为10 m,初始流速为0.1m/s,重力加速度为9.8 m/s2,总的计算时间取10 s,下游阀门设置为瞬时关闭,管道无模阻,则结果中的所有压力衰减均是由于数值耗散引起的。
分别用MOC和二阶Godunov格式的FVM对上述简单系统进行水锤求解,主要研究内容包括:1)比较分析MINMOD、MUSCL与SUPERBEE 3种斜率限制器函数对水锤计算的影响;2)研究库朗数Cr(1.0、0.5、0.2和0.1)对两种求解格式计算结果的影响;3)比较分析FVM与MOC水锤计算的精度和效率。
如图3(a)所示,当Cr=1.0时,MINMOD、MUSCL和SUPERBEE 3种斜率限制器函数计算完全相同;而如图3(b)所示,当Cr=0.5时,3种斜率限制器函数均会导致一定程度的数值耗散。然而,MUSCL与SUPERBEE会产生一定的虚假的数值振荡,而MINMOD计算更加稳定。因此,本文选择MINMOD斜率限制器。
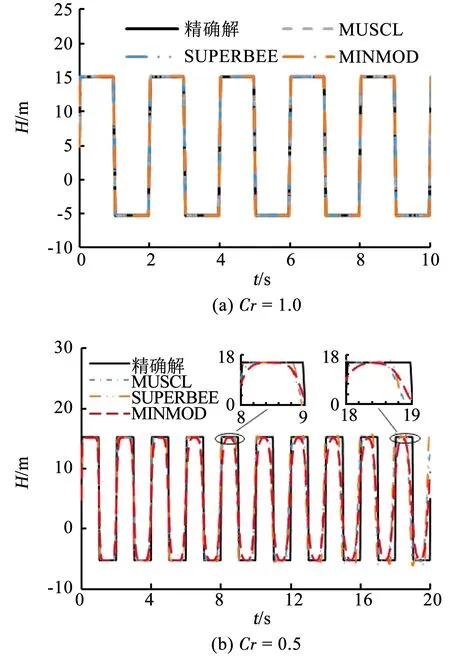
图3 不同斜率限制器在不同库朗数条件下的比对图Fig.3 Comparison of different slope limiters with different Courant numbers
如图4、5所示,当Cr=1.0时,两种方法计算结果与精确解完全相同,证明了二阶Godunov格式的FVM水锤计算的准确性。但是当Cr<1.0时,MOC和FVM均会出现不同程度的数值耗散,且Cr越小,耗散程度越严重。如图5所示,在相同库朗数条件下,二阶Godunov格式的FVM数值耗散远小于MOC。说明在Cr<1.0的条件下,二阶Godunov格式的FVM可以有效抑制数值耗散,计算更稳定,结果更精确。

图4 MOC计算结果Fig.4 MOC calculation results

图5 FVM计算结果Fig.5 FVM calculation results
如图6所示,当Cr=0.5时,网格数为512个的MOC格式与网格数为64个的FVM格式,计算精度基本一致。由表1可知,网格数为64个的FVM格式CPU计算时间为0.310 s,而网格数为512个的MOC格式CPU计算时间为1.080 s,约为FVM计算时间的3倍。说明在相同计算精度的情况下,FVM的计算效率要远远大于MOC。
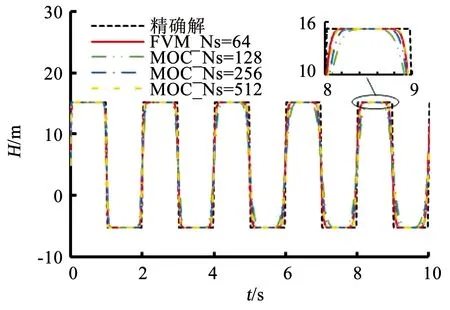
图6 FVM与不同网格数的MOC对比图Fig.6 Comparison of FVM and MOC with different grid numbers

表1 各模型计算时间Tab.1 Computational time of models s
2.2 某抽水蓄能电站水力瞬变计算分析
2.2.1 电站参数
电站设有两台150 MW的可逆式机组,上游引水系统采用“一管双机”、下游尾水系统采用“一管一机”的布置方式,布置如图7所示,相关设计参数见表2、3。

图7 某抽水蓄能电站布置图Fig.7 Layout of a pumped storage power station

表2 管道参数Tab.2 Parameters of water pipe system

表3 电站机组参数Tab.3 Unit parameters of power station
2.2.2 计算结果
在机组甩荷过程中,机组转速的波动是造成水轮机无法稳定运行最直接原因。因此将MOC和二阶Godunov格式的FVM计算出的转速与甩荷实验值进行对比。但是由于MOC在Cr<1.0时会产生较严重的数值衰减,因此需要对管道内波速进行调整,来满足Cr=1.0的条件。调整后的波速与管道分段数见表4。

表4 管道系统各部分管段波速及其分段数Tab.4 Section number and wave speeds of pipe system
本文选取了3组实验计算工况,已知3组实验工况的输入功率、初始流量与初始转速均为额定值,其他相关参数见表5。

表5 机组100%甩荷计算工况参数Tab.5 Calculation parameters of 100% load rejection
两种方法在整个计算时间段内计算的转速以及蜗壳处水头的变化情况见表6以及如图8~10所示。

表6 机组100%甩荷工况结果Tab.6 Calculation results of 100% load rejection (r·min-1)
由图8(a)、图9(a)、图10(a)所示,MOC与FVM在对该抽水蓄能电站模型进行甩荷计算时,计算结果与实验值基本吻合,表明二阶Godunov格式的FVM在处理较复杂管网模型时的适用性和准确性。由表6中数据与图8(a)、图9(a)、图10(a)所示,MOC与FVM计算的最大转速均略小于实验值,但FVM计算结果更加接近于实验值,这是因为MOC在计算过程中,需要对管道波速进行调整来满足库朗数条件,由此带来了一定的误差,且调整波速间接地增加了计算时间,导致其计算效率的降低。而FVM仅适当降低库朗数条件,无需进行波速调整,简化了计算过程,具有较高的计算效率与精度。

图8 甩荷实验1Fig.8 Load rejection experiment 1
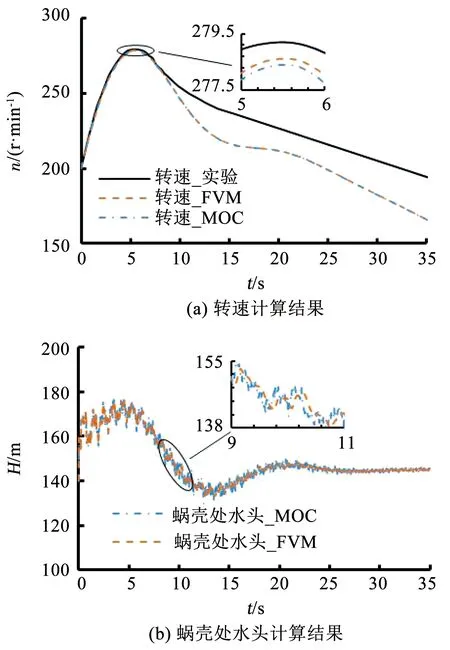
图9 甩荷实验2Fig.9 Load rejection experiment 2
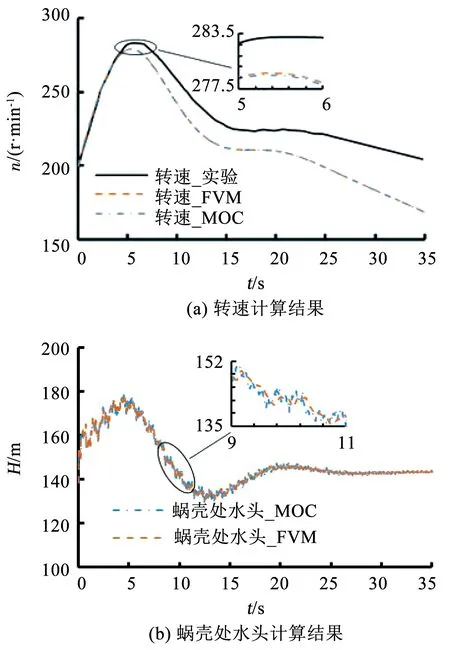
图10 甩荷实验3Fig.10 Load rejection experiment 3
由图8(b)、图9(b)、图10(b)所示,MOC与FVM地瞬变压力计算结果基本一致,但是很明显两者在转速变化较快时,均会产生一定的数值波动,但FVM计算结果相对更稳定。
本文进行该抽水蓄能电站模拟时进行了一定的简化处理,如忽略了平水建筑物的影响,从而导致机组转速达到最大值后的计算结果与实测数据存在一定的差异。不过,这对于本文结论的影响不大。
3 结 论
1)本文所建的二阶Godunov格式的FVM可准确、高效地实现对某抽水蓄能电站的水力瞬变计算模拟,且比MOC计算结果更接近实测值。
2)在二阶Godunov格式中,MINMOD、MUSCL与SUPERBEE 3种不同斜率限制器在Cr=1.0时均能得到精确的水锤结果;但在Cr<1.0时,3种斜率限制器函数均会导致一定的数值耗散,但MUSCL与SUPERBEE会产生虚假的数值振荡,而MINMOD计算更加稳定。
3)在Cr=1.0时,二阶Godunov格式的FVM和MOC两者计算结果一致。但是在Cr<1.0时,两种方法均会出现一定程度的数值耗散,但二阶Godunov的FVM可以有效地抑制数值耗散,计算更加稳定。
4)为了得到相同精度的计算结果,MOC需要更加密集的网格数,计算耗时长,而二阶Godunov格式的FVM在只需较稀疏的网格即可实现同样的计算精度,计算效率更加高效。
5)在处理抽水蓄能电站的水力瞬变问题时,MOC为了满足库朗数条件,需要进行波速调整,或者直接忽略短管,因而产生了计算误差;二阶Godunov的FVM仅适当降低库朗数条件,无需进行波速调整,简化了计算过程,具有较高的计算效率和精度。
