形貌对羰基铁/Fe-Si-Cr复合材料吸波性能的影响

金 丹，杜雨果，杨晓龙

(西安建筑科技大学 材料科学与工程学院，西安 710055)

近年来，随着电子科学的发展，电磁功能材料在电子科学、信息技术及自动化领域得到了广泛应用。电磁功能材料为人类活动带来巨大便利的同时，所产生的电磁辐射也造成了严重的电磁污染。电磁污染不仅会污染环境，影响电子设备的正常运行，同时会严重损害人类的身体健康，尤其是未来的智能时代，电磁抑制和衰减将成为治理电磁污染的关键问题。因此，抑制衰减电磁辐射是目前的研究热点。吸波材料能将电磁波能量转化为热能，是一种有效衰减电磁辐射的材料[1-5]。目前的吸波材料以涂覆型材料研究最广，它是以高分子溶液、乳液或液态高聚物为基体，把吸波剂分散加入后，制备而成的一种功能复合材料。其中吸波剂是决定吸波材料性能的关键因素，一般是粉末或纤维状，粉末又包括球状、片状、针状以及不规则形状。

CIP(Carbonyl iron powder)是一种铁磁性吸波材料，其以饱和磁化强度高、居里温度高和自然共振频率高的特点在微波吸收领域获得了广泛应用。但其损耗机制单一，介电常数在1～18 GHz频段内缺乏良好的频散特性，基本保持常数，与磁导率的频散特性无法匹配，故而难以满足宽频带吸收的要求[6]，并且CIP的抗氧化性、耐酸碱腐蚀性较差。Fe-Si系合金微粉具有较高的电阻率，较低的磁晶各向异性常数，并且在GHz频率下具有较高的微波磁导率，因此被广泛应用于电磁吸波剂[7]。Fe-Si-Cr做为Fe-Si系合金的典型代表，具有高的饱和磁化强度、高的居里温度以及高的自然共振频率。此外，由于Cr元素的引入，在一定程度上提高了合金的抗氧化性[8-10]。Kim等[11]对Fe-Si-Cr进行球磨，研究了其在S、L波段的吸波性能，在厚度为0.7，1.0，1.3，1.6 mm时的最大反射损耗分别为-5.6，-6.5，-8.5，-8.7 dB。洪起虎等[12]对Fe-Si-Cr进行球磨后使用硅烷偶联剂KH560对其表面改性。实验结果表明，改性处理前，Fe-Si-Cr在3.5 GHz处最大反射损耗为-12.0 dB；改性处理后，在4.0 GHz处的最大反射损耗为-14.0 dB；在表面改性处理后，材料具有了更好的抗高温氧化性能。可以看出，单一吸波剂的吸波性能并不理想。

通常，材料的电磁参数会受到粒子形状的影响。高频下，磁性吸波材料的磁性能主要受制于自然共振。对于球形粒子，由于本征各向异性很小，它的磁导率和共振频率都在Snoek的极限范围内，即随着自然共振频率的升高，初始磁导率会降低。将球形颗粒片状化，引入形状各向异性，使其自然共振频率提高到千兆赫兹以上，从而突破Snoek极限，获得更高的复磁导率实部和虚部[13-14]。然而，片状材料虽然提高了材料的磁导率，但同时也会造成较大的复介电常数，导致阻抗匹配特性恶化，阻碍吸波性能的提高[15]。因此，单一形貌的吸波材料，对于同时满足介电常数和磁导率相匹配，是较难实现的。值得注意的是，不同微观形貌的吸波剂具有不同的微波吸收性能，微观形貌对电磁吸收性能影响巨大。卢明明等[16]研究了不同形貌羰基铁的复合对材料电磁特性及吸波性能的影响。研究结果表明，球形羰基铁的加入，可以有效降低片状羰基铁的介电常数，优化复合材料的阻抗匹配。不同形貌羰基铁的复合材料，可以调控吸收峰在相应频率内的定向移动，增强材料的吸波强度并拓宽有效吸收带宽。当片状羰基铁和球状羰基铁质量比为1∶2时，复合材料在3.08 GHz处的反射损耗峰值为-20.2 dB，有效吸收带宽为2.43 GHz。

为解决羰基铁损耗机制单一，耐腐蚀性差的问题，将其与软磁合金Fe-Si-Cr进行复合。同时解决单一材料电磁参数不匹配，导致吸波性能差的问题。本文对球状Fe-Si-Cr进行扁平化处理，将不同形貌的 CIP和Fe-Si-Cr进行机械混合得到复合材料，讨论了不同形貌CIP和Fe-Si-Cr复合后对材料电磁参数的影响。通过控制质量比来实现电磁参数的优化，从而尽可能满足阻抗匹配，提升材料的电磁吸收性能。最后设计了双层吸波材料，旨在通过合理选择匹配层与吸收层、改变双层厚度来得到性能更加优异的吸波材料。

1 实 验

实验原料为球状CIP、片状CIP和球状Fe-Si-Cr。为了获得片状Fe-Si-Cr粉末，在行星球磨机上以330 r/min的转速对球状Fe-Si-Cr粉体进行机械球磨，球磨时间分别为40、50、60 h。以钢球为研磨介质，钢球直径为5 mm。粉末与球的质量比为1∶4。为了得到不同质量比的复合材料，将不同形貌的CIP和Fe-Si-Cr按照表1的质量比加入到无水乙醇中，机械搅拌使其混合均匀，磁选分离，60 ℃干燥12 h，得到复合材料。在制备待测样品时，选择石蜡作为黏合剂，其与吸波剂的质量比为3∶7。用扫描电镜(SEM，Quanta200)对其形貌进行了表征。用X射线衍射仪(XRD，D/MAX2200)对原料的相结构进行了表征。用微波矢量网络分析仪(Ceyear3762B-S)测量了材料在1～18 GHz的复介电常数和复磁导率。

表1 CIP与Fe-Si-Cr复合材料的比例Tab.1 Proportion of CIP and Fe-Si-Cr composites

2 结果与分析

2.1 XRD分析

图1为CIP和Fe-Si-Cr在10°～90°范围内的X射线衍射图谱。片状CIP和球形CIP的衍射峰位置基本相同。2θ=44.67°，65.03°，82.34°处对应α-Fe(JCPDS No.87-0721)(110)，(200)，(211)晶面所产生的衍射，未观察到其他杂质峰。在一些报道中可以看到，Fe-Si-Cr在2θ为25°～30°处会出现DO3超晶格相，但是在Fe-Si-Cr的XRD图谱中未观察到明显的特征峰[9,17-18]。因此，实验中使用的吸波剂均为单相CIP和Fe-Si-Cr。

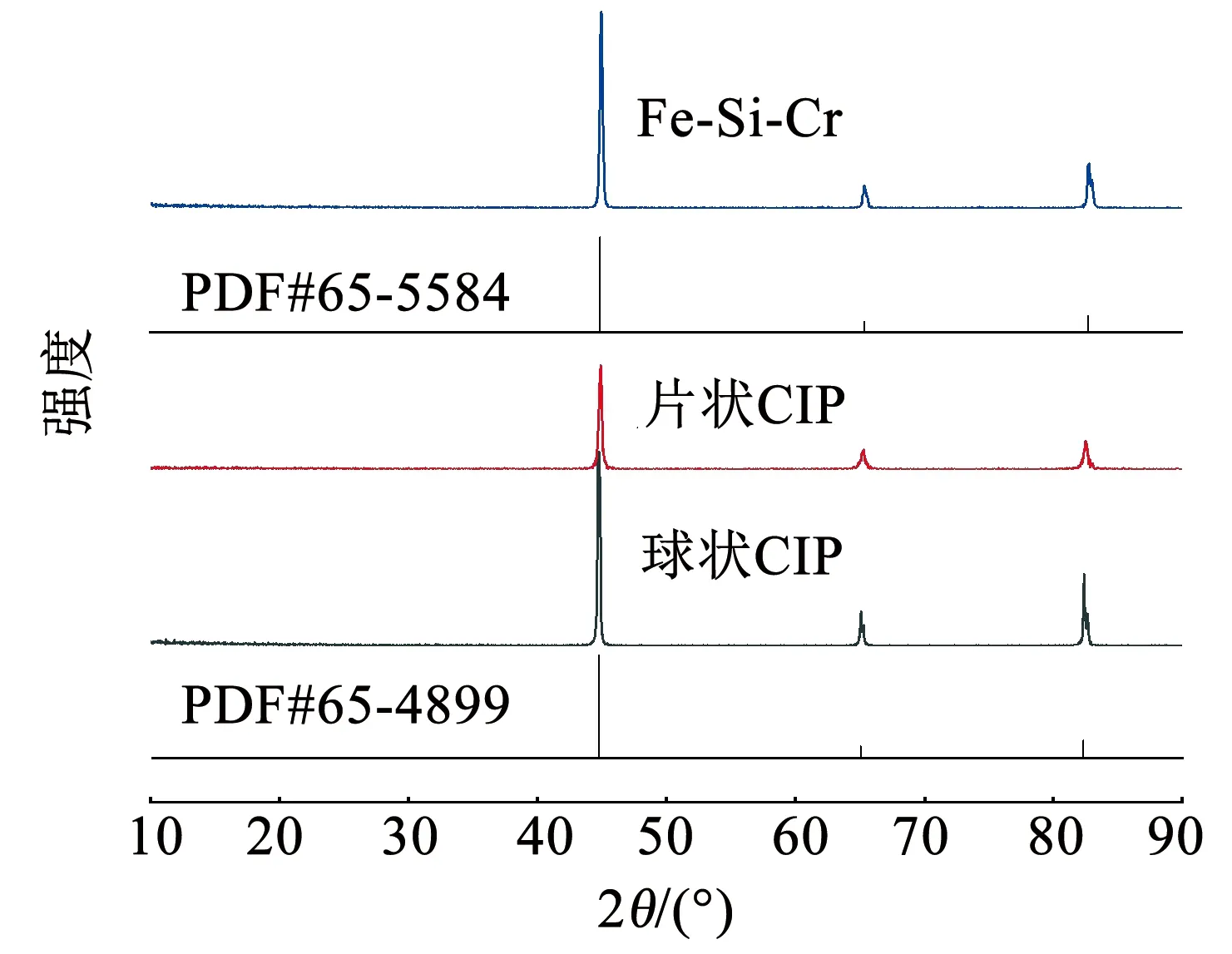
图1 CIP和Fe-Si-Cr的XRD图谱Fig.1 XRD patterns of CIP and Fe-Si-Cr

2.2 SEM分析

图2为不同形貌CIP和Fe-Si-Cr的SEM图。从图2(a)中可以看出球形CIP的形貌为规整的球状，平均粒径为3 μm。片状CIP形貌如图2(b)所示，表面光滑。球状Fe-Si-Cr磁粉具有良好的球形

结构，如图2(c)所示，球磨40 h后(如图2(d)所示)，出现大量片状结构，但仍可见少量球形颗粒。当球磨时间达到50 h时(如图2(e)所示)，形貌变化不明显。当球磨时间达到60 h时(如图2(f)所示)，球状颗粒基本消失，片状颗粒的长径比增大。因此，本实验选择了球磨60 h的片状Fe-Si-Cr合金。扁平化处理可获得大长径比的片状Fe-Si-Cr，在GHz范围内可以抑制涡流损耗，改善复磁导率[19]。

图2 不同形貌CIP和Fe-Si-Cr的SEM图Fig.2 SEM images of Fe-Si-Cr and CIP with different morphologies

2.3 单层CIP/Fe-Si-Cr复合材料吸波性能分析

对于吸波材料而言，复介电常数(εr=ε′-jε″)、复磁导率(μr=μ′-jμ″)和电磁阻抗匹配决定着电磁吸收性能[20]。介电常数的实部(ε′)和磁导率的实部(μ′)分别为电磁储能的能力，介电常数的虚部(ε″)和磁导率的虚部(μ″)分别为极化谐振引起的电磁损耗的能力[21]。

图3(a)、(b)分别为球状CIP、片状CIP、球状Fe-Si-Cr和片状Fe-Si-Cr的介电常数实部ε′和介电常数虚部ε″。相比于球状CIP，片状CIP的ε′和ε″明显增大，这与相关报道完全吻合。Fe-Si-Cr在经扁平化处理后，ε′增大，而ε″变化不明显。大长径比可以提高材料的导电性。根据自由电子理论，电导率与介电常数成正比，高导电性将导致高介电常数[22-23]。4个样品(A、B、C、D)的μ′和μ″值如图3(c)、(d)所示，样品的复磁导率实部(μ′)随频率的增大而减小。对于样品D，μ″在4.4 GHz处可以观察到一个共振峰，这是由畴壁共振引起的[24]。由图3(d)可知，样品B和D的μ″大于样品A和C

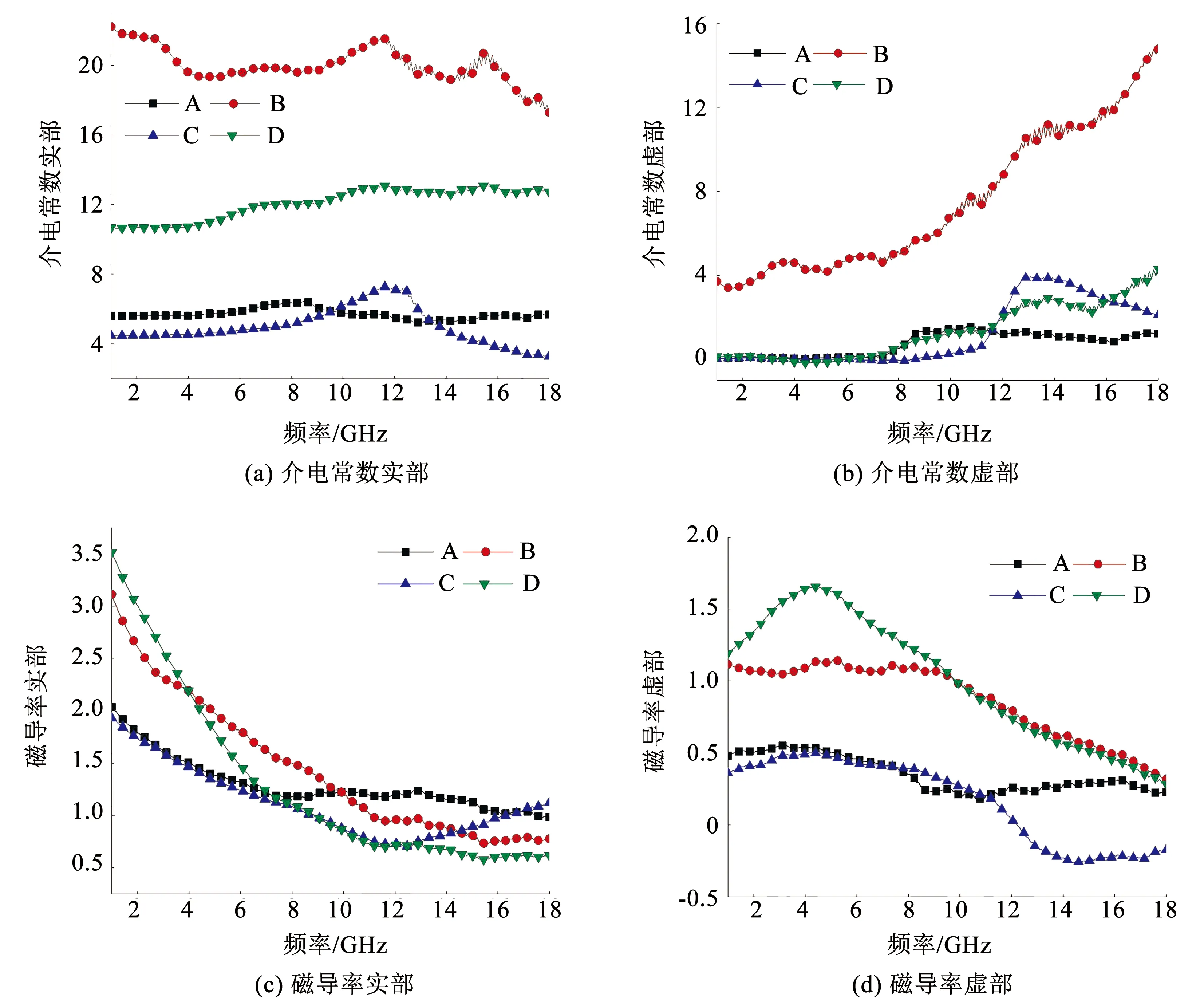
图3 不同形貌CIP和Fe-Si-Cr单一材料的电磁参数Fig.3 Electromagnetic parameters of Fe-Si-Cr and CIP single materials with different morphologies

的μ″。这意味着增加材料的长径比可以增强电磁波的损耗能力。样品C的μ″值在12.2 GHz后出现负值。Veselago[25]在1968年提出，负折射率材料(左手材料)具有“左手特性”，其介电常数和磁导率实部都为负值。然而样品C只有μ″为负值，因此这种现象不是材料的左手特性。μ″在高频处出现负值，第1个可能性是与测试系统有关的法布里-珀罗谐振，第2个可能性是电能-磁能转换效应[26-27]，在时变电磁场中，根据能量守恒定律，磁场能量的增加应由电场能量的降低引起。此外，Deng等[28]发现多壁碳纳米管/石蜡复合材料具有负μ″值的现象，本文认为这是由于磁能从复合材料中辐射出来导致的。从图3(a)、(c)中可以看出，在12 GHz后，样品C的ε′值下降，μ′值增大，这意味着电场能量的降低，磁场能量的增大，同时μ″出现负值。μ″为负值，表示复合材料被电磁波照射后，磁场能量没有降低，而是增加[26]。

图4为复合材料的复介电常数和复磁导率。由图4(a)、(b)可以看出，复介电常数的实部(ε′)随频率的增加略有减小，样品H、I、J的ε′最大，其次是样品E、F、G，最后是样品K、L、M。可以看出扁平化处理可以改善ε′。然而，复介电常数(ε″)的虚部在13～18 GHz范围内波动，这是由于不同尺寸和形状的颗粒具有大量的介电弛豫过程和不同的弛豫时间所致[29]。因此，在图4(b)中可以观察到多个共振峰。样品H、I、J的介电常数虚部随着频率的增大呈增大趋势。这是由于复合材料中存在定向极化及空间电荷极化。定向极化主要受材料中束缚电荷的影响。此时定向极化、介电弛豫和共振突出，使得介电常数虚部呈增加趋势。所有样品的复磁导率实部(μ′)均随频率的增加而减小。样品K、L、M的磁导率虚部(μ″)在1～18 GHz范围内最小，样品H、I、J在1～18 GHz范围内最大。这是由于片状粒子的各向异性，使得片状粒子具有比球状粒子更高的磁导率。所有样品的磁导率随着频率的增大呈减小趋势。这是由于频率越高，涡流损耗越大，产生的反向磁场也越大，使得高频磁导率降低[30]。样品在低频处可以观察到磁导率虚部出现一个共振峰，这归因于材料的自然共振。

图4 不同质量分数CIP/Fe-Si-Cr复合材料的电磁参数Fig.4 Electromagnetic parameters of CIP/Fe-Si-Cr composites with different mass fractions

根据德拜理论，ε′与ε″的关系可表示为

(1)

式中εS、ε∞分别为静态介电常数和无限频率下的介电常数[31]。从图5(a)～图5(e)中可以看出，3种样品都存在Cole-Cole半圆，说明复合材料中存在弛豫极化过程。对比样品F、I、L的横、纵坐标，样品I的值最大，L的值最小。可以说明，长径比增大后，材料的比表面积增大，材料的空间电荷极化和界面极化加强。

理论上，磁损耗主要来自畴壁共振、磁滞损耗、自然共振和涡流损耗。磁滞损耗的主要原因是磁化矢量的响应滞后于外场的响应。在微波场存在的情况下，由于微波场较弱，磁滞效应可以忽略[32]。畴壁共振损耗主要发生在MHz范围，而不是GHz范围。因此，可以排除畴壁共振对微波磁导率的贡献。涡流损耗与样品的厚度和电导率有关，可用下式表示[33]:

μ″(μ′)-2f-1=(2/3)πμ0d2σ

(2)

式中：σ为电导率，μ0为真空磁导率。从图5(f)中得出，样品E的涡流损耗最大，样品H、I、J次之。将不同形貌的CIP和Fe-Si-Cr复合后，通过调整质量比，可以改变复合材料的涡流损耗。同时根据式(2)可知，如果材料中的磁损耗仅来自涡流损耗，则方程左侧的值应为不随频率变化的常数。由图5(f)可知，样品的涡流损耗值随频率的增加有明显的变化。由此可见，涡流损耗不是样品的主要损耗，样品的磁损耗主要来源于自然共振和交换共振。

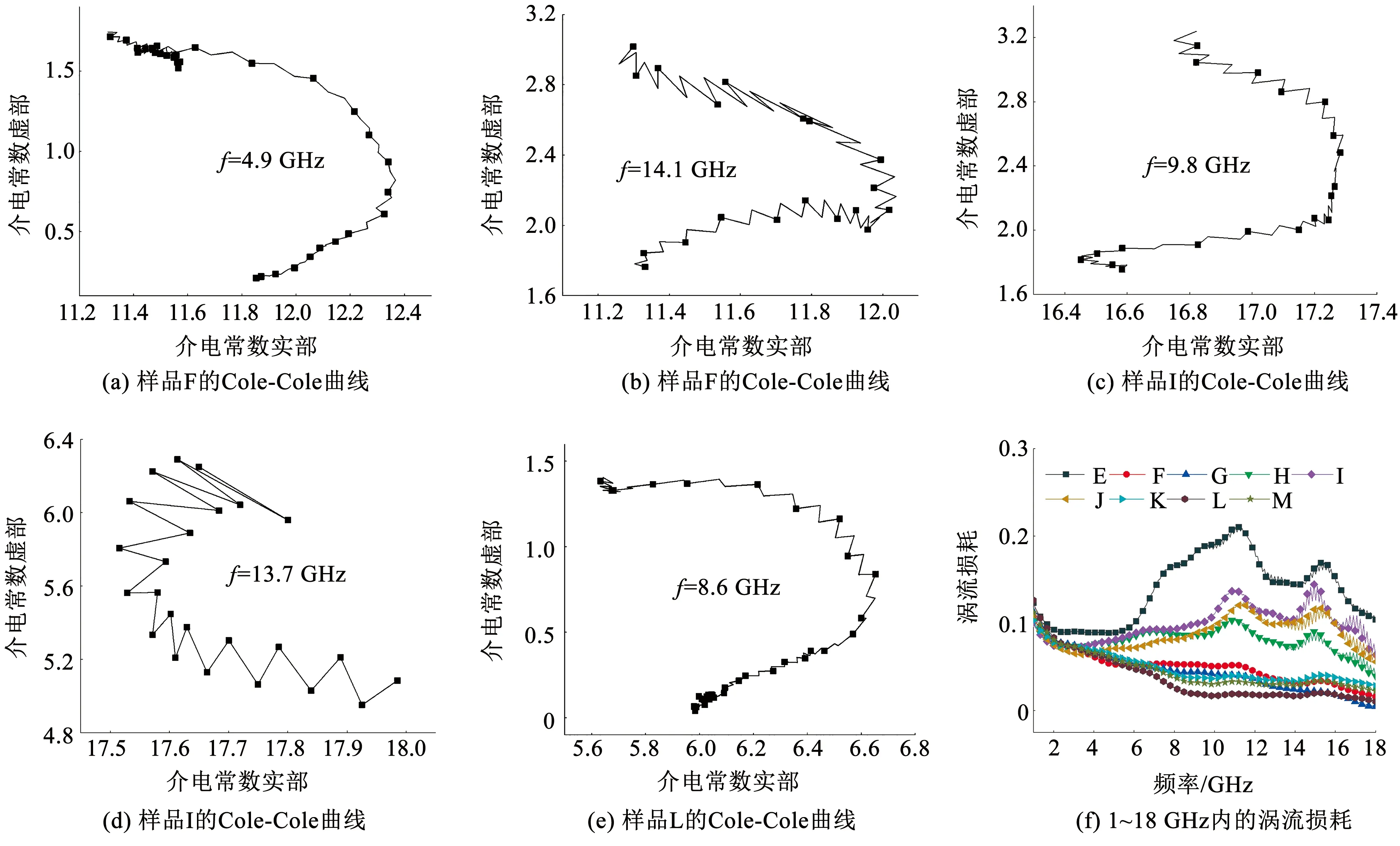
图5 不同样品的Cole-Cole曲线和不同复合材料的涡流损耗曲线Fig.5 Cole-Cole curves of different samples and eddy current loss of different composites

图6(a)是由单一原料制备的样品的反射损耗。片状样品的反射损耗峰值在低频区域，而球状样品的反射损耗峰值在高频区域。图6(b)是复合材料厚度为2.5 mm的反射损耗，将片状和球状的吸波剂复合后，反射损耗峰值位于球状/球状和片状/片状复合材料之间。因此，选择不同形貌的CIP和Fe-Si-Cr复合，通过改变复合材料配比及厚度，可以有效调整反射损耗峰值所对应的吸波频率。

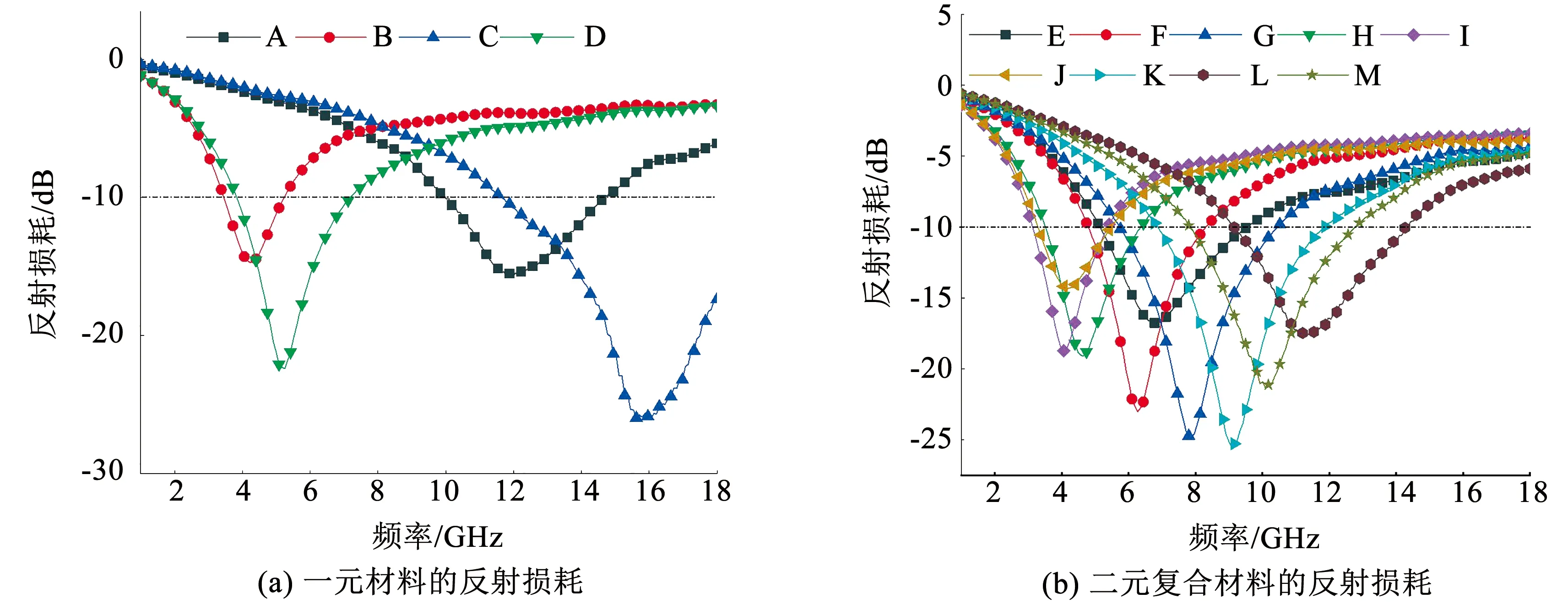
图6 所有样品(A～M)厚度为2.5 mm时的反射损耗Fig.6 Reflection loss of all samples (A-M) with thickness of 2.5 mm

图7展示了不同形貌CIP和Fe-Si-Cr质量比为1∶1时的反射损耗。

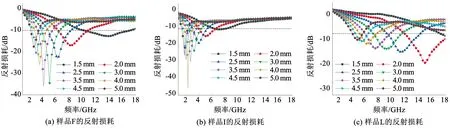
图7 样品F、I、L在不同厚度下的反射损耗Fig.7 Reflection loss of samples F, I, and L at different thickness

表2给出了具体的反射损耗峰值及有效吸收带宽。可以看出，样品F、I虽然具有较大的反射损耗，但其有效吸收带宽窄；样品L的反射损耗小，但是其有效吸收带宽大于6.29 GHz。

表2 复合材料的反射损耗峰值(RL)、峰值频率和有效吸收带宽Tab.2 Peak reflection loss, peak frequency, and effective absorption bandwidth of composites

与反射损耗有关的一个重要参数是阻抗匹配度，它反映的是吸波材料的特性阻抗与自由空间的特性阻抗的接近程度，两者无限接近时，阻抗匹配度|Δ|会无限趋近于0，从而实现零反射。如果复介电常数远大于复磁导率，则表面电阻较低，导致大多数入射电磁波不会被传输到吸收材料中，而是被表面反射。因此，阻抗匹配度是复介电常数和复磁导率的函数，在下面的方程中给出了这一关系[34-36]：

|Δ|=|sinh2(Kfd)-M|

(3)

式中K、M分别为通过复磁导率和复介电常数,用以下公式计算：

(4)

(5)

(6)

根据式(3)～式(6)，计算了样品F、I、L的阻抗匹配度，分别对应图8中的图8(a)～图8(c)。

从图8(b)中可以看出，样品I在低频大厚度和高频小厚度处，阻抗匹配度小于0.202，说明此时材料具有较好的匹配特性，有利于吸收衰减电磁波，这与图7(b)的反射损耗曲线相一致。将图8(c)与图8(a)、(b)进行对比，阻抗匹配度的曲线向高频移动。这是由于，样品L为球状CIP与球状Fe-Si-Cr的复合材料。而各向同性材料在低频段具有良好的吸波性能，这与图7中的计算结果相一致。并且通过图8可以看出，在出现最大反射损耗的频率及厚度处，都具有较小的阻抗匹配度。

图8 样品F、I、L在1～18 GHz频率范围内的|Δ|值，吸收层厚度从0～5 mmFig.8 |Δ| value of samples F, I, and L in frequency range of 1-18 GHz, and thickness of absorption layer from 0 to 5 mm

为了解释吸波机理，给出了示意图，如图9所示。CIP和Fe-Si-Cr的三维空间，以及片状Fe-Si-Cr的大长径比，扩展了电磁波的传播路径，引起了电磁波的多次反射。输入的电磁波局限于材料内部，在复合材料内部衰减，导致电磁波以热能的形式耗散。同时，复合材料之间存在丰富的界面，会产生大量的界面电子极化，从而增加电磁波的损耗，对提高微波吸收起着关键作用。

图9 CIP/Fe-Si-Cr复合材料的微波吸收机理示意图Fig.9 Schematic illustration of possible microwave absorption mechanisms in CIP/Fe-Si-Cr composites

2.4 双层CIP/Fe-Si-Cr复合材料吸波性能分析

对于吸波材料的阻抗匹配，是由给定频率下的复介电常数和复磁导率以及吸波体的厚度共同决定；而阻抗匹配值又决定吸波材料的电磁吸收性能[37]。因此，如果可以实现设计双层吸波材料，通过选择合适材料作为匹配层和吸收层，将有效优化材料的阻抗匹配，提升电磁吸收性能。当电磁波垂直入射到双层吸收材料时，反射损耗可由以下公式计算[38-39]：

(7)

(8)

(9)

式中：ε1、μ1分别为第1层的相对复介电常数和相对复磁导率,ε2、μ2分别为第2层的相对复介电常数和相对复磁导率,Z1为第1层的和第2层的界面阻抗,Z2为自由空间和第2层的界面阻抗,t1、t2分别为第1层和第2层的厚度,f为频率,c为自由空间中的光速。

为了研究双层吸波材料的吸波性能，根据式(7)～式(9)，对不同厚度材料的反射损耗进行了计算。图10展示了不同单一材料作为第1层和第2层的反射损耗。

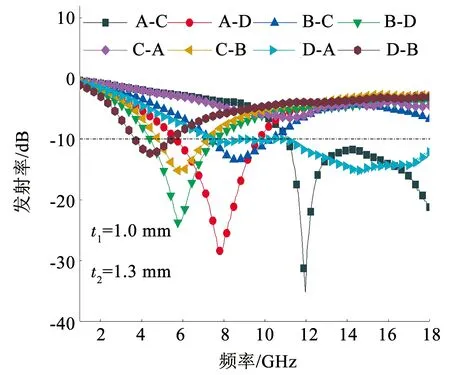
图10 不同单一材料作为第1层和第2层的反射损耗Fig.10 Reflection loss of different single materials as first and second layers

从图10中可以看出，在第1层厚度为1.0 mm，第2层厚度为1.3 mm的情况下，以球状CIP作为第1层的反射损耗要明显大于Fe-Si-Cr，A-C的反射损耗在11.97 GHz处达到了-35 dB，在14.43 GHz处出现了新的拐点，之后随着频率的增大，反射损耗又继续增大，有效吸收带宽>6.89 GHz。因此，在后续工作中，选择球状CIP作为第1层，复合材料作为第2层。

图11展示了第1层为球状CIP(样品A)，第2层为w(CIP)40%+w(Fe-Si-Cr) 60%复合材料的双层反射损耗。可以看出，A-E的反射损耗在13.41 GHz处出现反射损耗峰值，有效吸收宽度为6.50 GHz。同时可以看出，球状复合材料在高频下出现反射损耗峰值，而片状复合材料在低频出现反射损耗峰值，将不同形貌的材料复合之后，反射损耗峰值出现在两者之间，这与单层吸波材料具有相同的规律。在后续工作中，选择不同形貌复合的材料，通过改变双层厚度，来调节最大反射损耗的位置。

图11 第1层(A)和第2层(E,H,K)组成的双层吸波材料的反射损耗Fig.11 Reflection loss of double-layer absorbers consisting of the first layer (A) and the second layer (E, H, K)

图12(a)展示了总厚度为2.5 mm的双层吸波材料的反射损耗，其由不同厚度的样品A(第1层)和样品E(第2层)组成。当第1层厚度从0.5 mm增加到2.0 mm时，反射损耗峰值向高频移动。当第1层厚度为1.0 mm，第2层厚度为1.5 mm时，反射损耗峰值在8.82 GHz时为-31.42 dB，有效吸收带宽为4.50 GHz。这意味着，两层在这一匹配厚度下耦合。

因此，选择第1层(样品A)厚度为1.0 mm，改变第2层厚度，研究第2层厚度对电磁吸收性能的影响，反射损耗如图12(b)所示。可以看出，随着第2层厚度从1.0 mm增加到2.4 mm，反射损耗向低频移动。第2层厚度为1.6、2.0 mm时，分别在8.31、6.78 GHz处，反射损耗峰值为-44.2、-44.4 dB，有效吸收带宽分别为4.34、3.91 GHz。通过改变第2层厚度，可以增强材料的电磁吸收强度。

图12 不同双层吸波材料的反射损耗Fig.12 Reflection loss of different double-layer absorbers

3 结 论

1)采用机械球磨法对球状Fe-Si-Cr进行了扁平化处理。大长径比有利于材料的反射损耗向低频移动。吸波剂的形貌对材料的电磁吸收性能有很大影响。将不同形貌的CIP和Fe-Si-Cr按不同配比复合后，可以得到不同频率下性能优良的吸波体。

2)设计了不同匹配层，吸收层以及不同厚度下的双层吸波体。相较于单层吸波体，双层吸波体可以满足强吸收、宽频带和薄厚度的要求。样品A-C的反射损耗峰值在11.97 GHz处达到了-35 dB，有效吸收带宽>6.89 GHz。通过调整匹配层和吸收层的厚度，可以获得不同频率下吸波性能优良的吸波体，当第1层厚度为1.0 mm，第2层厚度为1.6 mm时，双层吸波材料的反射损耗峰值为-44.2 dB，有效吸收带宽为4.34 GHz。因此在实际应用中可以通过调整双层厚度来满足实际需求。