双向多尺度LSTM的短时温度预测

程鹏宇,赵 嘉*,韩龙哲,张翼英,武延年

(1.南昌工程学院信息工程学院,江西 南昌 330099;2.天津科技大学人工智能学院,天津 300457;3.深圳市国电科技通信有限公司,广东 深圳 518000)

0 引言

全球变暖引起气候变化,导致极端天气事件急剧增加[1].极端天气对人类生产和生存环境的影响逐渐增大,极端高温与低温带来的损失非常严重.极端高温可能会引发中暑、心脑血管疾病、系统呼吸疾病等病症[2].因此,深入研究温度变化规律,提高温度预测的准确度,具有重要的现实意义,有关温度预测的研究正受到人们的普遍关注[3].

传统的温度预测是通过建立大气模型模拟天气,搭建温度预测系统[4],建立的模型需要精确模拟真实的气象变化,但该方法实际操作比较复杂.目前,大多数研究方法是基于数学模型的温度预测,如支持向量回归[5]、随机森林[6]、概率图[7]等,但这类模型的预测精度不高.随着数据分析[8]、回归分析及深度学习[9-10]在众多领域中的发展,温度预测也有了新方法.为了提升模型的预测精度,学者们提出了基于神经网络的温度预测模型[11-13].

循环神经网络(recurrent neural network,RNN)[14]是以序列数据为输入,进行递归且按链式传递的递归神经网络.循环神经网络具有记忆性、参数共享的特点,在处理时序数据时具有一定的优势,但存在梯度消失、爆炸和长期依赖等问题.1997年S. Hochreiter等[15]提出长短期记忆网络(long short-term memory,LSTM).LSTM在RNN的隐藏状态中添加了门控单元,解决了长期依赖和梯度消失、爆炸问题.近年来,学者们开始关注循环神经网络如何提取序列数据的多尺度特征,如时钟神经网络(clockwork recurrent neural network,CW-RNN)[16]、分层多尺度循环神经网络(hierarchical multiscale recurrent nerual networks,HM-RNN)[17]、多尺度RNN(dilated recurrent neural networks,DiRNN)[18]、多尺度跳跃深度LSTM(multi-scale skip deep long short-term,MSD-LSTM)[19]等.DiRNN通过添加多个指数增长多尺度循环跳跃连接提取在数据中的多尺度特征;MSD-LSTM选择数据的年、月、日的周期数作为跳跃连接数,上述2种模型的预测精度都得到了明显提升.但这些模型依然存在如下缺陷:(i)只考虑数据的多尺度特征,忽视了数据的反向特征;(ii)月周期或按照指数增长的跳跃连接数,在循环神经网络隐含层中跳跃周期太长,存在较大的局限性,不适合对短期数据进行建模.

针对上述问题,本文提出了双向多尺度跳跃LSTM(bidirectional multi-scale skip long short-term memory,BMS-LSTM)短时温度预测模型.BMS-LSTM模型使用双向深层网络结构,以LSTM为核心,设置多个跳跃连接数提取多尺度时序特征和反向特征.区别于指数增长的跳跃连接数,该模型使用日周期对温度数据进行建模;使用双向网络结构,提取数据的反向特征.

1 双向LSTM

1.1 LSTM

RNN具有参数共享、记忆等特点,对序列数据建模具有巨大优势.RNN隐含层通过迭代处理信息,且在更新迭代时依赖前一隐含状态,保存了数据之间的信息.然而,在使用RNN对序列数据进行建模时,依然存在如下缺陷:(i)无法或者很难记忆长期依赖;(ii)在反向传播训练RNN时会发生梯度消失和爆炸.为了克服这些困难,S. Hochreiter等[15]提出的LSTM弥补了RNN的缺陷.LSTM与RNN区别在于细胞状态(见图1).LSTM设计了3个门结构来控制状态信息的流通和损失,包括遗忘门ft、输入门it及输出门ot.

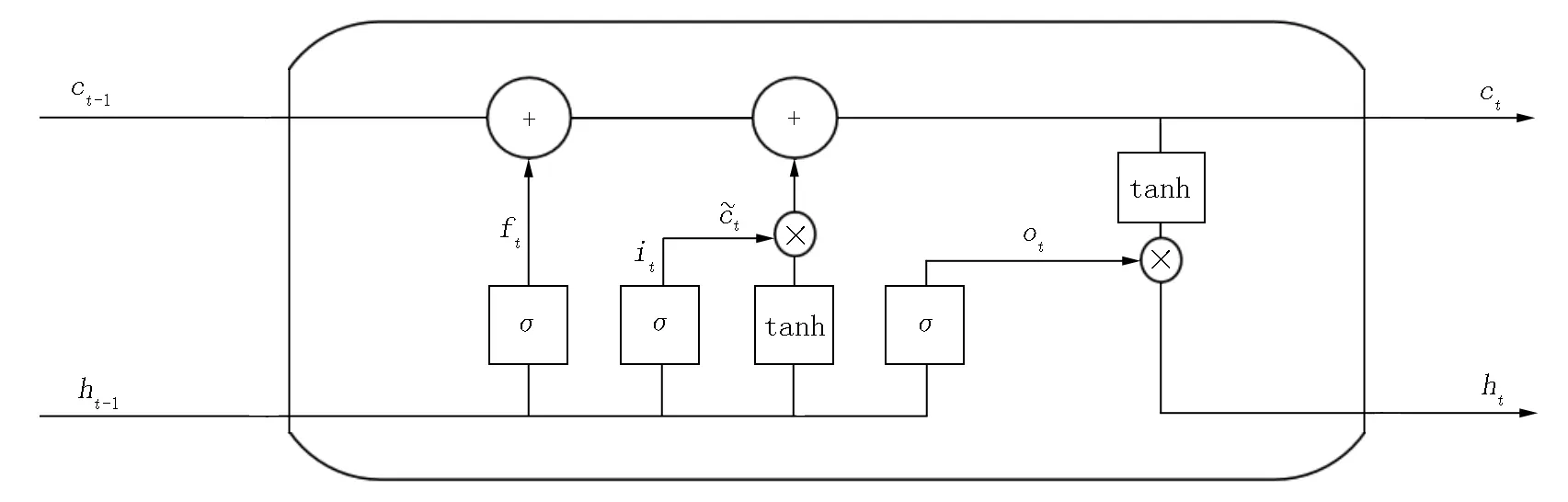
图1 LSTM细胞状态

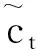
ft=σ(Wf[ht-1,xt]+bf),

it=σ(Wi[ht-1,xt]+bi),

ot=σ(Wo[ht-1,xt]+bo),ht=ottanh(ct),

其中σ为sigmoid()函数,[]为矩阵拼接,Wf、Wi、Wc、Wo分别为遗忘门、输入门和输出门的权重.bf、bi、bc、bo分别是各门的偏置值.sigmoid(x)函数将实数x映射到(0,1)区间,计算方法为

sigmoid(x)=1/(1+e-x).

tanh(x)为双曲正切函数,它将实数x映射到(-1,1)之间,计算方法为

tanh(x)=(ex-e-x)/(ex+e-x).

1.2 双向LSTM

RNN处理时序数据的顺序是由前往后单向进行的,即当前时刻的输出依赖之前时刻的状态.但某些数据当前时刻的输出不仅与之前的状态相关,而且和未来的状态也息息相关.对于此类数据,RNN无法提取其反向特征,这导致预测精度降低.为弥补此缺陷,M. Schuster等[20]提出了双向RNN,双向RNN的隐藏状态分为正序和逆序2种状态.正序状态是指当前状态依赖之前时刻的隐藏状态,逆序状态是指当前状态依赖后面时间步的隐藏状态.因此,双向RNN能提取数据的反向特征,从而提高了预测精确度.图2为按时间步展开的双向RNN结构图,各层中计算方法分别为

图2 双向RNN结构图

其中H()、G()表示激活函数,根据实际情况可任意选取.在本文中H()选用tanh()函数,G()选用sigmoid()函数.

A. Graves等[21]提出了双向LSTM(bidirectional long short-term memory neural network,BiLSTM)模型,并将其应用于语音信息建模.双向LSTM结合了双向RNN和LSTM的优势,在提取双向特征的同时,能有效解决长期依赖和梯度消失、爆炸问题,提升了模型的预测精度.双向LSTM凭借其优势,得到了广泛应用,如股票预测[22]、负荷预测[23]和温度预测[24]等.

2 BMS-LSTM短时温度预测模型

BMS-LSTM短时温度预测模型可同时提取在序列数据中的双向特征和多尺度特征.温度数据存在明显的周期特性,主要体现在年、月、日时间期限上的循环特性.本文实验使用720 h(30 d)的温度数据来预测未来24 h的温度,即模型输入的时间步长为720,当模型的输入只有30 d的数据时,无法体现年、月的循环特性,因此设计出的模型仅考虑提取日循环周期的多尺度特征.模型的第1层跳跃连接数设为1,即标准的BiLSTM;第2层的跳跃连接数设为24,即时间步更新状态依赖前24个时间步的隐藏状态;第3层跳跃连接数设置为48,这表示当前时间步更新依赖前48个时间步的隐藏状态;第4层跳跃连接数设置为72,这表示当前时间步更新依赖前72个时间步隐藏状态.把模型的4层跳跃连接数依次设为1、24、48、72,就可提取数据的多尺度特征.最后添加2个全连接层,拼接每层的输出作为全连接层的输入,实现多尺度特征融合.最后,全连接层的输出作为模型的预测值.

BMS-LSTM模型架构如图3所示,每层设置不同的跳跃连接数[19],使每个时间步的状态信息不是依赖前一时间步的隐含状态,而是依赖多个时间步之前的隐含状态.时间步之间的更新方法为

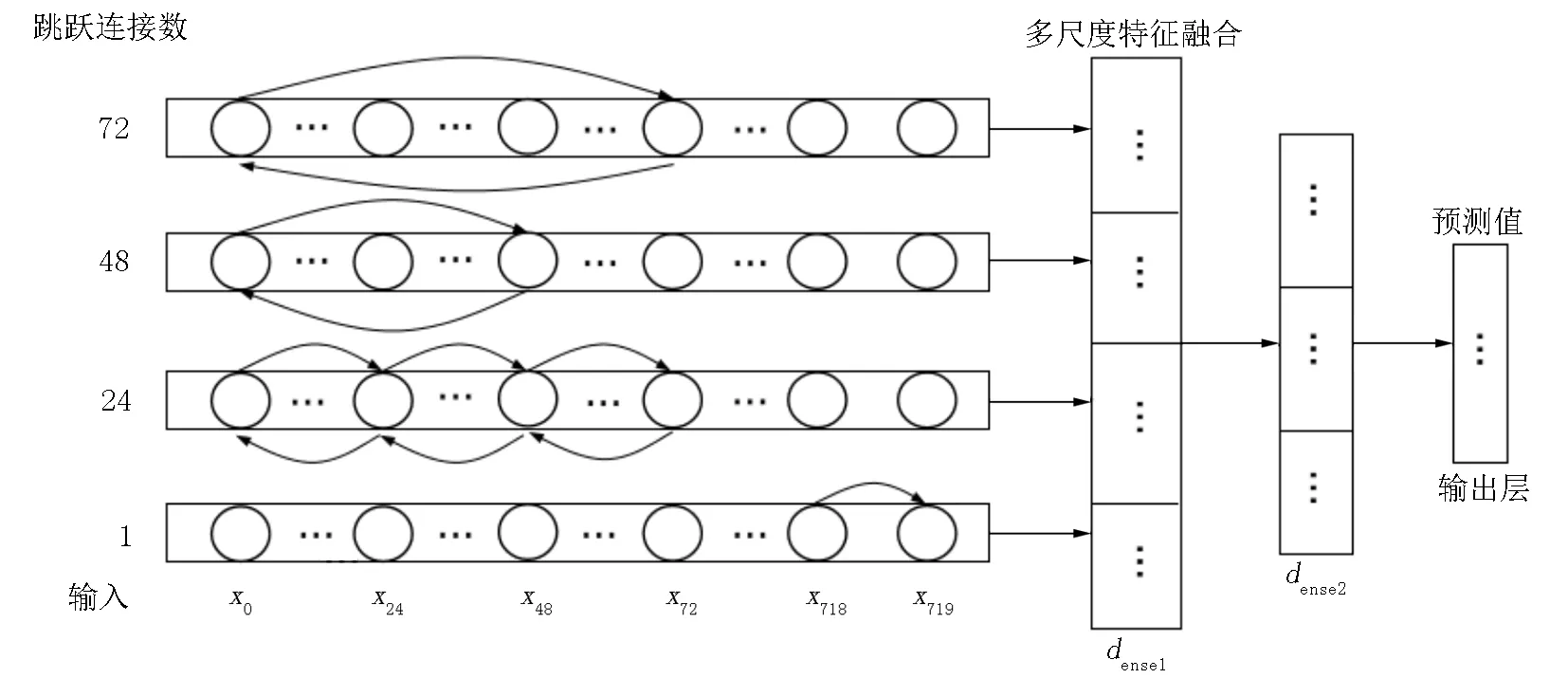
图3 BMS-LSTM模型

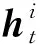
全连接层的传播的计算方法为

Y1=wd1H+b1,Yout=wd2Y1+b2,

其中wdi为第i层全连接层的权重,bi为第i层的偏置.H为第1层全连接层的输入,H的计算公式为

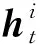
3 实验分析与比较

3.1 数据预处理

实验使用的数据来源于欧洲某城市2015年1月1日—2018年12月31日的天气数据,包括温度、风速、压强、湿度、风向等.将上述5个天气数据拼接为一个5维向量,通过融合其他天气数据,提高短时温度预测精度.

模型使用720个时间点的数据预测未来24 h的温度,样本数据维度为720×5.天气数据的数值差异较大,不利于模型的预测,因此实验前需要对数据进行归一化处理.将数据随机分为14组,前13组样本作为训练集,最后一组为测试集.每次实验均将数据重新随机分组,使每次实验的训练集与测试集都不相同.样本的原始数据为X=[x1,x2,x3,x4,x5]720,数据归一化处理的方法为

其中t∈[0,1,2,3,…,718,719],即对应的是网络层的时间步;i表示列数,即某一天气数据;min()、max()是最小值和最大值函数.

3.2 实验设置

本实验环境的主要参数:处理器是Intel(R) Core(TM) i7-9750H CPU@2.60GHz;显卡为NVIDIA GeForce RTX2060 8G;内存为16 GB;操作系统是Windows10家庭中文版;使用Tensorflow构建模型并进行训练与测试.

实验使用多层LSTM(MLSTM)模型、双向MLSTM[20]和多尺度跳跃深度LSTM[19](Multi-scale skip deep long short-term memory,MSD-LSTM)与BMS-LSTM模型进行对比.

MLSTM模型层数设为4,与MBiLSTM模型对比,检验双向深层网络结构相比于深层网络结构性能是否得到了提升.MBiLSTM模型层数设为4,检验BMS-LSTM模型是否有效提取数据的多尺度特征.MSD-LSTM和BMS-LSTM模型层数均设为4层,将它们进行对比,检验BMS-LSTM是否可以提取数据中反向特征.所有模型的神经单元个数均设为32,采用RMSprop算法对参数进行优化,学习率为0.002,损失函数为平均绝对误差函数.

MLSTM、MBiLSTM、MSD-LSTM和BMS-LSTM

模型在训练时采用mini-batch技术(batch_size为100),可加快模型的学习速度,同时有利于参数更加鲁棒性的收敛.除此之外,为了防止模型过拟合,所有模型都使用Dropout技术,Dropout率设为0.5.

3.3 实验结果及分析

本文进行了8次实验,采用平均绝对误差(mean absolute error,MAE)eM作为评判标准.eM计算方法为

(1)

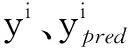
对比实验结果如表1所示,表1中的数据是利用式(1)计算的平均绝对误差,数值越小说明模型预测精度越高.从表1可以看出,由于BMS-LSTM采用双向深层网络结构,提取了数据的反向特征,设置多个跳跃连接数提取了多尺度特征,所以对比其他3种模型,BMS-LSTM均表现出较好的结果.BMS-LSTM模型实验的平均预测误差约为3.890,远小于MLSTM和MSD-LSTM模型的误差.虽然MBiLSTM模型的平均预测误差为4.980,与BMS-LSTM的误差仅差1.1左右,但由表1数据显示:MBiLSTM的预测精度忽高忽低,极不稳定.而BMS-LSTM模型8次实验预测精度较稳定,一直保持在3.890左右.综上所述,BMS-LSTM预测精度最高,预测效果最稳定.

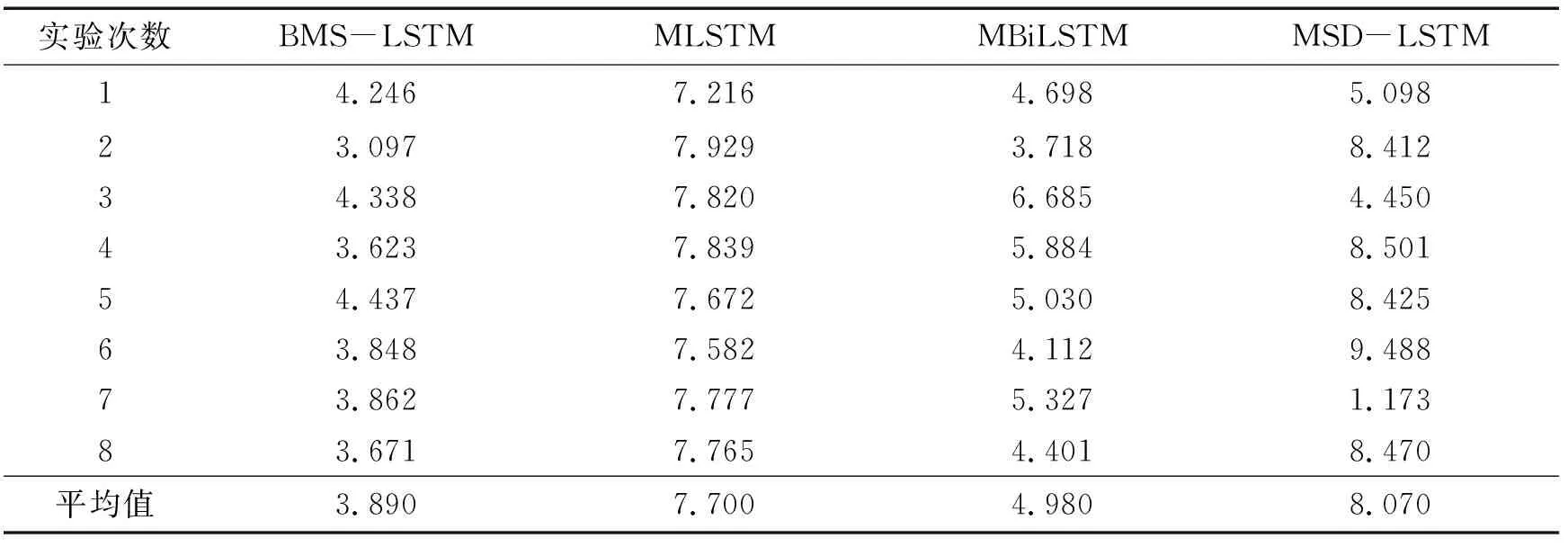
表1 各模型温度预测的平均绝对误差对比

图4直观展示了MLSTM、MBiLSTM、MSD-LSTM和BMS-LSTM这4种模型的预测值与真实值之间的对比结果,从图4可以看出BMS-LSTM与真实值最为接近,预测精度最高,平均误差仅为3.097.

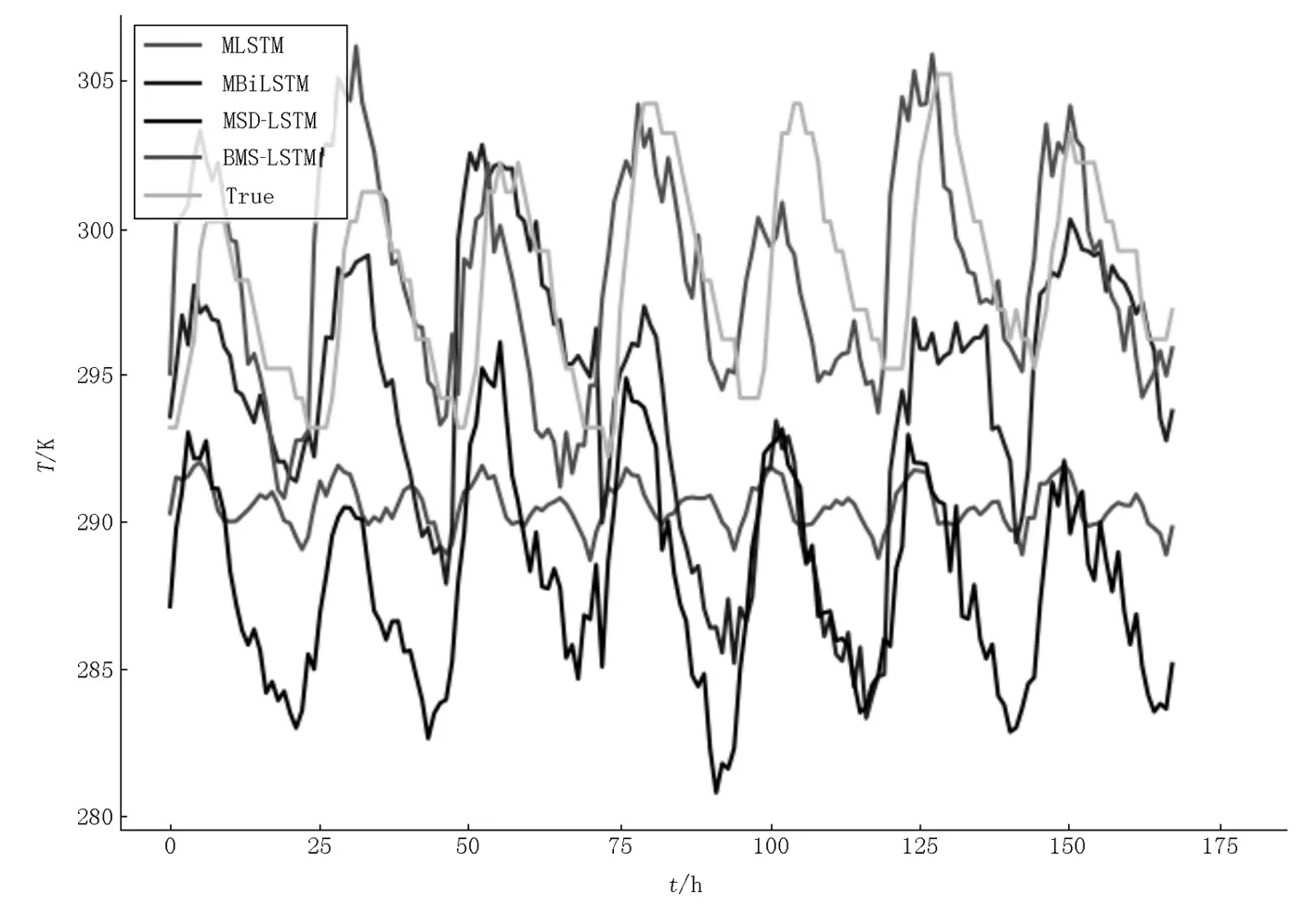
图4 各模型预测结果对比

3.4 超参数探究

为研究层数、跳跃连接数以及神经单元数量对BMS-LSTM性能的影响,本文设置了4组使用不同超参数的对比实验,5次实验结果如表2所示.对比实验1和实验2,可以发现实验2误差较低,这说明合理地增加神经单元的数量有利于提升短期温度预测的精度;对比实验3和实验4可以得到同样的结果.进一步,将实验1、实验2和实验3、实验4进行对比,在神经单元数量相同的情况下,实验3和实验4的误差更低,这表明跳跃连接数影响模型的性能,根据数据实际的多尺度时间结构来选择合适的跳跃数尤为关键.综上所述,在实验4选取的超参数下短期温度预测的精确度最高.因此,高效地使用BMS-LSTM需要综合考虑多个超参数对模型的影响.

表2 不同超参数的预测的平均绝对误差对比

4 结语

近年来,关于循环神经网络提取序列数据的多尺度特征的研究,成果显著,但是依然存在如下缺陷:(i)忽视了数据的反向特征;(ii)跳跃连接数不利于深层网络.这2个缺陷使普通多尺度循环神经网络不适用于短时温度预测.因此,本文提出了BMS-LSTM短期温度预测模型,它使用双向深层网络架构,提取反向特征,设置多个日周期跳跃连接数提取多尺度特征.实验结果表明:BMS-LSTM能有效提取温度数据的多尺度特征和反向特征,提升了预测精度.该模型也存在一定不足,在模型中的跳跃连接数依靠先验知识手动设置,无法自适应的学习时序数据的多尺度特征.如何自适应学习数据的多尺度特征是接下来的研究重点.