用q-差分算子定义的某些解析函数的性质
2022-07-01刘金林
王 波,刘金林
(扬州大学数学科学学院,江苏 扬州 225002)
0 引言
q-微积分由其重要的应用而影响了一些其他学科领域的发展,许多学者在这方面上做了大量研究.F.H. Jackson[1-2]引入并研究了q-导数和q-积分,H.M. Srivastava[3]在几何函数理论中利用q-微积分引入q-超几何函数,G. Gasper等[4]研究并定义了基本超几何级数.最近,一些学者[5-16]研究了用算子定义的解析函数的性质.在上述研究的基础上,本文利用q-差分算子和Janowski函数[17]定义多叶解析函数的一个新子类,给出类中函数的充分必要条件、系数估计、偏差定理、增长定理、凸性半径、星形性半径等几何性质.
1 预备知识
设Ap表示在单位圆D={z∈C:|z|<1}内解析且形如
的函数构成的函数类.特别地,当p=1时,记A=A1.
设f(z)和g(z)在单位圆D内解析,若存在Schwarz函数w(z),使得g(z)=f(w(z))(z∈D),则称g(z)从属于f(z),记为g(z)f(z).特别地,若f(z)是单叶解析函数,则g(z)f(z)⟺g(0)=f(0),g(D)⊂f(D).
定义1设函数p(z)在D内解析,p(0)=1.若p(z)(1+Az)/(1+Bz)(-1≤B 定义2设q∈(0,1),定义q-数如下: 特别地,当λ=0时,记[0]q=0. 定义3设q∈(0,1),f′(0)存在,定义q-差分算子 从定义3可以看出 其中[p]q=(1-qp)/(1-q)=1+q+q2+…+qp-1. 定义4设f(z)∈Ap,-1≤B 则称f(z)∈Sp,q(α,A,B). 由定义4可得如下等价关系: ([p]q[p-1]qf(z)))|<1. (1) 特别地,当参数α、A、B、q、p取特定值时,Sp,q(α,A,B)分别为4个已知重要函数类: (iv)当α=0,A=1,B=-1,q→1-,p=1时,f(z)∈S*,S*表示单叶星形函数类. (2) 证假设不等式(2)成立,要使f(z)∈Sp,q(α,A,B),只需不等式(1)成立.由于 从而f(z)∈Sp,q(α,A,B). 反之,若f(z)∈Sp,q(α,A,B),由定义4知,f(z)满足不等式(1),即 (3) 因为不等式(3)对所有的z∈D均成立,所以令z=Rez→1-可得不等式(2). 综上所述,定理1得证. 由定理1得到如下系数估计. |ap+n|≤(1-α)(A-B)[p]q[p-1]q/((1+B)[p+n]q(α[p+n-1]q-[p-1]q)+(1-α)(1+A)[p]q[p-1]q)(n=1,2,…). 结果是精确的,极值函数为 f(z)=zp-(1-α)(A-B)[p]q[p-1]qzp+n/ ((1+B)[p+n]q(α[p+n-1]q-[p-1]q)+(1-α)(1+A)[p]q[p-1]q). [p]qrp-1-τ1rp≤|∂qf(z)|≤[p]qrp-1+τ1rp, 其中τ1=(1-α)(A-B)[p]q[p-1]q[p+1]q/ ((1+B)[p+1]q(α[p]q-[p-1]q)+(1-α)(1+A)[p]q[p-1]q).结果是精确的,极值函数为 f(z)=zp-(1-α)(A-B)[p]q[p-1]qzp+1/ ((1+B)[p+1]q(α[p]q-[p-1]q)+(1-α)(1+A)[p]q[p-1]q). 因为|z|=r<1,所以rp+n-1≤rp,故 (4) 同理可得 (5) 因为f(z)∈Sp,q(α,A,B),所以,由定理1得 从而 因此 从而 (6) 将式(6)代入式(4)和式(5),定理2得证. 利用定理2的证明方法可以得到如下增长定理. rp-τ2rp+1≤|f(z)|≤rp+τ2rp+1, 其中τ2=(1-α)(A-B)[p]q[p-1]q/((1+B)·[p+1]q(α[p]q-[p-1]q)+(1-α)(1+A)·[p]q[p-1]q).结果是精确的,极值函数为 f(z)=zp-(1-α)(A-B)[p]q[p-1]qzp+1/ ((1+B)[p+1]q(α[p]q-[p-1]q)+(1-α)·(1+A)[p]q[p-1]q). 有f(z)∈Cp(σ). 证设f(z)∈Sp,q(α,A,B),要使f(z)∈Cp(σ),只需 (1+zf″(z)/f′(z)-σ)/(p-σ)(1+z)/(1-z),0≤σ 上式等价于|(zf″(z)-(p-1)f′(z))/(zf″(z)+(1-2σ+p)f′(z))|<1,化简后得 (7) 由不等式(2)得 因此,若不等式(7)成立,则只需 即 |z|n 也就是 |z|<(p(p-σ)((1+B)[p+n]q(α[p+n-1]q-[p-1]q)+(1-α)(1+A)[p]q[p-1]q)/((p+n)(n+p-σ)(1-α)(A-B)[p]q·[p-1]q))1/n. 定理4得证. 利用定理4的证明方法可得到在Sp,q(α,A,B)中函数的星形性半径. q-微积分在经典的几何函数论中有着广泛应用,如通过q-微积分研究q-超几何函数级数.本文利用q-差分算子和Janowski函数引入多叶解析函数的一个新子类,通过给出该类子族解析函数的充分必要条件,得到了该类子族的系数估计、偏差定理、增长定理和星形半径等几何性质.




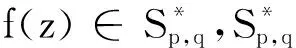

2 主要结果
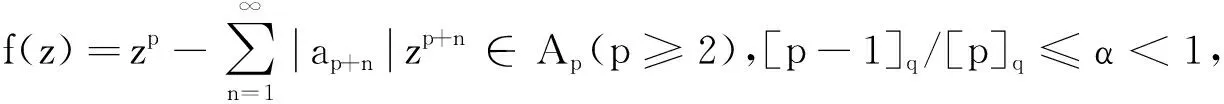





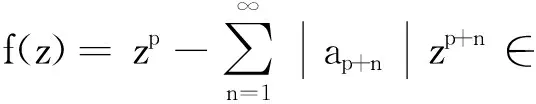






3 结束语
