SAV方法求解Allen-Cahn方程的数值比较
2022-07-01翁智峰
陈 航,吴 哲,翁智峰
(华侨大学数学科学学院,福建 泉州 362021)
0 引言
S.M. Allen等[1]提出反相边界运动的微观理论,对应的Allen-Cahn方程在描述相场变化上有着非常广泛的应用,如研究生物种群之间的竞争和排斥[2]、在已知温度气压下晶体的生长[3]、河床的迁移[4]、在材料学中界面扩散动力学[5]等.
本文考虑能量泛函
(1)
其中F(u)=(u2-1)2/(4ε2)为双位势阱函数,则可以写出式(1)对应的梯度流方程(即Allen-Cahn方程)
ut=-Mμ,μ=-Δu+F′(u),(x,t)∈Ω×(0,T],u0=u(x,0),x∈Ω,u|∂Ω=0,
(2)
其中M为迁移率系数.
近年来,许多学者对Allen-Cahn方程的数值解进行了深入广泛研究,主要包括有限差分法[6]、有限元法[7]、谱方法[8]等.如D.J. Eyre[9]提出了唯一解且无条件能量稳定的凸分裂方法;Chen Longqing等[10]构造了满足能量稳定的1阶精度和2阶精度的半隐格式;Choi Jeongwhan等[11]提出了一种求解Allen-Cahn无条件梯度稳定的数值格式,可以满足能量耗散;Yang Xiaofeng等[12]提出了不变能量2次化(IEQ)的方法来求解分子束外延生长模型,只要满足非线性项有下界,就可以保证修正的能量稳定;Shen Jie等[13]提出了标量辅助变量(Scalar Auxiliary Variable,SAV)方法求解梯度流问题,该方法只要非线性项F(u)的积分项有下界条件,就可以保证修正的能量无条件稳定.SAV方法保留了不变能量2次化的优点,也不需要每一步求解变系数方程,只需每一步求解常系数的线性方程组,并且在差分格式下对应的常系数方程组有快速方法进行求解,数值格式非常高效.由于SAV数值格式的诸多优点,所以它被广泛应用于求解各类微分方程,如Allen-Cahn方程和Cahn-Hilliard方程[14]、研究细菌趋化性的Keller-Segel方程[15]、在流体力学中的Navier-Stokes方程[16]等.
众所周知,在Lagrange插值公式描述经过插值点的近似函数时,若节点过多则会产生Runge现象,而N.J. Higham提出的重心型Lagrange插值[17]解决了该问题,并且若将节点改成Chebyshev节点则可以使插值达到很高的精度.重心插值配点法[18]作为一种新型的无网格计算方法,能有效地避免差分格式带来的累积误差,使用Chebyshev节点有效地克服了Runge现象,且其具备计算格式简单、精度高、程序实施方便、节点适应性好等特点.如今,已经应用在求解各类微分方程(如分数阶Fredholm积分方程[19]、平面弹性问题[20]、Allen-Cahn方程[21]等)中.
本文主要利用SAV格式结合无网格型的重心Lagrange插值配点法来求解Allen-Cahn方程.首先,基于SAV数值格式的Allen-Cahn方程,在空间方向上采用了高精度的重心Lagrange插值格式,并与常见的2阶中心差分格式做比较,观察2者误差和收敛阶;然后,再利用差分矩阵的性质,运用离散正弦变换(Discrete Sine Transform,DST)求解2阶中心差分导出的线性方程组和快速傅里叶变换(Fast Fourier Transform,FFT)计算Toeplitz矩阵与向量的乘积;最后,验证重心Lagrange插值配点数值格式指数收敛且耗时少.
1 Allen-Cahn方程的无条件能量稳定格式
1.1 Allen-Cahn方程的SAV形式
ut=-Mμ,
(3)
(4)
(5)
进而,只需对式(3)内积μ,式(4)内积ut,式(5)乘以2r,整理即可得到

(6)
所以式(6)对应修正的能量泛函E(u)=(u,-Δu)/2+r2是无条件能量稳定的.
1.2 时间方向的2种离散格式
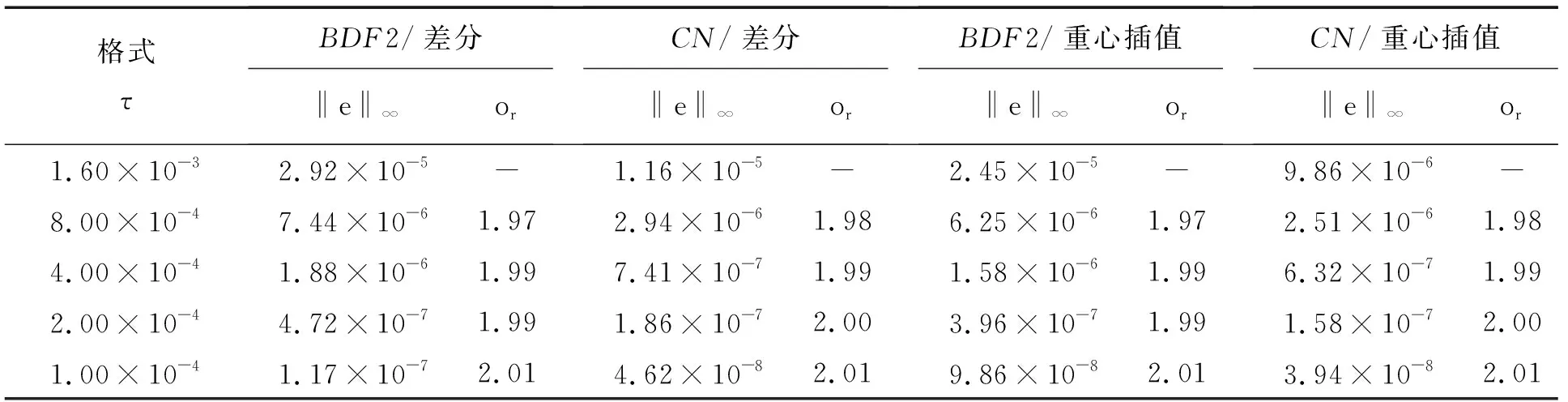
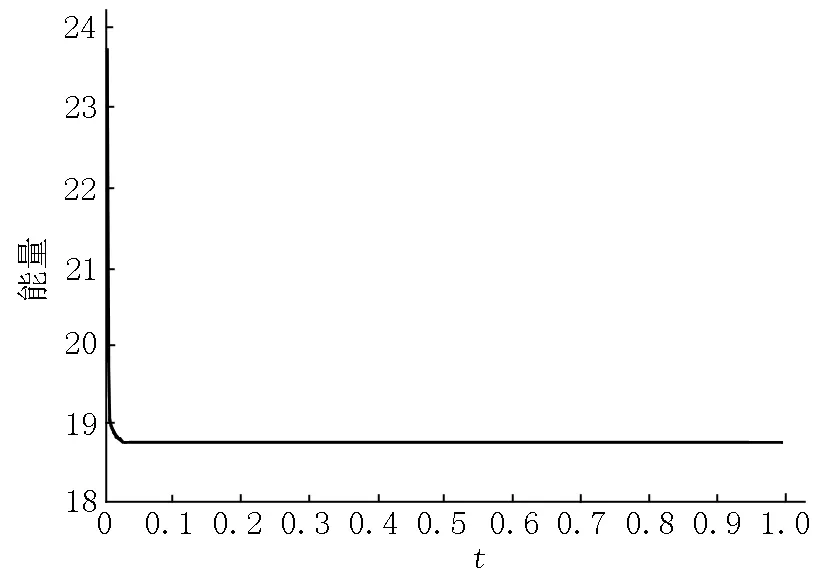
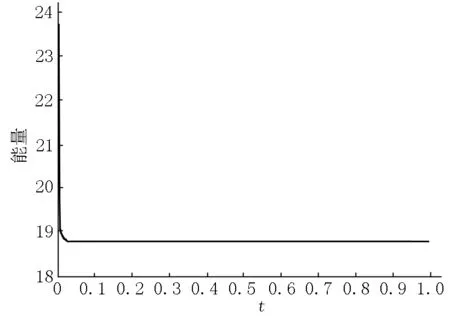
对方程的时间偏导数部分,采用2阶向后差分(BDF2)格式和Crank-Nicolson(CN)格式进行离散.记在[0,T]上的离散点为0=t0 1.2.1 2阶向后差分格式 利用BDF2格式,取正整数N,记τ=T/N,tn=nτ(0≤n≤N),给出半离散格式: (3un+1-4un+un-1)/(2τ)=-Mμn+1, (7) (8) (9) 满足E(un+1,un)≤E(un,un-1). 1.2.2 Crank-Nicolson格式 利用CN格式,取正整数N,记τ=T/N,tn=nτ(0≤n≤N),给出半离散格式 (un+1-un)/τ=-Mμn+1/2, (10) (11) (12) 满足E(un+1)≤E(un). 对方程的空间2阶偏导数部分,采用2阶中心差分离散和重心Lagrange插值配点法进行离散.记在[a,b]上m等分后的离散点为a 从而可以得到2阶空间离散Δun.其中容易证明Δ是对称负定矩阵,且该空间离散的收敛阶是2阶的.由于对称负定矩阵的特殊性质,所以可以用快速算法计算在迭代过程中的线性方程组的解和矩阵向量的乘积部分,具体步骤将在后面的计算过程中给出. 1.3.2 重心Lagrange插值配点法 为了得到更高收敛阶的空间离散格式,采用重心Lagrange插值配点法离散空间,并与2阶中心差分格式离散空间进行比较.对于在区间[a,b]上的离散点,函数u(x)在节点xj处的函数值为uj=u(xj),则可以写出u(x)的重心型插值函数 (13) 记重心Lagrange插值的微分矩阵为D,利用插值函数(13)可以写出在插值节点处的导数 通过对Lj(x)求导,再利用数学归纳法则可以得到D(p)的递推公式 从而可以得到2阶微分矩阵D(2),即Δu=D(2)u. 由于重心Lagrange插值对于Chebyshev节点有较高的数值稳定性,所以本文将选用第2类Chebyshev节点及其重心插值权,其计算公式如下: xj=cos(jπ/n),j=0,1,2,…,m, 从而利用Chebyshev节点作为Lagrange插值配点,对应地就可以给出下面的插值逼近性质. 定理1[22]若u(x,t) 在[a,b]×(0,T]上连续,且边界是Lipschitz连续.记h=(b-a)/2,则存在常数c0、c1有误差估计如下: 由定理1可知,重心Lagrange插值配点法是指数收敛的. (I/τ-2MΔ/3)un+1+Mβn+1(βn+1,un+1)/3=(4un-un-1)/(3τ)-2Mβn+1(4rn-rn-1-(βn+1,4un-un-1)/2)/9=Qn, (14) 令A=I/τ-2MΔ/3,对于中心差分格式离散空间方向,矩阵A显然是三对角对称可逆矩阵.则可对式(14)先左乘A-1,再内积βn+1,得到 (βn+1,un+1)=(βn+1,A-1Qn)/(1+M(βn+1,A-1·βn+1)/3)=α. 最后计算 un+1=A-1Qn-MA-1βn+1α/3,rn+1=(4rn-rn-1)/3+(βn+1,3un+1-4un+un-1)/6, (I/τ-MΔ/2)un+1+Mβn+1/2(βn+1/2,un+1)=(I/τ+MΔ/2)un-Mβn+1/2(2rn-(βn+1/2,un))=Qn. (15) 令A=I/τ-MΔ/2,因为A是三对角对称可逆矩阵,所以同理可对式(15)先左乘A-1,再内积βn+1/2,得到 (βn+1/2,un+1)=(βn+1/2,A-1Qn)/(1+M(βn+1/2,A-1βn+1/2))=α. 最后计算 un+1=A-1Qn-MA-1βn+1/2α,rn+1=rn+(βn+1/2,un+1-un), 这2种格式在计算的过程中都需要用到前2步的信息,可以先采用1阶格式,类似上述步骤利用u0求出u1,再进行迭代. 1.4.2 离散正弦变换和快速傅里叶变换 为了用快速算法求解导出的线性方程组,先介绍特殊矩阵的性质,有如下2个引理. 引理1[23]对于m×m的三对角矩阵T=tridiag(a,b,c),它的m个特征值为 则可将T分解为T=PΛP-1=Pdiag(λ1,λ2,…,λm)P-1,特征值λk对应的特征向量为Pk,其中第j个分量为 Pkj=(a/c)j/2sin(jkπ/(m+1))(j=1,2,…,m). 引理2[23]对于m×m的循环矩阵C=circle(a0,a1,…,am-1),它的m个特征值为 ωk=cos(2kπ/m)+jsin(2kπ/m)=e2kjπ/m(0≤k≤m-1), 则可将C分解为C=FΛF-1=Fdiag(g(ω0),g(ω1),…,g(ωm-1))F-1,特征值g(ωk)对应的特征向量Fk为 由于空间采用2阶中心差分离散,且A是三对角对称Toeplitz可逆矩阵,所以可以利用离散正弦变换(DST)快速计算Ab,A-1b. 先利用引理1计算出A的特征值,令A=PΛP-1.由DST和IDST的性质[23]知 由矩阵A的特征可知,Ab、A-1b可以用DST和IDST快速计算,即 A-1b=PΛ-1P-1b=fDST(Λ-1fIDST(b)), Ab=PΛP-1b=fDST(ΛfIDST(b)). 将Toeplitz矩阵T扩充成循环矩阵 再利用离散傅里叶变换(DFT)性质知 最后取所得向量的前半部分即可. 选取u(x,0)=u0=0.5sin(πx),(x,t)∈[-1,1]×[0,1],取M=1,ε=0.1.由于没有准确值,所以取τ=1×10-5,使计算出的un作为参考解u(tn),则计算最后时刻T的误差e=|un-u(tn)|,收敛阶 or=log2(ei+1/ei)/log2(τi+1/τi) 取空间离散点数m=16,计算时间收敛阶如表1所示. 表1 在m=16时的L∞误差和时间收敛阶 从计算结果可以看出,BDF2格式和CN格式的收敛阶都是2阶的(见图1和图2).在相同空间离散格式下,CN格式的精度比BDF2格式的精度高. 图1 BDF2格式收敛阶 图2 CN格式收敛阶 考虑空间离散方式不一样,假设真解u(x,t)=costsin(πx),代入Allen-Cahn方程中计算得到函数 g(x,t)=sin(πx)(-sint+Mπ2cost+Mcost·((costsin(πx))2-1)/ε2), 取τ=1×10-5,M=1,ε2=0.1,计算结果如表2所示. 由上述分析结果可以看出,空间离散使用中心差分的收敛阶是2阶的.重心Lagrange插值配点法可以在较小的剖分中得到较高的精度,收敛阶是指数递减的.在相同的时间离散格式下,重心Lagrange插值配点法的精度比2阶中心差分格式的精度高很多,前者只需要6个节点就可以达到后者32个节点的精度,前者在10个节点时的误差就远小于后者在128个节点时的误差. 接下来讨论BDF2格式和CN格式的运行时间,运行环境为8G(intel)i5-7200U.选取N=104,对于差分离散,选取空间剖分数m=210.因为由上述实验可知,重心Lagrange插值配点法的计算结果的误差较小,所以对于重心Lagrange插值配点法离散选取m=10.由上述实验可知重心Lagrange插值配点法的误差较小,下面比较常规计算和快速计算以及重心Lagrange插值配点法离散的运行时间(见表3). 表3 不同格式的CPU计算时间 由表3可以很明显看出,快速算法对差分格式的计算时间有较大提升,而重心Lagrange插值配点法能经过很少节点就达到高精度从而缩短了计算时间. 取u0=sin(πx),(x,t)∈[-1,1]×[0,1]取M=1,ε=0.1,m=210,τ=1×10-4,1维等距剖分的能量离散形式为 由图3和图4可见:在空间是2阶中心差分离散空间的情况下,时间离散的BDF2格式和CN格式都满足能量耗散,且到达稳定的时间几乎一致. 图3 BDF2/差分格式 图4 CN/差分格式 取u0=sin(πx),(x,t)∈[-1,1]×[0,1],M=1,ε=0.1,m=12,τ=1×10-4,在Chebyshev节点下的能量离散形式为 同样,对于重心Lagrange插值配点法空间的情况,时间离散的BDF2格式和CN格式都满足能量耗散.如图5和图6所示,BDF2格式在t=0.6之前达到稳定,而CN格式在t=0.6后达到稳定,这说明对于同种情况下,CN格式需要更多时间才达到能量稳定. 图5 BDF2/重心插值格式 图6 CN/重心插值格式 本文利用重心Lagrange插值配点法结合SAV格式来求解Allen-Cahn方程,对比了几种离散格式的精度和能量耗散情况.通过算例可以发现:在同种空间离散格式下,CN格式的精度比BDF2格式更高;在同种时间离散格式下,重心Lagrange插值配点格式的精度比2阶中心差分的精度更高,且收敛阶是指数收敛.虽然DST和FFT快速算法结合2阶中心差分格式求解所用的CPU时间变少,但是重心Lagrange插值配点法求解所用的CPU时间仍然比快速算法的差分格式求解所用的CPU时间更少.进一步地,数值算例验证在SAV方法下的几种数值格式都满足能量耗散规律.

1.3 空间方向的2种离散格式


1.4 SAV方法计算步骤和技巧


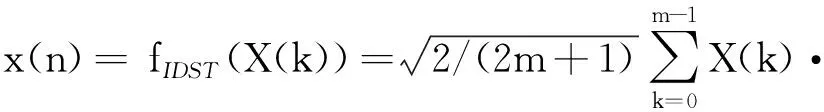
2 数值实验
2.1 算例1



2.2 算例2



3 结束语
