大跨度异形拱桥全桥受力行为及稳定性分析

2022-07-01姜徐磊李维华郭小平黄贤增张明金

广东土木与建筑 2022年6期

姜徐磊，李维华，郭小平，黄贤增，骆鹏，张明金

（1、西南交通大学土木工程学院成都 610036；2、中国瑞林工程技术股份有限公司南昌 330038）

0 引言

随着社会的快速发展，桥梁除了满足交通运输的要求之外，越来越重视美学观念与艺术价值。异形拱桥形状独特、曲直结合，是近些年来新兴的一种桥型。2005 年建成的天津市大沽桥采用不对称联合梁系杆拱桥，由两个不对称的拱圈构成，两个拱圈大小和外倾角度均不同，极富有创新性。诸多学者也对异形拱桥的受力特性展开研究：陈宝林等人［1］通过有限元软件对大跨度异型拱桥建模，对关键截面处的挠度及应变测点布置进行设计并对相应测试结果进行分析。王永等人［2］阐述了梁肋斜交空间曲面吊索异形拱桥设计的关键技术。张伟等人［3］分析了拱肋外倾角度、刚度及其与横撑交点位置等参数对异形拱桥稳定性以及自振特性的影响。陈得意等人［4］结合马尔科夫理论和异形拱桥拱肋施工过程的特点，首次建立了针对异形拱肋空间线形精确预测的考虑残差的马尔科夫模型，导出了弱化随机误差以后的异形拱肋空间坐标计算表达式。孙全胜等人［5］研究了异形斜杆三连拱桥主梁及拱肋在不同结构参数下对主梁位移、主拱肋轴力、吊杆索力等的影响，证明了主拱肋外倾角度选择的合理性。异形斜拉拱桥由于构件的布置方式使其受力具有空间性，属于空间超静定结构，拱肋往往在受压受弯的同时还会产生抗扭转的力，压弯扭耦合效应对拱肋的影响显著；而且拱肋的异化对于整体结构的稳定性往往有较大影响，拱肋受力后变形大，拱顶处的横向位移突出，横向稳定性差；斜向吊索力在吊索锚固处对拱肋和主梁均会产生轴力突变现象［6-7］。本文利用有限元分析软件Midas Civil 并结合相关规范对大跨度异形斜拉拱桥成桥状态的力学行为进行分析研究。

1 工程概况

某大跨度异形拱桥位于某市市区，主跨为（60+135+135+60）m，全长390 m，中间桥塔区吊杆共6 根，非桥塔区吊杆共22对，平均分布在桥塔两侧。桥面为双线6车辆公路，采用多纵梁正交异性钢桥面方案，纵梁采用四根钢箱梁，梁高3.0 m，每两根钢箱梁之间布置一根倒T 型梁，梁高1.8 m。桥面宽度为50 m，分为拱塔区、车行道区、非机动车道区、吊杆区以及人行道区。本大桥立面及横断面布置如图1所示。

图1 大桥立面及横断面布置Fig.1 Elevation and Cross-sectional View of the Bridge

2 有限元建模

依据设计资料采用Midas Civil 有限元分析软件建立全桥模型，对其受力特性进行计算分析。该方法能较真实地模拟全桥的整体刚度和受力行为，同时减少计算工作量，兼顾计算精度和效率。全桥有限元模型以理论竖曲线为基准进行结构离散，主梁和拱肋主要受弯矩作用，采用梁单元，共2 708 个，吊杆主要受轴力作用，采用桁架单元，共50个，最终共有空间单元2 758个；全桥空间几何模型如图2所示。

图2 全桥空间几何模型Fig.2 Spatial Geometry Model of the Bridge

主梁和拱肋均采用Q345qC钢材，下拱采用C40混凝土，两端吊杆（共22对）内的斜拉索采用37ϕ15.2钢绞线，桥塔处吊杆（共6根）内的斜拉索采用15ϕ15.2钢绞线，不同材料的物理性能如表1所示。

表1 材料物理性能指标Tab.1 Material Physical Performance Index

3 计算荷载及工况

3.1 计算荷载

纵梁每延米平均重量为170 kN∕m，外横梁总计重量为2 285.7 kN，箱间横梁总计重14 939.2 kN。上拱总计重613.4 kN，吊杆总计重913.6 kN。二期恒载每延米平均重量为84.9 kN∕m。

全幅桥车辆按六车道计算，汽车荷载采用城-A级并计入冲击、车道折减等影响。冲击系数按照《公路桥涵设计通用规范：JTG D60—2015》［8］取0.05，车道横向折减系数取0.5，纵向折减系数取0.97，同向行驶三车道的汽车荷载制动力标准值应为一个设计车道制动力标准值的2.34倍，人群荷载标准值取3.5 kN∕m2。

体系整体升温为35 ℃，整体降温为-25 ℃。体系竖向日照正温差计算的温度基数T1=25 ℃，T2=6.7 ℃，竖向日照负温差为正温差乘以-0.5。

根据《公路桥梁抗风设计规范：JTG∕T 3360-01—2018》［9］，桥位处百年一遇的基本风速为U100=27.1 m∕s，十年一遇的基本风速为U10=22.7 m∕s，该地区所对应的风险区域为R2，抗风风险系数为kf=1.02，地形条件系数取为kt=1.0，故可求得主梁高度处百年一遇的风荷载为2 654 N∕m，十年一遇的风荷载为1 897 N∕m。

3.2 工况设置

按照承载能力极限状态和正常使用极限状态分为两大类工况。承载能力极限状态验算下的荷载组合有4种，包括工况1～工况4；正常使用极限状态验算下的荷载组合有3 种，包括工况5～工况7。同时设置仅有恒载作用的工况进行对照，恒载作用包括结构重力、预加力、收缩徐变、基础变位作用等。各类工况下的荷载组合如表2所示。

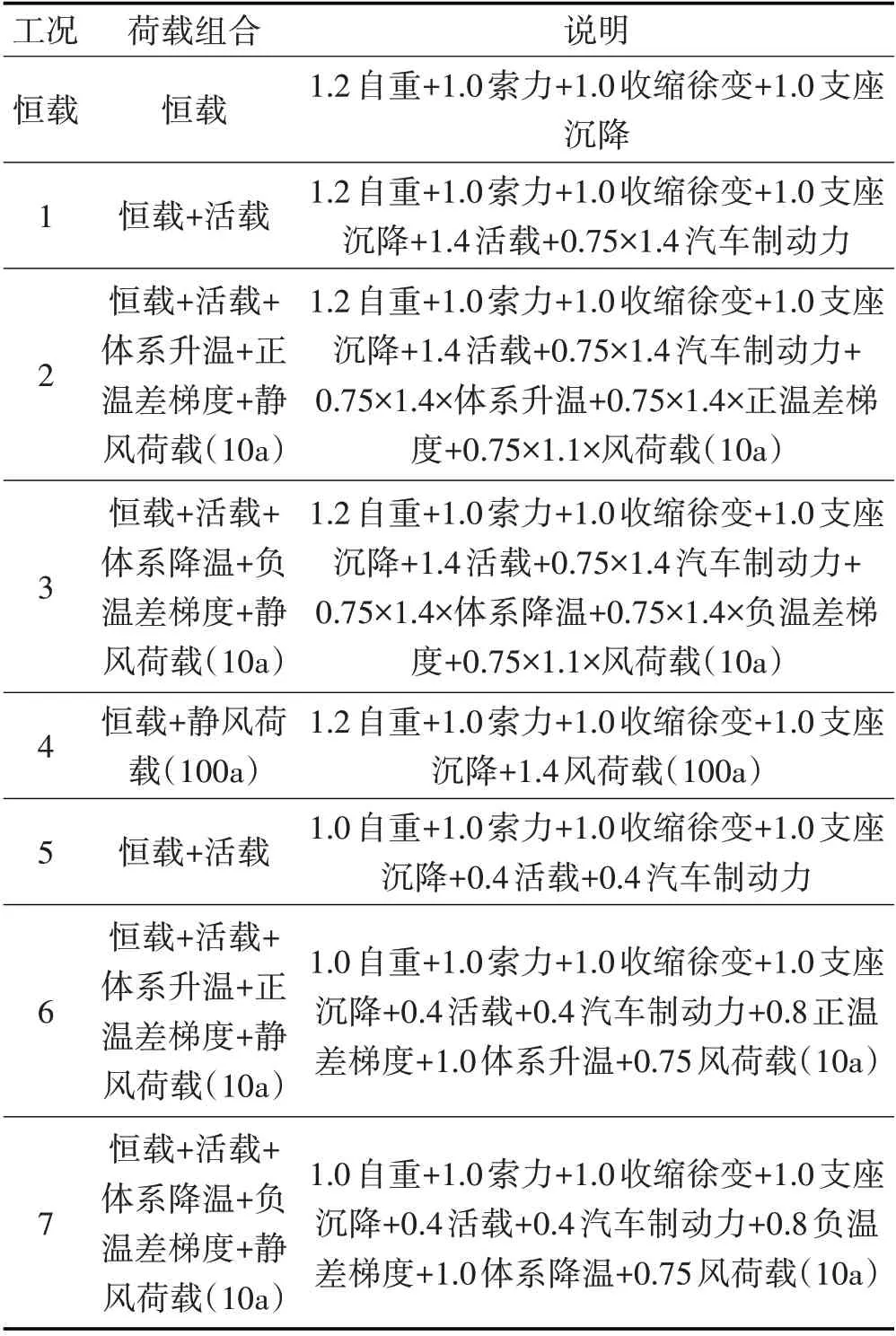
表2 工况中荷载组合Tab.2 Load Combination in Different Cases

4 结果分析

根据该大桥的结构特征，重点分析了主要受力部位的应力分布特征，全桥结构的刚度分析以及全桥稳定性分析。

4.1 应力分析

成桥阶段除了要考虑主梁和上拱的应力状态外，跨中支座附近横梁往往也会承受很大的应力，出于安全考虑，将跨中支座附近横梁一并进行应力分析。主梁、横梁和上拱部位在不同工况下的最大弯曲应力如图3所示。可知，在承载能力极限状态下，出现最大弯曲应力的位置位于工况3 中的横梁部位，大小为238.2 MPa，并且除了工况4之外，横梁的最大弯曲应力都大于主梁与上拱的最大弯曲应力。虽然最大弯曲应力值未超过结构钢材的抗弯强度设计值285 MPa，但在结构设计时有必要考虑跨中横梁的可靠性。在正常使用极限状态下，出现最大弯曲应力的位置位于工况6中的上拱部位，大小为171.8 MPa，结构钢材存在一定的安全余量，保证结构正常使用。主梁的最大正应力多出现在外箱梁上边缘，最大负应力多出现在倒T 型梁下边缘；上拱的最大负应力多出现在拱圈交点附近。

图3 不同工况下最大弯曲应力Fig.3 Maximum Bending Stress in Different Cases

成桥阶段正常使用极限状态下吊杆应力的计算结果如表3所示，由于结构对称，且桥塔处吊杆的应力值相对较小，仅展示各个工况下1#～11#吊杆的应力结果，如图4 所示。从表3 和图4 可知，出现最大正应力的部位位于工况2中的11#吊杆，大小为591.5 MPa；每个工况下1#～11#吊杆的应力最大值都呈现出向上开口的抛物线趋势，即先减小后增大，并且吊杆的应力峰值多出现在拱脚附近的吊杆上；除了桥塔区的吊杆外，拱肋下吊杆的安全系数都介于3～6 之间，在保证结构安全使用的同时也避免了材料浪费。

表3 吊杆应力计算结果Tab.3 Results of Suspender Stress

图4 1#～11#吊杆应力最大值Fig.4 Maximum Stress of 11 Suspenders

4.2 刚度分析

成桥阶段在不同荷载作用下主梁与拱肋发生的竖向最大位移如图5 所示。由图5 可知，由活载作用引起的主梁与拱肋部位的下挠值在所有工况中最大，主梁的竖向最大位移是48.4 mm，方向向下，拱肋的竖向最大位移是37.3 mm，方向向下；主梁与拱肋的竖向位移都主要由活载作用控制。温度作用方面，体系整体温度变化与温度梯度皆会引起桥梁结构一定程度的竖向位移，体系整体温度变化所引起的竖向位移值要大于由温度梯度所引起的竖向位移值；整体升温与升温梯度所引起的竖向位移值都为向上拱起，而整体降温与降温梯度所引起的竖向位移值都为向下凹陷。风荷载无论是十年一遇还是百年一遇都属于横向施加的作用，并且钢桥本身刚度很大，于是对结构竖向位移的作用不是很大，因此风荷载所引起的下挠值在所有工况中最小。

图5 不同荷载作用下构件竖向最大位移Fig.5 Maximum Vertical Displacement of Components under Different Loads

4.3 稳定性分析

对于拱肋结构而言，大致可分为两类稳定问题：对于一般的拱桥结构，其受力以面内为主，面内失稳以极值点为主，即第一类稳定问题；对于即可能发生面内失稳又可能发生面外失稳的为空间失稳，空间失稳主要以分支点为主，即第二类稳定问题。对于复杂桥梁的稳定性问题目前一般采用有限元理论进行分析，主要有线性屈曲和非线性屈曲两种。虽然线弹性法没有考虑结构的几何非线性和材料非线性，但是由于其概念清晰，计算简便，本算例中仍然采用线弹性方法分析其稳定性［10］。

根据线弹性理论，结构在外荷载作用下的平衡方程为：

式中：K0为结构弹性刚度矩阵；Kg为几何刚度矩阵；λ为结构的稳定系数；δ为节点位移增量。

该平衡方程即为特征值问题，λ也为失稳特征值。在自重和二期恒载作用下，该大桥前4 阶模态的失稳特征值如表4 所示，前4 阶的失稳模态如图6 所示。由表4可知，该大桥的第1阶模态失稳特征值（即屈曲安全系数）为10.9，失稳模态为面外反对称失稳，第2～4 阶的失稳模态皆为面外正对称失稳，可见当桥梁结构刚度很大时，失稳特征值比较大，结构发生失稳破坏时的概率越低。