热压作用下街区峡谷内通风模拟

赵福云 刘宝 成瑾 黄志荣 文雅冰 唐宇飞

湖南工业大学土木工程学院

据联合国环境规划署统计，在全球范围内，每年室外空气污染可导致420 万人过早死亡，暴露于受污染的空气几乎无法逃脱，据世界卫生组织统计，十分之九的人呼吸的空气超过了安全限制，城市空气质量问题不容忽视。在晴朗无风的天气，往往会形成城市热岛的存在，此时，由于缺乏来流风的影响，城市表面形成的热浮升力成为清除城市内热和污染物的主要动力。Yifan Fan[1]研究了浮力驱动下的城市大气环流，表明从周边农村地区的低水平空气可以改善城市通风并降低城市污染物浓度。Lina Yang[2]测量了无风状态下香港地区山坡与城市建筑之间因为热对流引起的通风，发现由建筑产生的热浮升力在城市通风潜力中尤为重要。以往的城市通风文献中，几个因素被确认为在城市街道通风中影响很大，其中街道纵横比是已被证明的最重要的因素之一，特别是在二维街道峡谷中，不同的街道纵横比将流场分成了四个不同的区域[3-5]。其他的影响因素还包括城市填充密度[6]，建筑形态[7]等。但是此类文献大多数是在有风的情况下进行的，单纯就热压情况下对城市街区研究很少，本文以热压为基础，研究了不同建筑群大小及不同高宽比因素对街区通风的情况。

1 三维街区CFD 模型

1.1 物理模型

本次研究的对象是街区建筑之间的通风情况，考虑到现实中建筑围护结构较为复杂，并且对研究对象影响较小，于是将街区中的建筑简化成长宽高均为H，街道宽度为W，街道纵横比为H/W，如图1 所示，本次研究的街区建筑数量为M2，M取值为2 到6，对于计算域的设定，Gan G[8]比较了原本物理尺寸的计算域和扩展后的计算域得出的结果，发现自然通风通风率和壁面传热系数有很大的区别，计算域扩展后的计算结果更贴近实验的结果，本文模拟也选取扩展计算域的方法，其中L=22H。对于边界条件设定，顶部选取symmetry 条件，侧边选取pressure-outlet 条件，建筑群和街道采取恒温且与周围空气温度相差10 K。

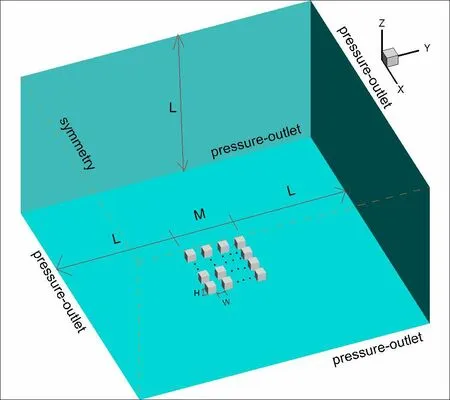
图1 CFD 模型及计算域

1.2 网格及模型验证

利用ICEM 软件进行三维网格划分，为了减少误差采用结构化网格，并对建筑壁面及街道地面进行网格加密，第一层网格设为0.05，网格膨胀因子为1.2，保证了30≤Y+≤150。为了验证本模型的正确性，本文采取对照实验的方式选取了Pham[9]等人利用三维粒子测量技术测量热羽流的实验数据进行对比，结果如图2 所示，对照数据采集的是热源上方竖直方向速度与最大速度之比，可以看出，数据吻合较好。本文比较感兴趣的是街区峡谷内空气质量，所以选择在街区内进行增加/减少网格进行网格独立性验证，取街区内节点数为30×30 为基础网格，并增加1.5 倍、减少1.5 倍制定fine、coarse 两种网格密度，取街区中心位置Z 方向速度进行比较，如图3 所示，在z 方向上，basic 网格与fine 网格产生的速度变化已不大，即basic 网格已基本满足要求。

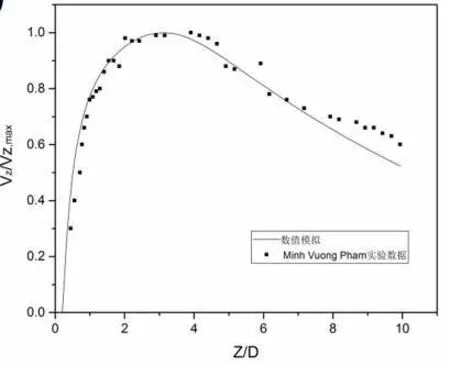
图2 模型验证

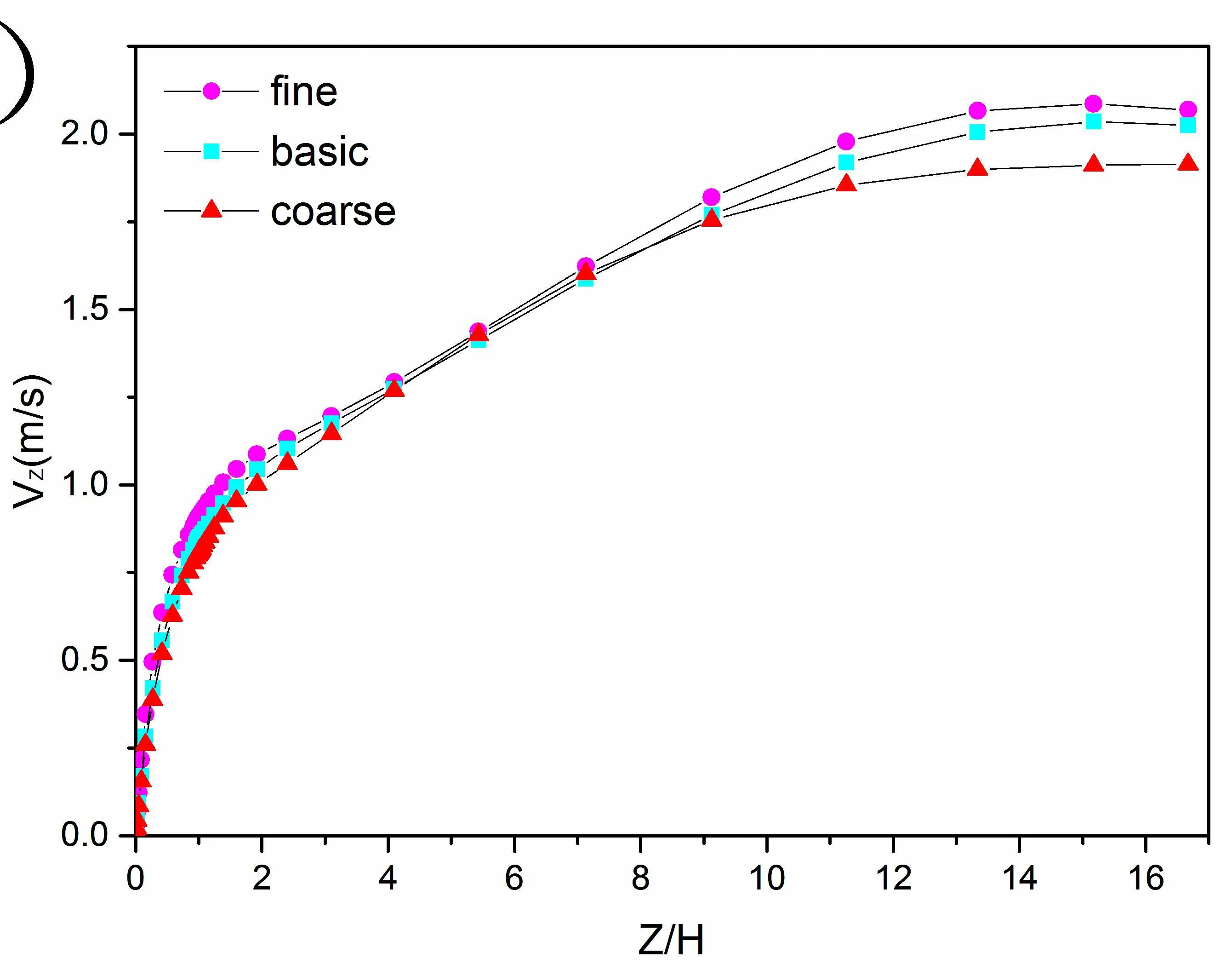
图3 网格独立性验证

1.3 求解步骤

数值仿真采用Anasys 19.0 中的fluent 作为求解器，利用压力基求解器求解连续性方程，动量及能量方程。本模型的Gr 大于2×1010已经处于湍流状态，RNGk-e模型对于湍流处理精度较高且提高了湍流漩涡的可信度，故选用此模型对模型进行求解。采用coupled算法进行迭代计算求解，能量残差收敛标准设为10-6，其他的残差变量均设为10-3。

2 结果分析

2.1 单个街区内温度及速度分析

本次结果取M=5 时的街区进行分析，建筑模型边长H设为30 m，街道宽度W设为30 米，街道纵横比为1。为便于数据对比，对温度和速度进行了无量纲化处理，过程如下：

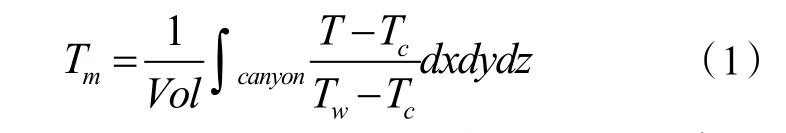
式中：Tm是平均无量纲温度，Tc是环境温度，Tw是建筑表面温度。

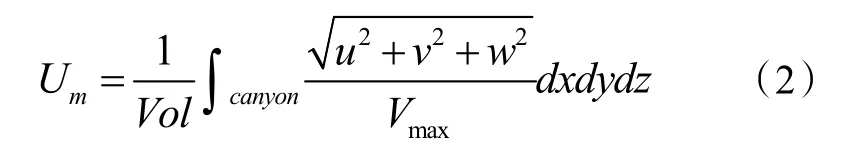
式中：Um是平均无量纲速度，u，v，w分别是速度沿X，Y，Z 轴方向的速度分量，Vmax取街区峡谷冠层平面速度最大值。

如图4 所示为所有街区峡谷的平均无量纲温度和平均无量纲速度分布，从图4a 可以看出建筑壁面热流对峡谷内的空气温度有明显的影响，从建筑群边缘往中心的方向上，温度在不断增加，说明收敛流对建筑边缘街区峡谷内降温较为明显，但是在中心位置确是会抑制热量的散发，建筑群中心街区峡谷出现了较大的温升。相较于温度变化，平均无量纲速度变化则较为平缓，整体上是朝着街区边缘峡谷逐渐减少的趋势（图4b）。

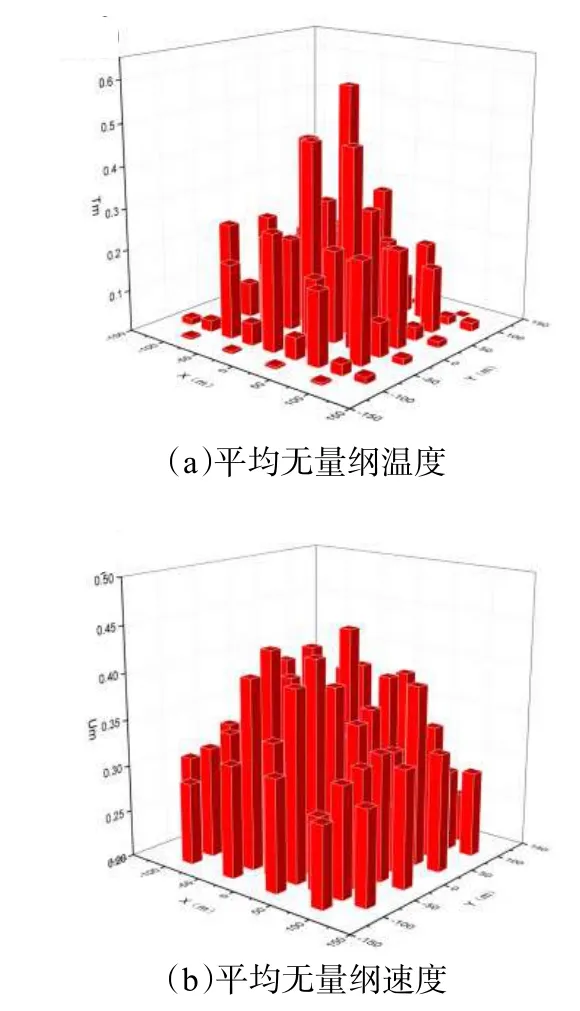
图4 单个街区峡谷内平均无量纲温度与速度

2.2 不同街区的温度及速度分析

本部分主要研究的不同街区大小对街区峡谷内的温度及速度的影响，街区大小M的变化范围是2 到6。图5 给出了不同街区行人层（Z=2 m）无量纲温度分布，云图中的温度分布表明了随着街区的增大，街区中心峡谷内温升越来越明显，而街区边缘峡谷内温升较小，主要原因是收敛流产生的降温效果且随着建筑群的增大降温效果更加明显。从图6a（图中右上角标注区域为所选街区峡谷）中可以看出，随着街区的增大，总体的平均无量纲温度随之增加，且街区边缘峡谷内温升较小，在街区中心峡谷内温升较大，最大处温升达到0.65 ℃。平均无量纲速度整体趋势也是随着街区的增大而变大，从街区边缘往中心的方向上，平均无量纲速度不断增加，在街区中心峡谷内却出现了减小的情况。造成此种结果的原因是由于压差使周围的收敛流空气不断加速，故气流速度不断增大，但是在街区中心峡谷内方向相反的两股气流会出现抑制作用（图6b）。

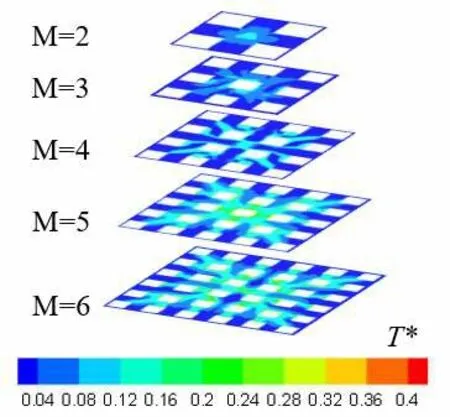
图5 不同街区行人层无量纲温度分布

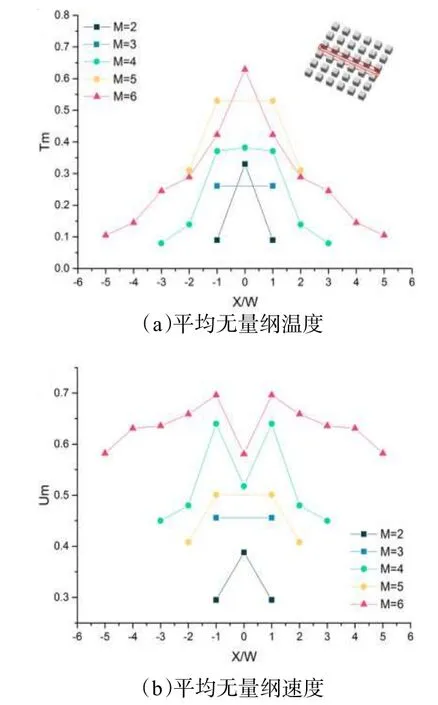
图6 不同街区峡谷内平均无量纲温度与速度

2.3 不同街道纵横比下的温度及速度分析

为了模拟案例具有对比性，本部分模型保持街道宽度W=30 m 不变，通过改变建筑高度H（分别取0.5H、1.0H、1.5H、2.0H）来探究不同街道纵横比对街区峡谷内的平均无量纲温度及速度的影响。如图7a 所示，在温度分布上，随着街道纵横比的增加，平均无量纲温度也随之增加，街区边缘峡谷内温差变化很小，街区中心峡谷内温差变化较大，最大处约为0.7 ℃，相较于上一部分增加建筑群数量来讲，增大街道纵横比会让街区中心峡谷内的温升趋势变化更加明显。在速度分布上，平均无量纲速度整体上随着街道纵横比的增大而增加。（图7b）。

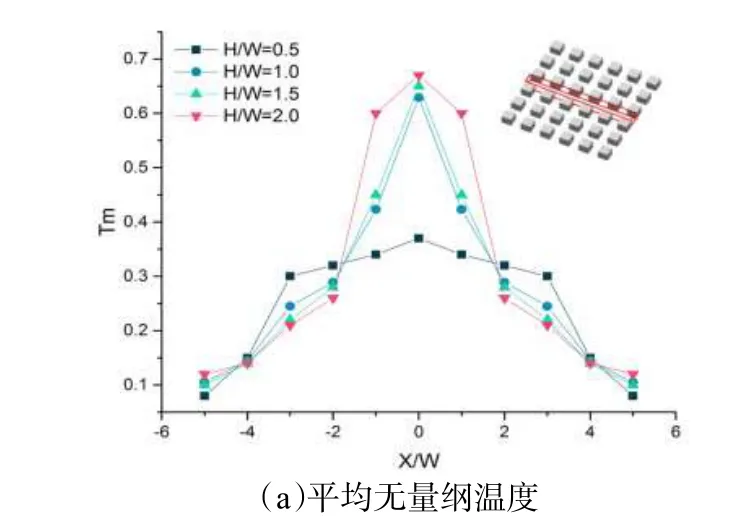
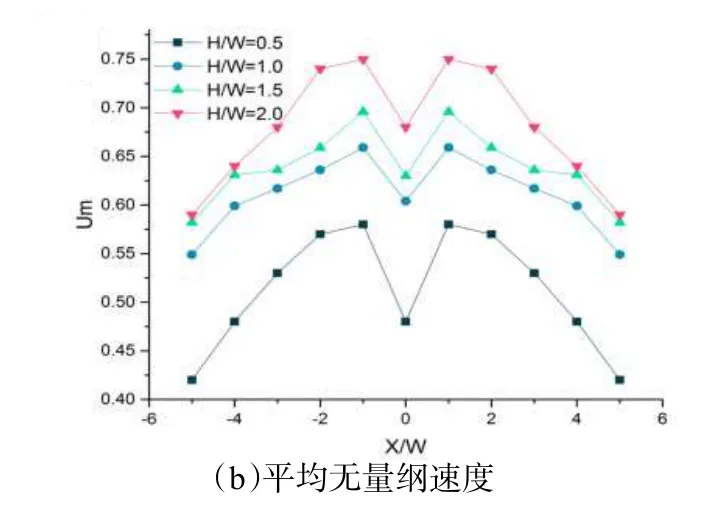
图7 不同街道纵横比街区峡谷内平均无量纲温度与速度

3 街区峡谷通风质量评价

3.1 三维街区峡谷换气率定义

本文评估的街区通风质量的指标是街区通风面上的空气交换率（ACH）[10]，空气交换率的概念表示在街区峡谷的通风面上每单位时间的体积空气交换，通过分析不同通风面的空气交换率以评估街区峡谷内的空气品质。与二维街区通风只能依靠街区顶部开口不同，三维街区多出了侧边通风面，为了研究其中具体的规律，相应的通风面定义如下[11]（图8）：

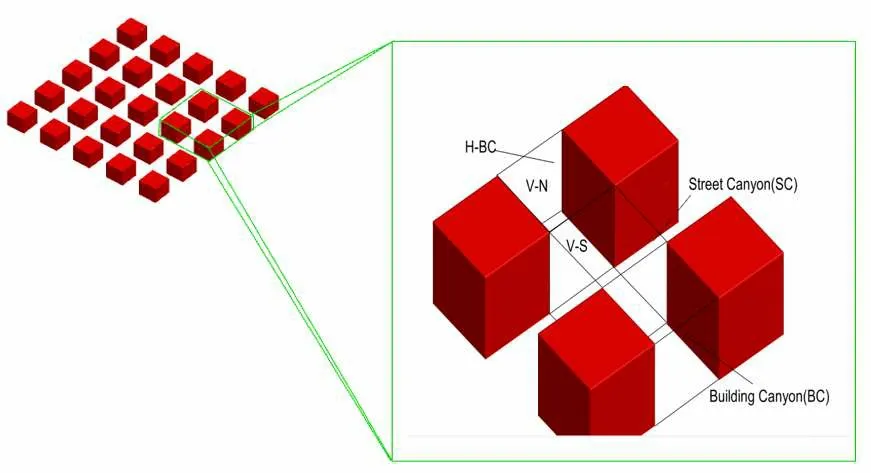
图8 计算域和一个子组

1）建筑之间的部分称为建筑峡谷Building Canyon（BC），中间十字街道的部分称为街道峡谷Street Canyon（SC）。

2）建筑峡谷部分侧边通风面分别为V-N 和V-S，顶部通风面为H-BC。

关于建筑峡谷的换气率可以考虑为顶部通风面空气交换率加上侧边通风面空气交换率之和，表达式如下所示：

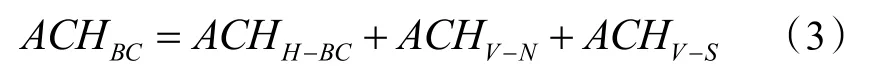
通风面上的空气交换率可分为两部分，分别是平均风引起的换气率为与湍流脉动速度引起的换气率ACH'，其中顶部通风面的由平均风导致的换气率计算式如下：

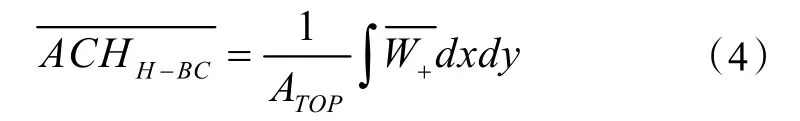
由湍流脉动导致的换气率计算式如下：

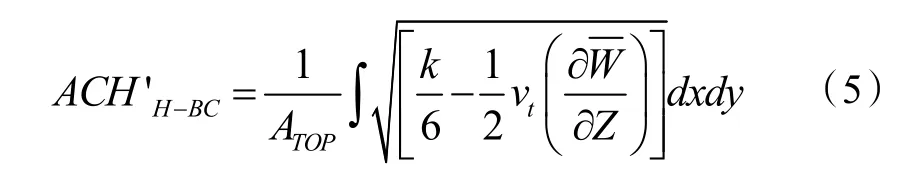
式中：k是湍流动能，vt是湍流运动粘度。

顶部通风面的换气率则为：

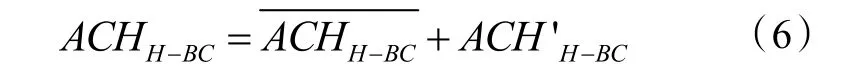
三维街区峡谷侧边通风换气率与顶部通风面换气率计算过程类似。

3.2 三维街区峡谷内换气率讨论

本部分主要从两个方面进行展开，一方面讨论了单个街区中顶部面和侧面空气交换率的规律，另一方面讨论了不同街区大小及不同街道纵横比下街区峡谷内的通风状况。为了便于比较，引进一个参考流量通量Qref=Uref×A，其中Uref取建筑高度的最大速度，A是通风面的面积，通过归一化处理，则可以得到一个新的ACH*=ACH/Qref。

如图9 所示，由于整个街区是对称的，所以选择图中标注区域部分进行研究，主要探讨街区中心到边缘部分换气率的影响。从图10 可以看出，街区峡谷顶部通风面上由于湍流脉动引起的换气率相较于平均流引起的换气率普遍较小，而且在街区中心部分差距愈加明显，主要是因为热压作用下，中心热量较大，造成了由街区周围向中心的收敛流，最后从街区中心峡谷顶部通风面流向上空。从街区边缘朝中心的方向上，无论是湍流脉动或者是平均流引起的换气率都有增大的趋势且街区中心位置上平均流引起的换气率变化较为明显。图11 主要是研究侧边通风面换气率的变化规律，主要可以将街区峡谷分为两个部分，分别是建筑峡谷（BC）和街道峡谷（SC），可以看出不管是湍流脉动或是平均流引起的换气率，街道峡谷（SC）的总是要比建筑峡谷（BC）的要高，主要原因是街道峡谷相较于建筑峡谷多出了两个通风面。另外由平均流引起的换气率在街区边缘峡谷内较高，而在街区中心区域较低，而由湍流脉动引起的换气率则展现相反的趋势。

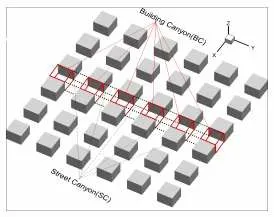
图9 街区峡谷示意图

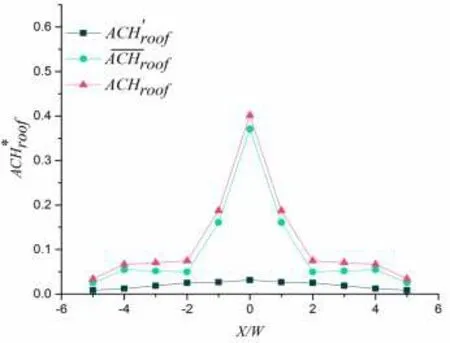
图10 街区峡谷顶部换气率随街区峡谷位置的变化规律

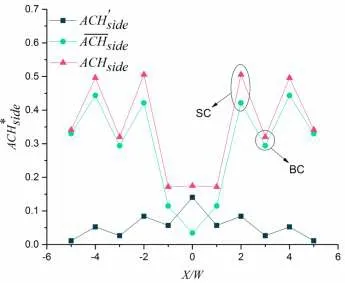
图11 街区峡谷侧边换气率随街区峡谷位置的变化规律

整体来看，不管是街区峡谷顶部通风面还是侧边通风面，由湍流脉动引起的换气率总是低于平均流，并且在街区边缘峡谷内，侧边通风面的换气率占主导，而在街区中心峡谷内则是顶部通风面换气率占主导。在街区边缘峡谷朝中心峡谷的方向山，总体的换气率不断降低，即中心街区峡谷内空气质量比较差。

对于不同街区大小和不同街道纵横比情况下的换气率研究，本部分取街区中心位置换气率进行计算。图12a 展示了不同建筑群情况下的换气率，随着街区不断增大，换气率也随之增加，在街区内建筑达到M=4 后，换气率变化逐渐趋于平缓。图12b 展示了不同街道纵横比下街区峡谷换气率变化，随着街道纵横比的增大，换气率随之变大，但是其变化率随着街道纵横比增大逐渐趋于平缓。可以看出不管是增加建筑群数量还是增加街道纵横比，都可以改善街区峡谷内空气质量的效果，但是其改善效果随着建筑群数量或街道纵横比的增加变得越来越差。

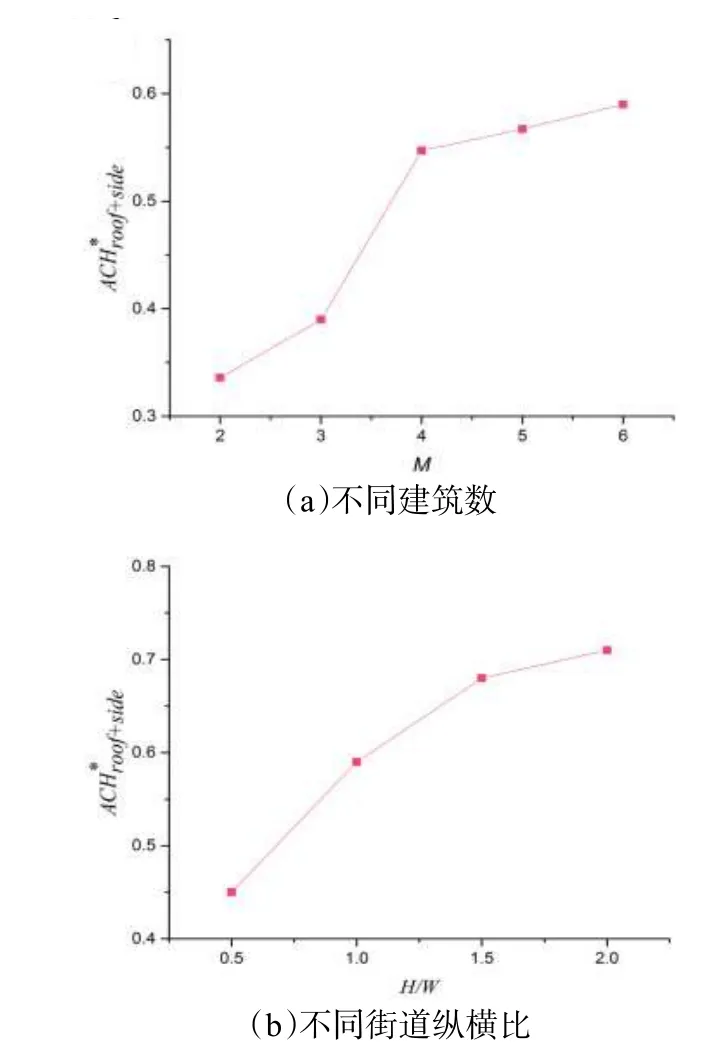
图12 街区中心位置峡谷内换气率的变化规律

4 结论

1）不管是单个建筑群还是不同建筑群，其中心位置峡谷内的温升较为明显，边缘温升无明显变化，说明由于压差驱动的收敛流对建筑群边缘降温较为明显，但是在街区中心峡谷部分却是对热扩散起到了抑制的作用。并且随着建筑群的不断增大或是街道纵横比的增加，其中心街区峡谷温升也是越来越高，最大可达到0.7 ℃。对于建筑群内的速度分布，主要是从边缘部分到中心的部分不断增大，但是在中心峡谷内却又开始减小。随着建筑群的不断增多或街道纵横比的增加，其整体平均无量纲速度也是在不断变大。

2）本文评价街区峡谷内通风质量的参数是换气率。首先分析单个建筑群的情况，整体上街区峡谷内的通风情况依靠的是平均流驱动的通风，并且街区中心峡谷换气率主要是由顶部通风面占主导，而街区边缘部分峡谷换气率主要是由侧边通风面占主导，而且在街区边缘朝中心的方向上，总的换气率是不断降低的，这也说明了街区中心位置空气质量较差。其次是在不同建筑群或不同街道纵横比的情况下，随着建筑群的不断增多或是街道纵横比逐渐增大，可以改善街区峡谷通风质量，但是其改善效果却是越来越差。