精细化壁面重构下的酸蚀裂缝导流能力研究

张雄，李春月，周舟，刘雨晴，周博成，考佳玮

1 中国石化西北油田分公司工程技术研究院，乌鲁木齐 830011

2 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

0 引言

酸蚀后的裂缝壁面形态参数是酸蚀裂缝导流能力重要影响因素，它有助于预测酸蚀裂缝导流能力和评价酸蚀效果。因此，酸蚀裂缝导流能力变化被广泛地研究。酸蚀裂缝壁面形态参数的精确化确定对于导流能力的预测尤为重要。

1973 年，Nierode等[1]在实验测量白云岩裂缝导流能力基础上，建立了N-K公式，主要考虑了岩石强度与溶蚀量与导流能力之间的等效关系，并建立了与闭合应力之间的联系；1978 年，Gangi[2]推导出了裂缝闭合距离与施加应力之间的“钉床模型”公式，假设裂缝开度分布为幂律分布；1999 年，GongMing等[3]假设微凸体受力后体积不变同时侧向变形，建立了酸蚀裂缝闭合模型；2016 年，Kamali等[4]假设酸蚀裂缝开度为不同高度的圆柱在应力高于单轴抗压强度时圆柱立即进入塑性，然后计算缝宽以及导流能力。

本文在前人研究基础上主要考虑了不同酸蚀裂缝壁面岩石力学形态参数以及力学性质的非均一性，将导流模型中所需要的壁面形态高度参数通过插值重构的方法精细化处理后应用到了酸蚀裂缝导流能力模型中，分析论证了利用不规则网格插值方法在裂缝导流能力研究中应用的可行性和适应性。

1 酸蚀裂缝壁面精细化导流能力模型

1.1 酸蚀裂缝导流模型

假设微凸体在所受应力小于其抗压强度时处于弹性阶段，σc=Eε，并且壁面支撑体假设符合累计概率密度为Φ(w)的某一分布N(w)，此时微凸体支撑裂缝，其所受应力与缝宽间的表达式为：

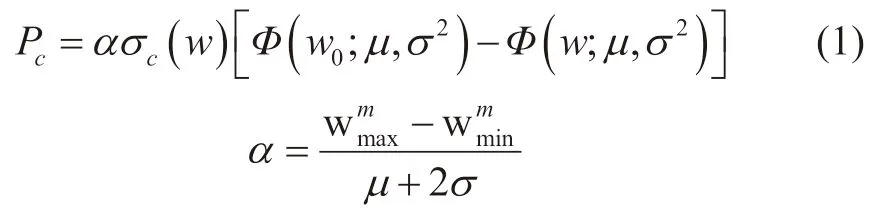
式中Φ(w; ，μ σ2)为服从均值为μ，方差为σ2的正态分布的累计概率密度函数。

α——裂缝真实接触面积修正系数；

μ——支撑体高度分布均值；

σ——支撑体高度分布标准差；

w0——裂缝壁面支撑体最大高度。

缝宽可用闭合应力的反函数表示：

此式可计算得到单一裂缝壁面的裂缝宽度，而整个酸蚀裂缝宽度可以用两壁面各缝宽之和表示，最后得到整体缝宽计算公式如下：得到酸蚀裂缝缝宽模型后，为更有利于现场应用，使用现场岩样测得的渗透率，代入导流能力计算公式可得相应变应力的酸蚀裂缝导流能力模型：

其中：k0——初始渗透率；

w——裂缝宽度。

通过数值求解模型，已知裂缝宽度后即可获得相应导流能力。其中的关键参数为裂缝宽度数据，这类数据主要包括支撑体高度分布的均值μ、支撑体高度分布标准差σ以及裂缝壁面支撑体最大的高度w0。在本文中将酸蚀后获得的壁面微凸体高度分布数据通过酸蚀裂缝壁面精细化模型重构后插值得到，以提高模型参数的精确化程度，从而应用到导流模型中实现准确化模拟。

1.2 裂缝壁面精细化模型

目前酸蚀裂缝壁面形态参数获取方法主要有机械式探针法[5]、光反射成像法[6]和激光扫描法[7-9]，现在主流的方法是激光扫描方法，即使用激光扫描仪以一定的扫描步长测量酸蚀裂缝的壁面高度，并且激光扫描仪的扫描步长对后期的酸蚀凸起的分析的刻蚀形态的展示影响很大[14]。为了减小扫描步长的影响，白翔等[15]采用傅里叶级数拟合离散的扫描数据点，通过计算平均残差计算得到了最优扫描步长。但是此类方法下由于人为或机器原因常使数据获取出现一定误差，如数据获取缺失、扫描精度低等问题，对于后续导流能力分析影响较大。因此本文从获得支撑体高度后的数据处理入手，利用不规则网格划分的方法进行壁面精细化重构，以获取更为准确的酸蚀壁面高度参数，更大限度减小误差范围。

酸蚀裂缝壁面采用不规则网格重构后是连续的曲面，酸蚀壁面任意位置的高度可以用这个位置在三角形面内对应的高度表示。同时，网格重构后的酸蚀壁面上某一位置的高度是由相邻空间3 点的高度进行计算得到，是一种空间插值方法。而常规方法如需得到任意一个位置的高度，则会使用位于同一直线上的相邻两点进行线性插值或者拟合计算。空间插值重建的壁面要比线性插值重建的壁面要更加精确，从而使用不规则三角形网格重构后的酸蚀裂缝壁面能够更准确地还原其真实情况。

不规则网格通过一系列互不交叉、互不重叠的连接在一起的三角形来逼近地形表面，每个三角形由最邻近的3 个点连接形成，此类建模方法在几十年的发展过程中已经形成了一系列较为成熟的三角形剖分准则，比如对角线准则和空外接圆准则等。

在所有的三角形网格中，Delaunay三角形网格在重构物体形状方面表现最出色。本文也使用这种网格重构酸蚀壁面。Delaunay三角形网是一系列相连但不重叠的三角形的集合，而且这些三角形的外接圆不包含这个面域的其它点。常规优化Delaunay三角网的算法是Lawson在1977 年提出的局部优化算法(Local Optimal Procedure， LOP)。LOP算法的主要步骤为：

(1)将两个具有公共边的三角形合并成一个四边形；

(2)用空圆特性检查三角形，若四边形的第四点(除检查三角形的3 点外)若在三角形的外接圆之内，就对四边形对角线进行对调处理。若不在，则不做处理。

对于不规则的数据，Delaunay三角网的剖分有许多剖分算法，但是主要使用的有以下3 种算法：

(1)1975 年 Shamos 和 Hoey[10]提出的分治算法。该方法时间复杂度小，但是在大量数据情况下内存消耗较大。

(2)1978 年 Green 和 Sibson[11]提出的三角网生长算法。该方法时间复杂度差，大部分时间都花费在搜索符合要求的第三点的过程中，效率低。

(3)1977 年 Lawson[12]提出的逐点插入方法。该方法实现简单、占用内存较小，但是它的时间复杂度差、效率低。

本文使用逐点插入方法对Delaunay三角网进行剖分，具体步骤如下：

(1)定义一个含有所有数据点的初始多边形(大三角形或者外凸壳；外凸壳指包含所有数据点且面积最小的凸多边形)；

(2)在外凸壳中建立初始Delaunay三角形网格；

(3)选择一个数据点加入到三角网中；

(4)寻找包含该数据点的三角形，将这个三角形与数据点连接形成三个新的三角形；

(5)使用LOP算法优化三角网，更新生成的全部三角形；

(6)重复第(3)、(4)、(5)步，直到处理完所有的数据点。

整个不规则三角形网格建模的流程见图1。

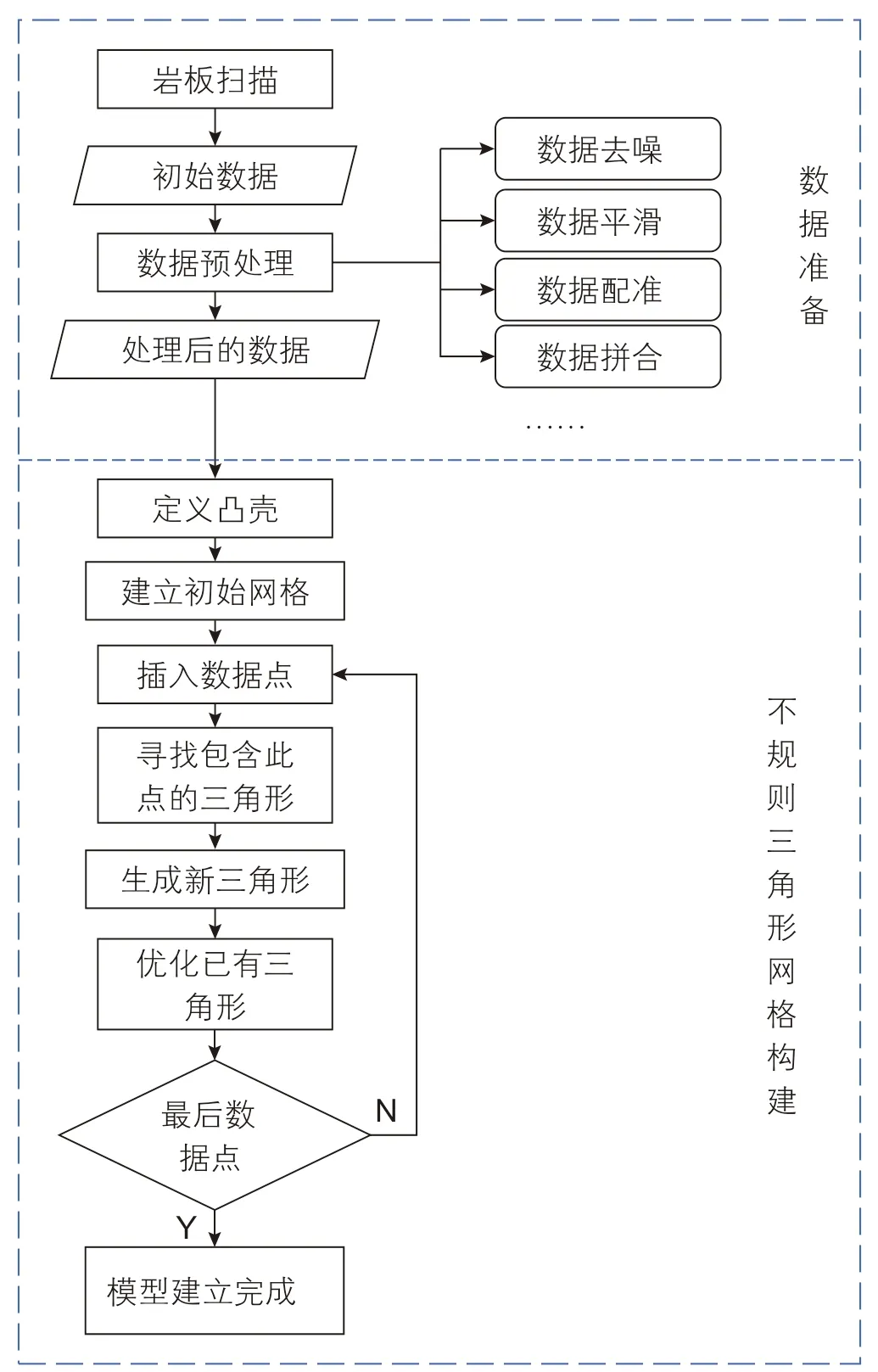
图1 建模流程图Fig. 1 Flow chart

不规则网格重构方法与其他重构方法相比的主要优点有：

(1)不规则三角网重构的精确性

原始高度数据受激光扫描间距影响，存在最小采样间距，本实验中为0.004 mm，而不规则三角网格重构后的裂缝壁面高度数据为连续数据，可以根据不同的需求进行采样绘图，最终网格采样间距为0.001 mm，本实验中不规则三角网格重构的裂缝壁面的精度以分辨率计算比原始高度数据提高 75%。

(2)不规则网格重构数据修补特性

在获取酸蚀裂缝壁面高度数据的过程中由于人为操作问题或者仪器的问题会导致某些位置的高度数据没有被获取到。同样，后期数据处理过程中会将某些位置的高度数据当做误差点删除，在一定程度上影响整体壁面高度数据。针对这种“空洞”利用不规则三角网模型重构就可以将其进行“填充”，这是因为不规则网格模型是以空间的三个点进行插值计算高度，能够使用“空洞”附近的高度数据对“空洞”的位置的高度进行插值计算，从而提高整体形态参数的准确性。

(3)不规则三角网重建裂缝流动通道

常规的原始高度数据重构裂缝流动通道操作非常复杂，但是在本次实验中使用不规则三角网模型重建后将上下壁面高度数据一一对应后可以很容易的重构裂缝流动通道(如图3)，有助于后续增产分析及判断裂缝支撑体接触情况。

图3 酸蚀后流动通道重建Fig. 3 Flow path after acid

2 酸蚀裂缝导流能力实验

2.1 岩板酸蚀实验

首先进行岩板酸蚀实验，实验在高温高压酸岩流动反应仪进行，该仪器能够模拟地层高温条件下的酸蚀情形。

图2 新重构方法与传统重构方法对比Fig. 2 Comparison of old and new methods

实验所用岩样取自塔河油田某区块露头，岩样主要成分为方解石和白云石，含有少量石英等其他矿物。共进行3 组酸蚀实验，各组有上下2 个实验岩板。酸蚀岩板尺寸符合API标准，尺寸为177.8 mm×38.1 mm×25.4 mm，见图4。

图4 酸蚀岩板Fig. 4 Samples before acid etching

将岩板在浓度为10% 纯盐酸，10 mL/min排量下分别酸蚀16 min、46 min、56 min，实验设计缝宽3 mm，获得酸蚀后的3 组导流板(如图5～7)。

图5 酸蚀16 min后的导流板Fig. 5 The guide plate after 16 min of acid etching

图6 酸蚀46 min后的导流板Fig. 6 The guide plate after 46 min of acid etching

图7 酸蚀56 min后的导流板Fig. 7 The guide plate after 56 min of acid etching

酸液刻蚀后使用高精度激光扫描仪测量酸蚀表面高度数据，激光扫描仪精度为0.005 mm，采样间距为0.004 mm，共获取高度数据约 320 万条。获取酸蚀壁面高度数据后，首先对扫描后得到的点云数据进行插值预处理，最终采样间距为0.001mm，然后进行不规则三角网格建模重构壁面，可以得到精确化的裂缝壁面重构形态参数，其形态图见图8～10，酸蚀后的微凸体高度分布比较符合正态分布，计算各个酸蚀裂缝壁面的正态分布参数见表1。

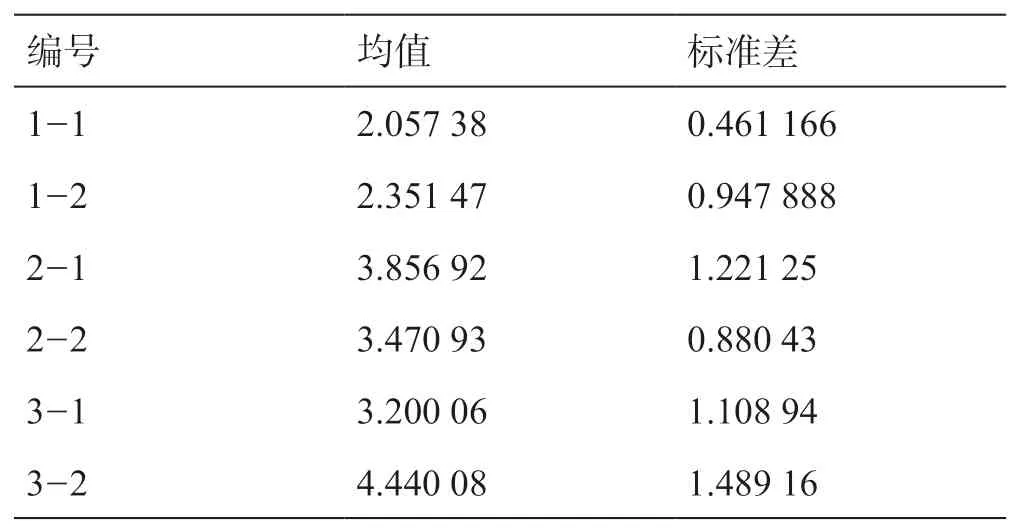
表1 正态分布拟合参数Table 1 Fitting of Normal Distribution

图8 16 min酸蚀后壁面形态Fig. 8 Morphology of wall surface after 16 min acid etching

图10 56 min酸蚀后壁面形态Fig. 10 Morphology of wall surface after 56 min acid etching

从表1 中可以看出，微凸体高度均值基本趋势为随着酸蚀时间的增加先增加后降低。部分高度均值较高如3-2 号岩板是由于其壁面主要分布大片不易酸蚀的白云岩导致。分析变化趋势原因可能为酸蚀壁面时间较短时壁面易溶物溶解较少，因此形成微凸体较少，高度分布较为均匀，岩样没有形成明显沟槽，呈均匀式腐蚀，而随着酸蚀时间的增加，易溶物溶解后难溶矿物变为微凸体支撑裂缝，壁面高度增加，当酸蚀过度时，如 56 min酸蚀后，作为支撑裂缝的难溶矿物微凸体破碎或被酸液溶蚀，整体壁面高度数值下降。

2.2 酸蚀裂缝导流能力实验

2.2.1实验目的

测定变应力条件下岩样酸蚀不同时间后裂缝的导流能力，获得变应力条件下的导流能力曲线。

2.2.2实验设备

实验使用支撑剂导流能力评价设备FCS-842，实验样品为3 组在浓度10% 纯盐酸，10 mL/min排量下分别酸蚀16 min、46 min、56 min后的导流板，规格为139.7 mm×38 mm×10～15 mm。

图11 FCS-842 导流仪Fig. 11 FCS-842 Hydraulic fracture conductivity test system

2.2.3实验方案

以蒸馏水为测量介质，在室温、一个大气压的条件下对这3 组岩板进行导流能力测试，选取6 个闭合应力点：3 MPa、10 MPa、20 MPa、30 MPa、40MPa、50 MPa，测量得到各应力点处裂缝的导流能力，实验结果见图12。

图12 不同酸蚀时间下导流能力曲线图Fig. 12 Curve of conductivity under different etching time

3 裂缝导流能力应用模拟及结果分析

将酸蚀16 min、46 min、56 min后的岩板插值得到的精确化壁面形态参数导入模型即可拟合得到不同酸蚀时间下的导流能力曲线如图13 所示。

图13 不同酸蚀时间下导流能力曲线对比图Fig. 13 Comparison of conductivity curve under different etching time

图中虚线为模拟结果，实线为实验结果，对比可知模拟结果与由实验结果基本吻合，可以较为准确的反映裂缝导流能力变化。

从图中可以发现，酸蚀16 min后在闭合应力较小时，初始导流能力值最大，如闭合应力为3 MPa时导流能力可达400 μm2·cm，而随着闭合应力增加，支撑体破碎，裂缝因支撑体破碎导致裂缝闭合，导流能力迅速下降，在围压达到30 MPa后导流能力基本下降为0。

酸蚀46 min后支撑体支撑性较好，闭合应力为3 MPa时导流能力相对其他2 个样品较低，为296.2 μm2·cm，但在闭合应力逐渐增加过程中，其导流能力下降缓慢，且可以维持在较高数值，在闭合压力增加至50 MPa后裂缝导流能力仍能保持在127 μm2·cm以上。

酸蚀56 min后处于过酸蚀状态，闭合应力较小时支撑能力强，模拟闭合应力为3 MPa时导流能力可达324.9 μm2·cm，但由于酸蚀过度，会导致裂缝整体抗压强度下降，支撑体更易破碎，最终在闭合应力增加至20 MPa时裂缝导流能力已下降至0。

综上分析，所建模型与实际结果拟合良好，在本次模拟条件下可以看出，酸蚀时间过短时未能形成有效支撑裂缝的微凸体结构，酸蚀过度后支撑体抗压强度下降导致裂缝无法维持高导流能力，因此应存在一个合理的酸蚀时间，即如图14，在较高闭合应力50 MPa下，酸蚀时间为45～50 min范围时，酸蚀裂缝导流能力较高。

图14 50 MPa闭合应力下导流能力曲线图Fig. 14 Curve of conductivity under 50 MPa

4 结论

(1)本文建立了基于缝宽条件下的裂缝导流能力模型，应用不规则网格插值得到的壁面形态数据，获得了不同酸蚀程度下的导流能力曲线图。

(2)利用三角形网格重建的酸蚀裂缝壁面能够更精确地得出酸蚀裂缝壁面的形态参数，同时三角形网格模型能够修补高度数据缺失的位置，重建裂缝流动通道，便于后续导流能力分析。

(3)通过模型得到的导流能力曲线图与实验所得数据拟合良好，将两个数据曲线结合分析，可以得到存在一个合理的酸蚀时间，使得裂缝导流能力在高闭合应力下能维持较高数值。