功能梯度材料输流管结构振动分析和临界流速

陈严飞 ，高莫狄胡东宗优刘宇冯玮

1 中国石油大学(北京)油气管道输送安全国家工程实验室/石油工程教育部重点实验室/城市油气输配技术北京市重点实验室，北京 102200

2 大连理工大学工业装备结构分析国家重点实验室，大连 116024

3 中集海洋工程有限公司， 深圳 518000

输流管道振动是引起管道机械磨损与疲劳失效的重要因素之一。当输流管道受到的激振力频率与管道系统的频率相等或者接近时，就形成了机械共振。此时，输流管道会发生较大的振动和变形，甚至破裂。在过去的几十年中，国内外学者对输流管道的动力学和稳定性开展了广泛的研究。据paièdousis和Issid[1]报道，Bourrières[2]首次对输送流体的管道动力学进行了认真的研究。Kuiper和Metrikine[3]分析了左固右简边界条件下管道的稳定性。悬臂管道在高流速下通过霍普夫分岔将发生颤振不稳定性[4-5]。Lee Sen Yung等人[6-7]考虑科里奥利力的影响，求解了倾斜旋转铁木辛柯梁的自由振动频率。郝逸、王文明等人[8]利用微元法分析了深水隔水管横向振动固有频率。厉曈曈、梁伟等人[9]运用积分变换求解了变截面深水钻井隔水管系统涡激振动问题。

功能梯度材料(简称FGM)是指材料属性随空间位置呈连续梯度变化的新型复合材料[7]。FGM可以通过设计体积分数的函数来任意调整功能梯度材料结构的特性[10]。在材料制备技术高速发展的今天，FGM在抗断裂[11]、耐磨损[12]等方面显示出远远优于传统材料的特性。然而，有关FGM的文献主要集中在FGM的梁、板和壳[13-16]，关于FGM管道输送流体的结构动力特性研究文献相对较少。

Sheng和Wang[17]研究了FGM管道在机械荷载和热荷载作用下的振动响应。Setoodeh和Afrahim[18]采用Galerkin方法计算了FGM管道的固有频率。边祖光等人[19]对正交各向异性功能梯度圆柱壳的自由振动开展了研究。Filiz和Aydogdu[20]研究了FGM纳米管中的波传播。Ansari等人[21]结合尺寸效应和哈密顿原理对输流管的固有频率进行了研究。Shen等人[22]、Dai等人[23]、You和Inaba[24]对非均匀材料输流管的稳定性进行了研究。刘辰[25]通过微分求积法研究了功能梯度输流管的振动及失稳。

虽然针对功能梯度材料输流管道结构振动问题国内外开展了一些研究工作，但目前大多采用近似方法得到，但整体计算精度较低，高阶收敛性较差。本文结合同伦分析方法[26]，给出了变材料输流管道的固有频率计算方法，并与其它近似方法进行了对比分析，证明同伦方法在具有较好的准确性同时具有非常好的计算效率，结合计算结果，进而给出了常见四种边界条件下临界流速与体积分数指数的图像，可以直观判断管道是否发生失稳，可以用于功能梯度材料输流管道结构分析和安全评价。

1 基本假设与基本方程

1.1 功能梯度材料输流管问题基本假设

假设管道材料为各向同性的黏弹性材料，流体不可压缩且无黏性，忽略管道运动对流体的影响，假设流体的流动速度方向垂直于管道横截面，速度大小平均分布，考虑管道材料为FGM，假设从圆心到管道截面任一点处距离为r，称为有效半径，内表面和外表面材料属性均可用密度、弹性模量和体积分数描述，则整条管道材料属性为

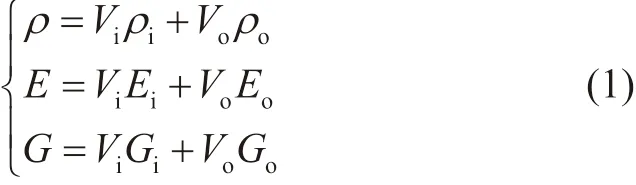
其中，ρ—管道材料密度，kg/m3;

E—弹性模量，Pa;

G—剪切弹性模量，Pa;

V—体积分数，%;

下标i，o分别代表内表面和外表面。

材料的体积分数V可以用式（2）描述

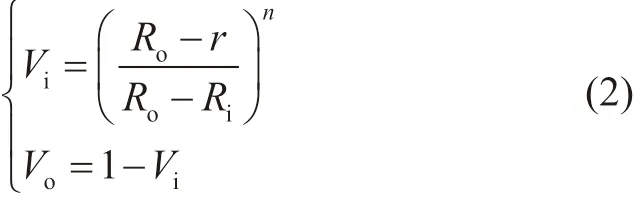
其中Ri和Ro分别代表管道内径和外径。

基于梁模型考虑以下4 种边界条件：

两端固支边界条件

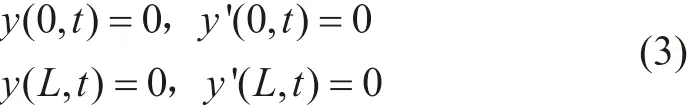
两端简支边界条件

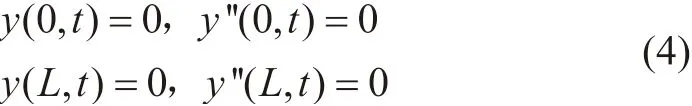
悬臂梁边界条件

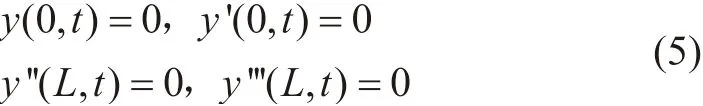
左端固支右端简支

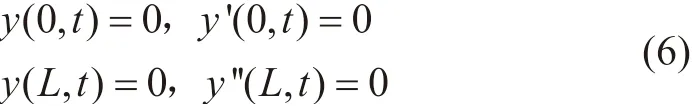
上述4 种边界条件中，y(x，t)代表着管道沿y轴方向的挠度，x和t分别代表空间坐标与时间坐标，L为管道长度。

1.2 功能梯度材料输流管问题基本方程

图1描述的是一条水平放置长为L的输送流体的管道，其横截面积为A，惯性矩为I，泊松比v为常数，流体运动速度为U。管道内径为Ri，外径为Ro，壁厚为h，则输流管的控制方程可以描述为

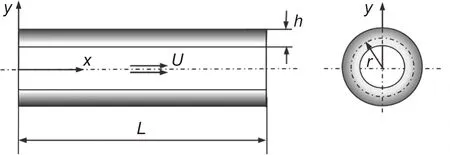
图1 功能梯度材料输流管系统示意图Fig. 1 Schematic of FGM pipe conveying fluid e system

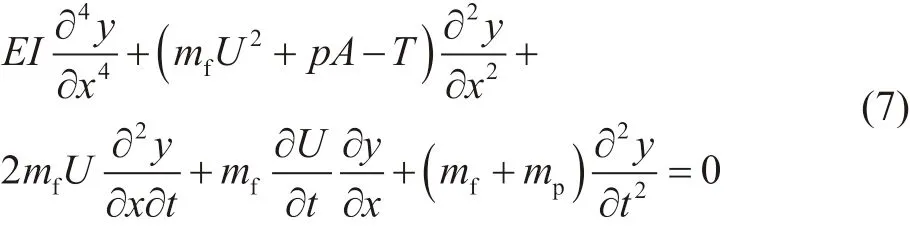
式中，E—材料弹性模量，Pa；

mp—单位长度管道质量，kg/m；

mf—单位长度流体质量，kg/m；

p—流体压强，Pa；

T——管道轴向拉力，N。

根据Euler-Bernoulli梁理论，不考虑内压以及轴向力，管输流体以恒定速度流动，则输流管系统控制方程可描述为

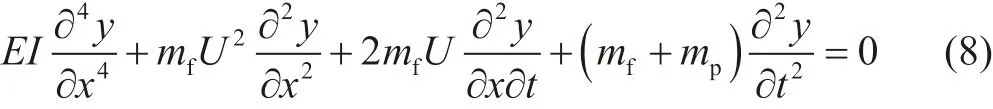
式(8)中，mp与mf分别代表单位长度管道质量与流体质量，y(x，t)代表着管道沿y轴方向的挠度，x和t分别代表空间坐标与时间坐标。

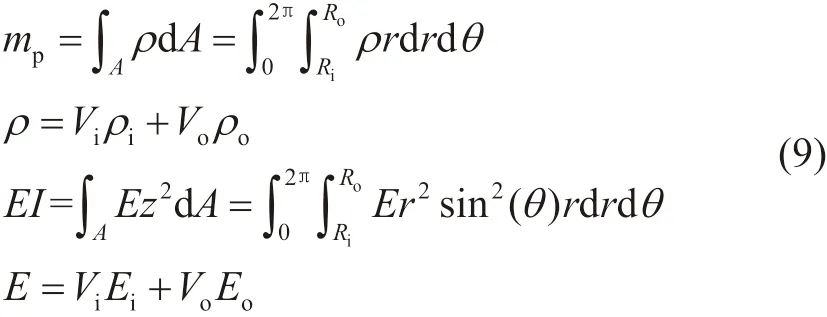
式(9)中，ρ—管道材料平均密度，kg/m3；

ρi—管道材料内表面密度，kg/m3；

ρo—管道材料外表面密度，kg/m3；

Vi—管道材料内表面体积分数，%；

Vo—管道材料外表面体积分数，%；

Ei—管道材料内表面弹性模量，Pa；

Eo—管道材料外表面弹性模量，Pa；

θ—有效半径参考点与竖直平面的夹角，rad。

对于式(8)，引入如下无量纲参数

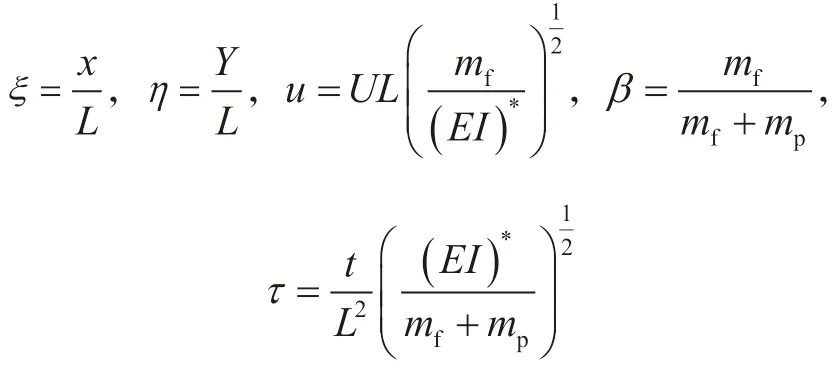
同时运用分离变量技巧，假设挠度方程为

则方程(8)转化为

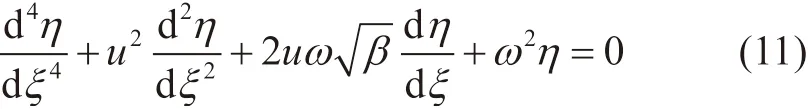
2 功能梯度材料输流管问题的同伦分析解法

2.1 同伦分析

对于式(11)，取线性算子

辅助函数取为

初始猜测解取为

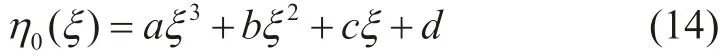
其中，a，b，c，d为4 个待定系数。

根据同伦分析法

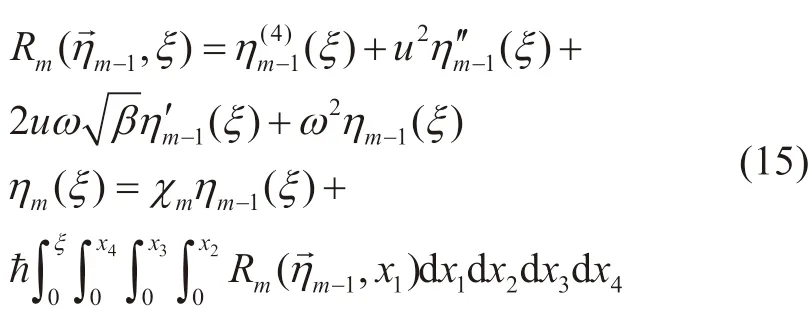
结合(14)和式(15)，可依次迭代得到n阶近似解

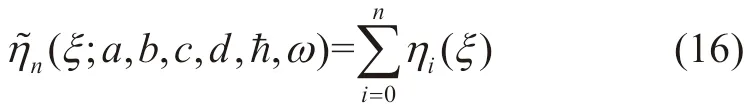
以两端固支为例，上式代入边界条件中，可得

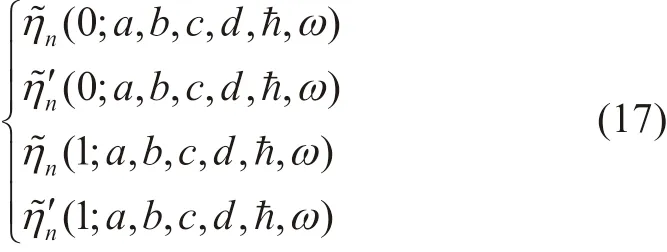
将式(17)整理为列向量矩阵乘法形式

其中，矩阵μ中的每个元素都是关于ℏ和ω的式子，矩阵λ= [a，b，c，d]T。

根据矩阵的性质，欲保证式(18)非零解存在，则必有

2.2 参数选择

式(19)描述的是ℏ（收敛控制参数，无量纲）和ω的隐函数关系式，对于输流管问题，ω一般为复数，这给ℏ—ω曲线的绘制造成了困扰。为了得到目标图像，本文将对[ -2，0]内的ℏ值离散为101 个点，对每一个离散点求解式(19)得到对应的ω值，这样就可以得到ℏ—Re(ω)和ℏ—In(ω)散点图。

选择表1 中的数据进行ℏ—ω的计算，考虑两端简支边界条件下不同体积分数指数及流速流体，分别计算得到ℏ—ω曲线图。每个ℏ—ω曲线图中都存在着ℏ的平整段。ℏ只有在这个范围内取值，计算结果才收敛。无论实部Re(ω)和虚部Im(ω)在取ℏ∈[-1.2， -0.8]的时候，同伦分析法可以计算得到收敛的近似解。同时图2 表明随着体积分数指数和流体流速的不断增加，ℏ平整段逐渐变窄，说明体积分数指数比和流体流速越大的时候，收敛控制参数的选取越受限制。

图2 基本输流管系统的ℏ-ω曲线Fig. 2 ℏ-ω curve of basic conveying fluid system

表1 FGM管道材料属性Table 1 Material property of FGM pipeline

2.3 收敛性分析

图3描述的是在两端简支边界条件下ℏ=-1，n=2，U=5 m/s输流管系统迭代20 次的前八阶频率，可以看出同伦分析法计算得出的一阶频率迭代3 次就已收敛，二阶频率迭代5 次收敛，三阶频率迭代7 次收敛，四阶频率迭代9 次收敛，更是在20 次迭代步数内八阶频率皆收敛。

3 结果分析

3.1 准确性验证

图2和图3 证明了同伦分析法解输流管系统问题的可行性，同时说明同伦分析法收敛性很好。在表2 中，同伦分析法(HAM)的计算结果与解析解[27]及DTM的计算结果保持一致，与DQM计算结果略有差异，这说明同伦分析法的计算结果是十分精确地，在计算精度上优于DQM。根据Ni[28]，DTM方法得到收敛的四阶频率值是在30 阶之后，而同伦分析法得到收敛的四阶频率仅需15 阶，这说明同伦分析法在计算速度上是优于DTM的。

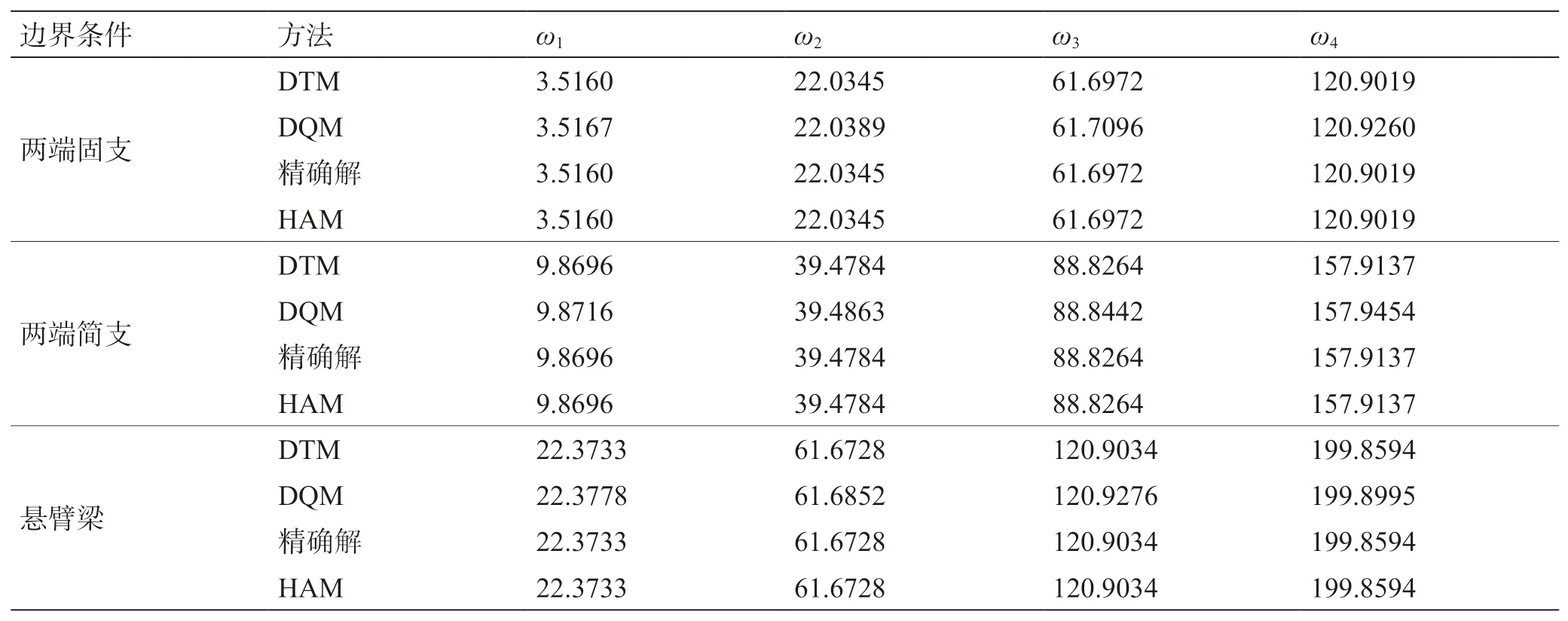
表2 在u=0 时同边界条件下的输流管自然频率Table 2 Natural frequencies of conveying fluid pipeline under different boundary conditions with u=0

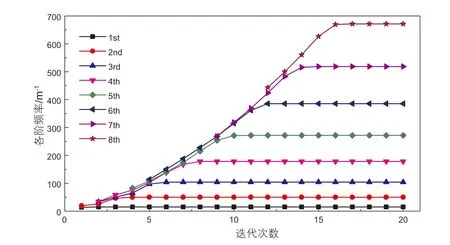
图3 两端简支边界条件下ℏ=-1，n=2，U=5 m/s 输流管系统迭代20 次各阶频率值Fig. 3 Natural frequencies of conveying fluid pipeline system with 20 iteration times under pinned-pinned boundary condition with ℏ=-1， n=2， U=5 m/s

通过同伦分析法计算无量纲流速u=0 以及u=2 的工况，并与EI-Sayed[26]的计算结果进行对比验证。在表3 中，流速增加时，输流管的自然频率会显著变化，而无量纲流速与管道长度有关，管道越长，无量纲流速越大，流体与管壁之间的相互作用也就越大。所以在对管道振动频率进行研究时，要考虑到流体与管壁之间的相互作用。

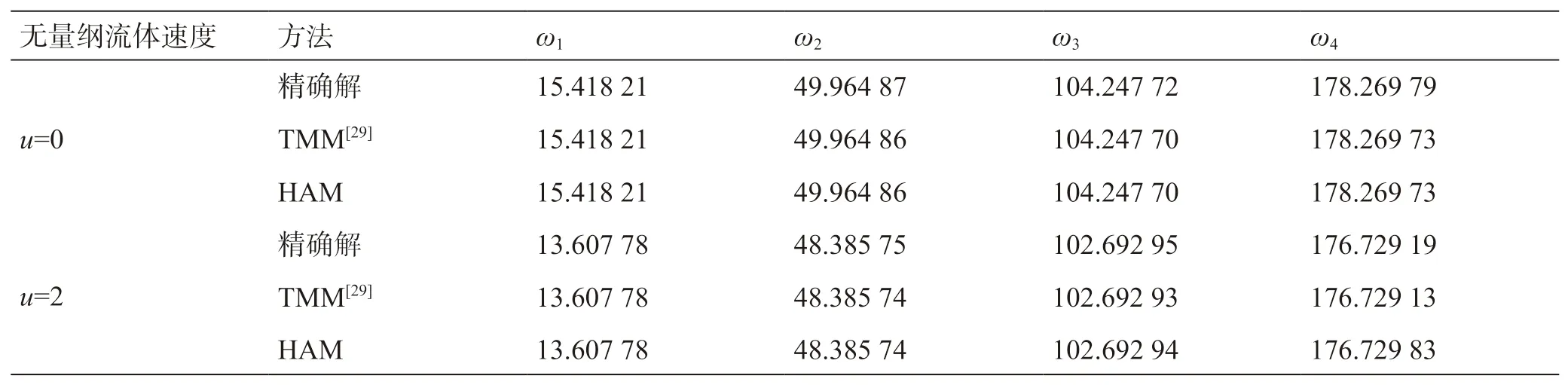
表3 β=0.5 时左固右简边界条件不同流速前四阶频率Table 3 First fourth order frequencies with different velocity under clamped-pinned boundary condition with β=0.5

3.2 临界流速

在输流管系统中，实部Re(ω)代表系统受到的阻尼，虚部Im(ω)代表系统的振动频率，当Re(ω)＜0，Im(ω)=0 时，系统称为静态失稳；当Re(ω)＜0，Im(ω)＞0 时，称为动态失稳；当时Re(ω)＞0，系统是稳定的；当时Re(ω)=0，系统处于平衡状态，这时对应的流体流速即为临界流速，所以我们通过衡量临界流速的大小即可判断系统是否失稳。

由于数值计算出的最终结果为虚数，其实部代表系统阻尼，虚部代表振动频率，所以很难直接绘制出振动频率与流体流动速度的图像，所以将U∈[0， 120]以1 为间隔离散为121 个点，对每一个流速进行计算，分别得到系统阻尼与振动频率，而后将计算出的结果按照Im(ω)＞0 从小到大进行排序，即可分别绘制U-Re(ω)与U-Im(ω)图像。

经过计算，得到了4 种边界条件下U-Re(ω)和U-Im(ω)的图像。由图可知，流速为零时，系统阻尼Re(ω)=0，随着流速增大，振动频率Im(ω)逐渐减小。图4 展示了两端固支条件下输流管系统阻尼与振动频率随流速的变化规律。对于两端固支、左固右简、两端简支边界条件而言，当一阶频率减小至零时，开始出现Re(ω)＞0，流速达到临界值，此时输流管系统平衡被破坏，整个系统处于静态失稳状态。当流速继续增加到一定值时，振动频率再次出现，这时的系统处于动态失稳状态。动态失稳状态下，随着流速的增加，U-Im(ω)图像将会出现叉型分岔，分岔出现后，一阶频率曲线与二阶频率曲线重合；对于悬臂梁边界条件，一阶频率减小至零时，系统阻尼仍然保持Re(ω)≤0，此时达到的速度不是临界流速，在经历了霍普夫分岔(分岔点处两阶频率并不重合)之后出现系统阻尼Re(ω)＞0，此时系统的流速为临界流速。

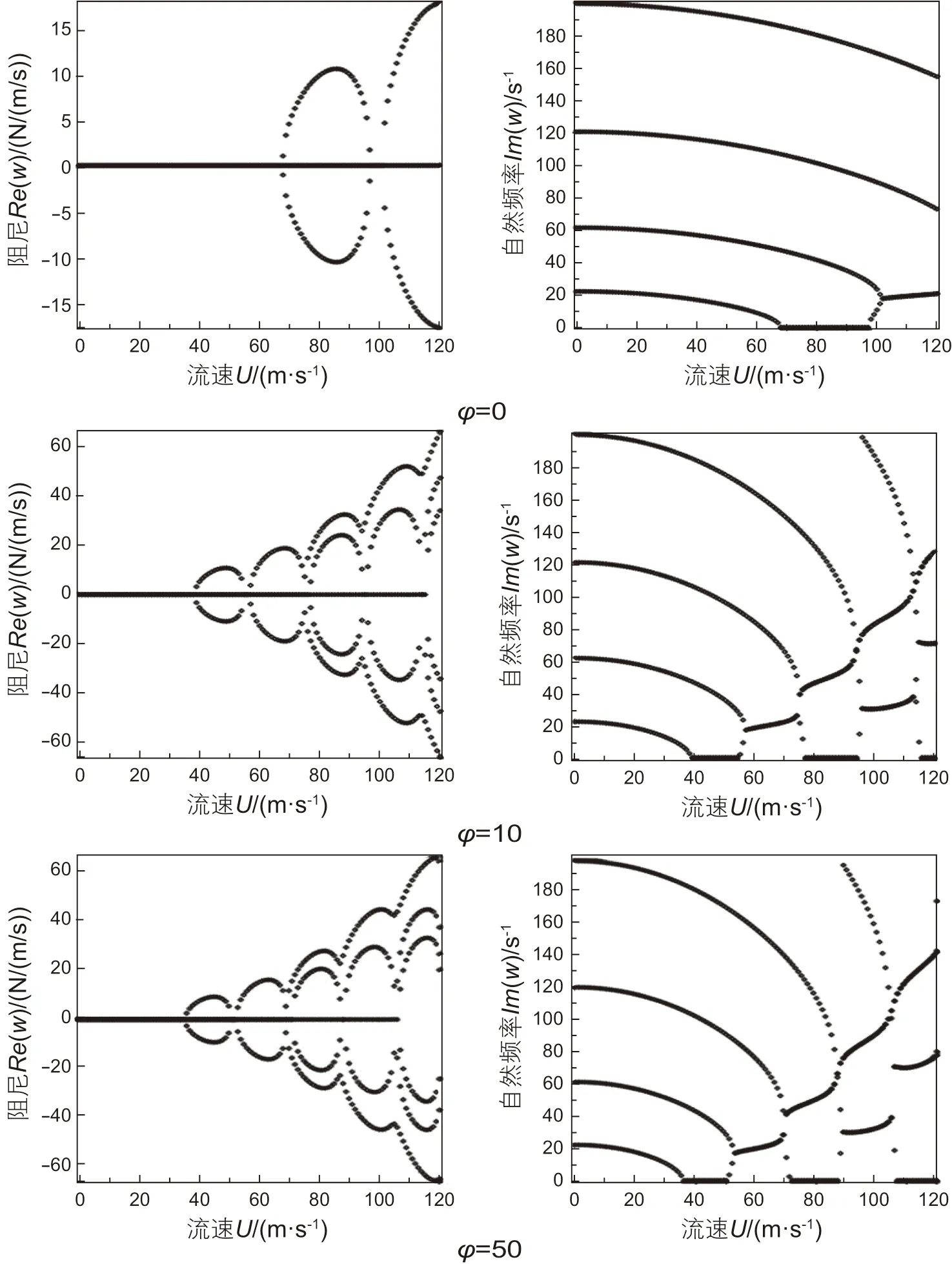
图4 两端固支边界条件下输流管系统自然频率与流体流速的图像Fig. 4 Diagram of natural frequencies and fluid velocity under clamped-clamped boundary condition

由图5 中可得，每一种边界条件下，不同的体积分数指数对应着不同的临界流速。同时随着体积分数指数φ的增加，临界流速不断减小，而且在φ≤10 的时候临界流速变化非常显著，在φ＞10 以后趋于平缓。因此在体积分数指数较小时，不能忽略其对管道自然频率的影响。在给定边界条件下任取一点，在曲线下方时表明输流管处于稳定状态，在曲线上表明输流管处于临界状态，在曲线上方时表明输流管处于失稳状态。所以在输送质量比不变，确定了管道材料的情况下，可以通过确认体积分数指数的值来确定输流管系统临界流速。

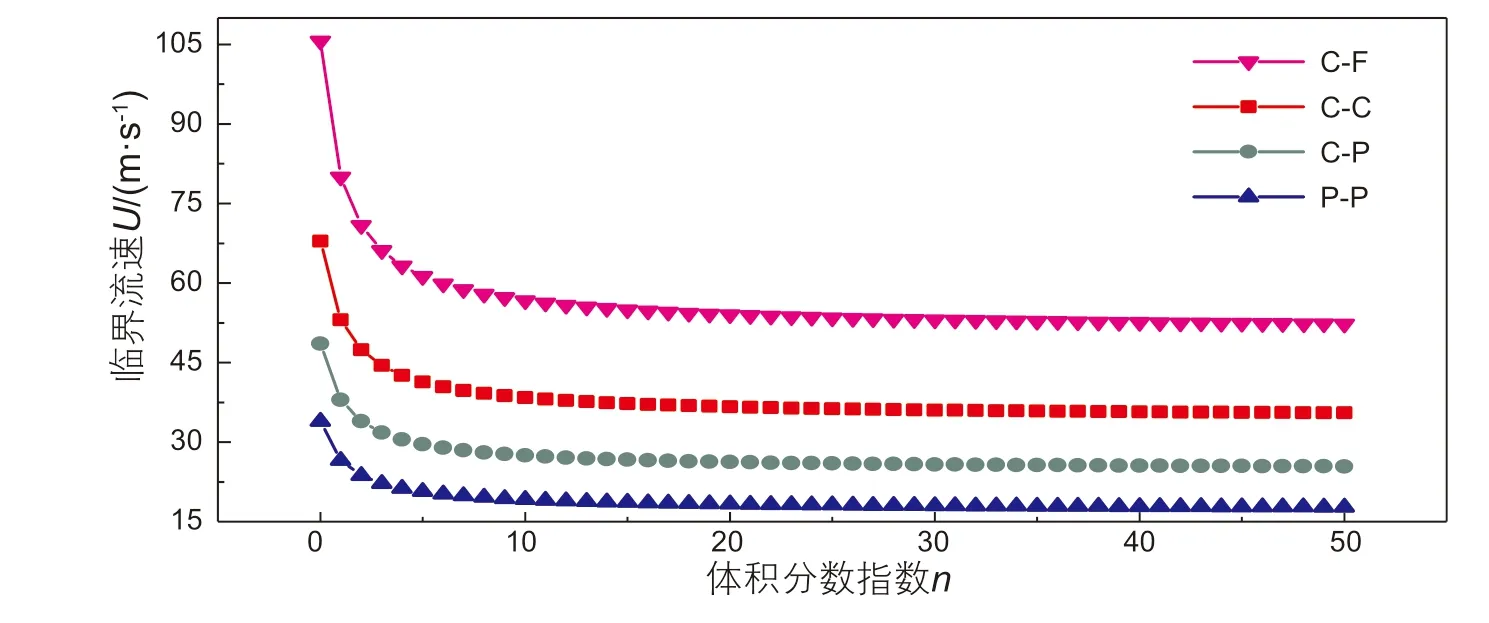
图5 临界流速—体积分数指数关系图Fig. 5 Diagram of critical flow velocity-volume fraction index

4 结论

本文基于同伦分析法提出了适用于不同边界条件下功能梯度材料输流管道自振频率的计算方法，得到的主要结论如下：

(1) HAM方法可以较为准确计算功能梯度材料输流管道的固有频率，计算高阶频率时收敛性好，收敛速度快，能提升计算效率。两端简支边界条件下，HAM方法得到一阶收敛频率仅需迭代3 次。同等条件下，DTM方法得到收敛的四阶频率值在30 步迭代之后，而同伦分析法仅需15 步迭代。

(2) 在体积分数指数较小时，体积分数指数对输流管固有频率的影响较大，随着体积分数指数的增加，输流管系统的固有频率迅速减小。因此，在体积分数较小时不能忽略其对自然频率的影响。

(3)给出4 种边界条件下的临界流速—体积分数指数关系图可以直观准确地判断变材料输流管道系统是否失稳，具有一定的工程指导意义。