经编织物气囊蒙皮梯形撕裂行为及破坏机制

2022-07-01陈建稳张若男王明洋马俊杰

哈尔滨工业大学学报 2022年6期

陈建稳，张若男，张阳，王明洋，马俊杰，范进

(1.南京理工大学理学院，南京 210094;2.中国人民解放军陆军工程大学工程兵工程学院，南京 210007)

平流层飞艇因在高空侦察、通信中继和空间探索等诸多领域具有应用优势，成为美国、欧盟、日本等世界主要军事大国研究的热点[1-3]。飞艇气囊发挥着封闭气压及承载张力的关键作用，是飞艇结构的重要部件[4]。而大跨充气膜结构由于其施工方便、节能环保、经济效益高等优点在现代社会获得大力发展，也因此成为中外学者研究的热点[5-10]。双轴向经编织物得益于独特的编织结构，抗拉强度及纱线物理特性利用率显著高于平纹织物[11-12]，并且在囊体用织物膜材的梯形撕裂破坏试验中，撕裂强力和抗撕裂延展性因纱线聚集也明显高于平纹织物。平纹织物结构中纱线存在卷曲结构，织物处于一种不平稳状态，在外力尚未完全施加于纱线之前，就有微量的伸长，也导致纱线的强力损失[11]，因此双轴向经编织物成为大中型飞艇气囊及尾翼、大跨充气膜结构主体材料的重要类型。然而气囊或气承膜面因其轻柔特征，往往会由于风致碎片、偶然刺破、焊缝拼接、初始缺陷等因素在膜面形成裂缝，使得膜材在过大的风、雪荷载或气压差下于裂缝周边产生应力集中而导致撕裂，进而撕裂扩展可导致膜结构发生整体破坏[13]。因此开展织物类蒙皮的撕裂性能研究对于现代飞艇气囊及充气膜结构的安全性设计与评估至关重要。

目前，膜材撕裂性能常用的测试方法有中心撕裂法[7-8]、舌形撕裂法与梯形撕裂法[14-15]。现阶段，膜材撕裂性能的研究方法大多集中在中心撕裂法，该方法与飞艇蒙皮实际撕裂破坏过程更为接近，但有待基于现有研究进行更新和完善，为飞艇蒙皮材料的撕裂破坏提供一个更广泛维度的参考。梯形撕裂方法的破坏模式单纯、结果稳定[16]，是现阶段国内外膜结构相关规范采用最多的方法，被欧美、日本等纳入膜结构设计标准[17-19]之中。现有的针对膜材梯形撕裂性能研究主要包括对涂层织物撕裂强度[20-24]、撕裂机理的研究[20,25-26]，以及与其他撕裂形式如单舌型撕裂的对比分析[20,26-27]。目前对经编织物类膜材的梯形撕裂研究相对不足，且多数梯形撕裂研究是基于在轴拉伸，即拉伸方向与纱线方向相同，缺乏对纱线偏轴状态下膜材的撕裂性能分析。鉴于膜材料的裂缝分布的随机性，有必要针对任意纱线偏轴下的梯形撕裂承载强度规律及裂缝延展破坏机制开展深入研究，从而为所涉及气囊蒙皮结构的安全性分析提供参考。

为此，本文针对典型双轴经编织物类气囊蒙皮，进行系列切缝长度、偏轴角度下的梯形撕裂试验与数值模型研究，阐释梯形撕裂拱形褶皱、应力翼型区形成与推进机制、以及偏轴撕裂破坏历程；深入探讨切缝长度、偏轴角度等因素对膜材梯形撕裂特征及破坏强度的影响规律，从细观层面阐释经编织物膜材梯形撕裂的裂缝破坏机制；基于分析所得强度规律，考虑剪切影响，提出撕裂强度预测理论公式。所得结论可为织物复合材料的裂纹止裂分析及膜结构安全性评估提供有益参考。

1 梯形撕裂试验

1.1 试验材料及试件尺寸

试验材料选取某典型双轴经编织物膜材，该膜材主要由基布、PVDF面层及各功能层复合而成。经、纬向纱线平直铺设无交织，二者辅以编织纱捆绑。其典型细观结构与经纱截面电镜扫描图如图1(a)、(b)所示。膜材厚度为0.73 mm，经、纬向纱线编织密度9×8根/cm。

试验采用如图1(c)所示的标准试件。试件是长、宽分别为150 mm和75 mm的长条型试样，在试样上标记等腰梯形，梯形两腰为夹持线，在等腰梯形上底边中央处与垂直方向设预切缝。当材料偏轴角度为0°时，设置4类切缝长度：5、15、25、35 mm；另设置6类偏轴角度：0°、15°、30°、60°、75°和90°。每组类型均做两个试件，以获得具有代表性的撕裂性能。

1.2 试验设备及加载制度

试验采用双柱落地式电子万能试验机UTM4000，试验机位移速率范围0.001～500.000 mm/min，变形测量范围10～800 mm，±1‰变形精度。沿梯形不平行两边夹住试样，使切口位于两夹具中间，长边处于褶皱状态。试验采用10 mm/min的加载速率进行拉伸，使试样沿着切口撕裂并逐渐扩展直至试样全部撕断。并用尼康D3400高像素照相机对该区域进行摄像，得到清晰的撕裂扩展特征及开口变化规律。试验室温度为(15±2)℃，相对湿度为(65±4.0)%。

2 撕裂破坏细观模型的建立

2.1 模型假设与参数设置

双轴经编织物类膜材由基布层与各功能层复合而成，其中经、纬向纱线协同编织，纱与基体之间的耦合作用十分复杂。为便于模型计算基本假设如下：1)纱线中纤维均质连续，编织纱的捆绑效果由基体替代；2)纱线和基体界面直接接触，黏结完全，无相对滑移；3)忽略复合材料中气泡与孔隙等随机缺陷，且不考虑复合材料中的残余应力、残余应变和环境影响；4)纱线为聚酯纤维材料，其本构参数由拉伸试验确定，经、纬向纱线的应力-应变关系如图2所示，其中经、纬向纱线卸载模量与各自初始弹性阶段模量相同，泊松比νv= 0.2[18]，其余主要参数见表1。基体主要由聚偏氟乙烯树脂构成，其弹模E0= 2 141.1 MPa，抗拉强度fs= 36.0 MPa，泊松比为νb=0.4[28]；5)断裂准则采用基于损伤力学演化的失效准则[18]，即经、纬向纱线抗拉强度作为最大主应力，取图2中经、纬向纱线最大应力值，即σult-w=508.15 MPa，σult-f=487.71 MPa，基体σult-b=36 MPa。选择Damage evolution建立材料的损伤演化准则。

图2 应力-应变曲线与本文采用材料模型Fig.2 Stress-strain curves and material model for this study

表1 纱线材料参数表Tab.1 Material parameters of yarn

2.2 数值模型建立与分析工况

数值模型基于撕裂试件有效区域建立，具体尺寸为25 mm×100 mm×75 mm(上底×下底×高)，厚度设置t=0.73 mm。经纱截面几何尺寸与经纱间距的具体参数设置如图1(b)所示，纬纱截面尺寸选用与经纱相同，但因经、纬纱线的编织密度差异，经计算纬纱间距为0.337 mm。按试验方案设置切缝长度及偏轴角度。细观结构建模依次建立内部编织纱线与外部包裹基体，经、纬纱线正交布局、无交叉缠绕。经、纬向纱线接触面采用Tie约束，以实现编织纱的绑定约束功能；纱线Embedded嵌入基体，二者力学效应耦合充分。整体数值模型单元数量为(1.09～1.67)×104。模型纱线与基体采用C3D8R六面体单元，该类单元可有效避免网格过度扭曲问题。

数值模型中的边界条件示意如图3(a)所示。定义SET-1、SET-2与SET-3分别为红框选中区域的纱线截面，RP1与RP2为参考点。膜材梯形撕裂测试时存在起拱效应，膜材面外拱起，使得材料处于面内外受荷状态。为有效模拟真实梯形撕裂效应，数值模型将引入此面外“拱鼓效应”。为此，模型共设置两个分析步，在STEP-1中设置RP1、RP2两参考点，分别与SET-3、SET-2耦合，转动两个倾斜边(BC-2和BC-3)，并使梯形长边的中间部位(BC-1)向Y方向运动，形成与试验对应的拱鼓结构，如图3(b)所示。在STEP-2中下边界(BC-4)采用ENCASTRE固定，上边界(BC-5)施加Y方向的位移(膜材所在平面为XOZ平面)。数值模型边界设置详细参数见表2。

图3 数值模型与试验边界条件Fig.3 Boundary conditions of numerical model andexperiment

表2 边界参数Tab.2 Parameters of boundaries

3 结果与分析

3.1 数值模型校核

本文将结合系列试验，对梯形撕裂数值模型进行细致校核，校核主要针对切缝长度与纱线偏转等因素开展。

1)典型切缝长度下数值模型与试验结果对比绘于图4、5，主要涉及梯形撕裂破坏特征(如图4所示)及承载曲线和变形位移(如图5所示)。据图4可知，在所选切缝长度下，数值模型可有效实现对非偏轴梯形撕裂破坏过程及裂缝扩展特征的细致模拟。在纱线断裂、膜面褶皱(图4椭圆A区)演变等方面，数值模型具有非常出色的破坏过程重现，对于应力集中区域(图4月牙B区)的分布与推进等机理破坏也可很出色地呈现(如图4(a)、(b)所示)。相应撕裂承载力曲线及变形结果(如图5所示)表明，数值模型可有效实现撕裂破坏承载力曲线各个特征段的科学模拟，撕裂承载力平均误差(相对试验值)小于7.4 %。

图4 典型切缝长度下数值与试验撕裂过程对比图(0°)Fig.4 Comparison of tearing process between numerical and experimental results under typical slit lengths

曲线波动段的锯齿状起伏特征与纱线的应力集中区的范围和纱线数量相关，数值模型在起伏幅度及数量方面具有良好的揭示能力。断裂位移预测结果与试验结果，误差小于6.3%，且随切缝长度增加，变形位移衰减特征一致(如图5(c)所示)。

图5 典型切缝长度下数值与试验结果对比Fig.5 Comparison between numerical and experimental results under typical slit lengths

2)典型纱线偏转角度下数值模型与试验结果对比绘于图6、7，主要涉及承载曲线(如图6所示)及梯形撕裂破坏特征(如图7所示)。由图7可见，纱线小角度偏转表现出沿纬纱方向撕裂扩展、膜面褶皱逐渐拉平的特征。数值模型可有效表现上述特征，并在破坏尾声处对纱线抽出破坏具有一定揭示(图7 C区)；在承载力方面,数值模型可清晰地观察到应力集中区域范围的变化趋势(图7 B区)，并且撕裂承载力平均误差(相对试验值)小于6.7%，反映出数值模型在模拟梯形撕裂的偏轴破坏方面良好的精确性。

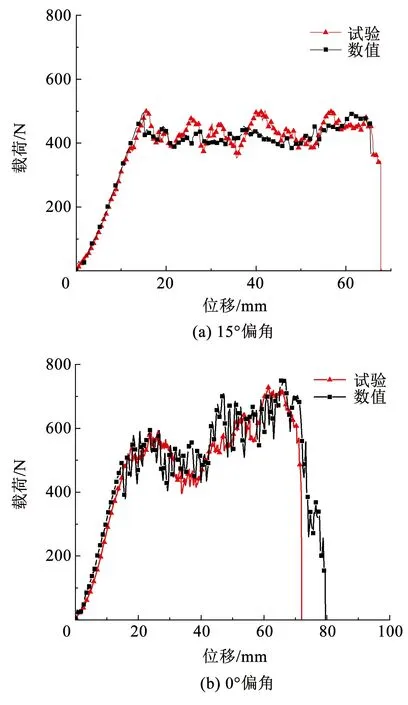
图6 典型偏轴角度下荷载-位移曲线试验与数值结果对比Fig.6 Comparison of load-displacement curves between numerical and experimental results under typical bias angles

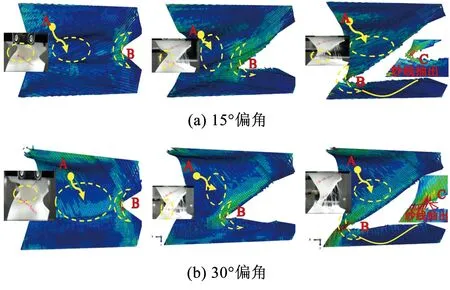
图7 典型偏轴角度下数值与试验撕裂过程对比图Fig.7 Comparison of tearing process between numerical and experimental results under typical bias angles

3.2 梯形撕裂破坏形态特征分析

经编织物膜材梯形撕裂破坏特征主要以基层的撕裂形态体现，在轴各切缝长度的梯形撕裂的破坏特征具有类似性，此处将针对偏轴0°切缝15 mm条件下进行阐述。在轴梯形撕裂依据破坏演变过程可基本分为如下几个典型历程：拱形褶皱与应力增长段、应力集中翼型区形成段、纱线断裂与翼型区推进段、撕裂尾段(如图8所示)。

1)拱形褶皱与应力增长。数值模型在各边界施加合理设置后，首先形成与试验类似的中间拱起的褶皱结构，如图8(a)所示。拱形褶皱区域松弛(图8 A区)，其余膜面处于张紧状态。随着位移增加，非拱形褶皱区域的纱线被逐渐拉长，在切缝前端周边区域的纱线应力逐渐增长，相应的应力云图如图8(a)所示。

2)应力集中翼型区形成。位移继续增加，切缝尖端处纱线应力增加明显，而相反方向的纱线应力降低梯度明显，形成典型的应力集中区域。该区域的纱线范围在同一工况下基本稳定，对于研究对象，承载主纱根数为5～7根。受纱线黏结摩擦因素以及圈纱绑定效果影响，应力集中区其余经、纬纱承担部分应力，其范围呈“翼型”分布，如图8(b)所示。翼型区以外主纱(A区)均处于扭曲状态，且由于纱线本身抗压刚度几乎为零，该部分纱线对整体撕裂抗力贡献极低。

3)纱线断裂与翼型区推进。纱线和各功能膜层被继续拉伸，纱线力学性能逐渐起控制作用，应力随变形增加较快。翼型应力集中区域的变化主要体现在横向的移动与竖向的扩展，当主纱应力达到极限强度时，将出现纱线断裂现象(如图8(c)所示)，此时抗力对应临界(首次)撕裂峰值；自翼型区的主纱发生破断后，翼型区将逐步推进，褶皱起拱区的长度开始减小；翼型区主纱陆续断裂失效，膜材总承载强度在保持高水平的同时起伏不定，在起伏变化的过程中，依次出现多个峰值(如图5所示)。此阶段主纱在变形过程中积蓄较高应变能，并急剧释放，之后新的主纱又快速积聚高应变能，如此反复便形成梯形撕裂锯齿状“屈服段”。

4)撕裂尾段。包括快速下降段和残余强度段，翼型区域的依次断裂，断裂过程不断重复，直至裂缝贯穿整个膜面。经历快速衰退期，扭曲状态下的主纱数量所剩无几，翼型集中区的主纱起主要承载作用，和图8(d)的最后一个应力集中区的出现基本相当，该阶段渐变区主纱的断裂失效，并最终失去整体承载能力。

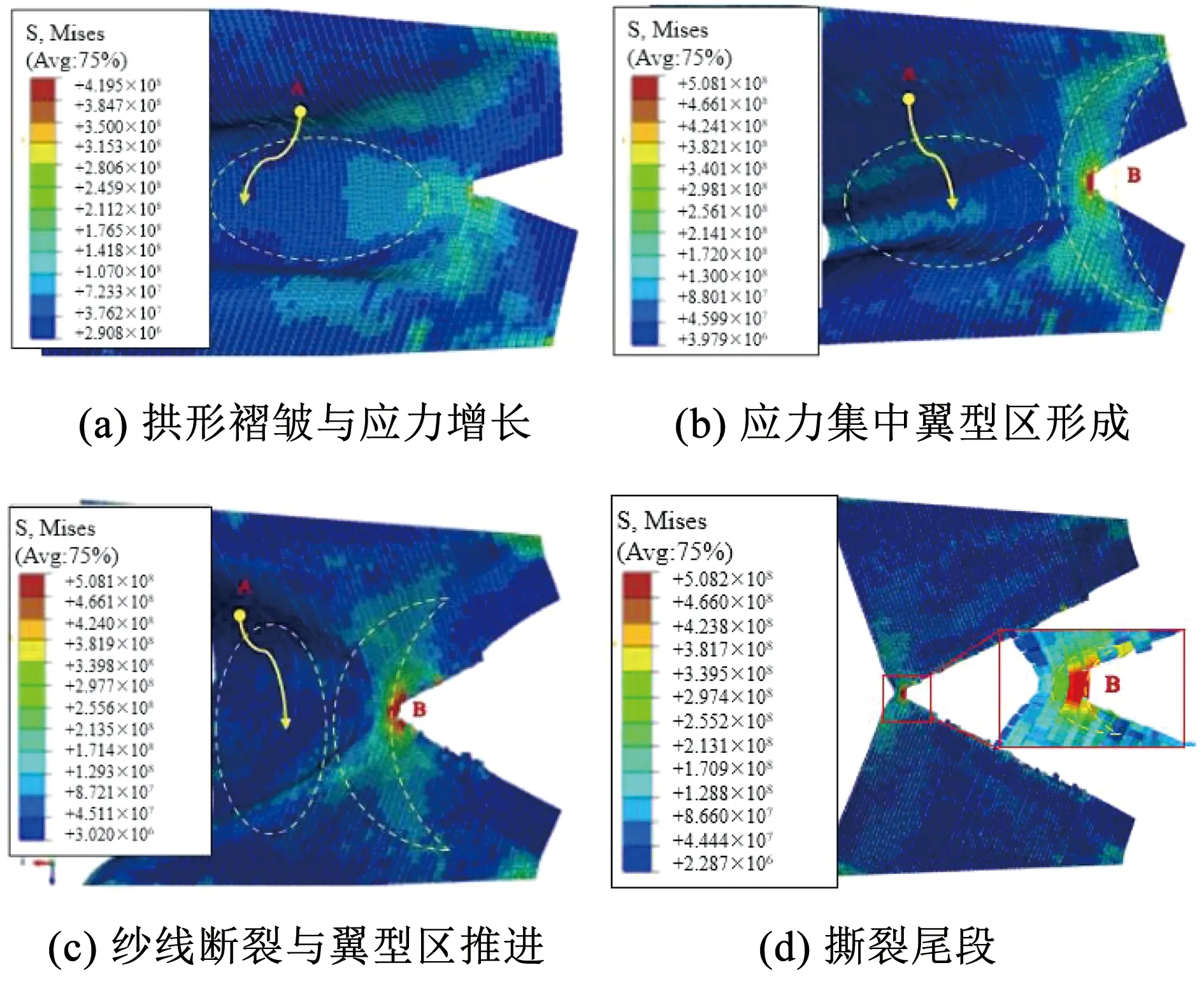
图8 蒙皮材料在轴梯形撕裂应力云图Fig.8 Stress nephogram of on-axis trapezoid tearing of envelope material

偏轴梯形撕的各特征阶段与在轴撕裂对应阶段的特征具有相似性，但也存在部分差异，主要体现在：应力集中区形状及偏转断裂延展方向，且纱线破坏以抽出失效为主(如图7所示)。

5)翼型应力集中区特征。纱线偏转可引起材料承载主向的变化。织物膜材内在细观结构复杂，相同边界及加载条件下纱线间的应力传递与分布因纱线偏转而发生规律性变化，应力集中区所表现的翼型特征随偏转角度的变化同样发生规律性转变。应力云图中翼型应力集中区表现出随偏轴角度增大，其范围存在从沿切缝周边条形分布向对称分布转变的趋势(如图9所示)。这种变化反映出不同偏轴角度下承载主向的改变，也预示着撕裂裂纹扩展的方向的变化。

图9 典型偏轴角度下应力集中区云图特征Fig.9 Nephogram characteristics of stress concentration zone under typical bias angles

6)裂纹扩展方向。在轴梯形撕裂裂纹扩展方向基本与荷载方向垂直，而偏轴梯形撕裂的裂纹扩展则表现出明显的偏轴效应(如图9所示)。裂纹将会沿着产生最大能量释放率的路径扩展，偏转角度的改变引起应力集中翼型区的变化，进而干扰裂纹扩展方向。当偏轴角度小于45°时，扩展方向与经纱方向垂直；当偏轴角度大于45°时，扩展方向与纬纱方向垂直。当偏轴角度为45°时，裂纹沿水平方向扩展，经、纬向纱线发生交叉杂糅破坏。此外，偏轴下纱线抽出破坏的特征较在轴更加明显(如图7所示)，纱线的抽出长度等特征均随角度存在一定规律性。

3.3 梯形撕裂强度受裂缝长度影响规律

撕裂强度是膜材重要的强度指标，其受切缝长度及偏轴角度的影响均较显著。参考文献[16]，梯形撕裂强度取自5个峰值抗力的均值，研究对象的切缝长度5～35 mm，梯度10 mm，相应强度变化规律，如图10所示。由图10可知，在轴与偏轴撕裂强度规律存在明显差异。其中在轴(0°，90°)撕裂强度随切缝长度增长呈线性趋势且略有上升；当切缝长度由5 mm增至35 mm时，膜材撕裂强度上升11.1%(0°)和13.7%(90°)。而对于偏轴撕裂，其撕裂强度随切缝增加而降低，在偏轴60°降幅最为显著，降幅达到34.4%。

图10 不同切缝长度与不同偏角时的数值撕裂强度Fig.10 Tearing strength for numerical models under different slit lengths and bias angles

梯形撕裂破坏属于局部性损伤，其破坏辐射区域及发挥承载的纱线组成及其变化是导致上述强度规律的关键原因。对于在轴类型，其撕裂抗力值与裂缝邻域内的应力集中翼型区域范围及纱线数目紧密相关，应力集中翼型区以外的纱线受褶皱卷曲影响基本不提供承载力(如图9所示)。为此，提取偏轴0°撕裂时，不同切缝长度下，切缝邻域内在临界撕裂时沿切缝方向纱线应力分布情况如图11(a)所示。可知，随切缝长度的增加，应力集中翼型区域范围非但未减小，而是略有扩展，翼型区主纱数量因此增加，并导致撕裂抗力值的适度增长。此外，应力集中翼型区增长幅度存在放缓趋势，可以预见随切缝长度增加，在轴撕裂强度随切缝长度增加存在一个限值。典型偏轴(30°)时相应切缝邻域的应力随距离变化曲线列于图11(b)，可见随着切缝长度的增加，沿撕裂扩展路径上的应力集中程度在逐渐下降，使得整体撕裂抗力也随之降低。

3.4 梯形偏轴撕裂强度规律与预测理论

偏轴角度对于撕裂强度的影响规律如图12所示。可知随着偏轴角度增加，膜材撕裂强度先增后减，整体呈倒“V”型变化规律。在0°偏轴情况下，切缝邻域内经向纱线可近似承受类剪应力；当偏轴角度适当增加时(如15°和30°)，鉴于前文研究可知，裂缝并非杂糅发展，而是将沿纬纱方向扩展，由此裂缝邻域材料处于拉剪耦合应力状态，裂缝尖端区域主纱受垂直于经纱方向的剪应力以及沿经纱方向拉应力的共同作用。由于纱线受拉能力较强, 而受剪能力较弱, 拉剪耦合状态下的抗撕裂能力远大于在纯剪切状态下的情况。基于上述分析，45°材料同样处于拉剪耦合作用下，且此时经、纬纱线位置对等，协同承载能力增强，撕裂强度明显被强化。因此，在从较小偏轴(15°和30°)过渡到大偏轴(60°和75°)的过程中，抗撕裂能力先增大后减小。基于强度结果(如图12所示)，纱线偏转角度0°～90°，撕裂强度呈典型倒“V”分布特征，45°区域局部峰值的出现，与材料内在组成纱线结构的细观受力直接相关。

图12 不同切缝长度与不同偏角下蒙皮材料梯形撕裂强度Fig.12 Trapezoid tearing strength of envelope material under different slit lengths and bias angles

图13显示了4组梯形偏轴撕裂过程中等效应力云图，各偏轴角度下承载主纱存在差异。偏轴角度为0°时由经纱主要承载(如图13(a)所示)，随着偏角逐渐由0°向45°转变，经纱逐渐降低承载比例，纬纱逐级提高其承载比例。当偏角为45°时应力集中翼型区经、纬纱均呈现高应力状态(如图13(d)所示)，此时承载主纱从经纱最终演变为经、纬纱平分荷载。为细致探讨承载机制，两类典型角度45°与15°下切缝尖端邻域经、纬纱线的具体应力分布曲线绘于图14。

图13 蒙皮材料撕裂过程中应力云图(W-经向，F-纬向)Fig.13 Stress nephogram of envelope material during tearing(W-warp，F-filling)

纱线的承载机制受偏轴影响显著，根据图14，各自相邻的经、纬纱线应力峰值出现表现出节奏鲜明的时差特征，峰值交替出现且依次发生断裂。在偏轴角度为45°时，经、纬纱均在达到极限强度后发生断裂，充分发挥了纱线的承载能力。而偏轴角度为15°时，由于纬纱与加载方向处于大偏轴角度，纬纱整体承担荷载水平较小，小于经纱承载水平的50%，且其应力主要是由经纱传递的剪切力造成的。可见，膜材撕裂强度与材料细观结构受力及变形紧密相关，并受应力集中翼型区范围与形状干扰。其中45°时，经、纬向纱线相互协调变形、协同承力，各自承载能力发挥充分，是材料在拉剪耦合应力下的细观最优承载机制的典型状态，45°局部峰值的出现是上述最优承载机制的一种体现。

图14 切缝邻域处纱线应力变化曲线Fig.14 Stress of yarns in slit vicinity

撕裂作为织物类膜材的关键破坏机制，国内外对其强度规律及理论进行不懈探索[16,29-32]。其中对于梯形撕裂强度，张营营等[16]考虑了材料抗拉强度、开口尺寸及夹持倾角等影响因素，提出了基于拟合结果的梯形撕裂强度预测公式。织物类膜材属于正交异性复合材料，具有典型的各向异性特征。加之裂口随机性存在，为深化梯形撕裂强度理论，提高工程适用性，考虑前文所述膜材梯形撕裂剪切应力效应显著，本文基于正交异性材料剪切参数理论[33](式1)，将剪切因素的影响充分纳入强度理论，提出了基于倒“V”型关系的梯形撕裂破坏纱线的偏轴强度理论(式2)。

(1)

式中：E为弹性模量,G为剪切模量,v为泊松比,θ为试样偏轴角度,w、f分别为纱线的经、纬向。

(2)

式中：σT为梯形撕裂强度；X、Y分别为15 mm切缝长度下经编织物膜材偏轴角度为0°、90°的撕裂强度;R为膜材剪切强度，通过偏轴拉伸试验确定[33]上述变量单位均为N；α为剪切影响系数，取值0.25。设置参数β用来表征切缝长度效应，当切缝长度由5 mm增至35 mm时，β的取值分别为22.3、21.5、19.2、18.3。α和β通过最小二乘法确定。泊松比ν取值0.4[28]。

所提理论公式可考虑剪切与泊松比参数，对梯形撕裂的破坏机制具有更多层次的挖掘和阐释，所提理论预测可有效跟踪撕裂强度倒“V”型变化趋势(如图15所示)。图15中5、15、25、35 mm均表示切缝长度。结果分析表明：对于不同切缝长度下的理论预测结果相对数值结果，平均误差小于14.0%，其中切缝长度较小时误差略有扩大，可能与膜面面外形态与应力状态的复杂效应有关。整体上，理论预测与数值结果具有良好的一致性，预测理论表现出良好的适用性。