垂直轴升阻型风力发电机启动特性的优化

2022-07-01张博文徐钦旭胡振宇李志捷黄忠文

武汉工程大学学报 2022年3期

张博文，徐钦旭，胡振宇，李志捷，陈玥，黄忠文*

1.武汉工程大学机电工程学院，湖北武汉 430205；

2.哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨 150001；

3.武汉工程大学管理学院，湖北武汉 430205

随着传统能源的枯竭，风能成为了研究热点之一，使得风力发电机的研究也备受关注。目前垂直轴风力发电机（vertical axis wind turbine，VAWT）研究的方向主要有增加风力发电机的相关外置结构［1］和优化叶片结构。不同种类的叶片中，S 型叶片风力发电机容易启动［2］，而D 型叶片风力发电机具有更高的风能利用率［3］，但其在较大流速的流场内才可启动。D 型扇叶种类较多，其中H 型应用较为广泛。H 型扇叶的叶尖速比（tip speed ratio，TSR）高，风能利用率在TSR 为2～3 之间［4］最佳，而S 型扇叶经过偏转12.5°后风能利用率有所提高，且最大值对应的TSR 在0.8～1.0 之间［5］，但H 型扇叶的整体风能利用率比S 型扇叶高。当S 型VAWT 的横向重叠比e/d为0.2 时，整体效率达到最高，S 型VAWT 以125°为启动角度时，其力矩系数达到整体最低，此时的启动效率相较其他角度时低［6］。针对该问题，将H 型优化为混合型扇叶，并与S 型扇叶结合设计，使降低启动风速及提高整体效率的效果更加明显。

1 叶片模型及参数设定

为了提高S 型VAWT 的整体性能并降低H 型VAWT 的启动风速，如图1 所示，将混合型H 型扇叶与S 型扇叶结合设计；S 型扇叶的半径d与H 型扇叶的弦长c比值设为1∶0.265［7］，针对θ=125°时，S 型VAWT 相对整体效率最低的问题，对H 型扇叶进行优化处理。H 型扇叶对以NACA0012 翼型作为原型的H 型扇叶进行优化处理。两个无量纲系数作为翼型性能参数。

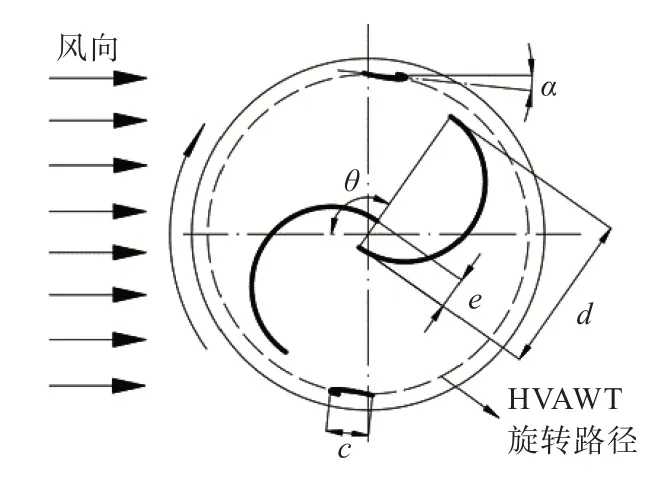
图1 截面示意图Fig.1 Schematic diagram of section

升力系数

阻力系数

其中面积A取翼型截面，u取风力发电机的迎风速度。

叶轮中流体的流动状态对翼型的性能参数有一定影响，流动状态由雷诺数表达

其中υ为黏度系数。

与此同时，翼型的俯仰角度不同，其性能参数CL/CD也不同，如图2 所示，Re≤400 000 时，俯仰角度α取5°升阻比最大；Re＞400 000 时俯仰角度α为6°最佳角度。Re越大，S 型VAWT 的相对风能损耗越大，需用H 型扇叶进行弥补，故当θ=125°时α取6°。

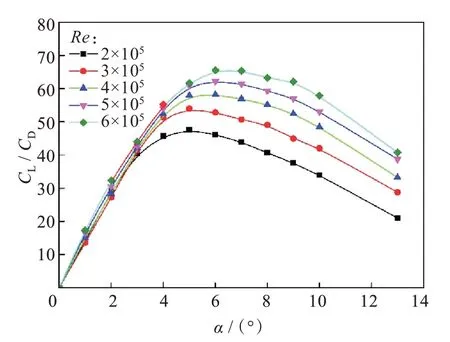
图2 升阻比系数Fig.2 Lift-drag ratio coefficients

当H 型叶片弦线与来流轨迹平行时，由于NACA0012 翼型的对称性，使得该角度下的H 型扇叶无升力产生，但有阻力，且此时S 型扇叶力矩系数贴近最低力矩系数，因此将H 型扇叶优化为升力与阻力混合型扇叶，如图3 所示，S 型扇叶外端点切线与H 型扇叶交于p1，当θ= 90°时，翼型尾端点c1至p1处为阻挡S 型扇叶接收来流的部分，作翼型弦线的垂直线与翼型构造线交于p1、p2点，裁剪翼型c1至p2外型部分，使得c1p1处接受来流产生阻力，并利用该阻力形成推力。c1p1可将流体导流至p1c2p2处聚集，产生更大的阻力推动扇叶转动，此时H 型叶片为阻力型扇叶。

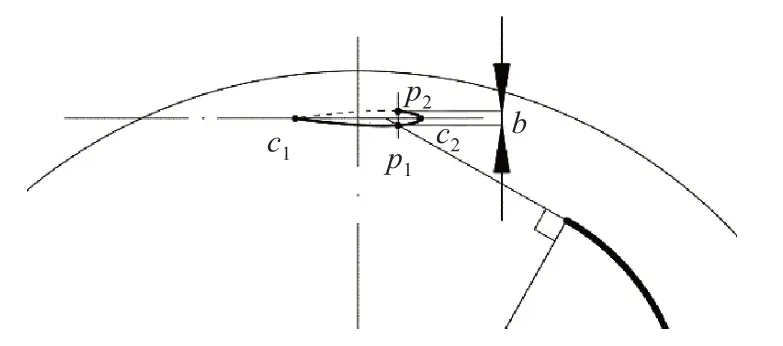
图3 H 型VAWT 结构示意图Fig.3 H-type VAWT diagram

叶轮继续转动，推动H 型扇叶转动的力由阻力逐渐转变为升力。转动过程中，H 型扇叶可为阻力型、混合型或升力型扇叶，而S 型扇叶主要作为阻力型扇叶降低叶轮转动的启动风速，并提高阻力作为推力的效率。

2 概念模型建立与分析

2.1 风力发电机性能参数

风力发电机旋转的过程中存在叶尖速比与旋转的速度相关，是风力发电机的性能参数之一，且风力发电机的角速度相较线速度便于测得。风力发电机的叶尖速比

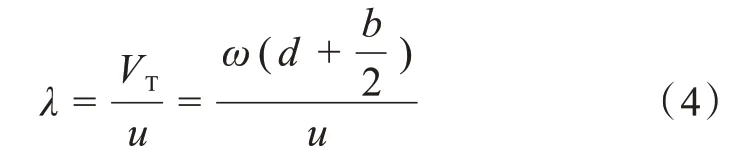
叶轮转动的同时，所接收的风能转换为电能。风力发电机视为一个系统，将该系统放置于一个无限大的空间中，该空间存在稳态流动的流场，根据热力学第一定律

式中ΔU为风力发电机做功时损失的能量，QW为叶轮接收的风能，PT为风力发电机做功的能量。叶轮接收的风能与叶轮的扫掠面积（H 型扇叶扫掠面积+S 型扇叶扫掠面积）及来流速度有关，风力发电机做功与其力矩和角速度相关，则风能利用率CP为：

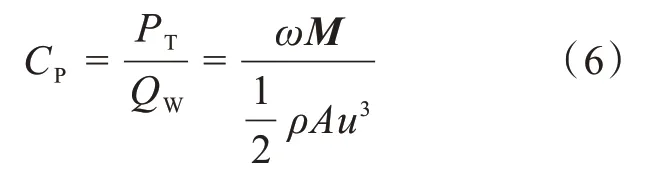
其中M为力矩，ρ为空气密度。叶轮的力矩系数为：

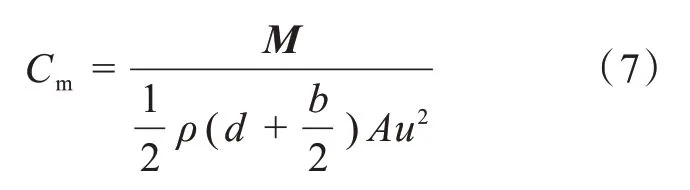
将式（4）和式（7）代入式（6）得到

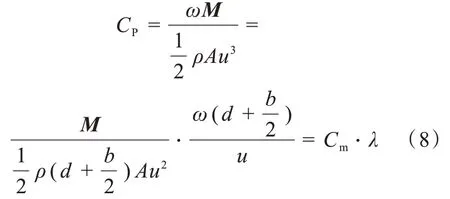
力矩系数与风能利用率呈正相关。因此，提高风力发电机启动力矩系数，可以优化其启动性能。

2.2 流动理论模型

风力发电机被来流推动旋转，时刻干扰流体的运动状态，且空气具有可压缩性和黏性，导致风力发电机中的流场复杂，但流体具有连续性，且一定时间内流入系统的空气遵循质量守恒定律，运用动量方程

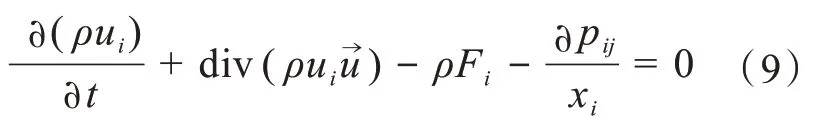
其中υ为运动粘度，+ div(ρuiυ)为单位体积上的惯性力。引入连续方程

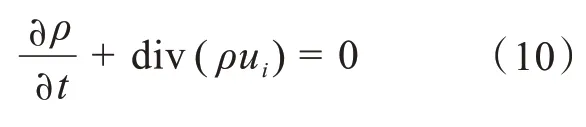
可以得到

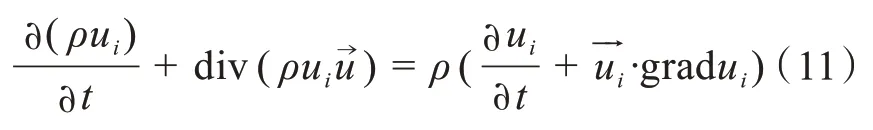
该方程适用的流体种类广泛，但流体不同，其物性参数也不同，即在同一温度下的不同可压缩流体的体积压缩或膨胀能力均不相同，同种可压缩流体在不同温度条件下的压缩及膨胀的能力也不同，根据式（5）将VAWT 视为一个系统，则系统做功和损耗的能量及系统与环境的能量交换呈守恒状态，故引入能量守恒方程

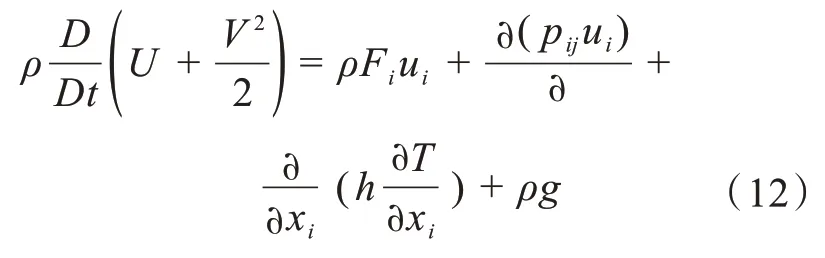
其中U为流体内能，V为流体体积，h为换热系数。联立可以发现未知数存在6 个，方程等式不足以求解未知量，故补充状态方程

根据黏性流体贴壁流动的特性，扇叶表面附着空气流动边界层，此时空气的流动状态呈层流流动状态。扇叶的弯曲性使扇叶具有导流的效果，改变空气的流动方向，且在H 型VAWT 中叶片存在气动载荷，将其引入源项S［8］，得到基于可压缩黏性流体的N-S 方程（RANS）对空气的运动场进一步描述：

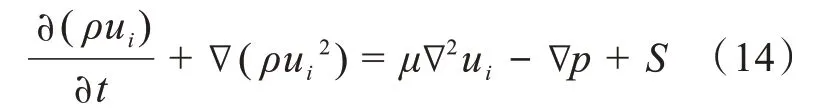
其中μ为动力黏度。由此可以得到整个流动域中流体的运动状态。

在计算流体力学（computational fluid dynamics，CFD）中，主要采用k-ε模型和k-ω模型对风力发电机进行求解，k-ε模型主要针对高雷诺数模型进行仿真计算，而k-ω模型主要针对低雷诺数进行仿真计算，由于空气贴壁流动状态为低雷诺数的层流状态，使得k-ε模型需要对边界进行修正设定，而k-ω模型则无需对边界进行处理。

湍流动能k-ω模型输运方程为：

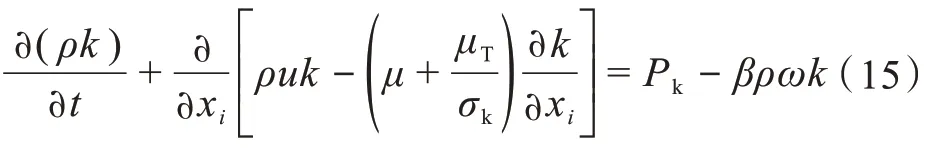
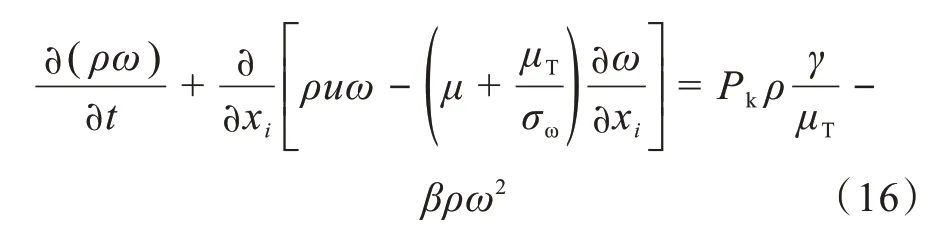
其中β，σk，γ和σω均为常数［9］，μT为模型涡黏性，β为流体的等温圧缩率，且

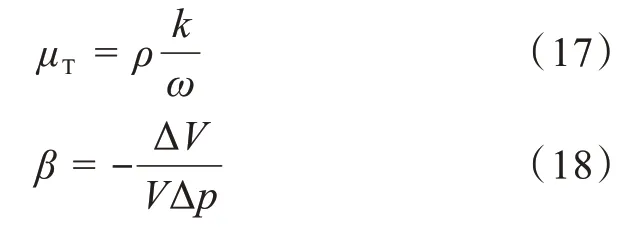
对于无滑移壁面边界的条件为：

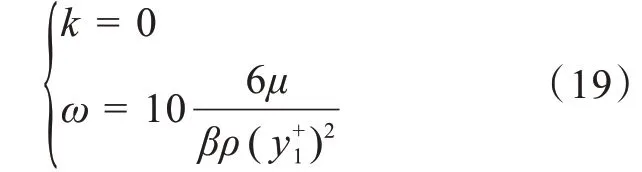
式中y1+代表第一个距离边界节点的参数，并且y+是划分网格的一个重要参数，其计算方程为：

式中uτ为流体与壁面接触产生摩擦时的速度，该式与雷诺数计算公式相似。

湍流中的流体存在大量的变形及多种应力，且流体本身的黏性在一定条件下对流场的变化同样有很大的影响。在FLUENT 中，剪切应力传输模型（shear stress transfer，SST）综合考虑了以上情况，使得SST 模型在流动边界层处的计算更为精确。本文研究对象为H 型与S 型结合的VAWT，需要考虑同时适用于两种叶型的湍流模型。文献将常规S 型VAWT 采用SSTk-ω模型和k-ε模型分别模拟计算得出的数据与1978 年的S 型VAWT 实验数据进行对比，发现SSTk-ω模型计算结果更适用［10-12］；有学者［8，13］研究后发现SSTk-ω模型的使用条件更符合H 型VAWT，计算出的结果更符合实际结果，并且SSTk-ω模型相较k-ε模型适用性更强［14］。综合考虑各个模型的使用条件后，发现本文的研究模型采用SSTk-ω更为适宜。

3 数值模拟设置

3.1 计算域模型

取实体截面进行模拟，且以H 型叶片为主研究对象，Savonius 叶片为参照对象。由于2 种叶片处于同一圆盘上固定，使得2 种叶片共同旋转运动，并且H 型叶片与S 型叶片旋转域的间隙较小，故H 型叶片不再以传统的H 型叶片旋转域进行划分，与S 型叶片划分于同一旋转域中，因此模型整体与传统Savonius VAWT 的计算域设置方式相同。

如图4 所示，以VAWT 转动中轴为原点，流域的上下边界施加无滑移壁面的条件，并且距x轴10d；流域中将左侧设为入口，流体水平流动10d距离开始对风力发电机作用；流域右侧设为出口，距y轴30d可以充分模拟出流体流过风力发电机后产生的涡流；旋转域设为顺时针转向，旋转域和流动域交界面为interface。

图4 边界设置示意图Fig.4 Boundary setting diagram

3.2 模型网格划分

网格划分采用ANSYS Mesh 进行划分，多边形在网格划分中被广泛使用，而多边形均可由三角形进行划分。三角化非结构网格无结构特性，适应性强，质量高。如图5 所示，旋转域至流域的网格数量存在一个渐变的过程，对旋转域进行网格加密处理，可以使计算更为准确，同时缩短计算步长，将流动域与旋转域的交界面网格尺寸设为一致，提高流动域及旋转域的网格连接准确度，使网格过渡更为平滑。S 型扇叶及H 型扇叶边界与流体存在一个层流的过渡区域，因此需要添加膨胀层，可以将叶片附近的流体运动状态描述精确，其层数设为10 层，因流体的流动状态与边界的距离存在一个线性关系，因此增长率设为1.2，并将叶片边界膨胀层进行加密，S 型叶片图形为规则图形，且狭窄部分为叶片重叠部分，因此需要保证重叠部分的网格精度。H 型叶片有一个狭小的弯头处，将膨胀层网格加密，使网格与弯头进行较好的贴合，提高H 型翼型的计算准确度。

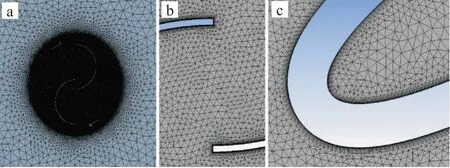
图5 网格划分：（a）旋转域，（b）S 型重叠处，（c）H 型前缘Fig.5 Meshing：（a）rotation domain，（b）S-type overlap，（c）H-type leading edge

3.3 计算设置

当来流对VAWT 作用时，风与其表面接触产生压强，与此同时，VAWT 对风存在一定的阻碍，使得流场变化，可以发现流体与叶片存在一定的耦合关系，采用COUPLED 算法，该算法联立大量的流体方程进行求解，计算相较其他算法更为庞大，但可以保证精确度，并缩短了收敛的计算步长。由于CFD 模拟计算结果与实际情况存在一定的偏差，故对不同的模拟对象采用相同的网格尺寸、方法和计算模型，对比得到的结果可在一定程度上减小误差，因此对S 型VAWT 与升阻混合型VAWT 采用相同流动模型并进行定常数值模拟对比。以θ= 0°为起始角度，间隔15°为一个模拟项目，针对θ=125°进行一次单独数值模拟，由于180°与0°扇叶状态相同因此不再对180°进行模拟，而对175°进行模拟，当叶片以0°启动时存在一定的误差，因此针对5°同样进行一次单独模拟，故每个模型进行15 组定常数值模拟。

4 结果与讨论

对静止的VAWT 进行定常数值分析得到启动力矩系数，启动力矩系数越大，代表其启动风速越小，如表1 所示。

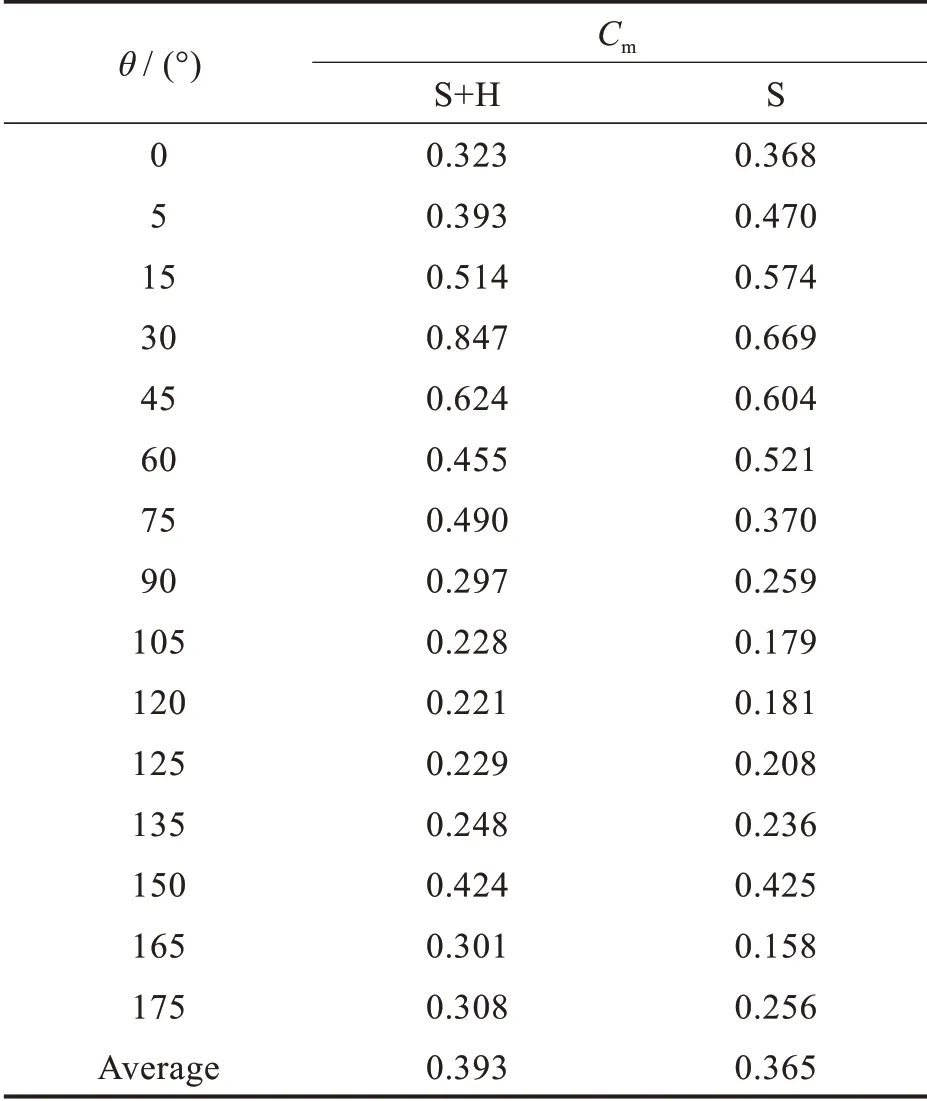
表1 静态启动力矩系数Tab.1 Starting torque coefficients

混合型VAWT 与传统S 型VAWT 的启动力矩系数峰值均处于30°附近且混合型VAWT 的启动力矩系数峰值相对传统S 型VAWT 提高了26.6%，最小值提高了27.4%，但混合型VAWT 在60°的启动力矩系数低于传统S 型VAWT；在125°时，混合型VAWT 的启动性能有所提高，启动力矩系数提高了10.1%；混合型VAWT 平均启动力矩系数提高了7.7%。

将数据绘制成曲线图，观察混合型VAWT 的启动性能变化趋势，如图6 所示，θ于0°～20°左右时混合型VAWT 启动性能低于传统S 型VAWT；θ于20°～43°附近时，混合型VAWT 启动性能更优，但在43°～65°附近时，混合型VAWT 处于一个较差的状态；在65°～175°中，θ于140°～150°时，混合型VAWT 略低于传统S 型，因此当θ∈［0°，20°），（43°，65°］，（140°，150°）时，混合型VAWT 启动性能低于传统S 型VAWT，由此可知，在一个周期内，混合型VAWT 初始角度启动性能优于传统S 型VAWT 的约占整个周期的71.1%。

图6 启动性能曲线图Fig.6 Starting performance curves

针对θ于43°～65°时混合型VAWT 启动性能低于传统S 型的情况，取60°及75°进行压力场及速度场对比分析。如图7 所示，θ处于60°时，H 型扇叶相较75°时对S 型扇叶遮挡的面积更大，导致S型扇叶接近旋转轴的部分压力高于扇叶外缘，而75°时S 扇叶整体受到的风压较大，S 型扇叶外缘压力越大，其转动性能越好，且60°时H 型扇叶受力情况较差；如图8 所示，75°时，上H 型扇叶的下表面流速远高于60°时的上H 型扇叶的下表面，从而表明60°时，H 型扇叶受力情况较差，且对S 型扇叶的性能影响较大。即θ于43°～65°时，有混合型VAWT 启动性能低于传统S 型的情况发生。