岩溶地区隧道突涌水机理的研究进展
2022-07-01冯雪冬周小龙胡亚晴
冯雪冬,周小龙,胡亚晴
武汉工程大学土木工程与建筑学院,湖北 武汉 430074
近年来,随着我国隧道工程的高速发展,在具有强岩溶、大埋深、高地压等特点的西南地区,隧道施工过程中时常发生突涌水灾害。国内外学者依据隧道突涌水灾害源类型[1]、影响因素[1-2]、发生条件[1]等,基于理论分析、试验研究和数值模拟[3-5]等方法,研究了隧道突涌水发生的力学机理和灾变过程。本文总结了国内外关于岩溶地区隧道突涌水机理的研究进展,综述了在不同灾害源类型下的突涌水灾害的发生机理,为岩溶地区隧道施工中的突涌水问题研究提供参考。
1 岩溶地区隧道突涌水灾害类型
在富水、高压条件下,由于岩溶地区复杂的地质结构和工程因素(如隧道开挖扰动)的影响,围岩稳定性被破坏,地下水及其他充填物涌出,故发生突涌水灾害[1]。李术才[6]依据灾害源类型将突涌水灾害划分为4 种基本类型:裂隙型、断层型、溶洞溶腔型与地下暗河型。表1 总结了不同灾害源类型下突涌水发生特征及简易示意图。

表1 不同灾害源条件下突涌水特征及示意图Tab.1 Characteristics and schematic diagrams of water inrush under different types of disaster sources
2 岩溶地区隧道突涌水机理研究现状
2.1 裂隙型突涌水机理
聂韬译等[7]研究发现裂隙劈裂演化的过程是原生裂隙填充物被冲刷→原生裂隙起裂、翼裂纹开始产生→翼裂纹扩展→形成劈裂破坏。文献[8]将裂纹简单划分为Ⅰ型、Ⅱ型、Ⅲ型裂纹,如图1 所示,具体特点如表2 所示。在实际工程中,张开型裂纹最重要;在地学中,剪切型裂纹则具有重要意义,复合型裂纹是由Ⅰ型、Ⅱ型、Ⅲ型裂纹两两组合或三种组合而成。

表2 裂纹简单分类及特点Tab.2 Simples classification and characteristics of cracks
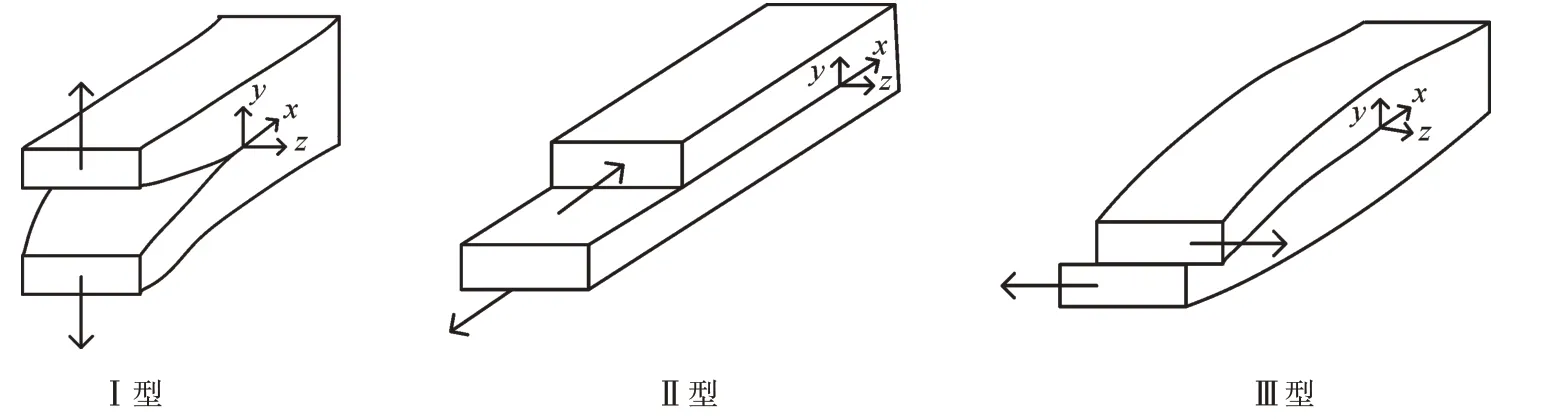
图1 裂纹的3 种基本类型(图中箭头表示相对运动方向)Fig.1 Three basic types of cracks(arrows in figure indicate relative direction of motion)
为便于数学处理,文献[7,9-10]将三维裂纹简化为二维裂隙岩体力学模型。如图2 所示:沿水平和垂直方向建立整体坐标系xoy,沿裂面和裂面法向方向建立局部坐标系x'oy',裂隙受应力σ1为最大主应力,σ3为最小主应力作用,裂隙面同时作用水压pw。假定水压沿各个方向作用力相等,将应力投射在局部坐标下的应力分量与水压pw相叠加,可求出裂隙面实际应力分量σn,τn。
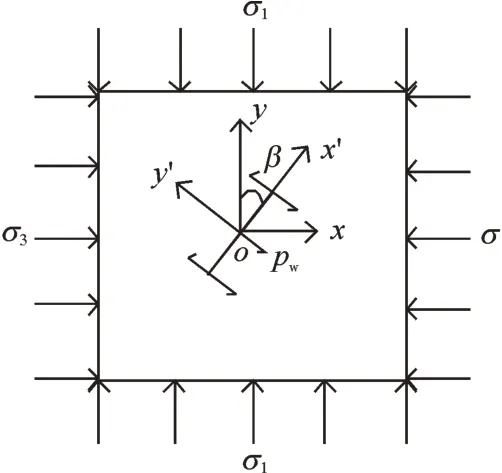
图2 裂隙岩体力学模型Fig.2 Mechanical model of fractured rock mass

根据式(1)可知,裂隙壁面上有正应力和剪应力,故裂隙处于I-II 复合型状态。由图3 可知,裂面法向应力方向(拉应力、剪应力)决定裂纹扩展方式。I-II 复合型裂隙的断裂判据主要有最大周向应力理论、最小应变能密度因子理论和最大能量释放率理论等,即表3。

表3 I-II复合型裂纹断裂判据计算公式Tab.3 Calculation formula of I-II composite mode crack fracture criterion

图3 拉剪复合型(左)和压剪复合型(右)Fig.3 Pull-shear composite(L)and press-shear composite(R)
文献[8,12]基于不同的裂纹扩展模式,推导出含有单裂纹、多组平行裂隙的岩盘最小安全厚度公式,提出岩盘防突厚度是判断岩盘是否失稳的重要准则[12]。
对于具有溶洞等大型含水构造且存在优势裂隙的岩体,郭佳奇等基于单裂纹起裂三区理论[8]、单裂纹起裂两带理论[2]推导出考虑外界水压力、地应力条件等的岩盘最小安全厚度计算公式(2)和公式(3)。
三区理论

两带理论
式(2)和式(3)中:h为隔水岩体安全厚度,h1和hc为施工引起的松弛厚度区,取1~3 m;hf为抗劈裂保护区厚度,当侧压力系数<1 时,用式(1)计算,否则,用式(2)计算;h3为裂隙带区厚度,利用雷达探测或者钻探验证;ΚIC为岩石I 型断裂韧度,ΚIIC为岩石II 型断裂韧度,常取1~3 m;pw为裂隙水压;β为裂纹与最大主应力之间的夹角;λ为原始侧压力系数;hz为隧道埋深。
平行裂隙常见于充水充泥岩溶构造中,适用裂隙发育的节理岩体,在式(2)和式(3)的基础上,文献[8,12]推导出具有多组平行裂隙的岩盘的最小安全厚度公式[式(4)]:
式中:lc=D/( 2 sinφ),D为断续节理排距;ΚIC=ΚIWlc,分支裂纹扩展至临界长度时尖端应力强度因子。
2.2 断层型突涌水机理
当岩体开始发生破裂,内部会出现微裂纹,随着时间的推移微裂纹逐渐发育成裂隙,累积到一定数量的裂隙形成一条明显的断裂面(断层两盘借以相对滑动的断裂面),一旦断裂面的应力差超过摩擦阻力时,两盘将开始相对滑动,最终形成断层[4,13]。断层由断裂带和断层盘组成,按照力学机制可分为张性和张扭性断层、压性和压扭性断层[6],具体特征见表4。
对于断层倾角及规模较大的未胶结的富水断层破碎带,孟凡树等[14]基于筒仓理论和极限平衡方法,并且忽略水对岩盘的水合作用影响且不考虑散粒之间的黏聚力,建立了断层与隧道轴线正交岩塞力学模型及断层与隧道轴线平行固支梁力学模型,推导出考虑断层破碎带的宽度、截面水力半径ρ的防突岩盘最小安全厚度理论公式(表5),表中断层岩盘所受地应力p计算公式如式(5)所示。

表5 断层型防突岩盘最小安全厚度计算公式Tab.5 Calculation formula of minimum safe thickness of fault-type outburst prevention rock plate

式中:γ为断层破碎带岩体容重,kN/m³;θ为断层破碎带倾角,°;μ为摩擦系数;ρ= 0.5bl/( )b+l,为截面水力半径;ΚZ为计算点处的埋深,m。
2.3 溶洞溶腔型突涌水机理
可溶性岩石因地下水对岩体的侵蚀作用而形成一定的地下空间称为溶洞。根据文献[15-18],在隧道开挖扰动作用下,岩体防突层厚度逐渐减小,当超过某一临界值,隧道将发生突涌水灾害,故岩盘的安全厚度是判断溶洞溶腔型突涌水是否发生的重要指标。在隧道施工过程中,溶洞溶腔的位置、形状及其大小、充填状况、充填物质种类等都会对其产生较大的影响。
对于岩盘力学模型符合小变形理论,并且简化开挖后隧道与溶洞之间的成拱效应的情况。于杰绪[15]考虑隧道不同位置的溶洞,基于强度理论将岩盘简化为各向同性、材质均一连续的弹性梁模型,推导出拱顶溶洞、底部溶洞、侧部溶洞、拱腰溶洞、拱脚溶洞与隧道间的岩盘安全厚度计算公式,具体力学模型及计算公式见表6。
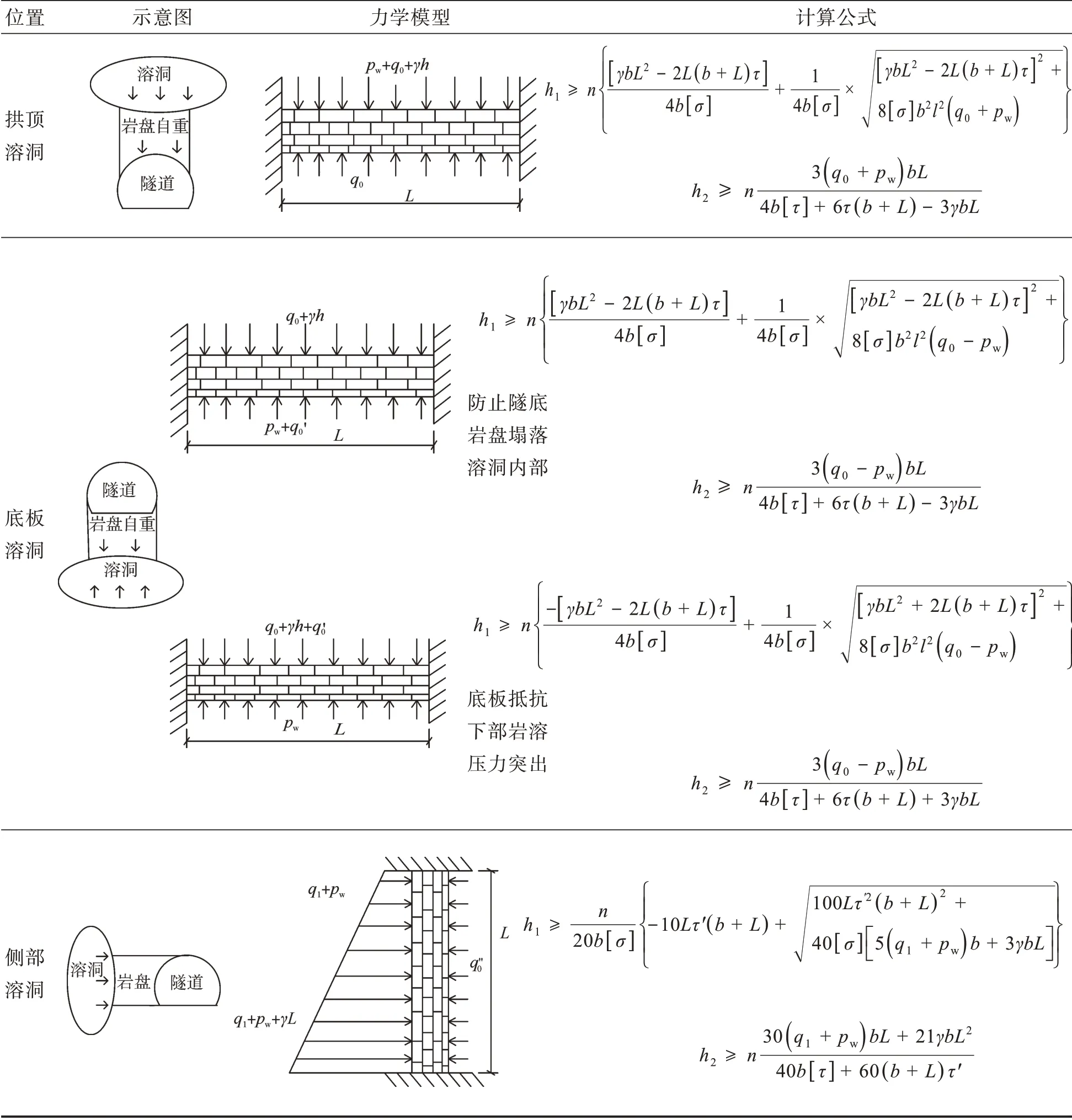
表6 隧道不同位置的溶洞溶腔力学模型及最小安全厚度hminTab.6 Mechanical models and minimum safe thickness(hmin)of Karst cavity at different positions of tunnel

续表6
位于隧道掌子面前方的溶洞,目前主要通过弹性梁、弹性薄板理论、弹性厚板理论、突变理论等方法建立力学模型[12,16-18],推导出隧道掌子面前方最小安全厚度的计算公式。
对于简单且较完整岩体,李利平等[12]将在水压力作用下掌子面前方的隔水岩层简化为固支梁力学模型,推导岩层最小安全厚度计算公式(6):

式(6)中:h为隔水岩层的安全厚度;pw为岩溶水压力;L为隧道直径;σt为岩体容许抗弯强度;n为修正系数,取0~1。
吴祖松等[16]基于统一强度理论和弹性薄板弯曲理论,推导出掌子面前方的岩层在简支[式(7)]和固支[式(8)]条件下的最小安全厚度计算公式:

式(7)和式(8)中:h为掌子面防突岩盘厚度;r为防突岩盘半径;b为统一强度理论中的权系数,不同取值可适应材料的不同屈服或破坏准则,一般情况下可取b=0、1/4、1/2、3/4 等;φ为内摩擦角;c0为剪切强度参数。
弹性板根据厚跨比的不同分为薄板和厚板,当岩溶隧道掌子面前方岩层厚度不能确定时,可采用弹性厚板理论[17]。郭佳奇等[2,17]基于弹性厚板理论,针对较完整掌子面前方的岩层,建立考虑拉破坏[式(9)]、剪切破坏[式(10)](岩层简化为圆形、正方形、矩形)下的最小安全厚度计算公式:

式中:h为防突岩盘厚度;σt为岩体的抗拉强度;γi为上覆第i层的容重,kN/m3;Hi为上覆第i层的厚度,∑Hi为岩墙中心埋深,m;D为隧道直径,m;ls为隧道断面边长,m;H、W分别为隧道高度、跨度,m;φ为岩体的饱和内摩擦角;c为岩体的饱和黏聚力,kPa。
对于较完整岩体且初等突变的岩层,孙谋等[18]将隧道简化为圆形,基于突变理论,推导出最小安全厚度计算公式[式(11)]:

式中:h为掌子面防突岩盘厚度;Δq为岩溶水压与隧道空气压力的压力差;E为岩板的弹性模量;a为圆形隧道的半径;μ为泊松比。
由式(6)~式(11)可知,隧道掌子面前方岩盘最小安全厚度和外部压力、岩盘自重等因素相关,但未考虑充水溶洞大于或小于隧道跨度的情况。聂一聪[19]和孙尚渠[20]分别利用突变理论和极限分析上限法,将隧道掌子面视为较完整的岩体,推导出岩盘最小安全厚度计算公式,具体示意图及力学模型见表7。

表7 位于隧道掌子面前方不同大小的溶洞溶腔示意图及力学模型Tab.7 Schematic diagrams and mechanical models of Karst cavity with different sizes in front of tunnel face
岩溶地区突涌水类型主要分为裂隙型、断层型、溶洞型三类[6]。主要基于断裂力学、弹性力学等理论构建力学模型,以岩盘安全厚度为主要指标,判断是否发生突涌水灾害,但实际施工环境较复杂,还需考虑土层特性、地质构造的形状与大小等因素。
3 基于数值模拟和试验模拟的隧道突涌水研究
数值模拟一般基于连续变形理论、非连续变形理论[12,21-22],运用有限元法、有限差分法、离散元法等方法模拟隧道突涌水灾害的演化过程[23-25]。突涌水灾害发生的判断依据有塑性区是否贯通、应力等物理量变化、颗粒启动速度、临界流速等[12],见表8。

表8 数值模拟方法及判断准则Tab.8 Numerical simulation methods and judgment criteria
杨艳、Bai 等[26-27]运用数值模拟对突涌水灾害过程进行了研究,发现除围岩强度、岩层产状、隧洞埋深等常见影响因素外,破坏点的水压力、岩层渗透性物理量、裂缝初始长度和起裂压力等因素对隧道突涌水过程均有不同程度影响。对于断层构造,其宽度也是影响隧道突涌水灾害过程的重要因素。赵宁[28]采用多场耦合软件基于理查德方程和达西方程研究发现含水层水压、断层宽度是隧道断层破碎带滞后突水过程的重要影响因素。对于溶洞溶腔构造,吴祖松等[16]将隔水岩层看作较完整的岩层,并通过研究发现溶洞位置、水压、侧压力系数、岩盘厚度等影响因素对围岩的位移场、应力场、塑性区等有重要影响。
关于突涌水现场试验和模型试验,国内外学者也开展了大量研究[29-31]。表9 总结了现场试验和模型试验的适用条件与优缺点,其中模型试验模拟突涌水灾害发生的判断准则有水压和应力的变化程度、充填物质的渗流速度、岩体的渗透系数等[12]。

表9 试验模拟分类及优缺点Tab.9 Classification,advantages and disadvantages of test simulation
孟如真等[32]通过现场高压压水试验研究发现岩体发生水力劈裂后,岩体的渗透特性急剧增大。周毅、Fu 等[33-34]开展流-固耦合模型试验,模拟了岩溶地区隧道突涌水的全过程(图4)。由理论研究可知,岩层防突厚度是判断隧道突涌水灾害是否发生的重要因素,例如李浪等[29]通过隧道掌子面前方突涌水灾害防突岩盘相似模型试验,进一步验证岩层防突厚度对掌子面突涌水灾害发生的重要影响。

图4 岩溶隧道突涌水过程Fig.4 Water inrush process of Karst tunnel
数值模拟和试验研究能够较好地分析在不同影响因素下岩体应力、位移以及渗流变化情况,但如何将复杂的工程地质模型概化还需要进一步研究。
4 结论与展望
本文针对目前隧道突涌水灾害发生机理的研究进展,重点介绍和分析了在不同灾害源条件下岩溶地区隧道突涌水发生机理及发生条件。
(1)概括了裂隙型、断层型、溶洞型突涌水灾害机理的研究进展。但是现有裂隙型突涌水机理研究主要针对I-II 复合型裂隙断裂,缺少关于其他复合型裂隙的研究;断层型突涌水机理研究考虑了基于断层破碎带的宽度、截面水力半径的影响,但是考虑因素单一,可进一步研究渗透失稳发生的临界状态和渗透失稳的发生条件;溶洞型突涌水主要将岩层看作较完整的岩盘,但是在实际工程中岩层存在不同发育程度的裂隙。
(2)针对隧道突涌水灾害发生的判断指标,总结岩层最小防突厚度的概念及不同类型下岩层最小防突厚度计算公式。但上述公式主要基于平面应力状态,与实际空间应力状态相差较大。故需要采用三维有限元分析或者试验模拟,对岩盘最小防突厚度等问题进行深入分析,建立考虑不同土质等条件下的岩层最小防突厚度公式。
(3)总结了数值模拟方法判别突涌水灾害发生的标准。但岩溶地区隧道突涌水的数值模拟和试验模拟大多研究的工况单一、影响因素较少,不能有效模拟岩体真实变化状态。
