基于贪心算法的板材多孔加工路径优化算法研究

吴焱明, 曹 宁, 李飞亚, 李 昂

(合肥工业大学 机械工程学院,安徽 合肥 230009)

0 引言

在板材生产过程中,对于多孔板材的攻丝加工是最耗时的一道工序。金属板材上各孔的攻丝顺序直接影响加工时间,只有合理规划攻丝加工路径,才能缩短刀具行程、提高加工效率。自动攻丝机在板材生产行业应用比较广泛,但存在加工时间长、效率较低等缺点。对于大型金属板材的攻丝加工,由于不同的板材螺纹孔规格有M3～M10不等,加工过程中需要更换刀具,但因为更换刀具必须要回到刀具的参考点,所以可以将每一类螺纹孔的加工看作是同一类问题。因此，对自动攻丝机同一规格螺纹孔的加工路径进行优化,能减少总加工时间、提高经济效益。

攻丝机在一次加工完成后,刀具需要回到起点,加工路径是一个回路,这等同于旅行商问题(traveling salesman problem,TSP)。TSP问题是经典的NP-hard问题,可以简单描述为:一个商人在地图的一系列城市中访问,求解访问每座城市一次并回到起点的最短路程。TSP问题有着广泛的应用,如数控加工、无人机路径规划、机器人路径规划、物流配送、网络通讯等。TSP问题是一个NP完备问题,其解空间存在“组合爆炸”,10个城市的TSP有大约18 000个可能的解,因此,要得到10个城市TSP问题的最短路径,最坏的可能是要做18 000次搜索;20个城市的TSP问题,最坏可能要做1016次搜索;50个城市的TSP问题搜索次数更是一个天文数字。目前,关于TSP问题的解决方案有很多,对于孔群加工而言,现有的TSP问题解决方案大多以改进遗传算法[1-5]和改进蚁群算法[6-10]为主。文献[1]提出了改进遗传算法,以408个孔的大型轮胎模具孔群加工为例,遗传算法的平均运行时间为10 547.475 s,改进遗传算法的平均运行时间为3 839.202 4 s;文献[2]提出了改进蚁群算法,用82个无规律孔的冲压板做实验,基本蚁群算法的平均运行时间为91.311 7 s,改进蚁群算法的平均运行时间为30.730 9 s。在板材多孔加工中,螺纹孔的数目比较庞大,少则几十,多则成百上千。在这种规模的问题中,现有的解决方案搜索时间太长,根本无法满足生产要求。攻丝机的路径规划不需要一定求出最优路径,但必须在短时间内求出在一定范围内的最优解,如果路径优化所消耗的时间比刀具走过其缩短的路径所需要的时间还长,那么这将没有应用意义。

基于此,本文以攻丝机加工路径为研究对象,建立以最短路径为优化目标的数学模型。为提高算法效率,针对实际生产中常见的单一规格螺纹孔的金属板材孔位分布形式,采用不同的策略进行分组,运用贪心算法进行路径规划生成最短路径,减少加工时间。

1 模型建立

攻丝机进行攻丝加工的路径规划问题可描述为:二维平面上有n(n≥1)个螺纹孔需要加工,各孔的圆心记为Pi,圆心坐标为(xi,yi)，i=1,2,…,n。各孔的集合记为A={P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)}。在实际生产中,攻丝机的横向和纵向最大移动速度相同,因此本文在计算路径长度时采用切比雪夫距离(Chebyshev distance),即孔间距取两孔横坐标和纵坐标数值差绝对值的最大值。金属板材螺纹孔i和螺纹孔j间的长度Dij为:

Dij=max(|xi-xj|,|yi-yj|)

(1)

攻丝机的刀具需要找到一条从任意一孔的圆心Pi出发,途中经过每个孔圆心的路径,并使总路径长度L最短,则L为目标函数。

2 算法分析

文献[3]中将贪心算法、基本蚂蚁算法以及改进的蚂蚁算法进行了比较,选取TSPLIB中的eil51数据进行实验,贪心算法耗时17 ms,基本蚂蚁算法耗时8 035 ms,改进蚂蚁算法耗时12 158 ms。由此可见,贪心算法在TSP问题求解中运算速度非常快。

在对问题求解时,贪心算法总是做出在当前看来最好的选择。也就是说,不从整体最优上加以考虑,而是求出在某种意义上的局部最优解。贪心算法解决问题效率高,时间复杂度低,其基本思想是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保能获得局部最优解。在板材多孔位加工中,板材的规格较大(一般为2 m×4 m),螺纹孔数目也较多,少则几十,多则成百上千,而且可能有些区域孔位分布比较密集,有些区域孔位分布比较稀疏。由于贪心算法的特点是不从整体最优上加以考虑,而是求出在某种意义上的局部最优解,结合板材孔位分布特点,在进行路径规划之前,先对板材上的螺纹孔群进行分组。因为实际板材的孔位分布不尽相同,本文提出对螺纹孔进行一维分组和二维分组。一维分组为按X坐标分组或按Y坐标分组;二维分组为按X坐标分组后再按Y坐标分组或按Y坐标分组后再按X坐标分组。在分好的每一组内采用贪心算法求出每组的最优解,最后将每一组的路径连接起来得到全局加工路径。

由于孔位分布的不同,按照不同方向进行路径规划结果差异明显。本文结合分组策略,在路径规划中定义2种路径法，即XY向路径法和YX向路径法。XY向路径法为:一维分组中按X坐标分组后组内按Y坐标进行排序或采用贪心算法;二维分组中按X坐标分组后再按Y坐标分组,组内采用贪心算法。YX向路径法与XY向路径法相反。

下面以尺寸为732 mm×3 570 mm且分布220个M6的待加工螺纹孔板材为实例进行验证。

2.1 一维分组后按坐标排序

考虑到在实际生产中,有一些金属板材的螺纹孔分布呈比较规则的矩形阵列,或者孔位分布比较密集,因此可按阵列规律,采用简单易行的方法进行加工路径的规划,即一维分组后按坐标排序。

首先,根据攻丝机刀具的起点位置建立板材加工的坐标系,刀具起点位于坐标原点;其次,根据建立的坐标系对螺纹孔按X轴或Y轴坐标进行排序;最后，根据排序结果继续按X轴或Y轴方向进行分组,组间距为50 mm,组内按照Y坐标或X坐标进行排序,这样可以将问题规模进行分解,分成若干个小规模问题进行求解。此算法的路径规划仿真结果如图1所示。XY向路径法的加工路径长度为27 776.0 mm,YX向路径法的加工路径长度为27 428.9 mm。

图1 一维分组后按坐标排序的加工路径仿真结果

2.2 一维分组后采用贪心算法

在实际生产中,板材螺纹孔的分布并不都是矩形阵列,采用按坐标分组排序得到的路径不适用于所有板材多孔位加工,因此需要对上述排序方法进行优化。

将螺纹孔按X坐标或Y坐标进行排序分组,组间距仍为50 mm,在每组内采用贪心算法进行排序。此算法的路径规划仿真结果如图2所示。XY向路径法的加工路径长度为23 191.6 mm,YX向路径法的加工路径长度为28 503.5 mm。

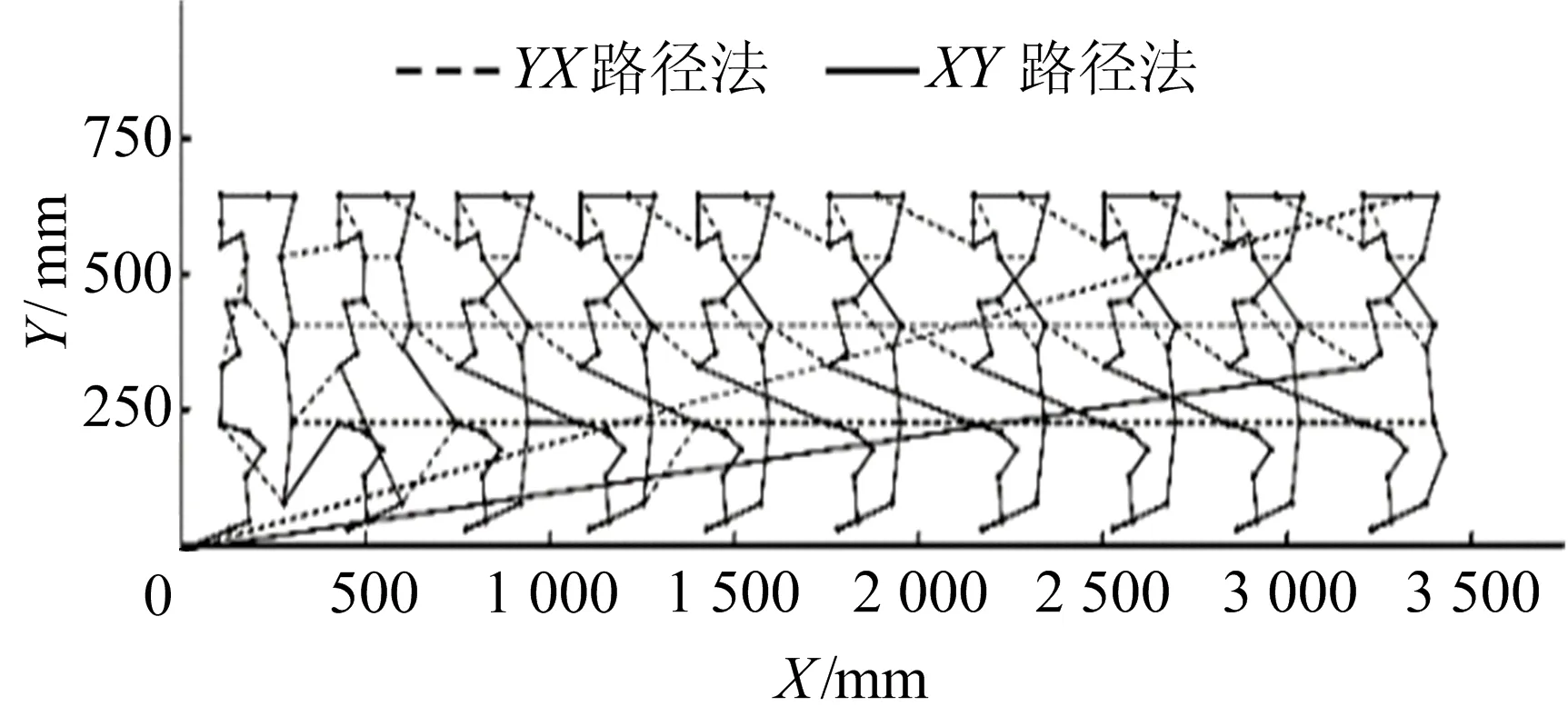
图2 一维分组后采用贪心算法的加工路径仿真结果

2.3 二维分组后采用贪心算法

考虑到对孔群一维分组后每组的待加工螺纹孔数目依然很多,不能更好地发挥贪心算法的优势,因此在对孔群按X坐标或Y坐标分组后,在组内对孔群再按Y坐标或X坐标分组,X方向和Y方向的组间距均为50 mm。这样将金属板材上的所有螺纹孔分为若干个矩形方块,即网格状,故称为二维分组或网格化分组。将孔群二维分组后,在每个网格内采用贪心算法进行排序。此算法的路径规划仿真结果如图3所示。XY向路径法的加工路径长度为23 554.4 mm,YX向路径法的加工路径长度为22 257.5 mm。

图3 二维分组后采用贪心算法的加工路径仿真结果

3 路径优化

以上3种方法所得到的路径长度不同,见表1所列。

表1 不同方法及路径法得到的路径长度 单位:mm

由表1可知:XY路径法中二维分组后采用贪心算法所得到的路径长度比一维分组后按坐标排序得到的结果缩减了15.2%,比一维分组后采用贪心算法得到的结果增加了1.6%;YX路径法中二维分组后采用贪心算法得到的路径长度比一维分组后按坐标排序得到的结果缩减了18.9%,比一维分组后采用贪心算法所得到的结果缩减了21.9%;一维分组后按坐标排序YX路径法比XY路径法路径长度缩减了1.2%,一维分组后采用贪心算法XY路径法比YX路径法路径长度缩减了18.6%;二维分组后采用贪心算法YX路径法比XY路径法路径长度缩减了5.5%。

由此可以得出,在相同路径法下不同方法所得到的路径结果差异非常大,同样,相同方法不同路径法所得到的路径结果差异也非常大。因此,路径优化需要寻找最优方法和路径法组合,使得路径长度最短。

以上分析是建立在组间距一定的情况下,下面讨论组间距对路径结果的影响。

在实际生产环境中,板材上面的螺纹孔一般比较密集,如果组间距的取值大于临界值时,那么分组时会将所有的螺纹孔分到一组,而此临界值不会太大。上述每种算法耗时都在加工要求范围内,因此在按坐标分组时采用一维搜索的方式寻找最优组间距,在网格化分组时采用二维搜索的方式寻找最优组间距。组间距从初始值20 mm开始搜索,增量为10 mm,搜索终止条件为该方向的分组结果为一组。

在搜索过程中,组间距的某些取值可以使得上述算法得到的加工路径总长最短。相较于路径优化所带来的效果,优化过程的时间开销可以忽略不计,通过搜索最优组间距使得算法最终取得了良好的效果。一维分组和二维分组优化后的加工路径仿真结果如图4所示。

图4 经过优化后的路径结果

一维分组和二维分组优化后的路径长度和耗时见表2所列。

表2 路径优化结果及耗时

一维优化路径是按X坐标分组后采用贪心算法且X坐标组间距为340 mm的情况,路径长度为21 796.3 mm;二维优化路径是X坐标组间距为50 mm、Y坐标组间距为80 mm且采用YX路径法的情况,路径长度为19 832.3 mm。因此最优路径为二维优化路径。在相同方法和路径法条件下,最优路径长度比初始路径长度(即组间距为50 mm时的路径长度)缩减了10.9%,而优化总耗时最多不会超过1 s,由此可见路径优化取得了显著效果。

在路径优化之后,自动攻丝机的整体路径规划算法基本完成,前面的仿真结果还需要进一步在生产现场进行测试验证。自动攻丝机在实际加工时界面上只显示最优路径,刀具按照最优路径进行攻丝操作。

实际加工时的界面如图5所示,其中所显示的最终加工路径与仿真时对比得到的最优路径一致。

图5 自动攻丝机加工界面

4 结论

本文以自动攻丝机的加工路径为研究对象,提出3种不同的排序算法对孔群加工进行路径规划。第1种有针对性地解决了排列规则的金属板材路径规划问题,且简单易行,另2种基于贪心算法对加工路径进行优化,缩短了加工时长，提高了加工效率。最后通过对分组参数进行寻优,对算法进一步优化,最终在一定程度上找到了最优路径。通过仿真以及现场测试得出以下结论：

(1) 在实际生产中,一部分板材的孔位分布呈矩形阵列,孔位分布密集且相互之间距离相差很小,此时采用简单分组后按坐标排序的方式进行路径规划,简单易行且效率高。但考虑到加工方位的影响,对比2种方位分组排序结果,取路径最小者为实际加工路径。

(2) 对于非矩形阵列分布的金属板材,在分组后采用贪心算法对加工路径进行优化,从而减小路径长度，缩短加工时间。

(3) 为了充分发挥贪心算法的优势,将孔群第1次分组后按另一坐标再进行分组,即将金属板材上的孔群划分为网格状,然后采用贪心算法进行路径规划,进一步缩减路径长度。

(4) 通过对分组参数的分析,经搜索最优组间距,得到的最终加工路径相较于优化前的结果缩减明显。

本文研究结果对机械加工中的零件和板材的制孔以及攻丝路径规划有一定的参考意义,算法易于理解、优化,适应性强,运行速度快,能够大幅度提高加工效率。