文丘里分流器的结构优化与分配特性研究

胡远洋, 江 斌, 江文彬, 张文成

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

两相流的均匀分配广泛存在于化工、核能、动力等工业领域[1],无论是对于锅炉、加氢反应器[2]等大型设备,还是对于空调蒸发器这种小型设备,都需要将两相流体均匀地分配到各个管路[3]。影响两相流分配的因素有很多,下游各分支的间距[4]、分配器的几何因素[5]、入口质量流量、入口含气率[6]等均会影响两相流的分配,宏观上可将以上因素分为结构因素和非结构因素。对于各工业领域和日常生活中必不可少的换热器来说[7],在进行多支路设计以提高其换热效率时,两相流体均匀分配的问题便显现出来[8],此时,在换热器前增设分流器则成为解决两相流体分配不均的途径之一。

分流器按分配方式的不同可以分为分相式分流器和混相式分流器[9]。近年来关于分流器的研究很多。文献[9-10]各提出了一种新型分流器并应用于制冷系统中;文献[11]研究了不同工质在不同分流器中的分配特性;文献[12]研究了安装角度对分配效果的影响;文献[13]通过入口流型的调整实现了均匀分配。同时,随着计算流体力学的发展,计算流体动力学(computational fluid dynamics,CFD)被广泛地应用于两相流计算和分流器的设计[14],如文献[15-17]均通过CFD计算给出了各分流器的优化方案。

文丘里分流器[18]属于混相式分流器,也是目前工程中使用最为广泛的分流器之一[9]。本文就文丘里分流器在空调工况下的两相分配中,其收缩段型线等结构因素和入口干度等非结构因素对分流性能的影响做了相关研究,旨在得到结构的优化方案以及相关非结构因素对其分流效果的影响规律。

1 仿真模型

本文采用标准k-ε湍流模型和欧拉两相流模型对两相流分配进行仿真。为验证模型的可靠性,先对两出口分流器进行仿真,通过比较仿真结果与文献[19]的实验结果是否一致来验证所选模型能否预测气液两相流在分流器中的分配。两出口分流器结构示意图如图1所示。

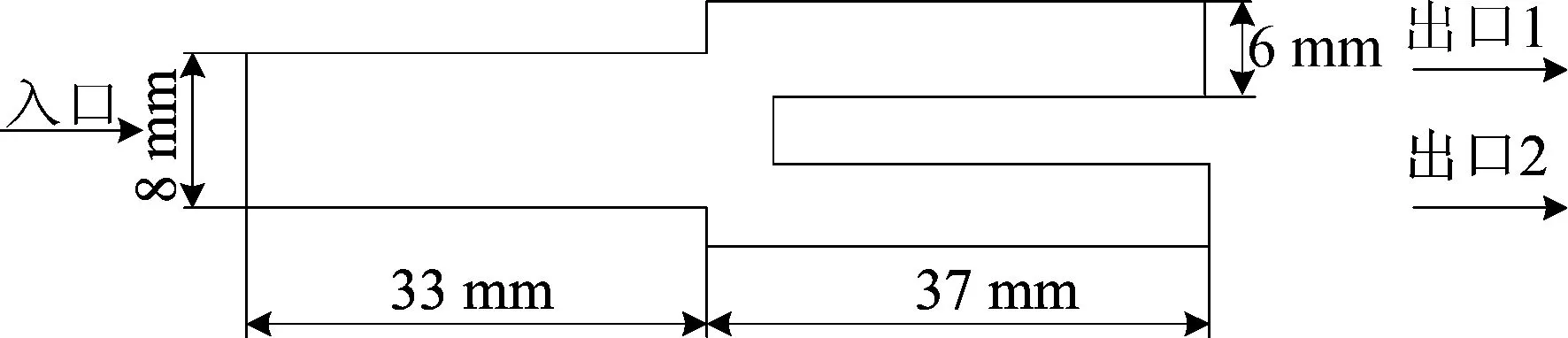
图1 两出口分流器结构示意图

文献[19]通过实验研究了入口气液流速的快慢组合及分流器与水平方向的夹角对图1所示分流器分流性能的影响,并以RG、RL来衡量分配的均匀性。

RG、RL的具体定义为:

(1)

(2)

其中:QG1为出口1空气的体积流量;QL1为出口1水的体积流量;QG2为出口2空气的体积流量;QL2为出口2水的体积流量。体积流量单位均为m3/s。

对RG、RL来说,上限均为1,下限均为-1,且RG、RL越接近0,两相分配越均匀,且在同一角度下,RG、RL随着气液流速的增加而趋近于0；当与水平方向夹角远离90°时,RG、RL更远离0[19]。显然RG、RL的变化趋势与进口气液流速的组合和倾角有关。

根据两出口分流器公开数据,本文选取了20组入口气液流速不同、与水平方向夹角不同的工况对该分流器进行仿真,通过比较仿真所得的RG、RL随工况点的变化趋势与实验是否一致来验证模型的可靠性。

为保证计算速度和精度,通过icem网格划分平台建立该分流器的二维模型并进行网格划分,采用结构化网格,网格数量为80 000,网格质量为1。仿真采用标准k-ε湍流模型和欧拉两相流模型,壁面函数采用Standard Wall Functions,其他常数(Fluent控制面板参数)见表1所列。

表1 k-ε模型相关常数

入口为质量流量入口,由气液流速计算得到各工况下的入口气液质量流量;湍流强度为5%,湍流直径为8 mm；两出口为压力出口，通过监测两出口的气液体积流量,计算得到各自对应的RG、RL。入口气液质量流量的计算公式为:

(3)

(4)

其中：Qm-l为液相质量流量,单位kg/s;Qm-g为气相质量流量,单位kg/s;vl为液相流速,单位m/s;vg为气相流速,单位m/s;d为入口直径,本例为0.008 m;ρl为液相密度,本例为水,值为998.2 kg/m3;ρg为气相密度,本例为空气,值为1.225 kg/m3。

将仿真计算结果与已有的实验值进行对比,结果如图2所示。

由图2可知,虽然部分点仿真计算的RG、RL与实验值有所出入,但总体来看,随着入口气液体积流量和分流器倾斜角度的变化,通过仿真计算得出的RG、RL变化趋势与实验结果相同,即仿真所预测的气液两相在该分流器中的分配随工况的变化与实验结果一致,故标准k-ε湍流模型和欧拉两相模型可以预测气液两相流在分流器中的分配。

图2 RG、RL仿真值与实验值的对比

2 分流效果的影响因素分析

文丘里分流器是一种混相式分流器,其结构示意图如图3所示。

图3 文丘里分流器结构示意图

两相制冷剂从入口端进入,随着截面积的减小,两相制冷剂降压增速,在喉部位置,流速达到最大再分配到各出口管。

本文通过相关专利[18]和市场调研确定该分流器基本参数为:入口直径D1=10 mm;喉部直径D2=4 mm;各出口管与中心线夹角α=30°;出口管直径d=2 mm;收缩段长度L1=5 mm;出口管管长L2=20 mm。

影响分流效果的因素可分为结构因素和非结构因素。结构因素之一是收缩段型线,如图3所示。型线有3种,3种型线的几何区别是型线前半部分收缩速度比后半部分快的程度,从大到小依次为型线1、型线2、型线3,其中型线3为直线,即从入口截面到喉部截面的收缩速度始终相同;另一结构因素是各出口管与中心线的夹角α。非结构因素是入口制冷剂的质量流量和干度。

2.1 相关假设

(1) 在制冷循环热力计算中,除过热和过冷外,其余过程与理论循环相同。

(2) 节流后的两相制冷剂为均匀的气液混合物。

(3) 制冷剂在分流器中的分配过程与外界无热量交换。

2.2 分流效果的评价

分流器的性能是通过各出口的质量流量之间的差异大小来体现的,考虑到本文涉及不同的质量流量,因此在标准差公式的基础上,让每个qmi与qm-ave相减后,再除以qm-ave,这样可以有效消除因质量流量不同而在不均匀度评价上带来的影响。不均匀度ε的表达式为:

(5)

其中:n为出口管数目,本文n=4;qmi为各出口管的制冷剂质量流量,单位kg/s;qm-ave为各出口制冷剂质量流量平均值,单位kg/s。

由(5)式可知,ε越小,各出口的质量流量之间的差异越小,即分流性能越好。

2.3 计算工况及边界条件

制冷工质选取R22,蒸发温度7 ℃,冷凝温度45 ℃,过热度5 ℃,过冷度5 ℃。在MATLAB中建立该循环的模型并计算得到该循环下分流器的入口制冷剂质量流量和干度,通过REFPROP9.0查到R22在7 ℃的物性参数。其中:气相密度ρg=26.344 7 kg/m3,气相动力黏度μg=1.166 5×10-5Pa·s;液相密度ρl=1 257 kg/m3,液相动力黏度μg=2.001 3×10-4Pa·s。

分流器入口采用速度入口,气相为第一相,液相为第二相,通过计算分别得到入口制冷剂流速v和液相体积分数Vvol,湍流直径为10 mm,湍流强度为5%,出口均为压力出口,计算模型采用标准k-ε湍流模型和欧拉两相流模型。

制冷剂入口流速v和分流器入口液态制冷剂体积分数Vvol的计算公式为:

(6)

(7)

其中:qm为制冷剂质量流量,单位kg/s;ρm为两相制冷剂的密度,单位kg/m3;ρg为气相制冷剂密度,单位kg/m3;d为分流器入口直径,本例为0.01 m;x为制冷剂入口干度。

2.4 网格划分及无关性检验

通过DesignModeler建立文丘里分流器的三维模型,再通过Mesh网格划分平台对其进行网格划分,如图4所示。该分流器有4个出口,为保证网格质量和计算速度,采用混合网格。

图4 计算区域网格

对采用型线2、α=30°的分流器在不同网格数下的不均匀度进行仿真计算以进行无关性检验,网格无关性检验结果如图5所示,最终确定网格数量为2.75×104。

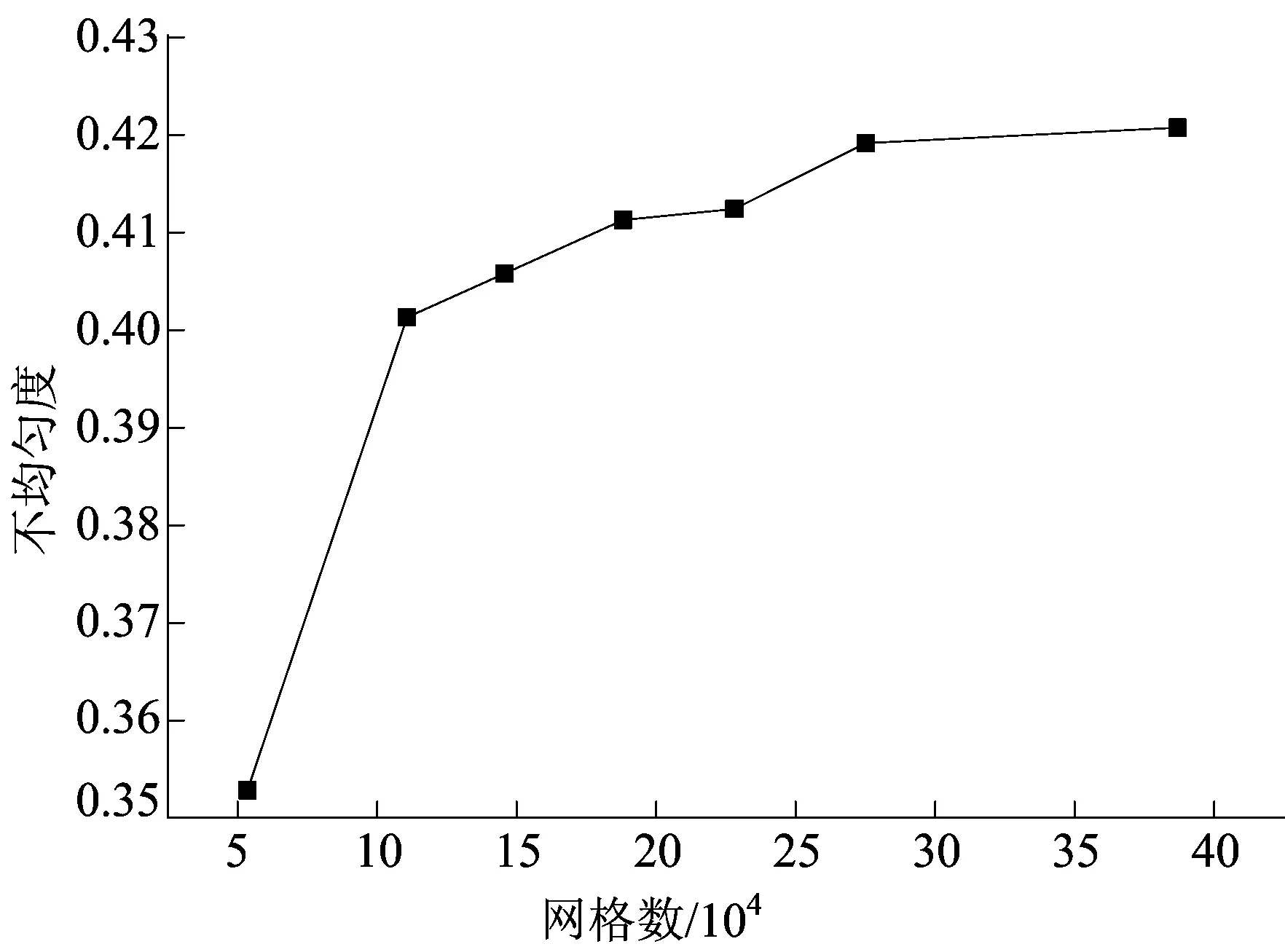
图5 无关性检验

2.5 仿真及结果分析

本文所研究的结构因素包括型线和出口管与中心线的夹角α(图3)。其中:型线有3种,出口管与中心线的夹角α包括从20°～75°的12种角度。

本文研究的非结构因素包括入口质量流量和干度。其中:质量流量的变化范围为45.58～113.96 kg/h;通过调整制冷循环中的过冷度改变分流器入口干度,当过冷度依次为2、5、8 ℃时,入口干度依次为0.227 6、0.207 3、0.187 4。

2.5.1 入口干度和夹角对分流效果的影响

在入口质量流量为68.38 kg/h、3种不同干度的情况下对使用型线2的12种夹角的分流器进行了仿真和不均匀度计算,不均匀度随夹角和干度的变化规律如图6所示。

图6 不均匀度随夹角和干度的变化

由图6可知:在入口干度相同的情况下,随着夹角的增加,分流器不均匀度均呈先降低后升高的趋势,分流效果最差的夹角是20°,分流效果最好的夹角是60°;当夹角在60°以上继续增加时,不均匀度急剧增大,因此各出口管与中心线夹角α的最优值为60°;当出口管与分流器中心线夹角由30°变为60°时,各干度下的不均匀度依次下降了19.25%、18.19%、16.97%;同时可以看出,各出口管与中心线夹角对分流效果的影响随着干度的降低而降低。

另一方面,在同一夹角下,不均匀度随着干度的降低而减小,随着入口干度从0.227 6降低到0.187 4,各角度下的不均匀度下降了13.95%～16.83%。

因此，对文丘里分流器而言,入口制冷剂干度越低,分流效果越好,在本工况下,入口干度每减小0.04,不均匀度则降低15%左右。

2.5.2 收缩段型线对分流效果的影响

家用空调器制冷量一般为2～3 kW,将制冷量2 kW和3 kW分别代入MATLAB,计算得到制冷剂流量为45.58 kg/h和68.38 kg/h。

将2种流量和上述3种干度组合成6种工况,各种工况下的入口质量流量以及干度见表2所列。

表2 各工况下的入口质量流量和干度

对出口管与中心线夹角α=30°的3种型线的分流器进行仿真,得到不同工况下各模型的不均匀度如图7所示。

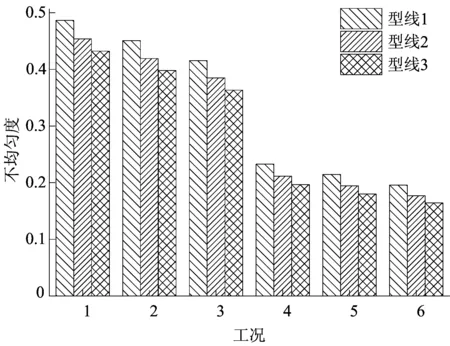
图7 不均匀度随型线和工况的变化规律

从图7可以看出,在所有工况下,不均匀度从大到小依次是型线1、型线2、型线3,且从工况1到工况6,型线3的不均匀度比型线2的不均匀度分别低了4.78%、5.09%、5.56%、7.04%、7.47%、7.20%。

因此,对于文丘里分流器而言,在入口直径和喉部直径固定时,采用收缩速度不变的型线3可以使分配不均匀度降低。考虑到工程实际中采用型线3可能会导致出现尖点从而增加局部流动阻力,在实际加工时可以通过小圆弧连接收缩段与喉部，从而减小产生的流动阻力。

从图7还可以看出,在2种流量下,不均匀度均随着干度的减小而降低。3种结构在质量流量为45.58 kg/h时,干度每减小0.04,不均匀度分别降低14.61%、15.22%、15.92%;在质量流量为68.38 kg/h时,干度每减小0.04,不均匀度分别降低15.93%、16.31%、16.45%。

2.5.3 优化方案及质量流量对分流效果影响

通过前2节的研究可知,在影响文丘里分流器性能的2个结构因素上,最优值分别是型线3和60°夹角,下面对这2个因素进行组合研究。

在入口制冷剂干度为0.207 3时,质量流量分别为45.58、68.38、91.17、113.96 kg/h的4种工况下对以下4种结构的分流器进行仿真。

(1) 结构一。采用型线2,α=30°。

(2) 结构二。采用型线2,α=60°。

(3) 结构三。采用型线3,α=30°。

(4) 结构四。采用型线3,α=60°。

各结构在不同质量流量下的不均匀度如图8所示。

图8 不均匀度随质量流量和结构的变化规律

从图8可以看出,相较于结构一,其余3种结构在相同工况下的不均匀度均低,且结构四的不均匀度相较于结构一下降得最多;在4种不同的质量流量下,相较于结构一,结构四的不均匀度分别下降了26.58%、28.60%、29.15%、29.32%。因此,文丘里分流器结构上的优化方案最终确定为夹角α为60°、收缩段采用收缩速度不变的型线3。相较于结构一，优化后的结构不均匀度能降低28%左右。

从图8还可以看出,4种不同结构的分流器不均匀度均随着质量流量的增加而迅速减小。对于结构一和结构四,当质量流量从45.58 kg/h增加到1.5倍时,不均匀度分别降低了53.61%、54.89%。

由此可见,入口质量流量的增加可以较大程度地减小文丘里分流器的分配不均匀度。

3 结论

(1) 在结构因素上,文丘里分流器各出口管与中心线的夹角和收缩段型线对其分配效果均有影响,各出口管与中心线夹角宜为60°,收缩段型线宜为直线。为避免工程中尖点的出现带来局部流动阻力的增加,在加工时可在收缩段型线末端采用小圆弧连接收缩段与喉部来减小流动阻力。

(2) 在非结构因素上,入口制冷剂质量流量和干度均会影响文丘里分流器的分流效果。入口干度越小,入口质量流量越大,分流效果越好，且入口质量流量的小幅增大可以使不均匀度有较大幅度的下降。

(3) 文丘里分流器的优化方案为增大各出口管与中心线的夹角为60°,同时采用直线作为收缩段型线。该优化方案相较于结构一,不均匀度能降低约28%。