基于时间感知的动态组旅行查询

李艳红，欧昱宏，毛德权，庞栩

（1 中南民族大学 计算机科学学院，武汉 430074；2 重庆市公安局 渝北区分局，重庆 401120）

1 问题的引入

随着智能移动终端的应用，以及地理位置与文本数据的融合，大量的空间文本对象应运而生，但仅考虑空间文本相似度的空间关键词查询有时无法满足成员的特殊需求.例如一组成员在晚上10点想要查询一家能同时供应中餐和西餐的餐厅，但大部分餐厅此时已经暂停营业，若仍用传统的查询算法，返回的结果很可能不是成员所需要的.

如今，为分散在各地的人们规划出最佳行程，不仅包括成员所需访问的不同类型兴趣点的查询，也要基于满足约束的兴趣点规划出最优路径.例如，图1显示了一个Euclidean空间中的TDGTP（Time Dynamic Group Travel Planning）查询，其中 3 个成员u1、u2和u3的起始位置和目标位置分别为（s1，d1）、（s2，d2）、（s3，d3）.成员 u2和u3需要找到一家能同时满足牛排和汉堡这两个关键词的餐馆，然后成员u1与他们在音乐厅碰面去听音乐（蓝线所示），听完音乐后成员u3直接回到家中（绿线所示），其余成员则去书店买书，最后回到各自的家中.通常会遇到满足关键词要求的兴趣点邻近小组中的某位成员，但距离组内其他成员较远的情况，此时该行程规划可能不是最佳路径.为此，希望找到满足该组成员要求且总行程距离最小的最佳路径，其中总行程距离是组中所有成员的行程距离之和，每个成员的行程从起始位置开始，然后访问满足要求的兴趣点，最终到达目标位置，结束行程.

图1 一个TDGTP场景Fig.1 A TDGTP scene

当前研究人员并未考虑行程规划中新成员加入或已有成员离开的问题，也没有在行程规划中考虑兴趣点与查询需求的时间匹配问题.因此，本文提出了一个新问题——时间感知的动态组旅行规划查询（TDGTP）问题.上述示例中有待解决的问题有：

（1）在兴趣点数量庞大的空间中，如何修剪掉不满足要求的兴趣点，快速找出符合所有成员要求的兴趣点区域？

（2）对于一组成员的旅行规划，怎样才能找出符合所有成员要求的兴趣点？

（3）如何使该行程的总距离达到最小，返回一个最佳路径序列？

为应对上述难题，本文提出以下解决方案：首先将R-Tree 与倒排文本列表和时间文本列表结合，构建了TIR-Tree 索引结构及相关算法KMA（Keyword Matching Algorithm）对兴趣点进行索引；然后，依据“椭圆上的点到两焦点的距离之和小于椭圆外的点到两焦点的距离之和”的性质，设计了ESRA（Elliptic Search Refinement Algorithm）算法将空间数据集的搜索区域剪枝细化；最后，提出BestTD（Best Time Dynamic）算 法来解决 TDGTP问题.

综上所述，本文主要贡献如下：

（1）正式定义并研究了时间感知的动态组旅行规划查询（TDGTP）问题；

（2）设计了一种有效的综合索引结构，称为TIR-Tree，提出了基于时间和关键词的剪枝来高效、快速地查找相应的兴趣点；

（3）对于大规模的兴趣点集，开发了一种基于椭圆区域的剪枝，利用椭圆性质，设计了ESRA（Elliptic Search Refinement Algorithm）算法来对空间数据集剪枝，从而减少检索数据集的数量.

2 相关工作

文献［1］讨论了空间数据库中的一种新型行程规划查询（TPQ），研究了度量空间中TPQ 的快速近似算法.文献［2］首次引入团体旅行计划（GTP）查询的概念并针对Euclidean 空间做了介绍，将kGTP 定义为：如果一个组查询一个GTP 的k组数据点，则该查询称为k 组旅行计划（kGTP）查询.文献［3］将POI搜索区域细化为椭圆区域，计算组中每个成员形成的椭圆区域，其中每个椭圆的焦点位于相应成员的源位置和目标位置上.文献［4］研究了道路网络中的组最优排序路线（GOSR）查询问题，指出在Euclidean 空间中提出的GTP 算法会产生非常高的查询处理开销，且不能扩展到道路网中.

文献［5］为克服固定团队规模的限制，提出了NaiveDGTP算法和FastDGTP算法来处理DGTPQ，但这两种方法在道路网上并不适用.文献［6］提出了DGTP 算法和M-DGTP 算法来解决道路网上的小组规划问题，相比之下，M-DGTP 算法处理的时间较快，内存开销较小，但该算法需要依次访问道路网上的兴趣点，处理的数据对象多且时间长.文献［7-8］研究了空间数据库中的序列团体旅行计划查询（SGTPQ）问题，对于不同的团体规模和查询区域，所提出的PGNE算法响应时间较短，内存开销较少.

文献［9］提出了基于方向感知的空间关键词搜索，它以空间点、方向和一组关键词为参数，找到查询的k 个最近邻居，每个邻居都位于搜索方向上且包含所有查询关键词.文献［10］提出了时间感知布尔空间关键词查询（TABSKQ），设计了一种高效的混合索引结构TA-tree 及相关算法来处理TABSKQ.文献［11］提出了道路网络上的时间感知空间关键词查询（TSK）问题，设计了一种高效索引结构TG 及基于TG 索引的有效算法.文献［12］提出了时间感知空间关键词覆盖查询（TSKCQ），设计了PQA 算法去评估成员在时间和空间上的满意度，并返回具有最佳成本函数的对象值.

文献［13］首次探讨了在查询位置与空间对象之间的距离最短路径道路网络上处理top-k 空间关键词查询问题.文献［14］研究了最接近关键词搜索的最佳覆盖，提出的keyword-NNE 算法能减少生成的候选关键词覆盖数量.文献［15］引入了一种新颖的空间关键词覆盖（SK-COVER）问题，建立了一个O（log m）近似算法，设计了有效的访问策略和修剪规则，以提高整体效率和可扩展性.

3 问题描述

3.1 兴趣点

假设在数据空间有一组时空文本对象o∈O，每个对象 o 定义为（id，doc，t），其中 o.id 是对象 o 的唯一标识，o.doc是一组用来描述对象o的关键词集合，其形式为 o.doc=｛（o.key1），（o.key2），…，（o.keyi）｝，o.t表示对象o的有效时间，形式为（st，et）其中st和et分别为对象o的起始时间和结束时间.其中，将o.t进行整数化，以一个小时为单位.例如，购物中心的有效时间是（09：00-12：00），（09：00-12：00）中的任何时间戳都可以转化为单位时间（9，12）.表1 列出的是本文中出现的符号及其定义.表2是对象信息.

表1 符号与定义Tab.1 Symbols and definitions

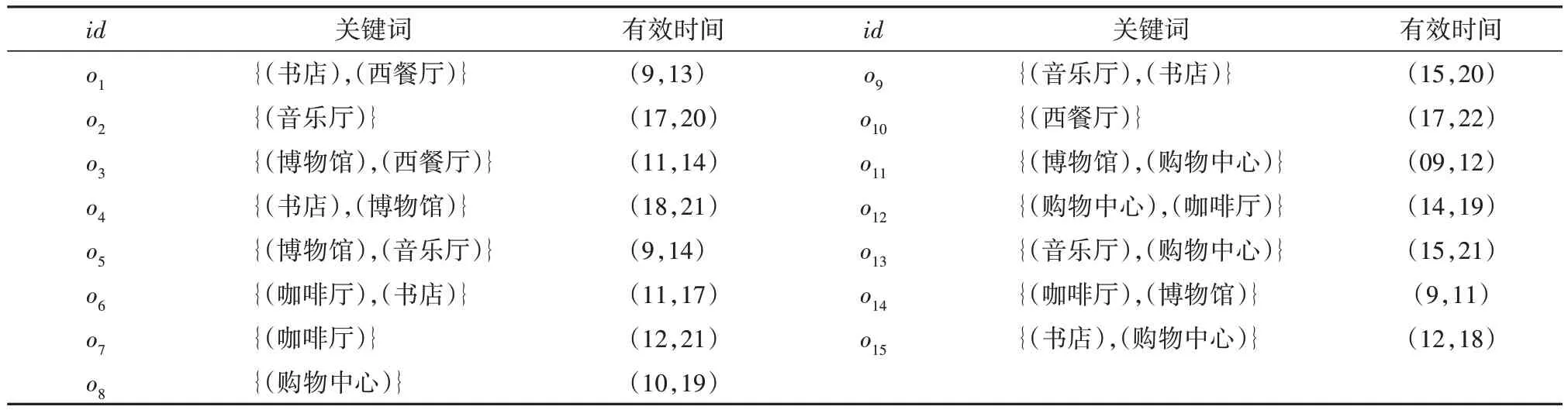
表2 对象信息Tab.2 Object information

3.2 时间感知的动态组旅行规划查询

已知数据集O和一个时间感知的动态组旅行规划（TDGTP）查询q=（U，S，D，P，T），其中U=｛u1，u2，…，un｝表示小组成员集合，S=｛s1，s2，…，sn｝是每个成员ui的起始位置集合，D=｛d1，d2，…，dn｝是目标位置集合.P 是一组关键词集合，表示成员查询目的.T 是成员指定的任意查询时间区间如（9，12）.查询q 返回一条各个成员从S 出发、到D 结束且符合q.P 和q.T约束条件的最佳路径.

接下来是搜索区域边界的计算.椭圆焦点的公式如下：

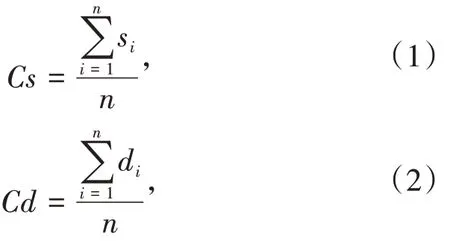
其中 si是成员 ui的起点，di是成员 ui的终点，n 为组成员数量.

椭圆主轴范围为：

其中n 是小组成员数量，总行程距离是所有成员的行程距离之和.

4 索引结构TIR-Tree

R-tree 是目前最流行的空间索引结构之一，它运用了空间分割理念，用作空间数据存储的树状数据结构.倒排索引是实现“单词-文档矩阵”的一种具体存储形式，是常用的文本索引结构之一，通过倒排索引，可以根据单词快速获取包含这个单词的文档列表.传统的空间查询和关键词搜索使用不同的索引技术和查询算法耗时又费力，为有效地处理TDGTP 问题，本文将R-tree 上的每个非叶子结点关联上两个倒排文件，在查询包含空间文本信息的文件时拥有较高的效率，这种混合数据结构被称为TIR-Tree索引.

在二维空间中，对于不规则几何图形通常采用最小边界矩形MBR 来构建索引.本文采用MBR 的方法，从叶子结点开始用MBR 将空间框起来，结点越往上，框住的空间就越大，从而实现对空间的分割，如图2所示：首先假设所有数据对象的位置都是二维空间下的点，图中标识了R6区域中的数据，将它看作是多个数据围成的一个区域，为了实现R树，用一个MBR 框住形成区域R6.采用同样的方法，一共得到了4 个最基本的MBR，这些MBR 被存储在非叶子结点中.下一步是进行高一层的处理，此时的R3和R4这两个矩形距离最为靠近，因此可用一个更大的矩形R1恰好框住这两个矩形，同样，R5和R6恰好被R2框住.所有最基本的MBR被框入更大的矩形中后，再次迭代，用更大的框框住这些矩形.

图2 TIR-Tree的划分Fig.2 Division of TIR-Tree

TIR-Tree 整体结构如图 3 所示 .TIR-Tree 以 R 树的形式构建，从空树开始，不断插入划分的MBR，直到生成一棵完整的R 树.每个非叶子结点用四元组（ra，rectangle，ra.di，ra.ti）表示，其中 ra 存储的是子节点地址，rectangle 是覆盖所有子结点的MBR 的最小矩形，ra.di 是关键词描述标识符，连接关键词倒排文件列表，其中第一列为关键词信息，第二列为包含对应关键词信息的子结点的MBR.ra.ti 是有效时间信息的标识符，连接有效时间的倒排文件，其中第一列为有效时间信息，第二列为包含对应时间信息的MBR.每个叶子结点包含许多形式为（o，o.rec，o.di，o.ti）的条目，其中o是数据空间的对象，o.rec是对象o 的边界矩形，o.di 是对象o 的关键词标识符，o.ti是对象o有效时间的标识符.

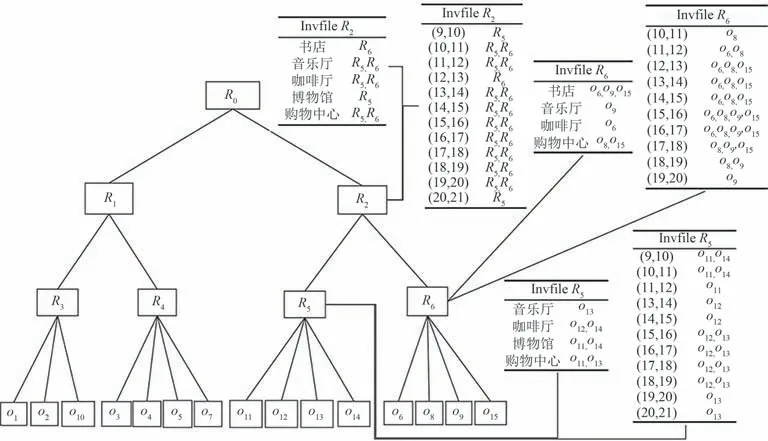
图3 TIR-Tree综合索引结构Fig.3 TIR-Tree comprehensive index structure

5 查询处理算法

这里首先提出基于TIR-Tree 的剪枝策略，然后介绍ESRA细化搜索空间算法和解决TDGTP查询处理的BestTD算法.

5.1 基于TIR-Tree的剪枝策略

5.1.1 基于TIR-Tree的剪枝

引理1 已知一个TDGTP 查询q=（U，S，D，P，T）和一个区域Ei，如果q.P ∩ Ei.P=Ø，则区域Ei可以被安全地削减.

证明 已知查询的关键词集合为q.P，区域Ei内所有对象关键词的并集为Ei.P.若q.P 与Ei的交集不为空，表示区域Ei内有满足查询关键词要求的对象；反之，区域Ei内的对象都不满足要求，可以被剪枝.

引理2 已知一个TDGTP 查询q =（U，S，D，P，T）和一个区域Ei，如果q.T ∩ Ei.T= Ø，则区域Ei可以被安全地削减.

证明 已知查询q 的时间信息为q.T，区域Ei内所有对象营业时间的最大区间为Ei.T.若q.T 与Ei.T的交集不为空，表示区域Ei内有满足查询时间要求的对象；反之，区域Ei内的对象的营业时间都在查询给定的时间之外，可以被剪枝.

5.1.2 基于TIR-Tree的剪枝算法KMA

基于TIR-Tree 的剪枝算法KMA 具体流程见算法 1，初始化队列 Qinit、集合 Ponec和指针 TNode，其中Qinit用来存放候选结点，Ponec用来保存所有符合约束的兴趣点集合（第1行）.将TIR-tree的根结点放入队列Qinit（第2 行）.当队列Qinit不为空，则从根结点自上而下地进行处理，遍历根结点的子结点.首先TNode指向队列Qinit的头元素，判断TNode是否满足查询关键词和时间约束；若满足，继续判断TNode是否为非叶子结点，若是，则将该结点的子结点存入队列Qinit，否则将该结点存入集合Ponec（第2-9 行）.遍历完成后，返回集合Ponec（第10行）.

images/BZ_114_1284_1524_2243_1581.png输入：一个TDGTP查询q=（U，S，D，P，T），关于数据集O的TIR-Tree输出：满足空间关键词要求的兴趣点集Ponec 1 Ponec=Ø；Qinit=Ø；TNode=Ø 2 将TIR-Tree树的根结点R0放入队列Qinit 3 while Qini≠tØ do 4 TNode=Qinit.pop（）5 if TNode的关键词∩q.P and TNode的时间∩q.T then 6 if TNode是非叶子结点then 7 Qinit.Push（TNode.children）8 else 9 Ponec ←TNode 10 Return Ponec

5.2 基于搜索区域的剪枝

5.2.1 搜索空间的剪枝

已知一个TDGTP 查询q=（U，S，D，P，T）和一个数据集搜索空间，将搜索空间从整个搜索区域减小到TDGTP 查询区域.为了计算搜索区域的边界，需计算一组椭圆区域集.首先根据公式（1）、（2）计算初始成员（此时尚未加入的成员）的起始位置和目标位置的质心，即椭圆焦点，主轴为Tdist，形成E1椭圆；然后分别计算在某个兴趣点新加入成员的起始位置和目标位置的质心，形成Ei椭圆；最后区域为所有椭圆的交集，见图4.

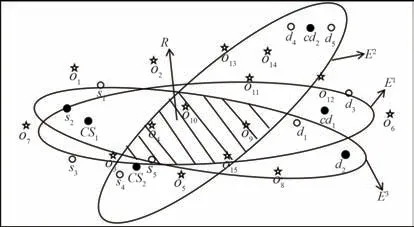
图4 搜索区域的细化Fig.4 The refinement of search area

图 4 中，U =｛u1，u2，u3，u4，u5｝，小组成员的起始位置为 S=｛s1，s2，s3，s4，s5｝，目标位置为 D=｛d1，d2，d3，d4，d5｝.u1和 u3是初始成员，u4和 u5是在第 1 个兴趣点加入的成员，u2是在第2 个兴趣点加入的成员.第11 个椭圆区域E1；然后计算第2 个椭圆焦点Cs2=计算第3 个椭圆焦点，因为第3 轮加入的成员只有u2，所以第3个椭圆的焦点就是s2和d2，形成第3个椭圆区域E3.R是3个椭圆E1，E2，E3的交集区域.

5.2.2 搜索区域ESRA算法

椭圆剪枝算法见算法2.两个队列Scand，Dcand以及3个集合cvs，cvd，Cur初始化为空，集合Ptwoc初始为O.其中，Scand用来存放成员起点，Dcand用来存放成员目标点，Ptwoc用来存放椭圆交集内的兴趣点，cvs 和cvd分别保存计算的椭圆焦点（第1 行）.将每轮加入行程的成员起点和终点存入Scand，Dcand（第2行）.当两个队列不为空时，根据公式（1）、（2）计算每一轮次的几何质点，分别存放在cvs 和cvd 中，然后使用FindElliptic 函数形成椭圆区域，并将该区域内的兴趣点存入Cur，Ptwoc存放所有椭圆交集区域的兴趣点（第3-9行）；最后返回集合Ponec（第10行）.

images/BZ_115_242_2303_1201_2360.png输入：S=｛s1，s2，…，si｝，D=｛d1，d2，…，di｝，O=｛o1，o2，…，oi｝输出：输出细化区域范围的兴趣点集Ptwoc 1 Ptwoc =O ；cvs=Ø ；cvd=Ø ；Scand=Ø ；Dcand=Ø ；Cur=Ø 2 将S、D按照加入行程的顺序排列分别存入Scand，Dcand 3 while Scand ≠Ø and Dcand ≠Ø do 4 Cens=Scand.pop（）5 Cend=Dcand.pop（）6 cvs←按照公式（1）计算Cs 7 cvd←按照公式（2）计算Cd 8 Cur ←将 FindElliptic（cvs，cvd，Tdist）内的兴趣点9 Ptwoc=Ptwoc ∩Cur 10 Return Ptwoc

5.3 基于时间感知的动态组旅行规划BestTD算法

前两小节讨论的基本算法分别返回满足约束条件的兴趣点集，在此基础上，将兴趣点按照关键词排序，得到所有的候选路径，然后对候选路径序列进行遍历，根据公式（4）、（5）计算候选路径的距离，从而获得总行程距离最小的最优路径.

查询算法见算法3.首先初始化3 个集合PT，LTcand和 LT 及一个队列 PTcand，Lmin被初始化为∞，（PT用来存放算法1 和算法2 剪枝后的兴趣点，PTcand用来存放排列后的候选路径，LTcand用来保存队列PTcand出队元素，LT 存放筛选后的最优路径）（第1行）.调用KMA 算法和ESRA 算法，将返回的集合交集存放在PT，并将PT 中的兴趣点按照关键词排列的候选路径存入 PTcand（第 2-3 行）.当 PTcand不为空时，遍历每条候选路径，根据公式（4）和（5）计算出每条候选路径的总行程距离TD，将TD 与Lmin比较，若TD 小于Lmin，此时的候选路径存入LT，最小总距离行程的值赋值给Lmin（第4-12 行）.最后返回路径LT（第13行）.

images/BZ_115_1284_1478_2243_1535.png输入：一个TDGTP查询q=（U，S，D，P，T），关于数据集O的TIRTree，O=｛o1，o2，…，oi｝输出：最优路径LT 1 PT = Ø；PTcand = Ø；LT= Ø；Lmin= ∞；LTcand= Ø 2 PT←KMA（q，O）∩ ESRA（S，D，O）3 将PT中的兴趣点o按照q.P的顺序排列并插入PTcand 4 while PTcand ≠Ø do 5 LTcand =PTcand.pop（）6 n←|U|7 按照公式（4）计算PD 8 按照公式（5）计算TD 9 if TD ＜Lmin then 10 LT=LTcand 11 Lmin=TD 12 end if 13 查询结束，返回LT

算法复杂度分析：根据算法1，在整个搜索空间内，假设关键词的总和为Nk，查询关键词数量为|q.P|，每个兴趣点平均分配Ki个关键词，此时获得满足2 是返回椭圆交集区域内的兴趣点，此时满足关键算法2 的基础上，算法3 检索到在椭圆交集区域内满足关键词和时间约束条件的兴趣点，综上所述，令空间对象总数为|O|，则满足条件的对象总数为

算法3 中，若不采用剪枝策略，此时执行次数m为|O|，则算法3 的最坏时间复杂度为O（|O|）；当剪枝|O|，while 内的语句会随着问题规模m 的增加呈线性

6 实验案例

6.1 实验设置

本文以路网数据集的结点位置作为兴趣点对象位置，使用2 个真实的路网数据集——美国California和德国Oldenburg真实路网数据在Euclidean空间评估算法，如表3所示.CA 路网有21048个结点和21693 条边.使用Zipfian 分布为每个对象分配2-3 个关键词，每个关键词中的平均、最大和最小对象数分别为 319、3024 和 123.OL 路网包含 6105 个结点和7305条边，使用Zipfian 分布为每个对象分配2-3 个关键词，每个关键词中的平均、最大和最小对象数分别为103、887 和33.

表3 实验数据集Tab.3 Experiment datasets

本实验将其数据空间归化成一个1000×1000平方单位面积，使用TIR-Tree结构来索引数据对象.对3 个参数（如表4 所示）进行设置：成员数量n、查询关键词个数m 以及椭圆长轴的大小Tdist.本次实验设备为Intel Core i5-5200U，2.20 GHz CPU，8.00 GB RAM Windows 10 的计算机，所有算法在Java 1.8.0_191的运行环境下完成.

表4 参数设置Tab.4 Parameters setting

6.2 实验结果

本节将展示 BestTD 算法与 TABASSUM 等人［5］提出的NaiveDGTP 算法处理TDGTP 查询的性能比较分析.

（1）数据集的影响.图5（a）和5（b）分别显示了两种算法在CA 和OL 数据集下处理时间和内存开销.实验结果表明：不管是查询时间还是内存开销，BestTD 算法都要优于NaiveDGTP 算法.这是因为NaiveDGTP 基于动态规划，随着数据结点的增加，最短路径和部分行程的计算量也在增加.

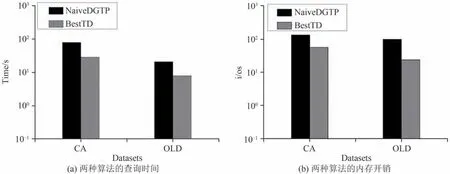
图5 两种算法在不同数据集下的性能Fig.5 Performance of the two algorithms in different datasets

（2）查询关键词m的影响.实验结果表明（图6），两种算法的查询处理时间均随查询关键词数量的增加而增加，但BestTD 算法的查询处理时间远小于NaiveDGTP 算法.这是因为随着查询关键词个数的增加，查询的搜索范围变大，查询处理对象的数量增加.但BestTD 算法相较于NaiveDGTP 算法效率要高，它能够根据查询关键词更快地查询到满足条件的对象.因此，从图6 可以看出，在查询关键词数量的影响下，BestTD 算法查询性能优于NaiveDGTP算法.

图6 查询关键词的影响Fig.6 Impact of query keywords

（3）组大小n 的影响.图7 显示了组大小对两种方法的影响，正如预想的那样，BestTD和NavieDGTP两种算法的查询时间都随着组大小的增加而增加.因为组大小的增加将导致更大量的路径计算，从而导致处理时间变长.从结果中观察到，BestTD 所需要的处理时间要比NavieDGTP少得多.

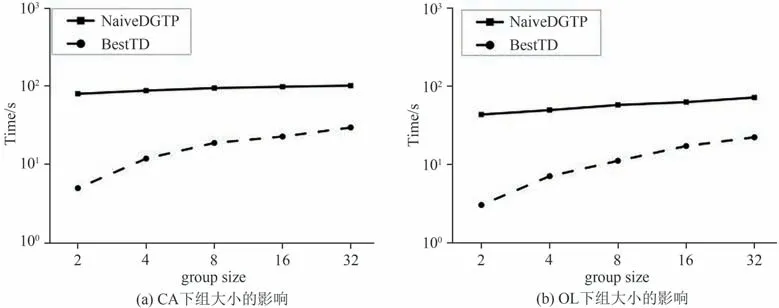
图7 组大小的影响Fig.7 Impact of group size

（4）椭圆主轴大小Tdist的影响.图8显示了随着椭圆主轴大小的增大，两种方法的处理时间都有所增加.这是因为椭圆主轴越大，搜索区域越大，查询的数据集越多，从而处理的时间越长.实验中观察到 ，BestTD 算 法 要 优 于 NaiveDGTP 算 法 . 对 于NaiveDGTP 算法来说，它没有任何修剪策略来减小搜索空间，而是使用整个数据空间来计算最佳团体旅行，导致处理时间长；而BestTD 算法采用了椭圆属性细化搜索空间，所以其查询处理时间要远远低于NaiveDGTP算法.

图8 椭圆主轴大小的影响Fig.8 Impact of ellipse major axis

7 结语

本文研究了基于时间感知的动态组旅行规划查询问题（TDGTP）.为快速定位到组成员需求的兴趣点，构建了一个综合索引结构TIR-Tree 并提出相关的关键词查询KMA 算法.此外，提出了一种基于椭圆剪枝方法（ESRA），细化搜索空间为椭圆交集区域.提出一种基于KMA 和ESRA 的查询处理算法BestTD 来分析评估 TDGTP 问题 .通过对 BestTD 与NaiveDGTP 算法在真实路网合成的数据集上进行对比，证明本文所提方法是高效可行的.