基于多层感知器的端到端车道线检测算法

王月鑫，伍鹏, ，周沛，叶旭，周顺平

（1 长江大学 电子信息学院，荆州 434023；2 中国地质大学（武汉）工程学院，武汉 430074；3 中国地质大学（武汉）国家地理信息系统工程技术研究中心，武汉 430074）

近年来，随着计算机视觉和人工智能的快速发展，传统的汽车行业与这些先进的技术结合得越来越紧密，车道线检测技术广泛应用于车道偏离预警［1］、自适应巡航控制［2-3］、交通理解［4］等领域中 .此外自动驾驶技术也受到了大量关注，能否准确高效地识别出车道线是实现高级别自动驾驶的关键一步.所以高效准确的车道线检测技术具有重要的工程应用价值.

生活中常见的车道线是一种细长的管状结构，具有较强的形状特性［5］，传统的车道线检测方法通常先手工操作提取特征［6-7］，再通过 Hough 变换［8-9］、随机采样一致性［10-12］等后处理来拟合线形车道，这种检测模型鲁棒性差，无法适应不同环境下的车道线检测.目前对于车道线检测的研究主要集中于基于深度学习的检测算法，有四种主流方案，即图像分割方案［4，13-15］，逐行分类方案［16-17］，多项式拟合方案［5，18］和基于锚的方案［19-20］.

图像语义分割被广泛应用于街景识别、目标检测中［21］，将车道线检测看成一个图像分割问题，如SCNN［4］利用图像分割模型分割出车道线，使用消息传递，以及额外的场景注释来捕获全局上下文信息提高准确率，具有比传统图像处理方法更强的语义表示能力，但密集的像素级通信，需要大量的计算资源，导致算法的处理效率低；基于逐行分类的方案是将车道线看成一系列的行锚，如文献［17］在处理过程中对道路图像每行检测出一个像素属于车道线，相较于图像分割算法，减少了计算量，提高了推理速度，但此方法的泛用性较低，无法适应多环境下的车道线检测；基于多项式拟合的方案，是将车道线看成曲线，直接对参数进行学习，每条车道线输出一个多项式，如LSTR［5］将每条车道线视为一个三次曲线，利用TransFormer［22］强大的编码和解码能力，拟合出每条车道线对应的参数，在推理速度上有所提升，但准确率并没有优于其他方法；基于锚的方案，如LaneATT［20］将每条车道线都表示为一条直线的锚和锚的横向偏移.与逐行分类方案类似，这种方法利用了一定的先验知识，即车道线通常是直的，然而固定锚的形状导致描述线性形状的自由度很低，因此对于弯曲路况的预测结果较差.

此外在光线变化、雾天雨天、车辆行人遮挡等复杂环境下完成车道线检测，不仅需要考虑车道线的局部信息，更需要对车道线进行更高层次的语义分析，进行全局结构信息提取.近期，许多对多层感知器［23-26］（Multi Layer Perceptron，简称MLP）的研究表明，MLP 能够较好的提取图像的全局语义信息，但在局部语义信息的提取上没有达到好的效果，且文献CycleMLP［23］在图像分割等计算机视觉的下游任务中获得了很好的效果，而文献［24，27-28］中通过结构重参数化技术实现训练与推理的解耦，在不牺牲推理速度的情况下换来了不错的精度提升，如Rep-MLP［24］模型，训练时在其内部构建组卷积层获取局部信息，将重参数化技术与MLP 结合，此方法在模式识别中获得了较好的效果.

在借鉴已有的车道线检测方法的基础上，结合车道线的全局结构特征和局部语义信息，提出了一种简单高效的基于多层感知器的车道线检测方法，该方法能快速、准确地检测出车道线.本文的创新点在于以下3点：

（1）提出了一种新的基于MLP 的车道线检测算法LaneMLP，将MLP 与重参数化技术应用于车道线检测，提高了端到端的车道线检测效率.

（2）提出了一种新的逐行分类的长线型检测模型，此模型在在预处理阶段降低了计算量提高模型的推理速度，为实际运用提供了更高的可行性.

（3）本文模型在检测速度和准确率上都有较大提升，使用本文模型在CULane 数据集上进行测试，实验结果表明：在推理速度超过每秒350 帧的情况下，检测准确率达到了76.8%，与目前已提出的方案相比具有很强的竞争力.

1 基于MLP的车道线检测模型

给定一张待检测图片 I ∈ RC×H×W，其中 C，H，W分别表示图像的通道数，高度和宽度；目标是检测出所有构成车道线的点集：

其中：N 表示待检测图片中的车道线数目，k 表示图像中每条车道线的最大采样数，将检测到的点显示在图像上，实现端到端的车道线检测.

LaneMLP 算法模型主要由两部分组成，分别为全局感知器和局部感知器，如图1所示.全局感知器（具体介绍见1.2 节）主要由具有残差连接的MLP 模块组成，该模块的输入为图像I 经过逐行分类模型（具体介绍见1.1 节）预处理后得到图像 I′ ∈ RY×X，其中Y，X 分别表示预处理后图像高和宽的栅格数量；局部感知器（具体介绍见1.3）主要由分组卷积模块gConv 构成，该模块有四个并行的二维卷积，对输入图像I 进行局部信息提取.最后将特征数据通过线性分类层实现栅格的分类，整个模型的输出为构成车道线所有点的集合.需要注意的是在模型训练阶段线性分类层的输入为全局感知器和局部感知器的特征张量的叠加，在模型推理阶段线性分类层的输入为全局感知器的特征张量.训练过程的具体计算如式（2）和式（3）：

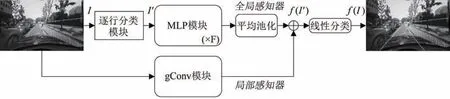
图1 LaneMLP结构模型Fig.1 Model of the LaneMLP algorithm

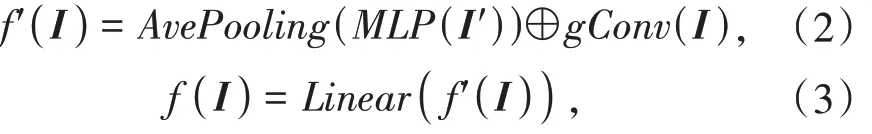
其中MLP 表示对图像进行多层感知器处理，gConv表示组卷积操作，AvePooling 表示平均池化，⊕表示特征张量的叠加，Linear表示线性层.

推理过程中无需组卷积操作，故推理过程中需将式（2）转换为式（4），最后经线性分类输出.

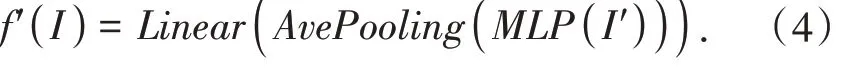
1.1 逐行分类模型

文献［17］中的逐行分类模型UFASTResNet 是以锚点的形式对每一帧图像的固定锚点进行分类，判断是否属于车道线，同时在模型的右侧引入了一列背景锚点来表示这一行是否存在车道线，这种框架式模型对图像的结构信息有较好的表达能力，但忽略了图像的局部语义信息，使其在复杂环境中检测效果差.因此提出一种新的逐行分类模型，如图2所示，将输入图像分成Y×X个栅格，Y=H h，X=W w其中h，w 分别表示每个栅格的高和宽.对于车道线在垂直方向上存在的范围，可以引入参数V来表示，通过一个线性层［29］训练参数.

图2 逐行分类模型Fig.2 Model of the row-wise classification

通过这种新的逐行分类模型，车道线检测任务可以看成一个V 行的分类任务，每行进行X 个类别为N + 1的分类操作，判断V × X 个栅格是否属于车道线以及属于第几条车道线，与逐像素的分割模型相比，该模 型 的计算量由 H × W 降为 V × X，而V ≪ H，X ≪ W.以 CULane 数据集［4］为例，在数据规模设置相同的情况下，SCNN 模型的计算量为2.8 × 106，本文模型的计算量约为 2.8 × 104，可见在预处理阶段降低了模型的计算量.

该模型既保留了UFASTResNet 模型提取全局的结构信息的优势，又可以与MLP 模块和分组卷积模块结合，增强模型提取局部语义信息的能力，从而提高复杂环境下的车道线检测.

1.2 全局感知器

全局感知器的算法模型如图3 所示，该模型首先对预处理后的图像I′进行栅格编码操作，以V × X个不重叠的栅格作为输入，其中每个栅格的大小为h × w，在构建模型时默认值设置为h = w = 10.栅格通过一次二维卷积操作，二维卷积的输入维度为Rhw×VX×C输出维度为 RV×X×l，卷积核大小为 h × w，水平步长为w，垂直步长为h，即对每个栅格提取一个长度为l 的特征编码（Token），再沿X 方向将特征张量压平得到 M ∈ RVX×l，之后 M 通过 F 个 MLP 模块，其中MLP 模块由两个连续子层组成，如图4所示.

图3 全局感知器算法模型Fig.3 Model of the global perceptron

图4 MLP算法流程Fig.4 Flow chart of the MLP block

对于两个子层，分别为在跨栅格操作的线性层（Cross-grid 层）和在跨通道操作的前馈层（Cross-channel 层），图4 中，每个子层间都有一个残差连接［30］，且通常在进入每个子层前都会先经过标准化处理，如层标准化（Layer Normalization），本文采用仿射变换［26］替换标准化处理，此操作对每个子块的输入和输出进行缩放和移动，定义为：Affine(x) =Diag(α)x + β，其中α，β 为可训练的参数，训练中初始化为α = 1，β = 0，在使用仿射操作时，将独立的应用于输入数据的每一列，与标准化处理不同，该仿射变换不依赖于任何批处理信息，可以使训练更稳定.

激活函数GeLU［31］，在非线性变换中引入随机正则化，提高模型的泛化能力，定义如式（5）：

其中Φ(x)为正态分布的概率函数，可以采用正态分布 N(0，1)，也可以采用一般正态分布 N(μ，σ)，将μ，σ 视为可训练参数，当输入为标准正态分布时可简化为：

总体而言，对于MLP 模块中的子层有如下转换关系：

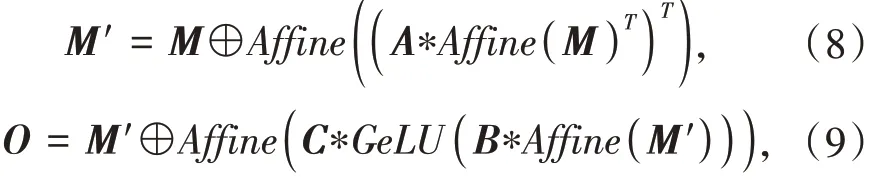
其中A，B，C 为该子层中的主要可训练权重，*为矩阵相乘，Affine(·)为仿射变换，(·)T为矩阵转置.

1.3 局部感知器

局部感知器模块如图5 所示，先由4 个不同的并行卷积构成一个卷积组［24］，再在每个卷积层处理后连接一个批标准化［27-28］，输入为原始图像I，输出为4 个特征张量的和.对于卷积核的大小需要满足k ＜ min{h，w}，取4组卷积核，分别为1 × 1，3 × 3，5 ×5，7 × 7，为保持卷积处理后得到的特征图具有相同的分辨率，分别设置4个填充参数padding = 0，1，2，3.该模块通过不同的感受野提取输入图像的局部语义信息，作为训练阶段的辅助信息帮助训练，从而获得更好的参数.

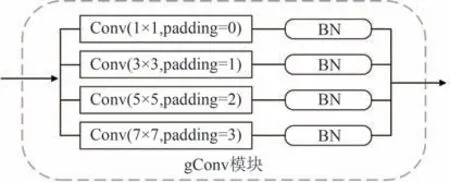
图5 局部感知器算法模型Fig.5 Model of the local perceptron

需要注意的是，局部感知器仅仅在训练过程中使用，推理时只使用全局感知器进行预测，因此加入局部感知器不影响模型的推理速度，这是本文模型推理速度快的一个重要原因.

1.4 损失函数

对于车道线被遮挡部分，很难利用局部的语义信息进行车道线的检测，考虑车道是一种细长的条形线，相邻的车道线保持相似的曲率，因此可以利用全局的结构信息来尽可能的恢复被遮挡的车道线［17］，通过结构损失函数进行约束车道线的全局结构信息，其定义如下：

首先在车道图像输入后需要对栅格进行分类操作，分类损失函数定义为式（10）：

其中 Ti，j，Pi，j分别表示第 i 条车道线在第 j 行的独热码标签和预测概率，Pi，j的维度为X.

其次考虑在一条车道线中构成车道线的点之间是连续的，计算所有相邻预测点的L1范数和，抑制预测结果的分散，使检测的车道线更加平滑，其相似度损失函数定义为式（11）：

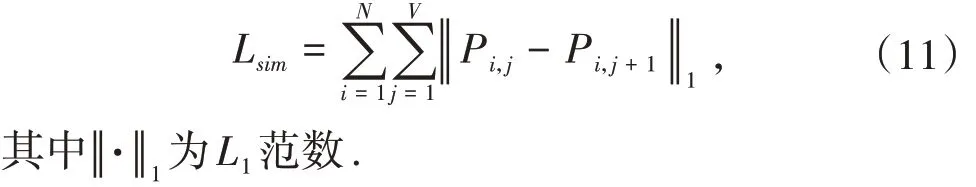
根据实际的车道线分析，大多数车道线都是直线，故使用二阶差分方程来进一步约束车道线的形状，实现语义上的车道线检测，如被遮挡部分，其形状损失函数定义为式（12）：

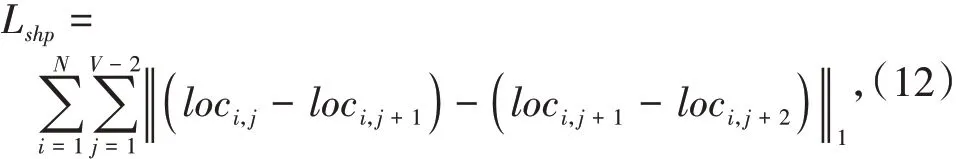
最后垂直车道线范围是通过逐行预测车道线是否通过当前行来确定的.使用Softmax 损失函数（Softmax+交叉熵损失函数），如式（13）：

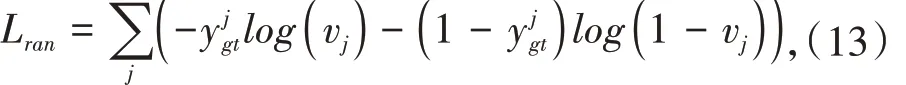
其中vj表示第j 行存在车道线的概率，yjgt为第j 行是否存在车道线的标签.

综上所述，本文所使用的损失函数定义为：

其中λ，μ，γ 为损失系数，训练中分别初始化为λ =0.6，μ = 0.2，γ = 0.2.

2 实验结果与分析

2.1 实验配置

2.1.1 实验数据集与设备

为验证本文所提出的方法，分别在TuSimple［32］和CULane 两个数据集上进行实验验证.TuSimple 是一个广泛使用的高速公路驾驶场景数据集，其场景较为简单.CULane 数据集环境较复杂，有9 个不同的场景.两个数据集的详细信息如表1所示.实验中使用Python 3.7 作为开发语言，使用PaddlePaddle 2.1.2 作为深度学习框架.硬件配置为：4 核Intel（R）Xeon（R）Gold 6271C CPU @ 2.60GHz、32GB RAM、显卡Telsa V100×4，显存32GB.

表1 实验数据集Tab.1 Datasets of experiments

关于实验数据集的车道线标注如图6 所示，其中第一行为Tusimple 数据集，其余均为CULane 数据集.

图6 数据原图与标注Fig.6 Original datasets with annotation

2.1.2 算法评价标准

对于Tusimple数据集，使用官方［32］的评价指标，准确率计算公式如式（15）：

其中，Npred是预测车道点的数量，Ngt是标记车道点的数量，如果预测的点与标签的距离在20个像素点以内即认为预测结果正确.

对于CULane 数据集，采用SCNN 所使用的评价指标，将车道标记视为一条宽度为30 像素的线，取预测车道线与标签之间的交并比（IoU），对于IoU 大于0.5的被认为是正确的预测，其F1-measure计算如式（16）：

示真阳性率即被正确预测的车道点的数量，同理FP表示假阳性率，FN表示假阴性率.

2.1.3 实验的详细参数配置

训练图像尺寸为560 × 1000，原始数据通过随机缩放、旋转、颜色抖动和水平翻转进行数据增强.使用的优化器为AdamW，权重衰减率设置为0.01，使用余弦衰减学习率，在前30 轮中，学习率从4 ×10-4增加到4 × 10-3，在剩余的轮次中学习率衰减至4 × 10-5，λ，μ，γ 为损失系数分别设为 0.6，0.2，0.2，批大小设置为64，对于TuSimple数据集训练200轮，CULane 数据集训练300 轮，除消融实验外，参数设置在所有实验中都相同.

2.2 消融实验

2.2.1 全局感知器的层数与栅格编码长度

在研究全局感知器对空间特征的影响过程中，设置栅格编码长度为28，使用不同数量的感知机层比较测试的准确率.实验结果如图7所示，从图中可以看出，当MLP模块的层数小于16时测试的准确率随层数增加而提高，当大于16 层时，准确率因过拟合而降低.因此本文中的模型将MLP 的层数设置为16.

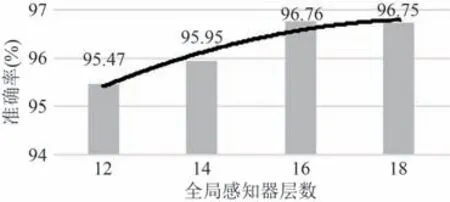
图7 全局感知器层数对准确率的影响Fig.7 Effects of glocal percetron layers

为了研究栅格编码长度对车道线结构特征以及模型推理效率的影响，设置全局感知器层数为16，对多个编码长度分别实验，验证其准确率，其结果如图8 所示，从图中可知栅格编码长度小于28时，准确率随编码长度增加稳步提高，编码长度为大于28时准确率基本保持稳定，可见此时模型表达力已达最优，故栅格编码长度为28.

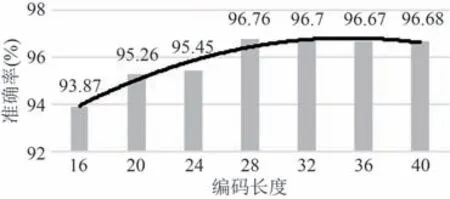
图8 栅格编码长度对准确率影响Fig.8 Effects of griding embeding lengths

2.2.2 局部感知器有效性验证

在验证局部感知器的有效性的实验中，对训练与推理阶段是否使用局部感知器分别设置三组对照实验，算法组合与实验结果如表2所示，由结果可知在训练阶段加入gConv 模块，推理结果的准确率提高至96.76%，与不加gConv模块相比，准确率提高2.38%；而在推理阶段加入gConv 模块推理速度大幅降低，推理准确率没有提升，由此可见对模型进行重参数化设计可以兼顾推理速度和准准确率.需要注意的是为了与其他模型比较，推理速度的实验结果在GPU为1080Ti的设备上计算得到.

表2 局部感知器对性能的影响Tab.2 Effects of local perceptron

2.2.3 各模型速度与准确率的对比

在Tusimple 数据集中，选用5 个模型（Res18-Seg［33］，SCNN［4］，PloyLaneNet［18］，FASTResNet18［17］，LSTR［5］）推理速度的统计量为每秒可处理图像的帧数（FPS），根据文献［17-18］的相关说明所选用的对比模型的推理速度均在GPU 为1080Ti 的设备上处理得到，与本文模型测试推理速度的设备规格相同.实验结果如表3 所示，结果显示本文模型在准确率优于其他五种模型的同时，推理速度也具有很强的竞争力.

表3 各模型的准确率和推理速度Tab.3 Accuracy and speed of each model

2.3 泛化性实验

为研究本文模型的泛化能力，在更宽泛的数据集CULane 上进行训练预测，分别使用8 个模型（SCNN［4］，ERFNet-E2E［34］，FastDraw［16］，SAD［35］，UFASTResNet34［17］，UFASTResNet18［17］，ER-FNet-IntRA-KD［36］，CurveLanesNAS-S［37］）在 CULane 数 据集上的实验结果与本文模型的实验结果对比，各模型的准确率和推理速度的实验结果如表4 所示，其中（-）表示数据不可用，准确率分为整体（Total）准确率和其余9 个不同场景（Normal，Crowded，Dazzle，shadow，No-line，Arrow，Curve，Cross，Night）的子类准确率，场景类别为十字路口（即Cross）时评测指标为假阳性率FN，数值越小越好，其余类的评测指标为F1-measure，从表中的数据可知，本文模型虽然在拥挤、曲线等环境中的效果较差，但在普通、炫光、阴影、夜间和十字路口等场景中效果更好，整体的检测准确率相较于其他模型达到了最优，且获得了最快的推理速度.

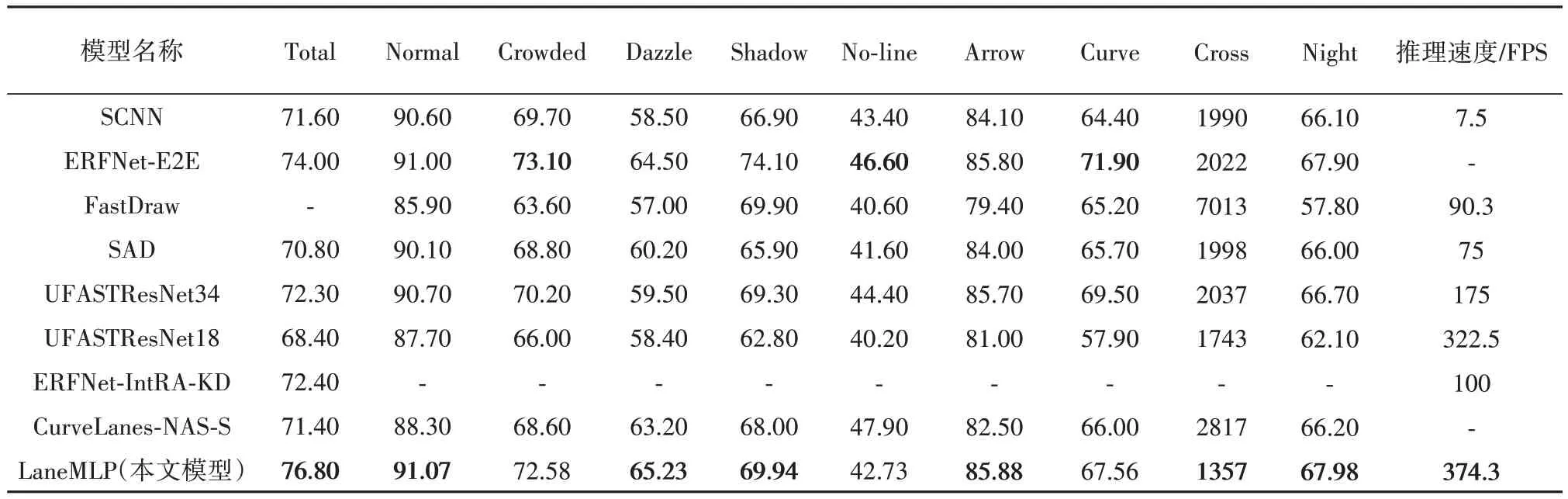
表4 各模型在CULane数据集上的准确率和推理速度Tab.4 Accuracy and speed of each model on CULane

CULane 数据集上的车道线检测结果如图9 所示，第一列为本文模型的预测结果，第二列为UFASTResNet18 模型的预测结果，从结果中可以看出：在结构损失函数的约束下，检测的车道线更加平滑，对于遮档部分的语义车道线也有较好的预测.

图9 在CULane数据集上的实验结果Fig.9 Experimental result on CULane

3 结束语

本文提出了一种利用MLP 网络进行车道线检测的新算法.该算法将MLP 网络应用于长线型预测任务，利用MLP 网络提取全局结构信息，提高模型的泛化性，同时结合组卷积，使用不同感受野的卷积核提取局部信息，提高了模型的推理准确率，实验表明MLP 进行长线型任务预测时有较好的全局特征提取能力，本文的模型在提高准确率的同时保持着较高的推理速度，根据实验结果，模型对炫光、夜间等环境的检测效果有着较为明显的提高，为车道保持辅助系统，车道偏离预警以及高级别的智能驾驶辅助系统提供了更多的选择.为使模型更具实用性，进一步简化模型结构，提高复杂环境的兼容性是下一步工作的重点.