平面单元和壳单元在复合有限条法中模拟加劲肋的应用

有限条法是20世纪70年代末提出的一种与有限元法(FEM)并行的数值计算方法，以其单元未知量少，计算效率高的优点受到国内外学者们的青睐.有限条法广泛应用于分析梁、板、柱等具有“条”特性的薄壁结构.传统的有限条法主要采用多项式(横向)和三角函数(纵向)的组合表示条单元的位移场，三角函数所对应的方向不存在结点，因此无法在此方向上布置加劲肋，而沿着纵向间隔布置加劲肋是梁构件中较为常见的情况.针对此类问题，样条有限条法能很好地解决长度方向上没有结点的问题.王宗木等提出双向样条函数模拟板结构以达到自由布置加劲肋的目的，但由于双向都是样条函数组成，所以该方法只适用于一块整体的平板结构，无法分析板之间存在一定角度的情况，不能分析梁构件.Chen等提出了一种复合有限条法，采用杆单元模拟加劲肋，并耦合加劲肋板的位移场，然而这种复合有限条法忽略加劲肋截面内的位移场，无法有效分析梁翼缘和加劲肋之间的相互作用关系，局限于不需要考虑加劲肋截面内位移的结构，如板结构.类似地，文献[18]基于Mindlin板理论和三次样条有限条法深入研究了加劲肋对夹层板屈曲的影响.这种方法采用梁单元模拟加劲肋，加劲肋附于板上，对应结点位移耦合，但是对于沿纵向布置加劲肋的梁截面，该方法无法考虑其翼缘和肋板的相互作用.文献[19]提出在复合有限条法中用梁单元模拟螺栓，连接组合截面，但由于梁单元无法考虑截面本身的位移特性，所以无法准确用于分析肋板.文献[20-21]深入探究了加劲肋对于薄壁轴力构件的屈曲影响.

鉴于此，本文采用基于样条有限条的复合有限条法，通过MATLAB自编程序实现模拟分析.加劲肋选择平面单元和壳单元来模拟，可以较容易地处理形态复杂的肋板，且能考虑到肋板与梁腹板、翼缘的相互作用.相比于壳单元，平面单元自由度、计算量相对较少，处理上也较为简便.因此，在加劲肋单元处理方面分别采用考虑平面内位移的平面单元和考虑平面内外位移的壳单元，深入研究在复合有限条法中平面单元能否准确模拟肋板的作用，进一步与壳单元模拟加劲肋的方法进行对比，验证其可靠性.

1 复合有限条法理论

复合有限条法将样条有限条和壳单元相结合，其中有限条单元用于模拟构件主体，壳单元模拟加劲肋.

进入2018年，随着国家市场监督管理总局的成立，国家食品药品监督管理总局的职责被整合其中，对外不再保留牌子，食品监督管理工作步入新阶段。

1.1 样条有限条

样条有限条横向采用多项式函数，纵向采用样条函数，位移场表现为两种函数的乘积.对于单个有限条单元，位移的方向即为横向，位移的方向即为纵向，如图1所示.采用Kirchhoff 板理论模型，4个自由度分别为、、、其中、由一次多项式和结线位移组合而成；为垂直于“条”面的位移，由经典的梁单元的型函数和面外结线位移、绕轴的转角组合而成此处结线位移是由样条函数沿长度方向分布的位移集合图1中、、为整体坐标系中的方向；、、为整体坐标系下3个方向的位移；为条横向宽度；、、、分别为结线1处4个方向的位移，同理，下标2代表节线2；、分别为两端均布荷载在结线1、2处的大小，通过应力、与截面厚度的乘积计算得到；、、代表局部坐标系；、、为局部坐标系下条单元3个方向的位移；为构件在纵向划分结点的数量、、的计算式如下：

(1)

(2)

(3)

需要注意的是，上述公式只是横向型函数，纵向即沿着长度方向采用3次等间距样条函数:

(4)

(2004-北京-20) 给定有限个正数满足条件T：每个数都不大于50且总和L=1275.现将这些数按下列要求进行分组，每组数之和不大于150 且分组的步骤是：首先，从这些数中选择这样一些数构成第一组，使得150与这组数之和的差r1与所有可能的其他选择相比是最小的，r1称为第一组余差；然后，在去掉已选入第一组的数后，对余下的数按第一组的选择方式构成第二组，这时的余差为r2；如此继续构成第三组(余差为r3)、第四组(余差为r4)，…，直至第N组(余差为rN)把这些数全部分完为止.

1.2 加劲肋单元

等参单元不会受到形状的局限，能够处理复杂的肋板，并且能考虑到肋板内部的位移变化以及与梁翼缘、腹板之间的相互作用.因此，采用等参平面单元和壳单元模拟较为复杂的加劲肋.平面单元和壳单元的型函数为

(5)

(6)

式中：、为绕、轴的转角自由度；、为节点绕、轴的转角自由度；、为自然坐标系下的坐标；、为自然坐标系点的坐标.

若为平面单元，只需考虑平面内位移，即参数变量只需要、两项；若为壳单元，则5项皆要考虑.

由于钻孔灌注桩使用的钻孔灌注设备的不同，其相应的施工工艺也不同，本文主要讨论循环钻机的施工工艺，具体如下：找平场地→测量并确定孔位→埋设防护桶→钻机设备到位→钻进→第一次先清孔→检测钻洞→制作钢筋笼→钻孔下导管→二次清孔→水下混凝土浇筑→拔管→桩基成型。

2)分析悬杯水平方向的运动速度和加速度变化规律，分别与原模型的运动参数进行比较，如图6和图7所示。在栽苗点处悬杯的速度达到最小值，有利于零速投苗，加速度变大，方向向后，说明悬杯对钵苗有向后的推力作用；此时速度与加速度曲线发生突变，说明悬杯开启非常快，即凸轮迅速由回程转到近休止位置，悬杯相对栽植器静止，绝对速度与加速度由栽植轮转动和机器前进运动所影响；悬杯闭合时，凸轮由近休止转到推程位置，由于推程段是等速运动规律，因此出现加速度的第二次突变，加速度达到最大值。因为推程段不会影响移栽机栽植质量，因此可以通过改进凸轮推程段来减小加速度的最大值。

面内位移对应的平面应变由下式计算得到：

(7)

弯曲产生的平面应变和切应变由下式计算得到：

(8)

式中：、分别为、方向正应变；为平面方向工程切应变；为应变矩阵；为位移向量；下标m、b、s分别代表平面项、弯曲项、剪切项；、同理.同样地，若为平面单元，只需要考虑平面应变项；壳单元则需要考虑平面应变、弯曲应变以及切应变项.

1.3 刚度组合

应变能公式为

如上所述，平面单元肋板和壳单元肋板对屈曲承载力结果影响很小可忽略不计，因此此处只对比有限元和复合有限条中平面单元肋板的差异结果.图7所示为不同长度构件有限元法和CSM2D的差异.从图中可以看出，有限元和复合有限条法的结果相差较小，无论是对于1个加劲肋、2个加劲肋及3个加劲肋，是轴力作用还是弯曲作用，最大差异值皆控制在5%以内，至少85%的构件屈曲承载力结果的差异值控制在2%以内.差异较大且波动相对明显的情况普遍是长度较小以局部屈曲为主的构件，但是与有限元的结果对比差距依旧控制在5%以内.平面单元和壳单元肋板之间的差异很小，因此有限元和有限条法在构件长度较短时产生的差异并非由于肋板单元的面外平动自由度引起，可能是条单元和壳单元存在一些转动自由度无法耦合以及Kirchhoff板理论不考虑厚度方向上的剪切变形的原因造成.

(9)

传统有限条法的屈曲分析选取的是截面最不利的情况，并沿长度方向均匀分布，复合有限条法依旧采用这种模式.有限条法与有限元法在边界处有所区别，为了便于对比，两者边界模式应该统一.两种方法皆在端部约束和方向位移，位移方向如图1所示其中限元法在跨中约束一个结点的向位移以保证约束完整性，边界条件如图3所示.材料弹性模量为200 GPa，泊松比为0.3.有限元模型采用shell181单元.

1.4 屈曲计算

弹性屈曲分析的求解方程为

如果你正在为圣诞夜准备Party，那么不要错过4号“狂徒西拉干红葡萄酒”和5号“狂欢赤霞珠干红葡萄酒”。无论是充满青春活力的酒标，易饮的口感，还是零售价118元超高的性价比，都非常适合派对达人，喝不完还可以用来做圣诞热红酒！当然，你唯一需要担心的就是酒太好喝，一不小心就梦了周公。

(+λ)=

(10)

式中：、分别为构件主体和加劲肋组合的弹性刚度矩阵以及几何刚度矩阵；为屈曲系数；为屈曲变形值.

2 复合有限条计算模型

基于所选加劲肋的情况，在复合有限条法中分别采用平面单元肋板和壳单元肋板，深入探讨平面单元和壳单元对屈曲结果的影响.槽钢高80 mm，宽40 mm，厚2.5 mm，加劲肋与构件高宽相同，厚度为1 mm.分析两种荷载(轴力和弯矩)条件下，单个加劲肋、2个加劲肋和3个加劲肋的情况对两种肋板单元的屈曲承载力的影响.图6所示为轴力作用和纯弯曲作用下，采用平面单元肋板和壳单元肋板计算的构件屈曲承载力结果对比，图中为屈曲荷载；为屈曲弯矩;CSM3D为壳单元复合有限条法；CSM2D为平面单元复合有限条法.两种方法得到的屈曲承载力几乎一致.加劲肋数量增加在一定程度上能提高屈曲承载力，主要表现为改善局部屈曲构件的承载力.但是对于整体屈曲的构件，加劲肋对承载力的提高较局限.表3所示为平面单元和壳单元肋板之间的差异平均值，此处考虑到差异值平均存在正负抵消的情况，故采用所有差异的绝对值平均.发现加劲肋数量对两种单元之间差异值大小不存在正增长的关系，但是整体而言，2个加劲肋或者3个加劲肋比单加劲肋的差异值要大.受力类型对于差异值大小没有明确的影响.差异值最大为0.07%(为3个加劲肋在轴力作用下的情况)，几乎可以忽略不计.综上，平面单元和壳单元肋板的差异整体很小，荷载类型和加劲肋的数量对差异值没有明确的影响.

对于复合有限条法模型，当<2 000 mm 时，纵向划分20等份；≥2 000 mm 时，划分40等份.当<50 mm时，横截面网格为10 mm；≥50 mm 时，横截面网格为20 mm.需要注意卷边槽钢的卷边与横截面网格大小相近，因此横截面网格需根据卷边长度做具体调节.对于有限元模型，当<80 mm时，网格大小选2 mm；当≥80 mm时，网格大小选 5 mm.

2.1 复合有限条和有限元计算模型对比

式中：为应变向量，对应、、；为应力；应变矩阵对应、、；位移向量对应、、；为材料本构方程；为刚度矩阵.通过式(9)获得样条单元和壳单元(平面单元)的刚度矩阵.壳单元的刚度需要通过雅可比矩阵转换到物理坐标系下进行高斯积分计算.条单元和壳单元(平面单元)的刚度矩阵通过角度变换由局部坐标系转到整体坐标系，然后进行“条”与“壳”单元的刚度矩阵组合.

2.2 复合有限条法网格分析

复合有限条法网格大小与有限元网格大小对于屈曲结果影响略有分别.复合有限条法中弯曲部分采用三次多项式函数和三次样条函数的乘积，精度会高于有限元壳单元，因此网格尺寸大于壳单元尺寸即能达到一定精度.以槽钢单肋板和三肋板为例，研究网格大小对复合有限条法计算精度的影响.图4所示为纵向网格数量对于精度的影响，图中为纵向网格划分数量；为构件的承载力与不同网格下该构件承载力最小值的比值.考虑到不同长度的构件承载力差别很大，在同一对比图中承载力小的构件的变化趋势容易被掩盖，纵坐标设置为该构件的承载力与不同网格下该构件承载力最小值之比，可以统一变化趋势数量级.选取构件长度=80，50及 1 000 mm，横向网格大小为20 mm.当>20时，承载力值逐渐趋于稳定.纵向网格对于承载力的影响十分有限，对比网格等分数量为8和80的情况，发现两者承载力结果差别最大的情况为1.06%，其余情况不到0.2%.

图5所示为横向网格对于精度的影响，图中为横向网格划分大小.选取=80，500，1 000 及 2 000 mm，纵向网格为20等份.当<20 mm时，承载力结果逐渐收敛.对比网格为40、5 mm的情况，发现两者承载力差距最大为15%.而网格 20 mm 和 5 mm 对比，差距最大为1%左右.基于计算效率和精度，20 mm 是比较好的横截面网格的选择.

县级山洪灾害防御预案包括各县级行政区自然和经济社会基本情况，山洪灾害类型，历史山洪灾害损失情况，山洪灾害的成因及特点；县级山洪灾害防御部门职责及责任人员；区域内有山洪灾害防治任务乡（镇）的防灾任务、要求和山洪灾害防御措施；监测站网布设，预警对象、等级、程序和方式；转移安置、抢险救灾及灾后重建，日常的宣传及演练等要求。

古希腊是一种热衷于美德的时代，所以，人们热衷于思考以什么样的教育方式才能最好地促使人们获得美德。美德，是人们使自己成为一个好人，获得心灵品质的提升，从而能过一种好生活的主体素质，也体现了古希腊人对人的应然形象(当然主要是理想的希腊人)的一种理解。亚里士多德对这种理解提供了一个最为完整、最为实际的思路，他把苏格拉底式的独立于政治的知识精英姿态调整为与政治密切合作的立场，从而既可以基于实践理性来思考什么样的政体能够使人们既成为一个好公民又成为一个好人，又可以思考我们应该如何使各种现实政体得以完善，使之发挥塑造人们的完整美德的作用，从而使人们能过上一种大多数人可以平凡拥有的好生活。

3 平面单元和壳单元模拟横向肋板对比

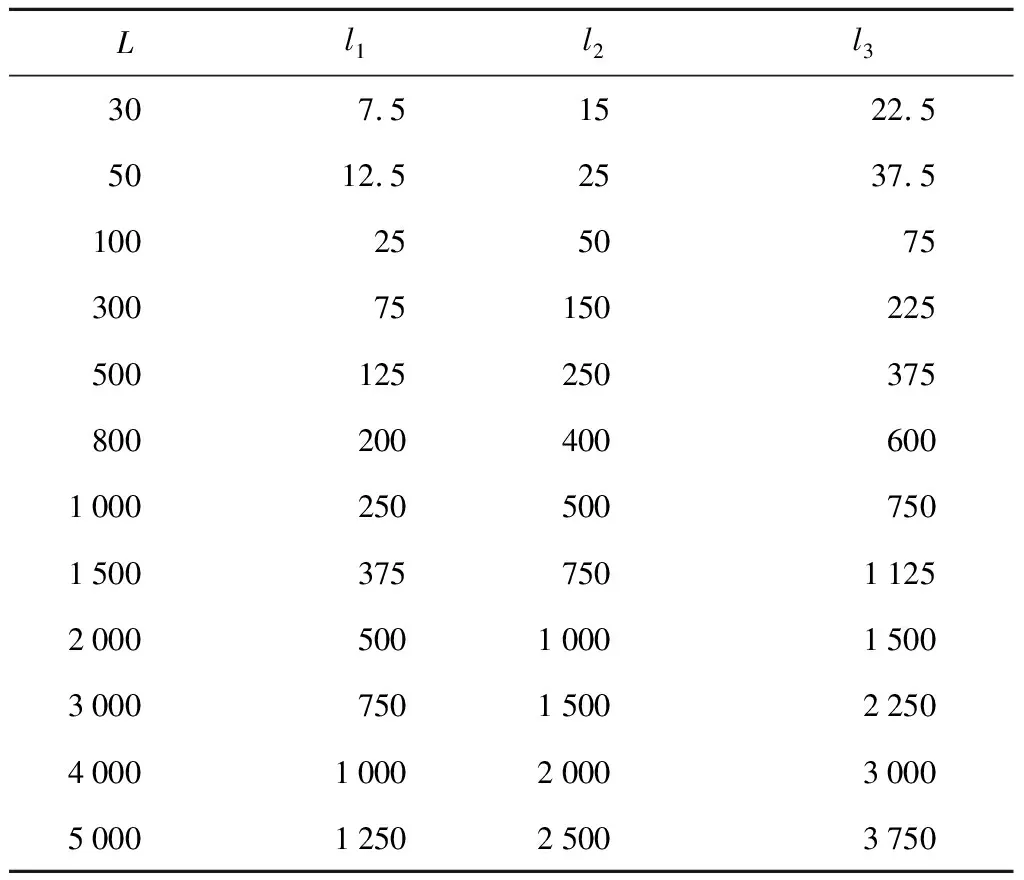
为了对比槽钢和卷边槽钢在轴应力作用下和纯弯曲应力作用下两种加劲肋单元的区别，选取不同长度的构件分别布置1个加劲肋、2个加劲肋和3个加劲肋进行屈曲分析.单个加劲肋设置在构件中间的位置，2个加劲肋设置在三等分点的位置，3个加劲肋设置网格划分取整，在四等分点的位置.2个加劲肋和3个加劲肋考虑到网格划分取整，具体选取如表1、2所示，表中、、分别代表第1个加劲肋、第2个加劲肋及第3个加劲肋到构件一端的距离.

3.1 槽钢计算结果对比分析

构件的受力采用有限条法中通用的受力形式，如图1所示.基于上述应力假设，应力沿着长度方向均匀分布.对于没有肋板的情况，首先计算出截面的应力分布，根据计算出的应力沿长度方向均匀施加，最后由式(10)求解屈曲特征值.对于有肋板的情况，需要考虑肋板的应力分布，分析相对复杂.首先需计算得到截面应力分布，然后通过静力分析得到肋板的应力分布.考虑到静力分析之后加劲肋对构件(除去加劲肋)本身的应力变化影响不大，因此在进行屈曲分析时构件主体的部分直接用最初施加的应力分布，加劲肋则用静力分析得的应力分布，基于势能公式得到几何刚度矩阵，通过式(10)计算出屈曲特征值.分析研究基于MATLAB自编程序，程序流程如图2所示.

3.2 卷边槽钢计算结果对比分析

构件的截面与肋板之间的关系大致可以分为两类情况：三边接触和四边接触.鉴于3.1节中槽钢截面差异值很小，将分析拓展到卷边槽钢，其他截面不另作对比分析.卷边槽钢高为100 mm，翼缘宽为 60 mm，厚2 mm，卷边长度为10 mm.加劲肋与构件高宽相同，厚度为1 mm.由于差异值与肋板数量没有非常明确的关系，卷边槽钢算例只选取单肋板和双肋板的情况.图8所示为不同作用力下CSM2D和CSM3D计算的承载力曲线.对比看出平面单元和壳单元肋板得到的卷边槽钢的屈曲承载力非常接近.和槽钢一样，加劲肋主要提升以局部屈曲或畸变屈曲为主的构件的承载力，对于整体屈曲构件作用很小.表4所示为轴力和纯弯曲应力作用下平面单元肋板和壳单元肋板的误差.通过对比表3、4发现，相比于比槽钢，卷边槽钢中平面单元肋板和壳单元肋板的差异绝对平均值较大，但是仍然保持在一个较小的范围(0.75%以内).

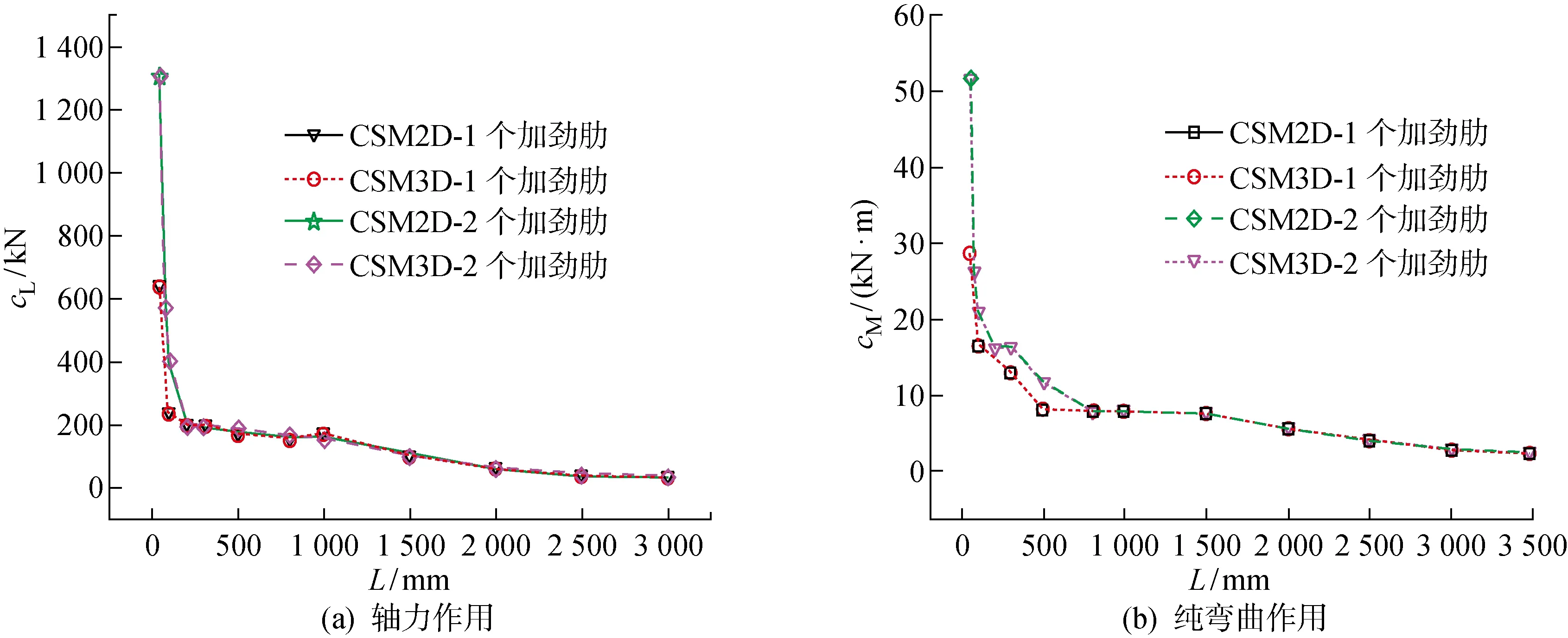
图9、10所示为轴力作用下3种方法的屈曲模态对比，图中′为相对位移.可见，轴力作用下3种方法得到的屈曲模态几乎一致，即复合有限条法对于这类截面的分析是比较精确的.

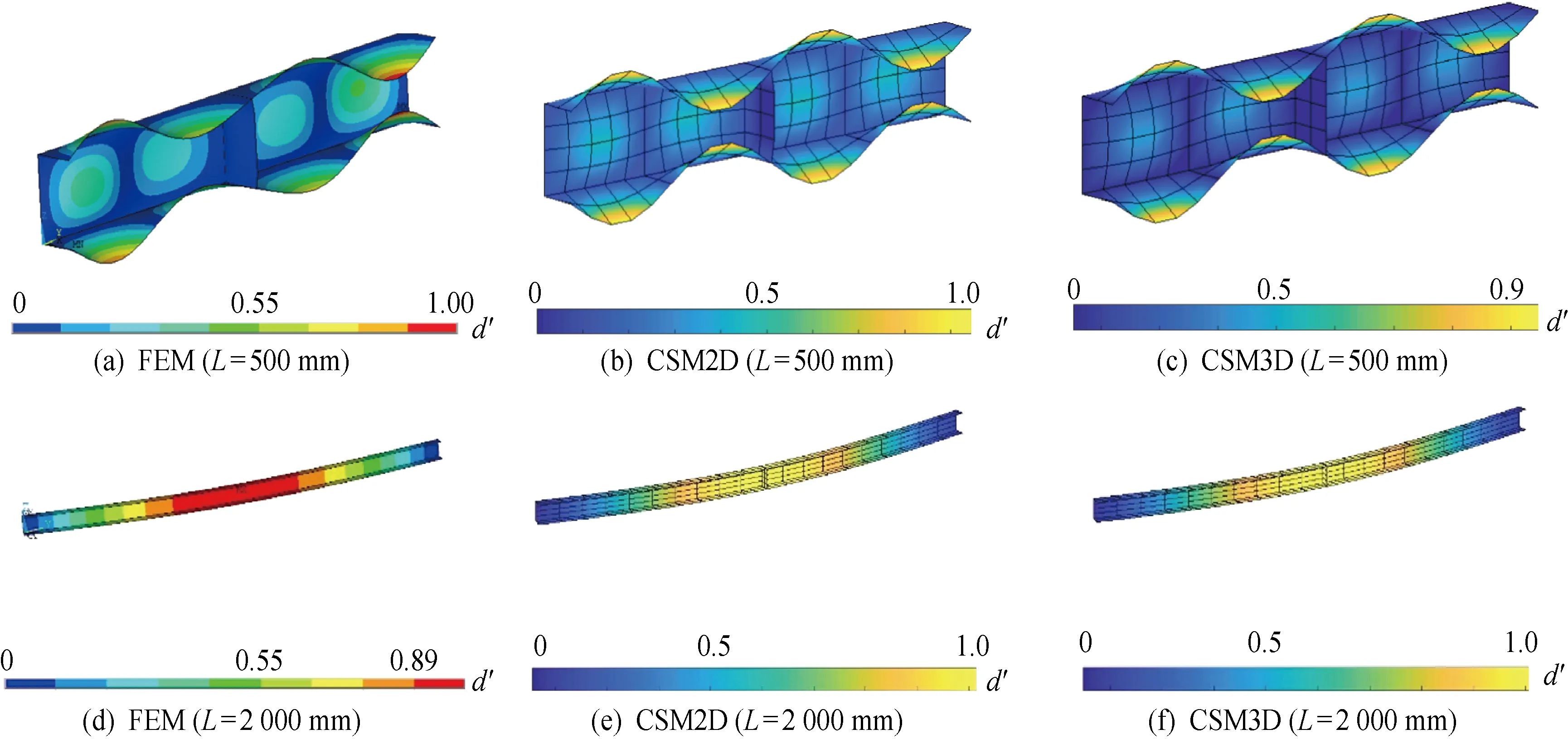
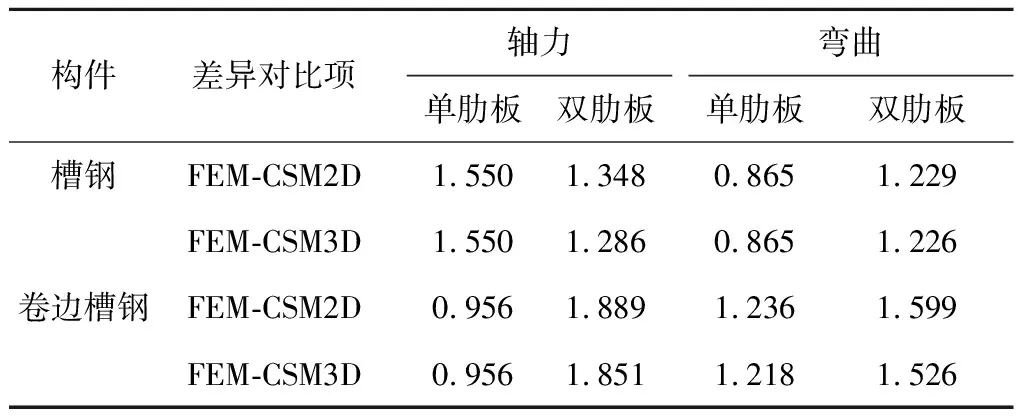
图11、12所示为有限元和两种复合有限条法的差异曲线，可以看出壳单元加劲肋的复合有限条法CSM3D与有限元的差异并不是一直小于平面单元加劲肋的复合有限条法CSM2D和有限元的差异.复合有限条法(平面单元加劲肋和壳单元加劲肋)与有限元的差异值始终控制在5%以内，71%的情况控制在3%以内.对于单肋板，<1 000 mm时，主要对应局部屈曲或畸变屈曲，差异波动相对明显；>1 000 mm时，主要对应整体屈曲情况，差异波动会逐渐平稳.双肋板情况类似，<1 500 mm 时，主要对应局部屈曲和畸变屈曲的长度，差异波动相对明显；>1 500 mm时，差异波动会逐渐稳定.图13对比了FEM、CSM2D及CSM3D的屈曲模态，结果非常吻合.考虑到差异值相对大于槽钢，所以继续将平面单元肋板和壳单元肋板的情况分别与有限元的结果进行对比，以校核两类复合有限条法的可靠性.

表5所示为有限元和两种复合有限条法的屈曲承载力的平均绝对差异值，就整体而言，FEM-CSM3D的差异比FEM-CSM2D的差异略微小，但是也存在一些情况FEM-CSM3D差异稍大，例如轴力作用下单加劲肋卷边槽钢和弯矩作用下单肋板槽钢.总体而言，FEM-CSM2D的差异值与FEM-CSM3D的差异值相差很小，都控制在5%以内.相对于壳单元加劲肋，平面单元能在一定程度提高运算效率并降低运算的复杂度.

4 平面单元与壳单元模拟加劲肋计算效率对比

影响计算效率的主要因素是自由度的数量.无论对于壳单元还是平面单元模拟加劲肋的情况，条单元自由度数量是相同的，而产生影响的主要是加劲肋的自由度.加劲肋自由度直接影响刚度矩阵大小从而影响矩阵计算、组合和求解的时间.以轴力作用下槽钢为例，分别采用不同加劲肋数量以及不同网格大小来分析两种单元的计算效率差别.计算时间是从参数输入到后处理所用的时间.

图14所示为不同条件下两种加劲肋单元计算的效率对比，图中为CSM2D和CSM3D计算时间的比值.图14(a)比较了不同数量加劲肋下平面单元和壳单元的计算时间的比值.可以明显看出，平面单元计算时间比壳单元计算时间要短.随着加劲肋数量增多，平面单元计算效率的优越性逐渐彰显.1个加劲肋、2个加劲肋、3个加劲肋的情况下，二者时间比值平均值分别为0.95、0.86、0.73.图14(b)比较了不同的网格划分下平面单元和壳单元的计算时间比.纵向划分数量增倍对于两者计算时间差并不是很明显，而横截面网格划分增倍平面单元计算时间明显短于壳单元.网格划分横向8份×纵向20份、横向 8份×纵向40份和横向16份×纵向20份的情况下，二者时间比平均值分别为0.95、0.96、0.79.其中横向为横截面，纵向为长度方向.本质上，复合有限条法计算效率与自由度相关，无论是加劲肋数量增加还是横截面网格增加都直接会影响加劲肋网格数量，从而影响到总的自由度数量.通过对比可知，随着加劲肋网格数量增多，平面单元模拟加劲肋计算效率比壳单元更高，而且差异会逐渐明显.

5 结论

基于Kirchhoff 板理论的复合有限条法，提出了采用平面单元和壳单元模拟加劲肋的数值分析方法，并对比了运用平面单元和壳单元模拟肋板对屈曲分析结果的影响，得到如下结论：

根据上述实验可知，一是通过安全、高产、高效栽培的应用效果可看安全、高产、高效栽培栽培处理可以提高单位面积水稻有效穗数、结实率及每穗实粒数，可极大增加产量，增产幅度可达30%左右。二是在2014年气象情况下处理1、处理2、处理3、处理4均有较好表现，作为栽模式具有通用性；从品种的抗倒、耐肥能力看龙粳38强于龙粳40。三是在确保农时的前提下即壮苗适期早插的条件下，安全高产高效栽培在胜利农场是可行的。

(1)复合有限条法弥补了传统有限条法无法考虑横向加劲肋的不足.与有限元法结果对比，发现两种复合有限条法与有限元的屈曲承载力差异值控制在5%以内，满足所需要的精度，并且屈曲模态吻合良好.

(2)通过对比不同构件长度、不同截面类型和不同加劲肋数量以及在不同外力作用下的屈曲承载力的差异范围，发现加劲肋面外平动自由度对于屈曲分析结果影响较小，复合有限条法中平面单元模拟加劲肋和壳单元模拟加劲肋结果十分接近(相差0.75%以内)，且平面单元自由度更少，计算效率更高.采用平面单元模拟加劲肋即可满足预期.

(3)加劲肋主要提升局部屈曲或者畸变屈曲的构件屈曲承载力，对于整体屈曲的构件加劲肋的作用很小.构件以局部屈曲或者畸变屈曲为主的情况，有限元和复合有限条法的差异波动相对明显.

对“工作经验”字段的取值进行整理，有经验要求的招聘信息共6 245条，占总数的91.49%。其中，教育机构类对经验作出较低的要求，多为“1-2年”；营销与贸易类与技术类岗位对经验要求较高，“3-5年”占比最高。

汽车悬架构件是悬架系统的基础。一个完整的悬架总成，其组件构成如图2所示：弹性元件(弹簧)—吸收来自路面的冲击。阻尼元件(减振器)—通过限制弹簧的振动来改善乘坐的舒适性。稳定器(横向稳定杆或侧倾稳定杆)—防止车辆横向摆动。导向机构—使上述部件保持就位和控制车轮的纵向或横向运动。

(4)网格划分大小会影响最后的屈曲承载力结果.复合有限条法中纵向网格数量对于承载力影响较小，而横截面网格大小对于结果影响比较明显.复合有限条法截面内网格基本为20 mm，纵向网格数量为20等份，对于长度较大或者较小的构件以及卷边的影响，会具体细分.有限元网格基本选取的是 5 mm 的大小，对于长度小于80 mm的构件选用 2 mm，复合有限条法网格和自由度数量显著少于有限元法，计算效率更高.

(5)相比于槽钢的情况，卷边槽钢中平面单元肋板和壳单元肋板之间屈曲承载力的差异值较大.