(m,5,2,4)光正交码最大容量的一种计算方法
2022-06-30卢晓立黄月梅
卢晓立,黄月梅,2
(1.内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022;2.内蒙古自治区应用数学中心,内蒙古 呼和浩特 010022)
1 相关引理
设m,k,λa,λc为正整数,Zm为模m的剩余类加群,参数为(m,k,λa,λc)光正交码是一些长为m,汉明权重为k的(0,1)-序列的集合C,每个(0,1)-序列称为一个码字,且满足下列性质:
(1)自相关性:对于任意A=(ai)∈C 与任意正整数r,r∈Zm{0},有
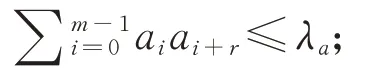
(2)互相关性:对于任意A=(ai),B=(bi)∈C 与任意整数r,r∈Zm,A≠B,有
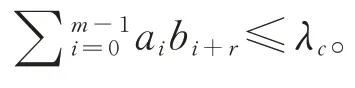
公式中的角标模m运算。一个参数为(m,k,λa,λc)光正交码,简记为(m,k,λa,λc)-OOC,所含的码字个数称为容量。对给定的正整数m,k,λa,λc,常用Φ(m,k,λa,λc)表示所有参数为(m,k,λa,λc)的光正交码中最大的容量。达到最大容量的光正交码为最优。
光正交码最早在文献[1]中被研究。起初,各学者主要是对λa=λc的光正交码进行研究。关于λa≠λc的情况,在文献[2]中,给出了k=4,λa=1和2,λc=3 时的一维以及二维光正交码的最优值。在文献[3]中,确定了k,λa=k-2,λc=k-1 的最优二维光正交码的码字个数的计算公式,并给出了k=5,λa=3,λc=4的最优二维光正交码的码字个数的确切值。
本文确定了k=5,自相关系数为3 时的光正交码的轨道代表元的表示形式,并且进一步给出了一种求解k=5,λa=2,λc=4 的一维光正交码的最大码字个数的计算方法。
令In={0,1,2,…,n-1},Zm是模m的剩余类加群,集合Ω(n×m,k)为In×Zm的所有k元子集的集合。Φ(n×m,k,λa,λc)表示参数为(n×m,k,λa,λc)的二维光正交码的最大容量。
引理1[2]设n,m,k,α为正整数,且1 ≤α≤k-2,则
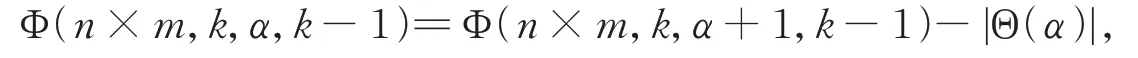
Θ(α)是集合Ω(n×m,k)在群Zm作用下满足λ(X)=α+1 时的所有轨道的集合。
故当n=1,k=5,α=2 时,结论如下。
推论对任意正整数m,有Φ(m,5,2,4)=Φ(m,5,3,4)-|Θ(2)|。
结合文献[3]中给出的结果,只需确定Θ(2)的值,即集合C5Zm在群Zm作用下满足λ(X)=3 时的所有轨道的个数。
2 预备知识
Zm是模m剩余类加群。令CkZm表示Zm中所有k‐子集的集合。对于C中的任意一个(0,1)‐序列A,相应地,在Zm上有且仅有一个k‐子集XA,使得i∈XA当且仅当A的第i个位置为1。根据上述条件,可以得到光正交码的一个等价定义,即一个汉明权重为k的一维光正交码可以看成一些k‐子集的集合{XA:A∈C },每个k‐子集也称作区组。反之,设B ⊆CkZm,则B 构成一个汉明权重为k的一维光正交码要满足:
(1)自相关性:对任意的区组X∈B 和任意的i∈Zm{0},|X∩(X+i)|≤λa;
(2)互相关性:对任意的区组X,Y∈B,X≠Y和任意的i∈Zm,|X∩(Y+i)|≤λc。
其中对于任意X∈B,有X+i={x+i:x∈X},所有加法在Zm上进行。
对于任意k‐子集X∈CkZm,定义X的差集为多重集ΔX={a-b(mod m):a,b∈X,a≠b}。定义ΔX的支撑为ΔX中所有互异元素组成的集合,记作supp(ΔX)。此外定义λ(X)为ΔX中出现最多次的差值的次数,则有λ(X)=max {mi(ΔX):i∈ΔX},其中mi(ΔX)表示正整数i在差集ΔX中出现的重数。再由 光正交码的码字与k‐子集之间的关系,得λ(X)=max {|X∩(X+η)|:η∈Zm{0}}。对任意X∈CkZm和任意i∈Zm,在Zm作用下,结合定义X+i={x+i:x∈X},集合{X+i:i∈Zm}称为X∈CkZm的轨道。X的轨道记作O(X)。若轨道O(X)中有m个互异的元素,则称为长轨道;反之,称为短轨道。在群Zm作用下,CkZm中的k‐子集被划分成了一些轨道。这些轨道代表元构成了对应的光正交码。
3 关于Θ(2)值的计算
设θ是在群Zm作用下的任意轨道,若X,Y∈θ,则ΔX=ΔY。于是,假定轨道θ的一个代表元X={0,x1,…,xk-1}。
引理2对于(m,5,k,4)-OOC,满足λ(X)=3 的码字集Θ(2)可以写成互不相交的轨道集的并集,即,具体分类为
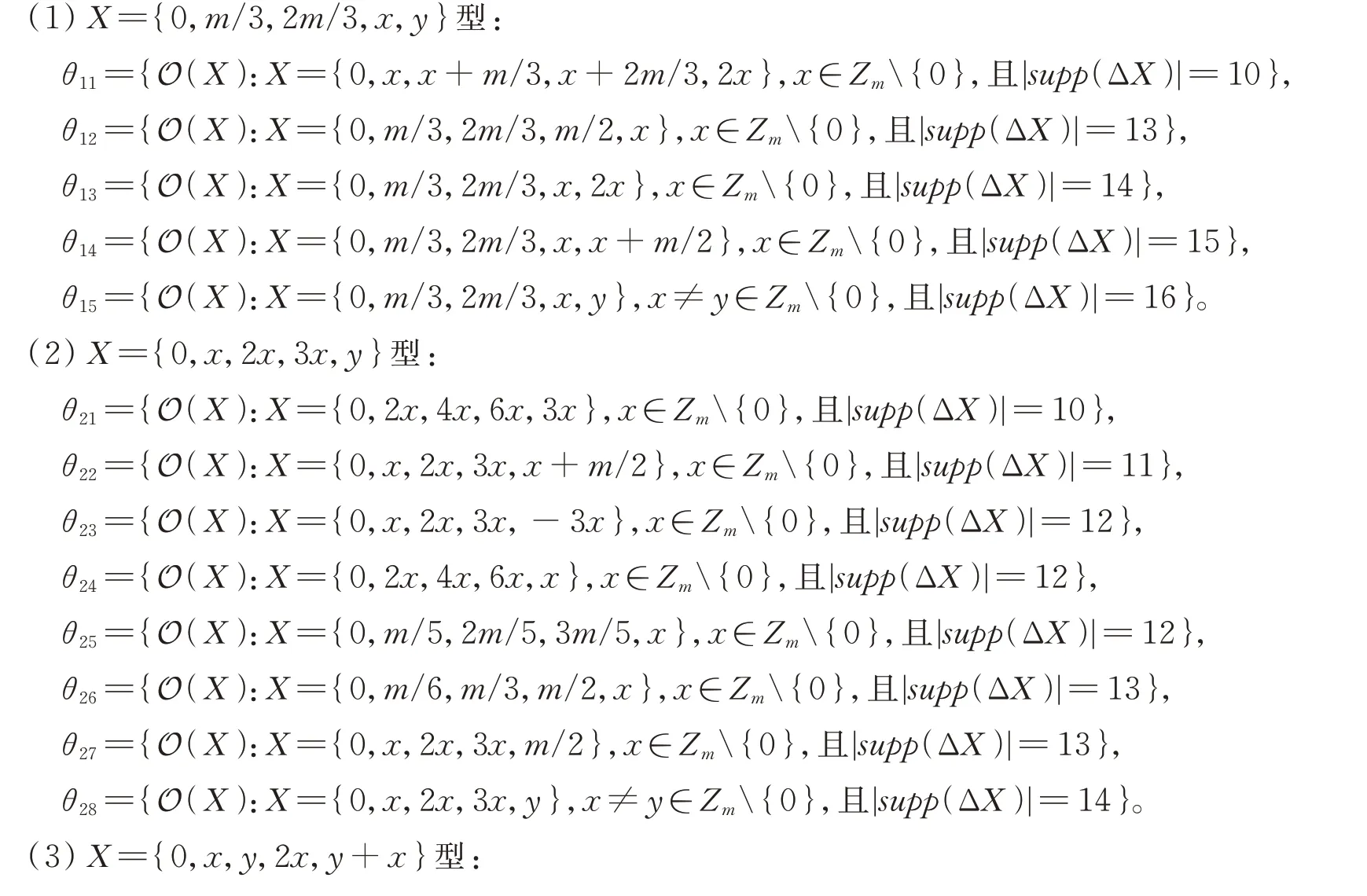

以下为确定上述各集合的值。
引理3设m是正整数,若3|m,则|θ11|=[m/2]-ϵ,其中ϵ是当γ∈{4,6,9}时,满足γx≡0(mod m)的互不相同的正整数x∈(0,[m/2])的个数。否则为0。
证明由集合θ11的定义,若3 ∤m,则|θ11|=0;若3|m,设θ是集合θ11中的任意轨道,则θ=O(X),其中X={0,x,x+m/3,x+2m/3,2x},x∈(0,m)且|supp(ΔX)|=10。故得ΔX={±m/3,±m/3,±m/3,±x,±x,±2x,±(x+m/3),±(x+2m/3),±(x-m/3),±(x-2m/3)},且±2x,±(x+2m/3),±m/3,±x,±(x+m/3)互不相同,详细计算得γx≡0(mod m),γ∈{4,6,9}。另一方面,设X′={0,x′+2m/3,x′+m/3,x′,2x′} 与X在同 一轨道,则ΔX′=ΔX,即{±2x′,±x′,±(x′+m/3),±(x′+2m/3)}={±2x,±x,±(x+m/3),±(x+2m/3)}。详细计算得到X′ 与X属于同一条轨道当且仅当x′=x,-x。由此x∈(0,[m/2]),故|θ11|=[m/2]-ϵ,ϵ是当γ∈{4,6,9}时,满足γx≡0(mod m)的互不相同的正整数x∈(0,[m/2])的个数。
引理4设m是正整数。
(1)若6|m,则|θ12|=m-1-ϵ,ϵ 为满足12x≡0(mod m)的正整数x∈(0,m)的个数。否则为0。
(2)若3|m,则|θ13|=m-1-ϵ,ϵ是 当γ∈{9,12} 时,满 足γx≡0(mod m) 的 互 不 相 同 的 正 整 数x∈(0,m)的个数。否则为0。
(3)若6|m,则|θ14|=(m-1-ϵ)/6,ϵ 为满足12x≡0(mod m)的正整数x∈(0,m)的个数。否则为0。
证明与引理3 的证明类似,此处略。
引理5设m是正整数。当m为奇数时,则有
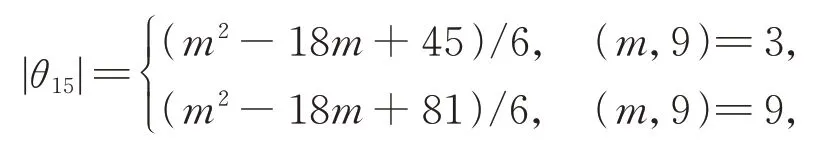
当m为偶数时,则有
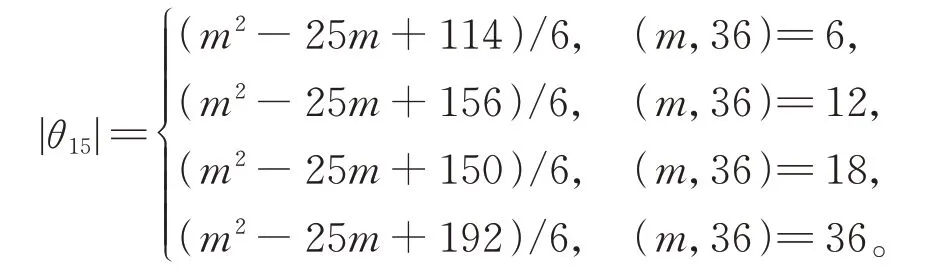
证明由集合θ15的定义,若3 ∤m,则|θ15|=0。若3|m,设θ是集合θ15中的任意轨道,则θ=O(X),其中X={0,m/3,2m/3,x,y},x≠y∈(0,m)且|supp(ΔX)|=16。故ΔX={±m/3,±m/3,±m/3,±x,±y,±(y-x),±(x-m/3),±(x-2m/3),±(y-m/3),±(y-2m/3)} 且±m/3,±x,±y,±(xm/3),±(x-2m/3),±(y-m/3),±(y-2m/3),±(y-x) 互 不 相 同,详 细 计 算 得2x≡a(mod m),a∈{m/3,2m/3,0},y ≡b(mod m),b∈{±x,±x+m/3,±x+2m/3,2x,2x-m/3,2x-2m/3,x+m/2,m/3,2m/3},2y≡c(mod m),c∈{0,x,x+m/3,x+2m/3,m/3,2m/3}。设E={(x,y):x≠y∈(0,m),2x≡a(mod m),a∈{0,m/3,2m/3},y ≡b(mod m),b∈{±x,±x+m/3,±x+2m/3,2x,2x-m/3,2x-2m/3,m/3,2m/3,x+m/2},2y≡c(mod m),c∈{0,x,x+m/3,x+2m/3,m/3,2m/3}},则存在(x,y)∈E使 得 任 意 轨 道θ∈O(x,y),其 中O(x,y)=O({0,m/3,2m/3,x,y}),定 义 集 合E到θ15的 映 射τ:任 意(x,y)∈E有(x,y)→O(x,y),显 然τ是 一 个 满 射。故 对 任 给 的θ∈θ15,下 面 计 算τ-1(θ) 的 大 小。对(x,y)∈E有θ=O(x,y)。 若 (x′,y′)∈τ-1(θ), 则O(x,y)=O(x′,y′), 存 在t∈Zm使 得{0,m/3,2m/3,x,y}={0,m/3,2m/3,x′,y′}+t, 显 然t∈{0,m/3,2m/3,x,y}。 若t=x, 则{0,m/3,2m/3,y}={x+m/3,x+2m/3,x+x′,x+y′},因 此x+m/3 或x+2m/3 ∈{0,m/3,2m/3,y},这种 情 况 不 存 在,同 理t≠y,故t=0,m/3,2m/3。 详 细 计 算 得 到X′与X在 同 一 轨 道 当 且 仅 当(x′,y′)∈B(x,y)={(x,y),(x+m/3,y+m/3),(x+2m/3,y+2m/3),(y,x),(y+m/3,x+m/3),(y+2m/3,x+2m/3)}。验证得τ-1(θ)=B(x,y)。于是有|θ15|=|E|/6。
计 算|E|。E1={(x,y):x≠y∈(0,m),2x≡a(mod m),a∈{0,m/3,2m/3}},E2是E1的 子 集,满 足y≡b(mod m),b∈{±x,±x+m/3,±x+2m/3,2x,2x-m/3,2x-2m/3,x+m/2,m/3,2m/3},2y≡c(mod m),c∈{0,x,x+m/3,x+2m/3,m/3,2m/3},根据E的定义,|E|=|E1|-|E2|,
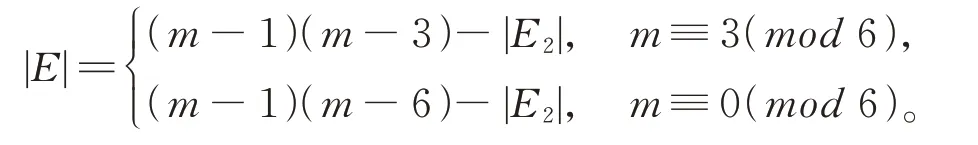
计 算 |E2|。m≡3(mod6),设 集 合M={m/3,2m/3},E2={(x,y):x≠y∈(0,m),y∈Rx}。x∈(0,m)M且x取 奇 数 或 者 偶 数 时 有:Rx奇=[1,m- 1]∩{m/3,2m/3,±x,±x+m/3,±x+2m/3,2x,2x-m/3,2x- 2m/3,(x+m)/2,(3x+m)/6,(3x+ 5m)/6};Rx偶=[1,m- 1]∩{±x,±x+m/3,±x+2m/3,2x,2x-m/3,2x- 2m/3,x/2,(3x+ 4m)/6,(3x+ 2m)/6,m/3,2m/3}。 任 意x∈(0,m)M有

由此得
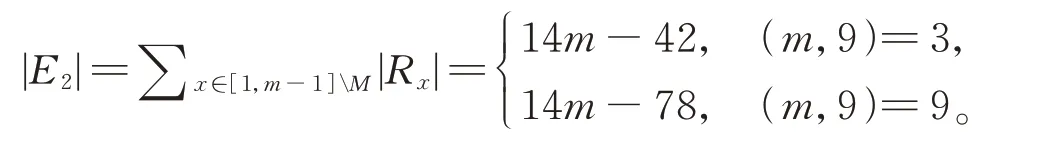
m≡0(mod6),设集合M={m/2,m/3,2m/3,m/6,5m/6},则E2={(x,y):x≠y∈(0,m),y∈Rx}。x∈(0,m)M且x取 奇 数 或 者 偶 数 时 有:Rx奇=[1,m-1]∩{±x,±x+m/3,±x+2m/3,2x,2xm/3,2x-2m/3,m/3,2m/3,m/6,5m/6,x+m/2,m/2};Rx偶=[1,m-1]∩{±x,±x+m/3,±x+2m/3,2x,2x-m/3,2x-2m/3,x+m/2,x/2,(3x+4m)/6,(3x+2m)/6,(x+m)/2,(3x+m)/6,(3x+5m)/6,m/2,m/3,2m/3,m/6,5m/6}。则|Rx|分别为
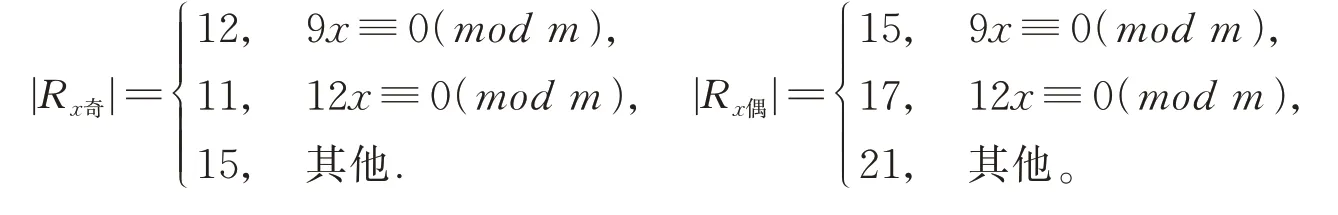
由此得
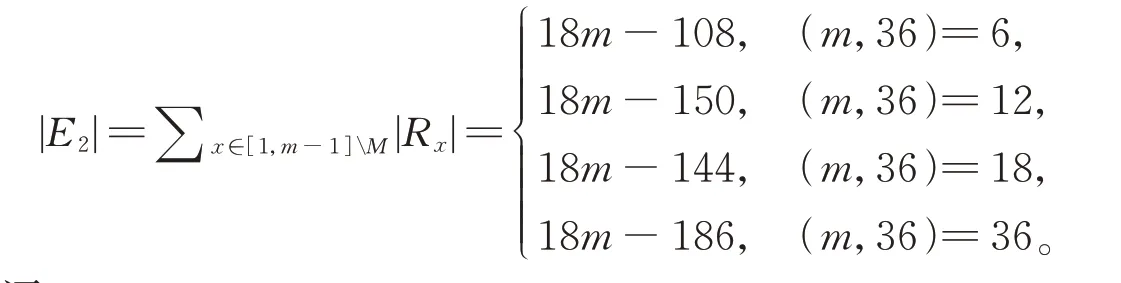
结合|E1|,结论得证。
引理6设m是正整数,则|θ21|=[m/2]-ϵ,ϵ是γ={7,8,9,10,12}时,满足γx≡0(mod m)的互不相同的正整数x∈(0,[m/2])的个数。
证明注意到X与-X在同一轨道,故设θ是集合θ21中的任意轨道,则θ=O(X),其中X={0,2x,4x,6x,3x},x∈(0,[m/2])且|supp(ΔX)|=10。之后的证明思路同引理3 的证明,此处略。
引理7设m是正整数。
(1)若2|m,则|θ22|=m-1-ϵ,ϵ是γ∈{6,8,10} 时,满 足γx≡0(mod m) 的 互 不 相 同 的 正 整 数x∈(0,m)的个数。否则为0。
(2)|θ23|=|θ24|=m-1-ϵ,ϵ是γ∈{7,8,9,10,11,12} 时,满足γx≡0(mod m) 的互不相同的正整数x∈(0,m)的个数。
(3)若(m,10)=5,则|θ25|=m-5;若(m,10)=10,则|θ25|=m-10。否则为0。
(4)若(m,12)=6,则|θ26|=m-6;若(m,12)=12,则|θ26|=m-12。否则为0。
(5)若2|m,则|θ27|=m-1-ϵ,ϵ是γ∈{8,10,12} 时,满 足γx≡0(mod m) 的 互 不 相 同 的 正 整 数x∈(0,m)的个数。否则为0。
证明思路类似于引理3,此处略。
引理8设m是正整数,当m为奇数时,则有
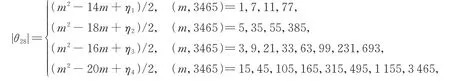
其中

当m为偶数时,则有

其中

证明与引理5 的证明类似,此处略。
引理9设m是正整数,则
(1)|θ31|=m-1-ϵ,ϵ是 当γ={6,7,8,9,10} 时,满 足γx≡0(mod m) 的 互 不 相 同 的 正 整 数x∈(0,m)的个数。
(2)|θ32|=m-1-ϵ,ϵ是 当γ={6,7,8,9,10} 时,满 足γx≡0(mod m) 的 互 不 相 同 的 正 整 数x∈(0,m)的个数。
(3)若(m,8)=4,则|θ33|=m-4;若(m,8)=8,则|θ33|=m-8。否则为0。
证明类似于引理3 的证明,此处略。
引理10设m是正整数,当m为奇数时,则有
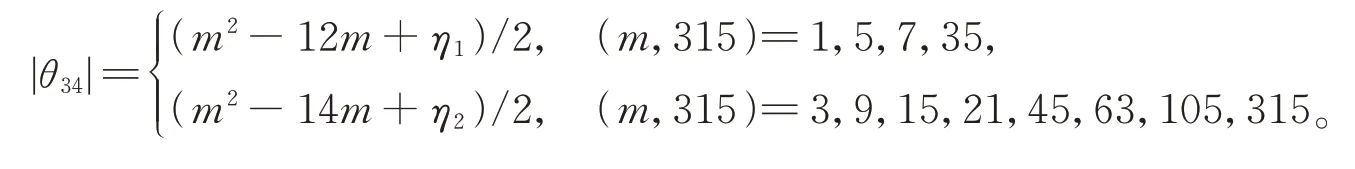
其中
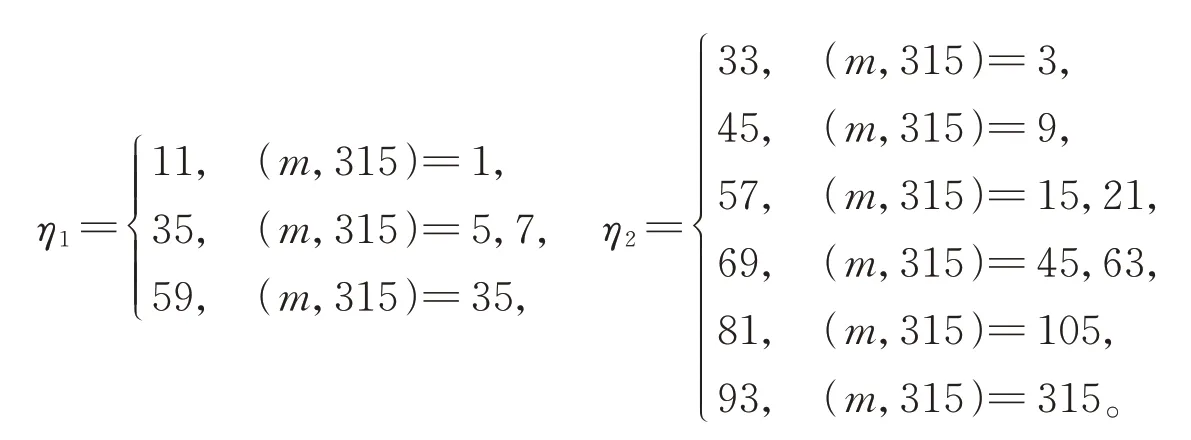
当m为偶数时,则有

其中

证明与引理5 的证明类似,此处略。
引理11设m是正整数。若2|m,则|θ4|=m-1-ϵ,ϵ是γ ∈{6,8,10}时,满足γx≡0(mod m)的互不相同的正整数x∈(0,m)的个数。否则为0。
证明思路类似于引理3,此处略。
引理12设m是正 整数,当8|m时,|θ51|=2;当9|m时,|θ52|=9;当10|m时,|θ53|=17;当11|m时,|θ54|=10;当12|m时,|θ55|=17;否则为0。
证明经过验证,θ5i中的每个代表元X生成的轨道都是互不相交的,因此结论得证。
定理1设m为正整数,当m为偶数时,则有

其中

当m为奇数时,则有
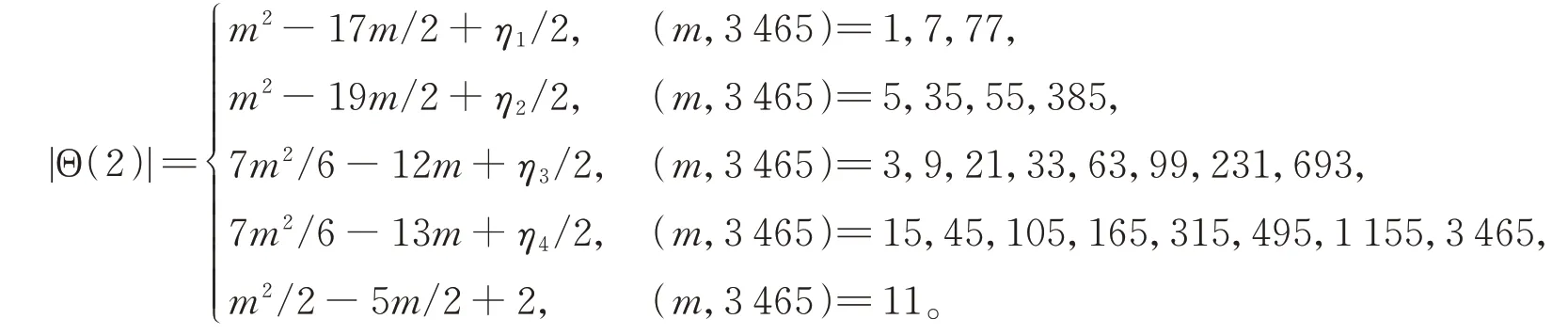
其中
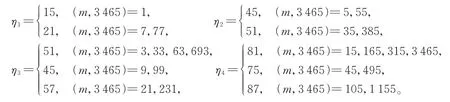
根据引理1 和定理1,以及文献[3]中得出的结果,可以进一步得到Φ(m,5,2,4)的值。
