高维空间上具有时变系数和吸收项的非线性非局部抛物方程解的全局存在性和爆破
2022-06-30欧阳柏平
欧阳柏平
(广州华商学院 数据科学学院,广东 广州 511300)
0 引言
近几十年来,抛物方程和抛物系统解全局存在性和爆破问题的研究取得了丰硕成果。学者们开始考虑的是三维空间中齐次边界条件(Dirichlet 条件和Neumann 条件)和Robin 条件下解的全局存在性和爆破问题[1-6],如在一定条件下解的爆破率、爆破时间的上下界等。之后,又进一步考虑了在高维空间中齐次边界条件下以及非线性边界条件下解的全局存在性、爆破时间的上下界等问题[7-12]。近年来有学者对带有时变或空变系数的抛物方程和抛物系统解的全局性和爆破问题进行了研究[13-17],得到了相关的结论。Chen 等[18-20]考虑了其他偏微分方程解的爆破问题。在应用中,发现非局部项的数学模型比局部项的数学模型更有实际价值,因而探讨非局部项的抛物方程解的全局存在性和爆破现象有较大的理论和实际意义。然而,对于非局部项的数学模型来说,需要重新探索解决其数学模型的理论和方法。因为局部项的数学模型的理论和数学方法不再适用,此课题的研究有较大的困难。文献[21-24]研究了Robin 边界条件、齐次Dirichlet 边界条件以及非线性边界条件下非局部项的抛物方程和抛物系统解的爆破问题。对于解的爆破时间上下界的估计的研究中,考虑和讨论爆破时间上界的方法较多,而对于爆破时间下界的确定则相对有限。
文献[16]研究了如下具有时变因子和吸收项的多孔介质方程爆破问题:
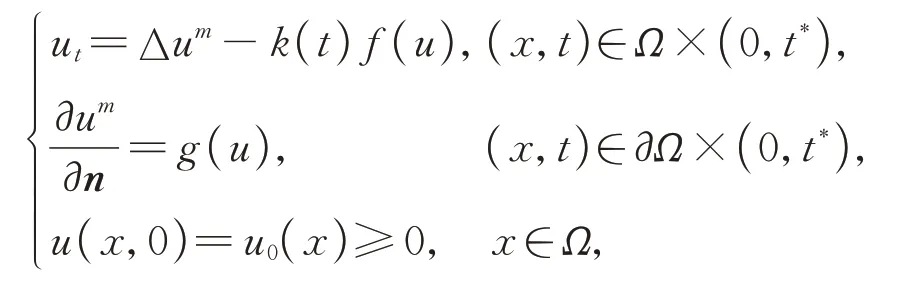
在一定的假设条件下,得到解的全局存在性和爆破发生时解的爆破时间的上界和下界估计。
文献[23]研究了非局部多孔介质方程爆破问题:
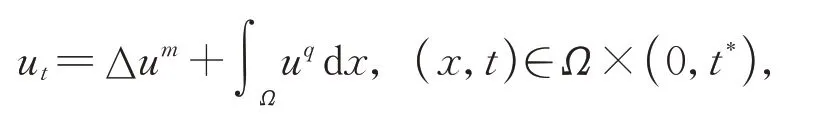
在齐次Dirichlet 和齐次Neumann 边界条件下,得到在R3中爆破发生时解的爆破时间的下界估计。Fang 等[24]研究了具有吸收项的非局部多孔介质方程爆破问题:
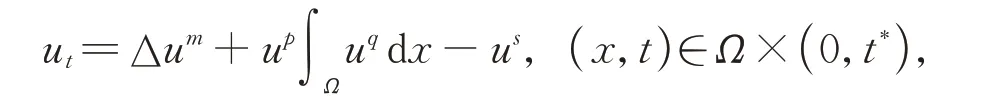
在齐次Dirichlet 和齐次Neumann 边界条件下,得到了在R3中爆破发生时解的爆破时间的下界估计。
受以上文献的启发,本文研究如下高维空间上具有时变系数和吸收项的非线性非局部抛物方程解的全局存在性和爆破:
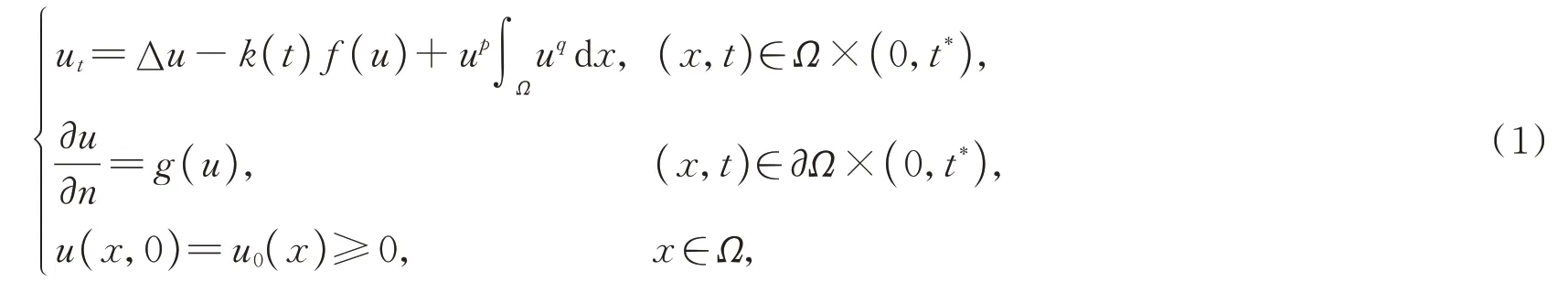
其中:Ω是高维空间Rn(n≥3)中的一个有界凸区域,∆代表拉普拉斯算子;∂Ω是区域Ω的边界;t*代表可能的爆破时间是u在边界∂Ω上的外法向量的导数,假设其足够光滑。
方程(1)在物理学中可以用来描述多孔介质牛顿流的浓度、传热导体温度的扩散等物理现象,在生物种群理论中用于描述生物种群密度等生物现象,有关文献见[25-27]。
目前,关于式(1)高维空间上具有时变系数和吸收项的非线性非局部抛物方程解的全局存在性和爆破问题研究较少,其困难在于如何找到合适的约束条件构造合理的能量函数解决高维上非线性边界条件下时变系数和吸收项对解的全局存在性和爆破影响。本文运用高维空间中的Sobolev 嵌入不等式以及相关的微分不等式得出非线性边界条件下解的全局存在性和爆破发生时解的爆破时间下界估计。
1 全局存在性
引理1[17]设Ω是Rn(n≥3)上的有界凸区域,则对于u∈C1(Ω),n>0,有不等式

引理2[28]Sobo lev 不等式
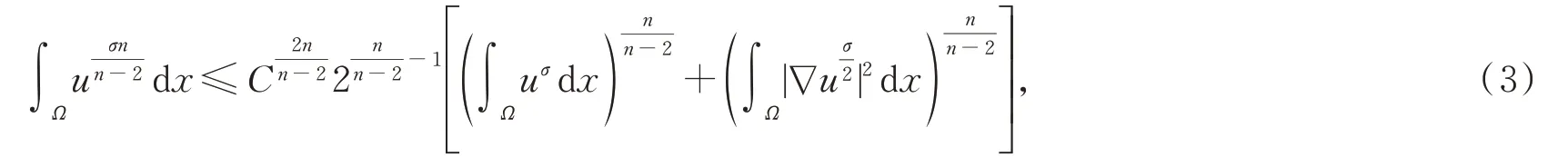
其中C=C(n,Ω)是一个与n和Ω有关的Sobolev 嵌入常数。
定理1假设满足条件
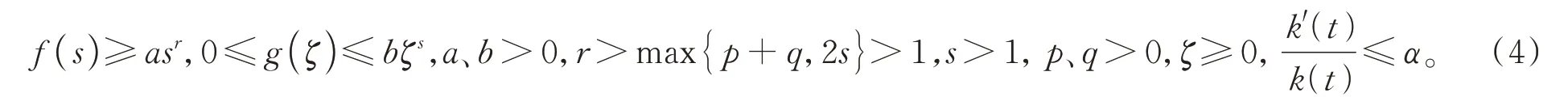
则问题(1)的解在任何有限时间都是有界的,即问题(1)是全局存在的。
证明首先定义辅助函数

其中σ>1。
运用散度定理,首先对式(5)求导数并结合 式(4),得
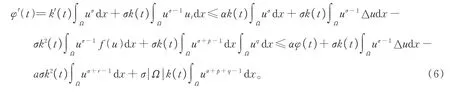
对于式(6)右边第二项,由散度定理和式(2),有
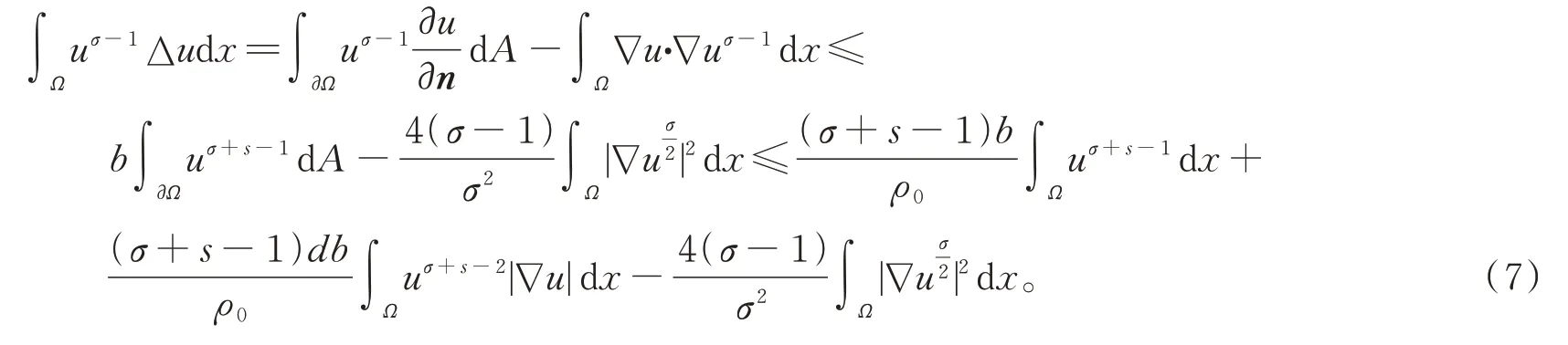
对于式(7)右边第二项,由Hölder 不等式和Young 不等式,得
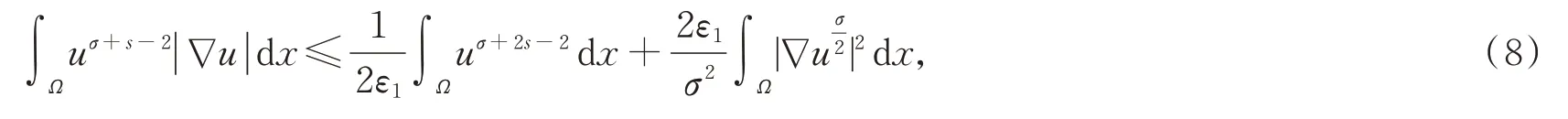
其中ε1是在后面会定义的正数。
于是,由式(7)和式(8),得
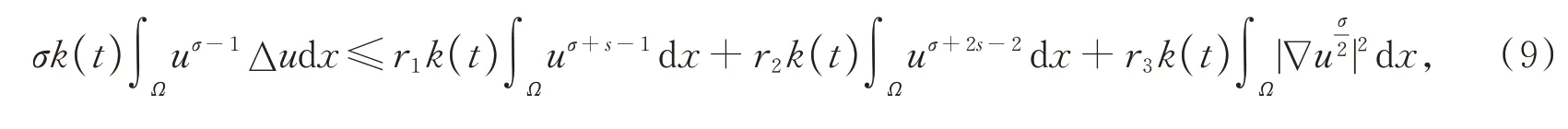
其中
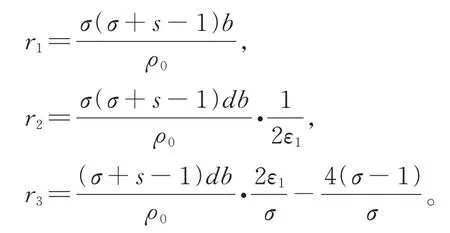
联立式(6)和式(9),有
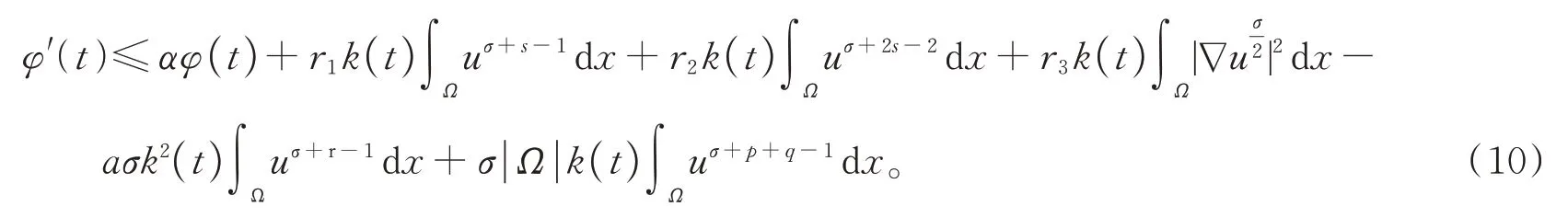
由Hölder 不等式和Young 不等式,得
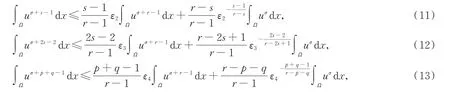
其中ε2,ε3,ε4是在后面会定义的正数。
联立式(10)~(13),有
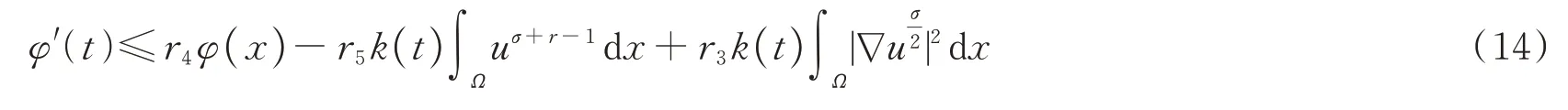
其中
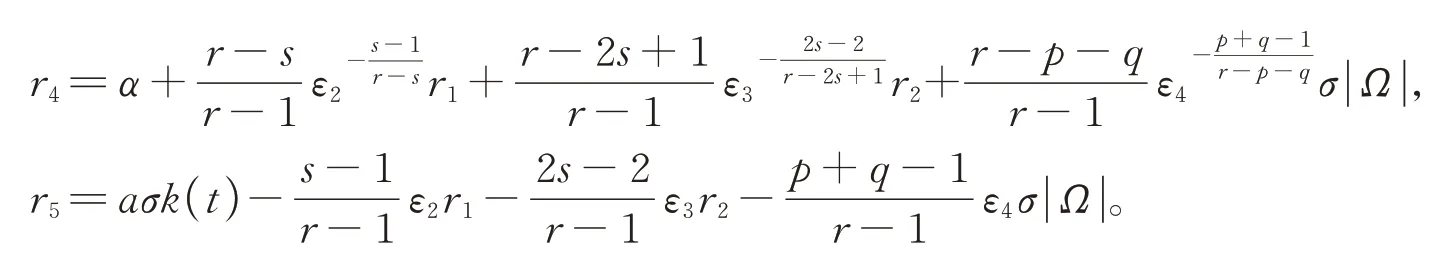
对于r5,可以选取合适的ε2,ε3,ε4,使得r5>0。
由Hölder 不等式,得

结合式(14)~(15),可推出
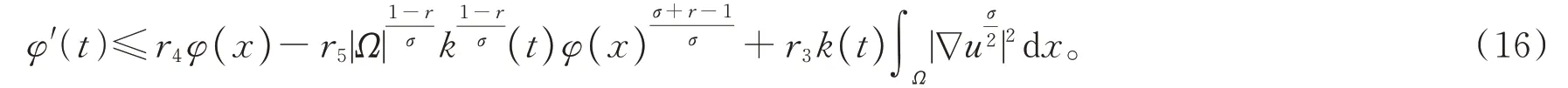
选取合适的ε1使得r3≤0,于是(16)式化为

如果u在φ(t) 度量下在某个t*爆破,即根据式(17),有φ′(t)≤0,∀t 假设满足条件 构造如下辅助函数 其中:σ>n(s-1),δ>1。 定理2假设u(x,t)是问题(1)、(18)在有界凸区域Ω的经典的非负解,则式(19)中定义的能量满足微分不等式 由 此 可 得 爆 破 时 间t*的 下 界 为t*≥Θ-1(S),其 中K1,K3,K5,K6(t),K7(t),ξ1,ξ2,Θ,S均 在 后 面 定 义,Θ-1是Θ的反函数。 证明运用散度定理,首先对式(19)求导数并结合式(18),得 对于式(20)右边第二项,由式(7)和式(8),得 联立式(20)和式(21),有 由Hölder 不等式和Young 不等式,得 联立式(13)、(22)、(23),可知 其中 选取合适的ε4,使得K2≤0。于是,式(24)化为 对于式(25)右边第二项,由Hölder 不等式和式(3),可得 其中 ε5为后面会定义的常数。 由式(25)、(26)得 其中 选取合适的ε1、ε5使得于是式(27)化为 其中 因为ξi>1(i=1,2),所以式(29)右边积分存在。显然,Θ(t*) 是单调递增函数,于是有 其中Θ-1是Θ的反函数。 从而定理2 得证。 本文通过Soblev 不等式和其他微分不等式方法研究了高维空间上具有时变系数和吸收项的一类非线性非局部抛物方程在非线性边界条件下解的爆破问题,并得到了解的全局性和爆破发生时解的爆破时间的下界估计,进一步丰富了有关高维空间上非线性非局部抛物方程解的全局性和爆破研究。2 爆破时间的下界
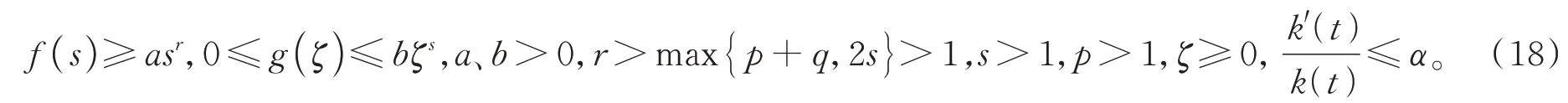

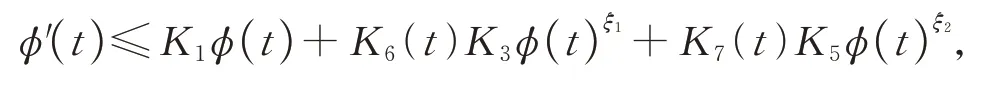
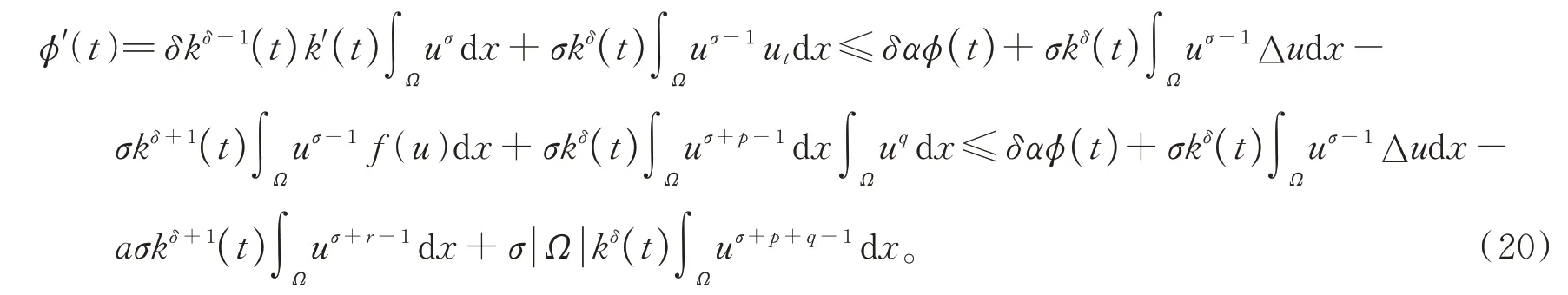
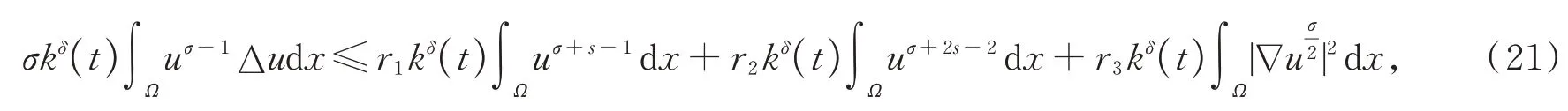
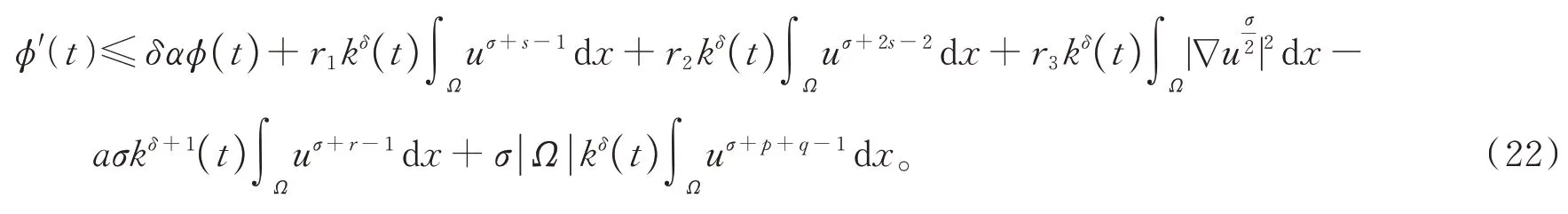
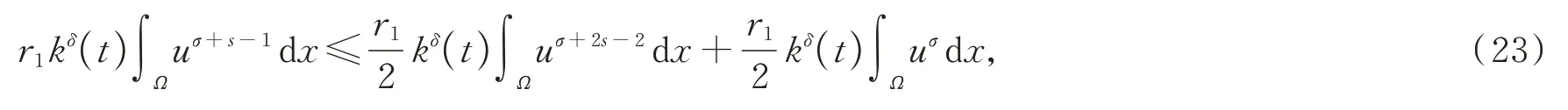
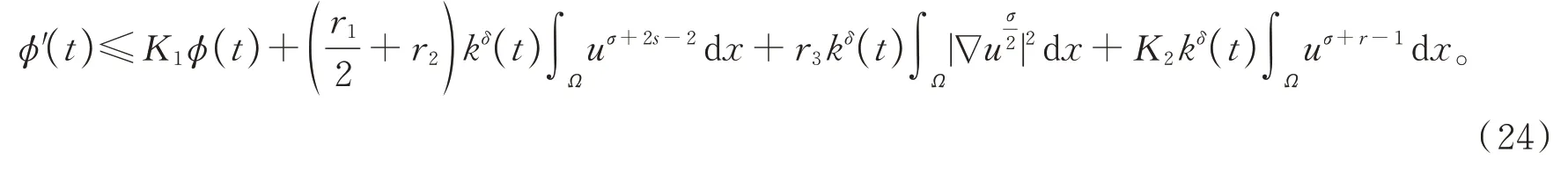
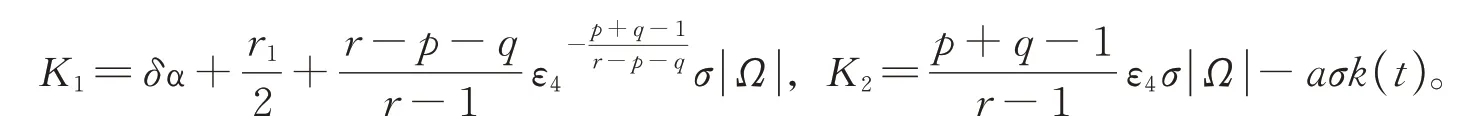
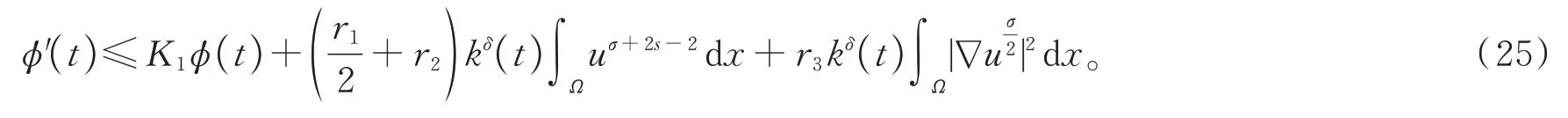
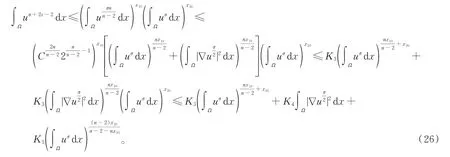
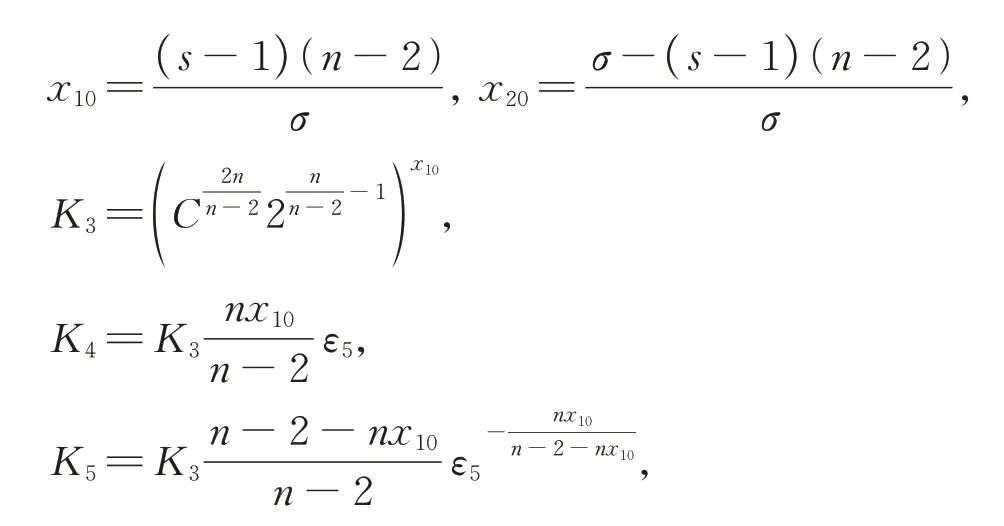
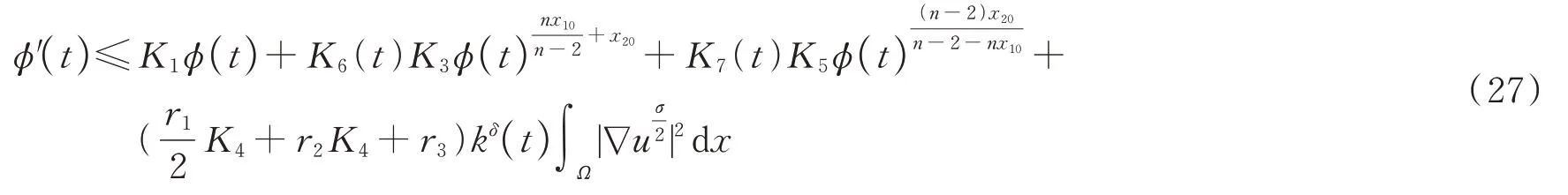
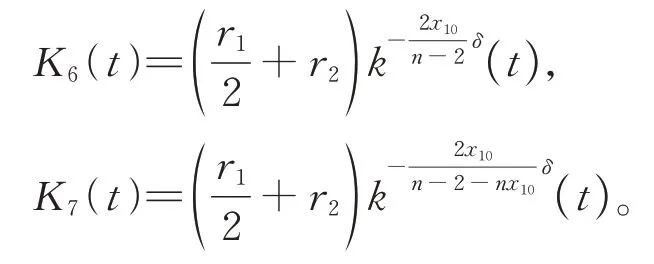
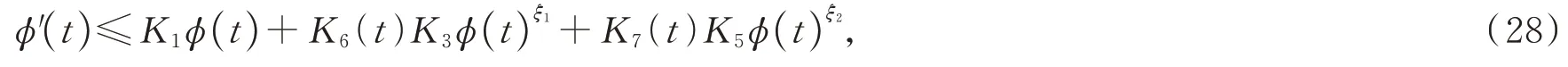
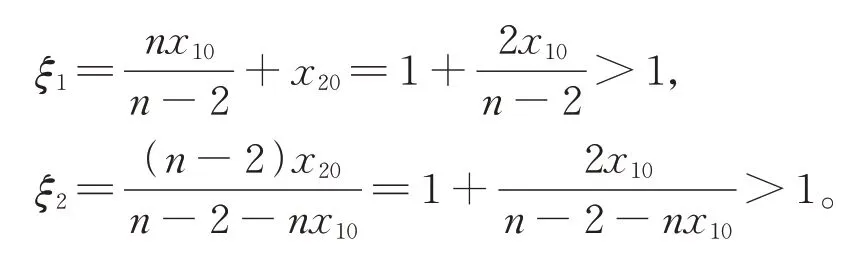


3 结语
