静力触探技术(CPT)在砂性地基处理验收检测中的应用
2022-06-30郭嫣嫣
张 林,郭嫣嫣
(大连理工大学土木建筑设计研究院有限公司,辽宁 大连 116023)
国外某项目直立式防波堤属于深水防波堤,原始水深在30~40 m,根据地勘资料,表层细砂及底层中砂均为易液化砂层,岩层埋深较深。在进行地基处理设计时,若考虑将液化土层全部挖除,则造价高、工期长;而无填料振冲密实法对于砂土地基来说是一种非常有效的地基处理方法。无填料振冲密实法对砂土细颗粒含量较为敏感,理想的情况下,土层细颗粒(粒径<0.075 mm)含量应该小于10%。国内外学者普遍认为振冲挤密法仅适合细颗粒含量小于12%(需要根据土的颗粒级配、振冲器功率、振冲间距等进行试验确定)的粗砂或者中细砂地基[1]。该项目原状土层细颗粒含量分布范围较广,在9%~25%。为了达到预期的处理效果,首先根据Brown提出的方法[2]利用土的颗粒级配判别砂土是否适合振冲,然后将不适合振冲的、含泥量过大的细砂挖除后对底层中砂进行无填料振冲密实。
为了保证砂土不液化、满足结构安全及使用要求,国外工程师提出了以下振冲验收标准:液化判别安全系数大于1.25、砂土的相对密度大于70%、有效内摩擦角大于35°、地基承载力大于300 kPa、20 a工后沉降小于30 mm。
针对砂土的相对密度和有效内摩擦角等参数的确定,本文对比分析国内外常用的基于静力触探CPT的计算公式,分析各公式的适用范围,结合工后沉降量确定验收曲线。最后,根据CPT验收曲线计算承载力和液化判别,可为相似工程验收提供参考。基于CPT的液化判别可参考Boulanger方法[3]。
1 相对密度
砂土的相对密度作为力学特性的指标广泛应用于工程中,判断砂土的密实状态的最简便方法是利用孔隙比。孔隙比不能反映土颗粒的形状和级配,对于不同的砂土,相同的孔隙比不能说明密实度也相同[4]。因此,引用相对密度Dr来评价土的密实状态。
(1)
式中:e、emax、emin分别为原始、最大、最小孔隙比。
孔隙比的测定往往伴随一定的误差,此外,粗粒土的应力、应变和强度特性过于复杂,不能仅用土的相对密度来表示。然而,国外一些项目仍然会使用相对密度作为经过地基处理土层的验收标准,所以相对密度仍然应用广泛。
由于从砂土中提取未扰动样本十分困难,且成本较高。工程上常用原位试验数据建立与相对密度的相关性,得到经验公式,这种间接的评估方法增加了诸多不确定性。通过与在实验室中确定的相对密度比较进行数据校正,原位试验方法已被广泛应用于岩土工程。
静力触探(CPT)在确定土的类型、变形特性、强度特性和渗流固结方面均有十分广泛的应用、成果准确可靠。Schmertmann[5]在实验室进行CPT试验,首次提出了锥尖阻力qc和相对密度Dr之间的综合关系。并认为对于正常固结、未老化的细至中砂(细颗粒含量小于5%),相对密度Dr由下式计算:
(2)

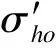
Jamiolkowski[7]提出了归一化锥尖阻力Qcn(基于qc计算)与相对密度Dr的公式。
(3)
(4)

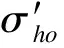
为了简化计算,对于砂土,Robertson[9]将公式(4)中C1用0.5代替,最终得到公式(5)。然后代入公式(3)中计算相对密度。同时Robertson提出公式(5)计算的Qcn可以用公式(6)计算的Qtn代替。对于砂土,计算所得Qcn比Qtn高约3%,对相对密度Dr的计算基本没有影响。
(5)
(6)
式中:Qtn为归一化锥尖阻力(基于qt计算);σvo为总竖向应力;qt为经孔压u2修正的锥尖阻力,qt=qc+u2(1-a);u2为锥肩部位测试的孔隙水压力;a为圆锥头锥底的横截面积与圆锥头顶柱的横截面积之比;n为随土壤类型而变化的指数,对黏性土,n=1;对纯净砂,n=0.5;对粉土和砂质粉土,n在0.5~1取值。
Lunne等[10]建议只在测量了u2的情况下进行孔压修正。否则,在砂土中,可以近似用qc代替qt。面积比a在0.7~0.9变化,其取值不能仅从几何因素来确定,而应通过实验室校正或类似的试验来确定。

表1 不同研究者定义的C0、C1、C2常数
Kulhawy和Mayne[11]提出了一种更简单的估算相对密度的公式:
(7)
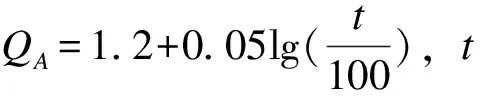
对于大多数年代近的、未胶结的硅基砂,公式(7)可以简化为:
(8)
公式(8)中的常数350通常对应于中砂;对于细砂,该常数可以接近300;对于粗砂,该常数可以接近400。
国内规范《水运工程静力触探技术规程》[12]无黏性土相对密度计算公式如下:
Dr=(31.78lnqt-13.98)/100
(9)
国内规范的计算公式是通过室内试验及现场内置环刀取砂器得到的干密度计算相对密度,然后与对应的CPTU数据分析得出公式(9),在给定验收相对密度后,qt不随深度改变。
Schmertmann、Jamiolkowski、Baldi、Robertson根据大量试验结果,提出的公式(2)(3)不仅考虑了锥尖阻力与相对密度的关系,还考虑了有效垂直应力对其的影响。Kulhawy和Mayne方法同时考虑了土的压缩性、老化因素、超固结系数,更为全面。见图1。
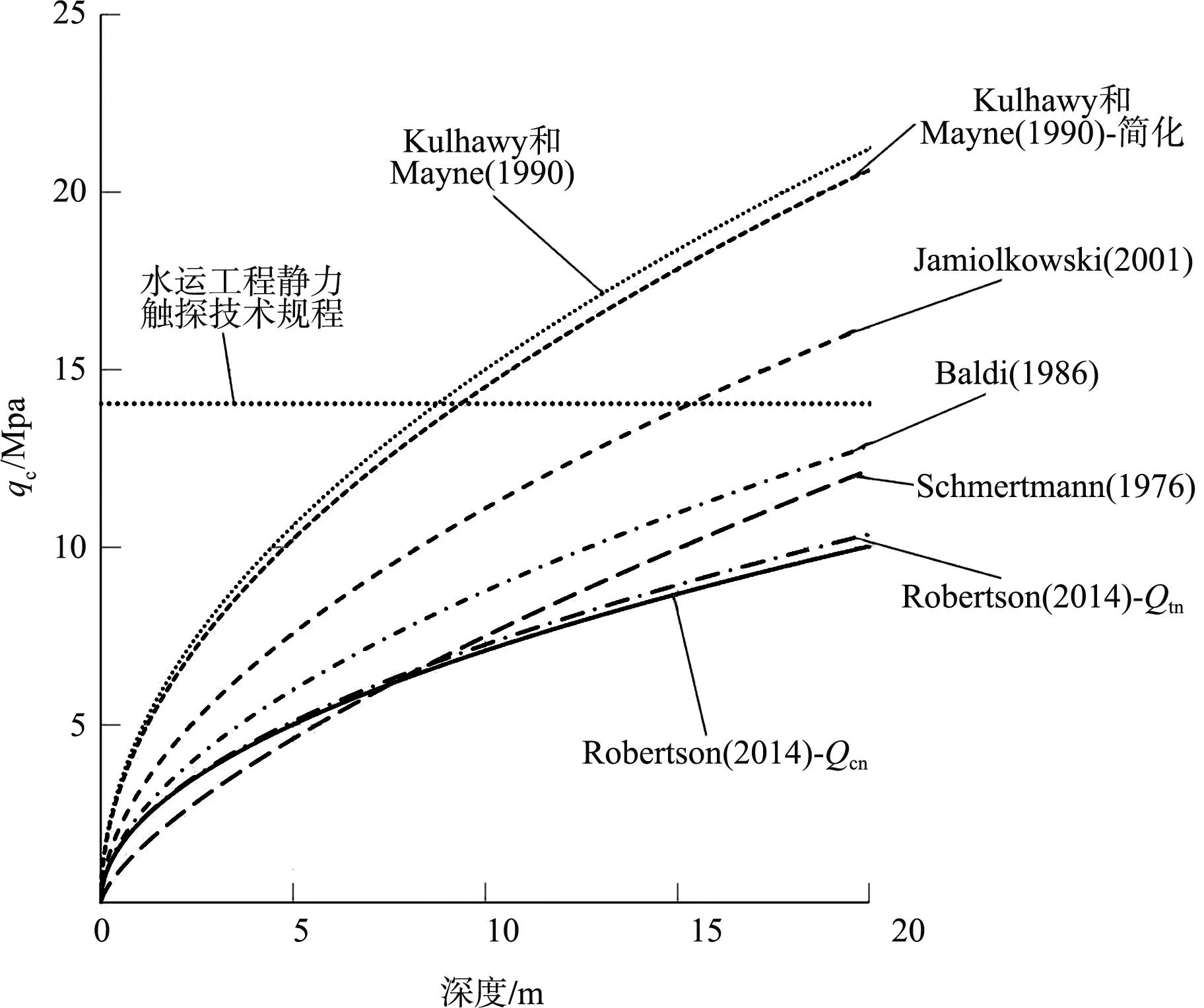
图1 不同方法基于相对密度要求的CPT验收曲线
相对密度作为振冲密实法验收指标,取值在70%~90%。一般以相对密度达到70%为基准[13]。本项目亦采用70%的标准,国外项目例如塞内加尔达喀尔港、阿什杜德港,也使上述标准作为验收条件。但因每个项目的地质情况不同、设计条件不同,相对密度达到70%作为一项验收指标,应结合地质条件、设计条件综合确定。
为了达到Dr=70%的验收标准,进行无填料振冲密实后的地基应满足基于CPT的最小qc值。国外方法达到Dr=70%时,不同深度需要的qc值不同,土层越深qc值越大。Kulhawy和Mayne及简化方法计算的qc值最大,其简化方法公式(8)中参数取值范围大,需要一定的工程经验,所以应用上具有局限性;Jamiolkowski的计算结果接近平均值;Schmertmann、Baldi计算值稍大;Robertson计算值最小。本文为了对比有效内摩擦角、承载力、沉降等验收指标与相对密度的控制关系,首先采用Robertson方法确定相对密度验收曲线。若有效内摩擦角、承载力、沉降等验收指标控制验收标准,应采用图1中其它方法提高验收标准或者对Robertson方法进行局部修正。
2 状态参数
虽然土体的相对密度被广泛用于表征砂土液化地基或吹填工程等的密实度。砂土的变形特性主要取决于土体相对密度与所处的有效应力水平[14]。Been和Jefferies为了同时反映相对密度与应力水平变化对砂土变形性质的双重影响,提出了状态参数ψ的概念,见图2,即在相同平均有效应力下,砂土的孔隙率e与临界状态孔隙率ec之差。当ψ>0表示砂土当前处于松散状态,在荷载作用下发生剪缩;当ψ<0表示砂土当前处于密实状态,受荷作用下发生剪胀。
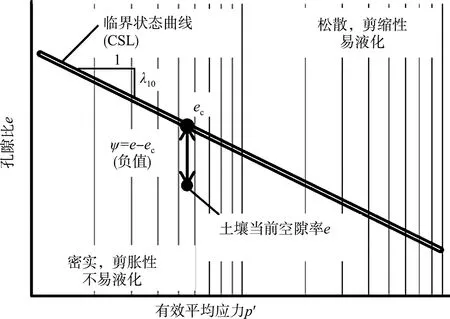
图2 状态参数定义
Been和Jefferies[15]提出了利用CPTU确定状态参数的方法:
(10)
(11)
m=11.9-13.3λ10
(12)
(13)
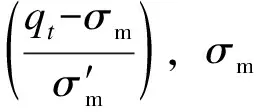
Plewes等[16]建议用以下方法来估算λ10:
(14)
式中:F为归一化摩阻比,F=fs/(qc-σvo),fs为侧壁摩阻力。
Robertson[17]基于Been 和Jefferies提出ψ与Qtn,cs之间的简化近似关系:
ψ=0.56-0.33lgQtn,cs
(15)
Qtn,cs=KcQtn
(16)

Robertson在基于CPT土壤分类图上近似地绘制出状态参数等值线,见图3。Robertson认为在利用CPT计算状态参数的实际应用中,收缩-膨胀的边界在经验上应被取为ψ=-0.05。

注:1.灵敏细粒土;2.有机土壤-泥炭;3.黏土:粉质黏土-黏土;4.粉土混合物:黏质粉土-粉质黏土;5.砂混合物:粉砂-砂质粉土;6.砂:纯净砂-粉砂;7.砾砂-密实砂;8.非常硬的砂-黏土砂;9.极硬细砂。
当砂土(Ic≤2.05)相对密度达到70%时(利用Robertson计算锥尖阻力,下同),ψ=-0.12~-0.08,砂土当前处于密实状态;相对密度达到90%时,ψ=-0.19~-0.15。综合上述相对密度和状态参数指标,经过振冲处理后的砂土要达到密实状态,70%的相对密度验收标准是合理的,且具有经济性。
3 有效内摩擦角
为了保证结构稳定性满足规范要求,在进行上部结构设计时,还需要确定地基砂土的物理力学指标,尤其是砂土内摩擦角。同时,砂土的地基承载力主要由土层的内摩擦角决定[18]。
砂土的抗剪强度通常用有效内摩擦角φ′表示。Robertson提出了公式(17),用于估算未胶结、未老化、适度可压缩、主要为石英砂的有效内摩擦角φ′,该公式是基于校准实验室测试的结果。
(17)
Kulhawy和Mayne提出适用于磨圆度好的非胶结石英砂有效内摩擦角评估经验公式:
φ′=17.6+11lgQtn
(18)
公式(17)(18)所得的砂土内摩擦角全部大于试验结果,很大程度上高估了砂土内摩擦角[19]。因此,该式在计算混有细粒质砂土时应根据区域经验进行折减。对于细粒土,确定有效内摩擦角的最佳方法是通过高质量原状土的固结三轴试验。
Jefferies和Been[20]研究表明,对于大部分砂土,状态参数ψ与峰值摩擦角φ′之间存在很好的相关性。
(19)

国内规范JTS/T 242—2020《水运工程静力触探技术规程》无黏性土的有效内摩擦角计算公式如下:
粉砂、细砂:
φ′=3.65ln(qt-σvo)+27.1
(20)
中砂、粗砂、砾砂:
φ′=3.30ln(qt-σvo)+29.5
(21)
Jefferies和Been基于状态参数的公式计算值偏大,但与其他方法相比更具有优势,因为状态参数包括了土层颗粒特征和矿物学的重要性。
Robertson计算有效内摩擦角的公式与Jefferies和Been结果相差不大,见图4。与国外公式相比,国内规范相同深度的土层摩擦角整体偏小,因此需要的qc最大。当砂土相对密度达到70%(Robertson)时,根据相同深度对应qc计算的有效内摩擦角,上述4种方法计算的值在36.7°~42.3°,均满足验收标准。
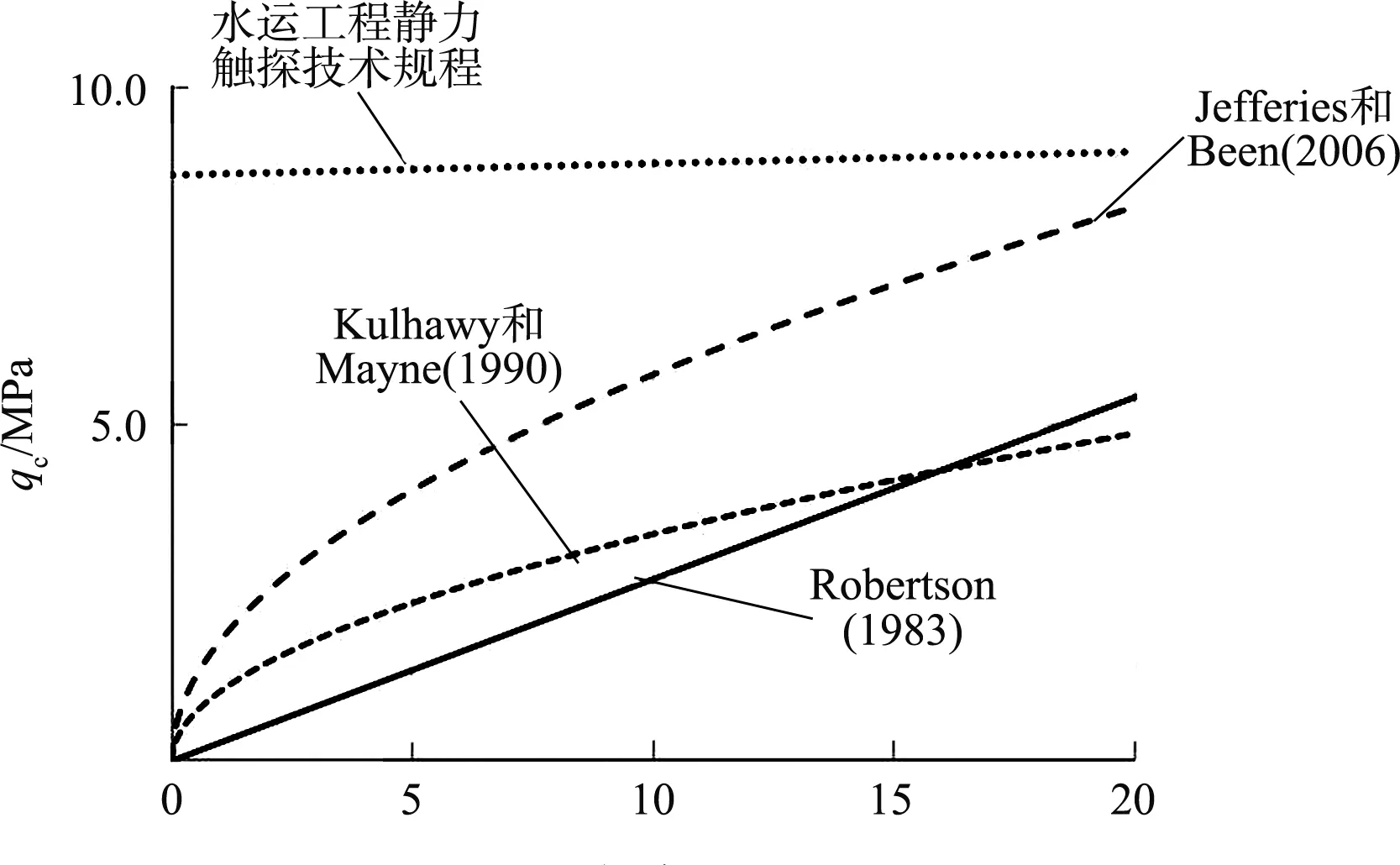
图4 不同方法基于有效内摩擦角要求的CPT验收曲线
4 沉降及承载力
在砂土基础设计中,既要满足稳定性的要求,又要满足沉降量要求。砂土渗透性高,因此沉降会立即发生。然而,由于外界因素如水位变化、地震荷载等,工后沉降也不可忽视。砂土的工后沉降主要由土体蠕变产生。
Schmertmann[22]提出了一种计算砂土地基沉降的方法,即将地基下的土壤划分成不同的层,然后计算每一层的沉降,各层的沉降之和表示土体的总沉降。该方法是计算颗粒土地基沉降最合理的方法之一,在世界范围内得到广泛应用。
(22)
Ei=αEqc
(23)
αE=0.015(100.55Ic+1.68)
(24)
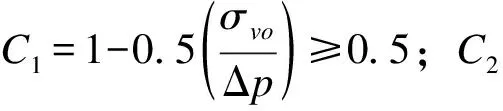
Ei除利用公式(24)计算以外,对于年轻正常固结砂,可取2qc~4qc;对于年代大于1 000 a的正常固结砂,可取4qc~10qc;对于超固结砂可取6qc~20qc。
Schmertmann方法基于大量工程实例进行计算,计算公式简单、物理意义明确。研究表明,Schmertmann方法计算所得的沉降值与实测值相差不大,其影响沉降量计算精度的关键是确定杨氏模量。经计算,在达到70%(Robertson)的相对密度情况下,附加应力为300 kPa的条形基础工后沉降为32.8 mm,大于设计要求的30.0 mm;相对密度达到80%时,为25.8 mm;相对密度达到90%时,为20.3 mm。
根据相对密度等于70%确定的CPT验收曲线,利用国外方法计算的表层砂土锥尖阻力较小,因此计算的工后沉降主要发生在表层。为了工后沉降满足要求,应对Robertson验收曲线进行修正,使表层锥尖阻力大于6 MPa,见图5。计算所得沉降量为29.3 mm。或者直接采用Baldi确定验收曲线,计算沉降量为26.5 mm。两种方法确定的验收曲线均是相对经济的,初步确定工艺参数后,需经过试验区验证其适用性方可进行大规模振冲处理。必要时应该分区确定验收曲线,以确保工程质量。
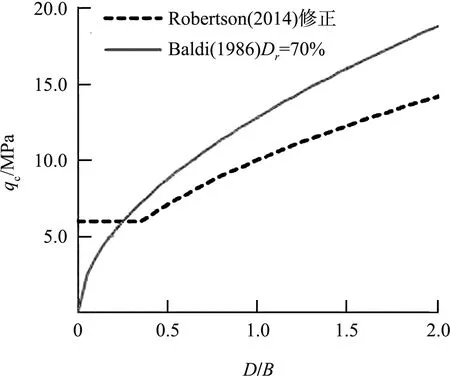
注:D为深度;B为宽度。
按照上述验收曲线进行地基处理后,计算深度范围内锥尖阻力qc(av)>7.0 MPa。根据Robertson提供的承载力计算公式,容许承载力qall>370 kPa,满足验收标准。
5 结论
1)为了达到地基处理预期的效果,首先应判别砂土是否适合振冲。国内外普遍认为振冲挤密法仅适合细颗粒含量小于12%~15%的粗砂或者中细砂地基,Brown利用土的颗粒级配判别砂土是否适合振冲,具有一定参考意义。
2)综合相对密度和状态参数指标,经过振冲处理后的砂土(Ic≤2.05)相对密度达到70%时,状态参数ψ小于临界值(Robertson建议取-0.05),砂土处于密实状态。从压实效果方面考虑,70%的相对密度验收标准是合理的,且具有经济性。
3)Jefferies和Been基于状态参数的计算有效内摩擦角的公式,计算φ′偏小,约为37°,但与其他方法相比更具有优势,因为状态参数包括了土层颗粒特征和矿物学的重要性。
4)根据相对密度为70%确定的CPT验收曲线,利用国外方法计算的表层砂土锥尖阻力较小,计算的工后沉降较大(附加应力为300 kPa的条形基础,沉降大于30 mm)且主要发生在表层。因此适当提高表层砂土的锥尖阻力以达到设计要求,相比于提高相对密度至80%,更具有经济性。
5)根据最终验收曲线,利用Robertson提供的承载力计算公式,容许承载力qall大于300 kPa;利用基于CPT液化判别的Boulanger方法,在矩震级为7级,地震动峰值加速度0.1g的场地,液化判别安全系数大于1.25,均满足设计要求。
