坡度变化率建模的低分辨率坡度补偿方法

尹 力，叶乐佳，邸凯昌，刘 斌，孙小珠，王长焕，薄 正

（1.中国科学院 空天信息创新研究院 遥感科学国家重点实验室，北京 100101；2.中国科学院大学，北京 100049；3.中国科学院 比较行星学卓越创新中心，合肥 230026；4.上海宇航系统工程研究所，上海 201109）

引 言

地表坡度作为一项重要的地形参数，在深空探测中广泛应用于地形地貌分析[1]、路径规划[2-3]、着陆点选择[4-5]等科研和工程任务中。坡度图一般由数字高程模型（Digital Elevation Model，DEM）提取得到，因此，坡度图的分辨率和精度受到DEM的限制[6]。各种科研或工程任务均对高质量坡度数据提出了需求，特别是在着陆器和行星车任务中，如着陆点地形特征分析、行星车导航规划等方面都需要高分辨率大范围的坡度图。然而，DEM通常由立体影像或激光高度计数据生成，以月球和火星为例，激光高度计采样间隔较大，通常为百米量级，高分辨率立体影像则仅在月球和火星少数区域存在[7-8]，导致全球覆盖的月球和火星DEM都是低分辨率的（格网间距几十到上百m），高分辨率（米级格网间距）DEM产品仅在局部小范围内可用[9-10]。低分辨率DEM生成的坡度相对平滑，也就是说，在同一区域内，低分辨率DEM生成的坡度要低于高分辨率DEM生成的坡度,即出现了坡度低估现象[11]。因此，现有DEM数据生成的坡度产品，往往难以满足应用要求，尤其是行星着陆探测器可达性分析和巡视导航设计的安全要求。

针对坡度转换及坡度低估问题，国内外学者做了众多研究及探索，研究场景包括地球以及行星。汤国安等[12]分析了在不同地形复杂度条件下DEM的不确定性，建立了多尺度的地形分析模型以及尺度转换模型。王英等[13]以30 mDEM为基础，利用分形结合半方差函数的方法分析低分辨率DEM提取的坡度与高分辨率DEM提取的坡度之间的转换规律。Zhang等[14]用分形理论，通过变异函数法定义可提供坡度与空间分辨率之间的关系信息的分形参数，并讨论了分形参数在不同尺度上的变化，建立了一种低分辨率坡度补偿的模型。以西班牙南部不同分辨率的DEM对该模型进行验证，结果表明该方法相对于直接从低分辨率DEM导出的坡度在准确性方面有了显著提升。陈燕等[15]通过坡度转换图谱的方式，选择黄土高原典型地貌类型的试验区域，对该区域低分辨率DEM提取出的坡度统计值进行误差纠正。

针对行星也有相关的坡度补偿工作，Wang等[16]以HiRISE影像作为试验数据，提出了一种应用于火星坡度纠正的模型，实验表明该模型可应用于不同分辨率差异的场景中。Wu等[17]还利用该模型所提出的坡度补偿方法对月球上的低分辨率坡度图进行了补偿及分析，验证了该方法应用于行星场景的可行性与有效性。

分析发现，该补偿方法在坡度突变区域表现欠佳，大误差普遍聚集在坡度突变处。本文提出一种改进的低分辨率坡度补偿模型，利用拉普拉斯算子提取的待补偿坡度的变化率信息作为自变量加入补偿函数中，从而提升坡度补偿精度。选取覆盖多种地形的月球和火星数据进行实验及误差分析，并与传统方法做出对比，验证本文提出方法的有效性与适用性。基于本文提出的方法开展应用研究，拟合生成了适用于全月的补偿模型，另有坡度分级补偿模型作为全月补偿模型的补充；对覆盖“天问一号”的“祝融号”火星车着陆点50 km×50 km范围内的低分辨率坡度进行补偿。

1 引入坡度变化率的补偿方法

本文提出的低分辨率坡度补偿方法流程如图1所示。首先，选取覆盖同一区域的高分辨率DEM（如LROC NAC DEM、HiRISE DEM）和低分辨率DEM（如HRSC-MOLA融合DEM）。从高分辨率DEM中提取高分辨率坡度作为目标值，从低分辨率DEM中提取低分辨率坡度作为待补偿值。此外，为了与低分辨率坡度图逐像素对应，需要对高分辨率坡度进行降采样，即找到同一低分辨率坡度值与多个高分辨率坡度值之间的对应关系。然后，使用拉普拉斯算子对需要补偿的低分辨率坡度图进行坡度变化率的计算。最后，拟合目标坡度值与待补偿坡度值以及坡度变化率之间的二元线性回归函数。

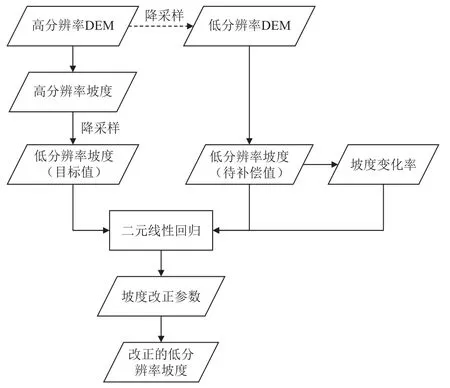
图1 所提出坡度补偿方法的流程图Fig.1 Flowchart of the proposed slope compensation method

1.1 坡度预处理

设地面上某点在x方向上的高程变化率为fx，在y方向上的变化率为fy，则该地面点坡度为β ，β的计算如式（1）所示

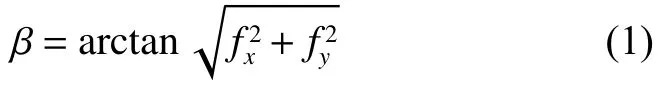
不同的坡度提取方法主要体现在fx与fy的计算方式不同，本文采用三阶反距离平方权差分（Horn算法）[18]，其计算方法为

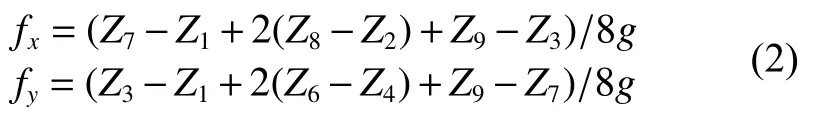
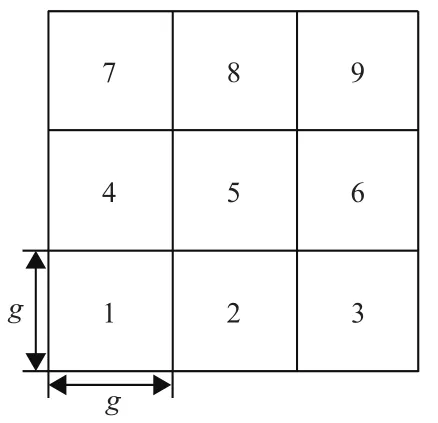
图2 坡度计算方法示意图Fig.2 Slope calculation method

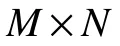
1.2 补偿模型

文献[16]所采用的补偿函数如式（3）所示

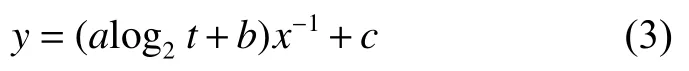
其中：x为待补偿坡度值；y为坡度放大倍数；t为高分、低分DEM分辨率比值；a,b,c均为拟合参数。在DEM分辨率比值一定的情况下，即式（3）中的t值为常量时，可写成

为了更简洁清晰地表示初始坡度与目标坡度之间的关系，可将式（4）的等号左右同时乘x，将方程转化为式（5）的表达形式，本质上是一个一元线性函数

其中：Z为补偿后的低分辨率坡度值；X表示待补偿的低分辨率坡度值；a,b表示线性拟合公式中的参数，其中a为斜率，b为截距。

在该模型中，补偿后的坡度只与待补偿的坡度线性相关，即默认对应的坡度会随着DEM分辨率的降低而线性减小。然而，行星表面有一些重要的地形特征，如撞击坑等，这类地形起伏变化很大，坡度值很大。随着DEM分辨率的降低，发生坡度的突变。此时仍使用一元线性补偿模型，无法还原原始地形。通过分析文献[16]中的补偿结果，发现利用线性补偿后的结果与目标值相减，其残差与补偿前坡度的变化率相关。基于上述分析，本文提出在已有线性补偿函数中加入坡度变化率项。记为X′，作为一个自变量引入到补偿模型中参与拟合。所提模型数学表达式如式（6）所示

其中：Z为补偿后的低分辨率坡度值；X表示待补偿的低分辨率坡度图；X′表示待补偿坡度的变化率；a,b,c表示拟合参数，可基于最小二乘原理拟合得到。

本文中，坡度的变化率用拉普拉斯算子提取获得，拉普拉斯算子具备各向同性，即旋转不变性的性质，并具有计算简单等优势[20]。定义二维坡度图像f(x,y)的拉普拉斯算子为

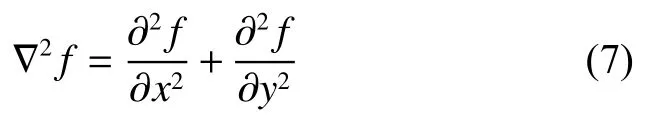
图像是由离散像素组成的，其离散形式为

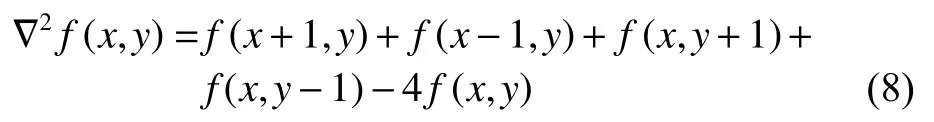
上述公式的右边实际上是坡度图像某像素和它周围的8个像素与图3所示的模板的乘积。模板左上角的像素坐标为(x−1,y−1)，右下角的像素坐标为(x+1,y+1)。如果使用这个模板滑过图像并计算每个像素的拉普拉斯算子，这个过程就是使用拉普拉斯算子计算坡度图像的边缘信息。

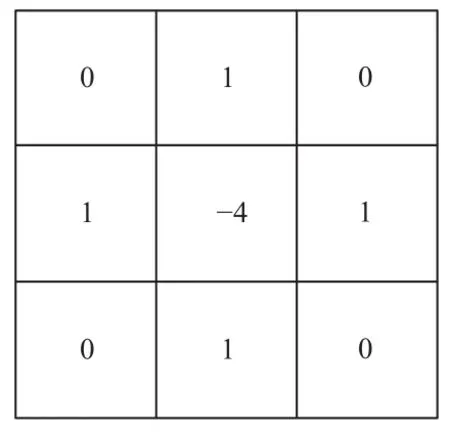
图3 拉普拉斯算计卷积模板Fig.3 Laplacian convolution template

2 实验验证

2.1 实验区域与数据

针对月球实验，选择了全月范围内的14个高分辨率LROC NAC DEM产品，可在华盛顿大学（University of Washington）的PDS Geosciences Node网站（https://ode.rsl.wustl.edu/moon/indexProductSearch.aspx）下载得到。从14个DEM中提取的14幅坡度图及其对应的地形类型和编号如图4所示，它们分布在整个月球表面，地形特征包括高地、月海、撞击坑、盆地和过渡带等。直接下载的DEM的原始分辨率从2、3到5 m不等，本实验为了统一分析方便，首先将下载的原始数据均重采样为5 m。

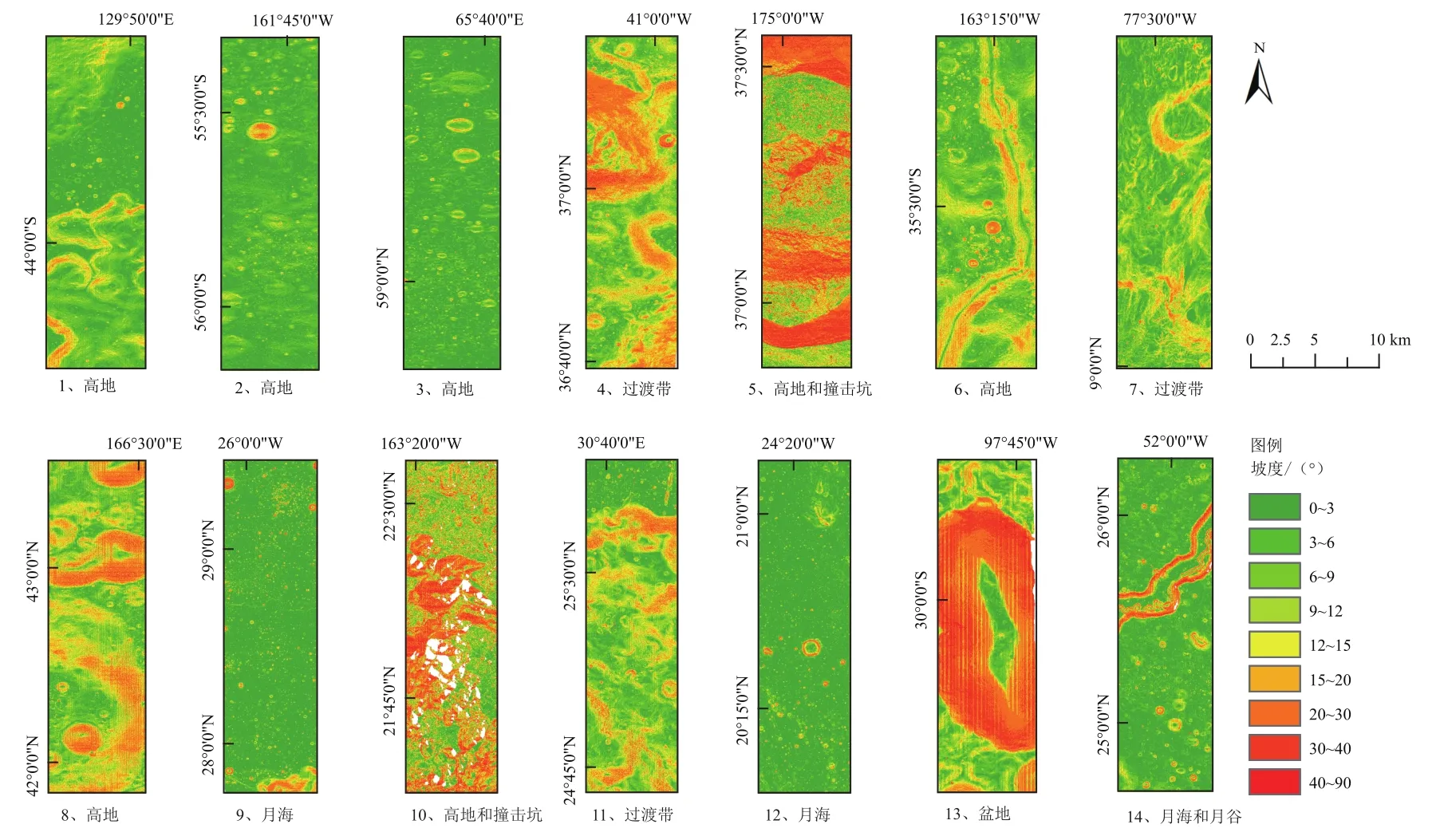
图4 月球坡度实验数据Fig.4 Experimental data of lunar slope

针对火星实验，选取了中国2020年发射的“天问一号”火星任务搭载的“祝融号”火星车着陆区乌托邦平原的6幅1 m分辨率的HiRISE DEM数据，可从亚利桑那大学（University of Arizona）的月球与行星实验室网站（https://www.uahirise.org/dtm/）下载得到。这6个区域的地形非常接近，提取的坡度见图5。

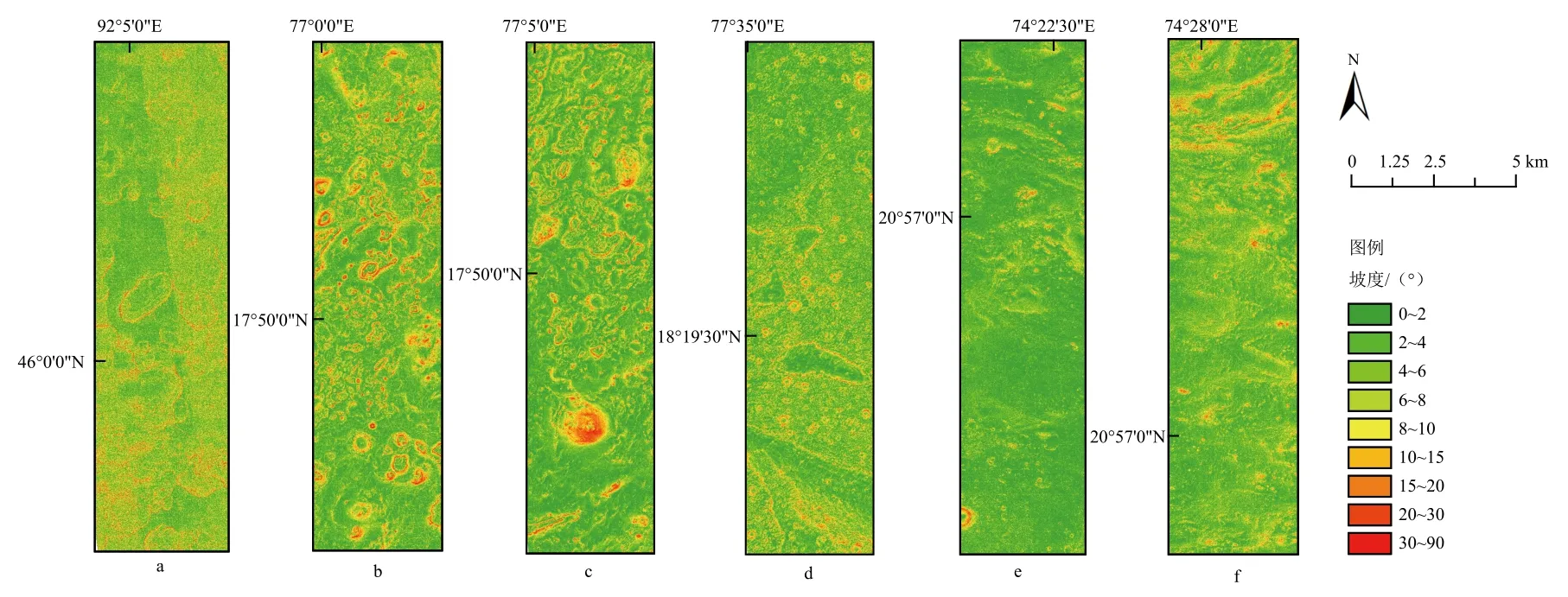
图5 火星坡度实验数据Fig.5 Experimental data of Martian slope

2.2 实验结果与分析

对于同一区域，随着DEM分辨率的降低，坡度低估现象逐渐明显，图6展示了上述月球区域5的一个示例。在图6第1行中，将2 m分辨率的LROC NAC DEM依次降采样至20、100和200 m，在第2行，展示了从这些DEM提取出的坡度图。可以看出，随着DEM的降采样，坡度出现了明显的减小趋势。

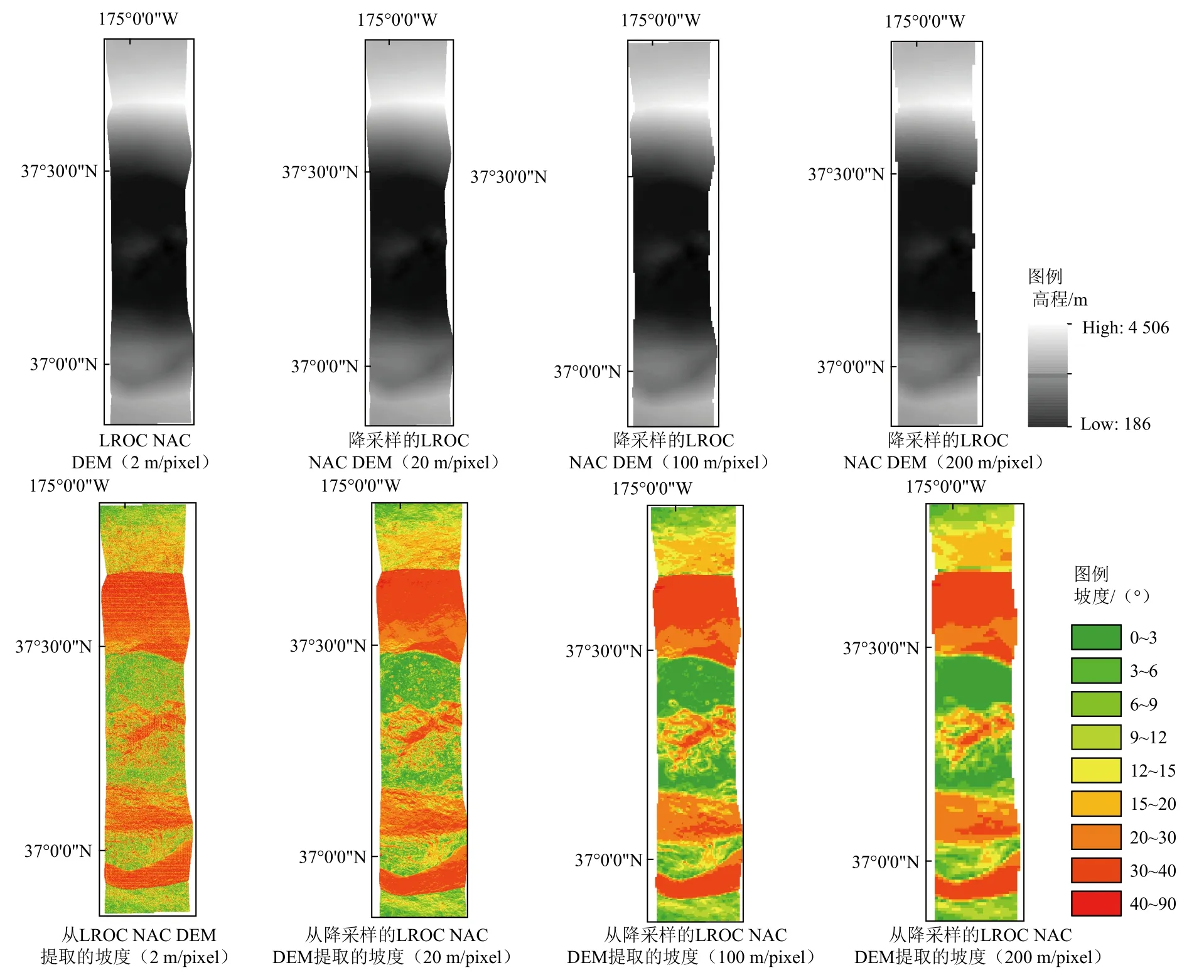
图6 坡度低估现象Fig.6 Phenomenon of slope reduction

为了证明所提出的考虑坡度变化率的补偿方法的效果比传统线性方法有所提高，分别采用式（5）中的线性补偿方法和式（6）中考虑坡度变化率的方法对14个月球区域的坡度数据进行参数拟合，每组数据包含一个高分辨率的DEM和一个低分辨率的DEM，其中低分辨率DEM是高分辨率DEM降采样的模拟DEM。第1步，分别从高分辨率和低分辨率DEM中获取坡度图；第2步，将高分辨率DEM提取的坡度图降采样到与低分辨率坡度图相同的分辨率；第3步，计算低分辨率坡度的拉普拉斯滤波图；最后，使用70%比例的数据进行回归，30%比例的数据进行检查。拟合结果见表1。

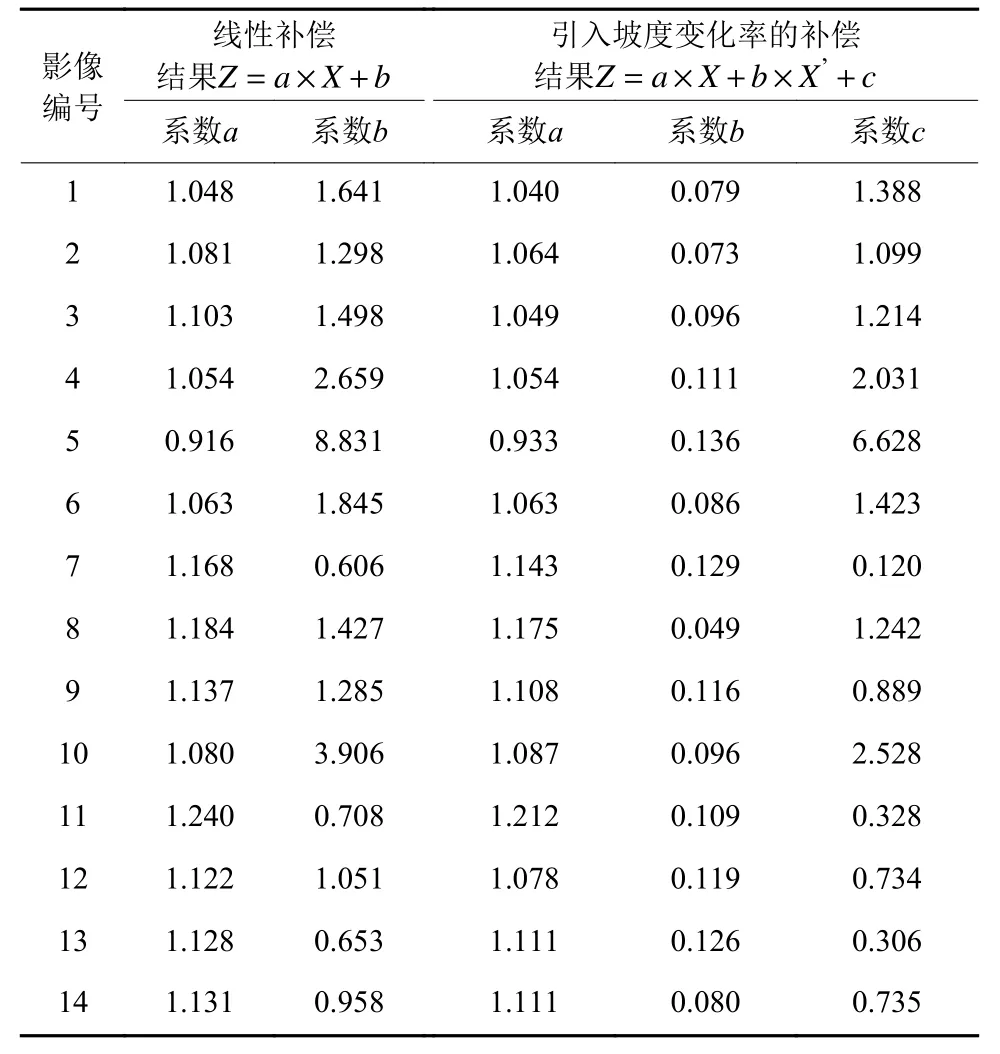
表1 月球数据拟合结果Table 1 Fitting results of lunar data

同理，对6个火星区域的坡度进行参数拟合，拟合结果见表2。

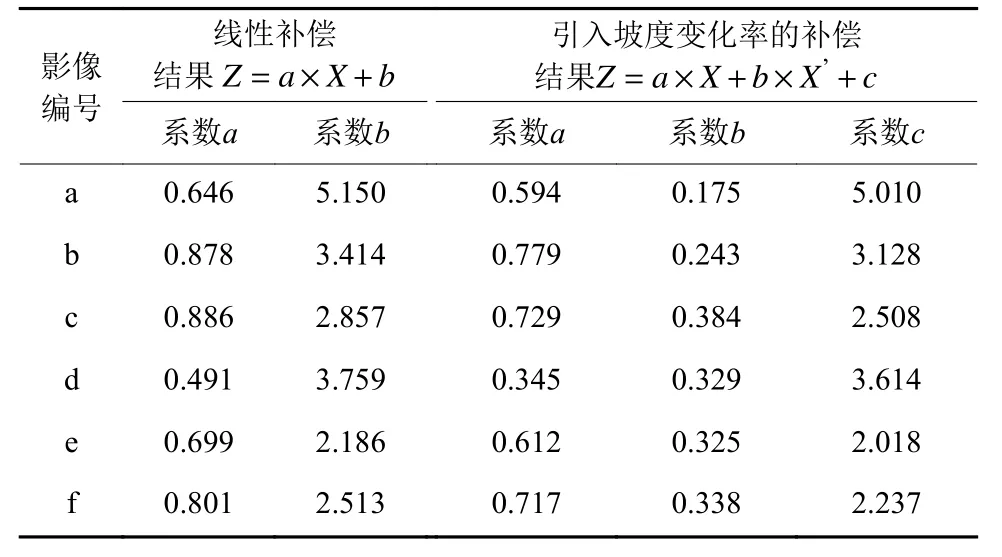
表2 火星数据拟合结果Table 2 Fitting results of Martian data

本文使用平均绝对误差（Mean Absolute Error,MAE）和均方根误差（Root Mean Square Error,RMSE）作为评价指标。MAE（表示为EMAE)和RMSE（表示为ERMSE）的计算方法如下

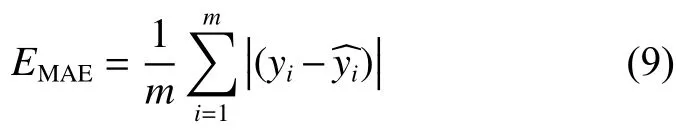
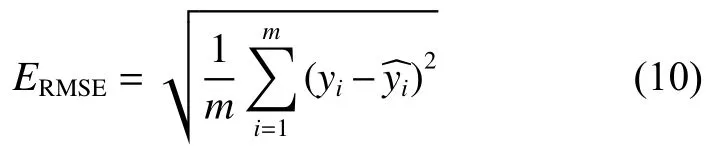
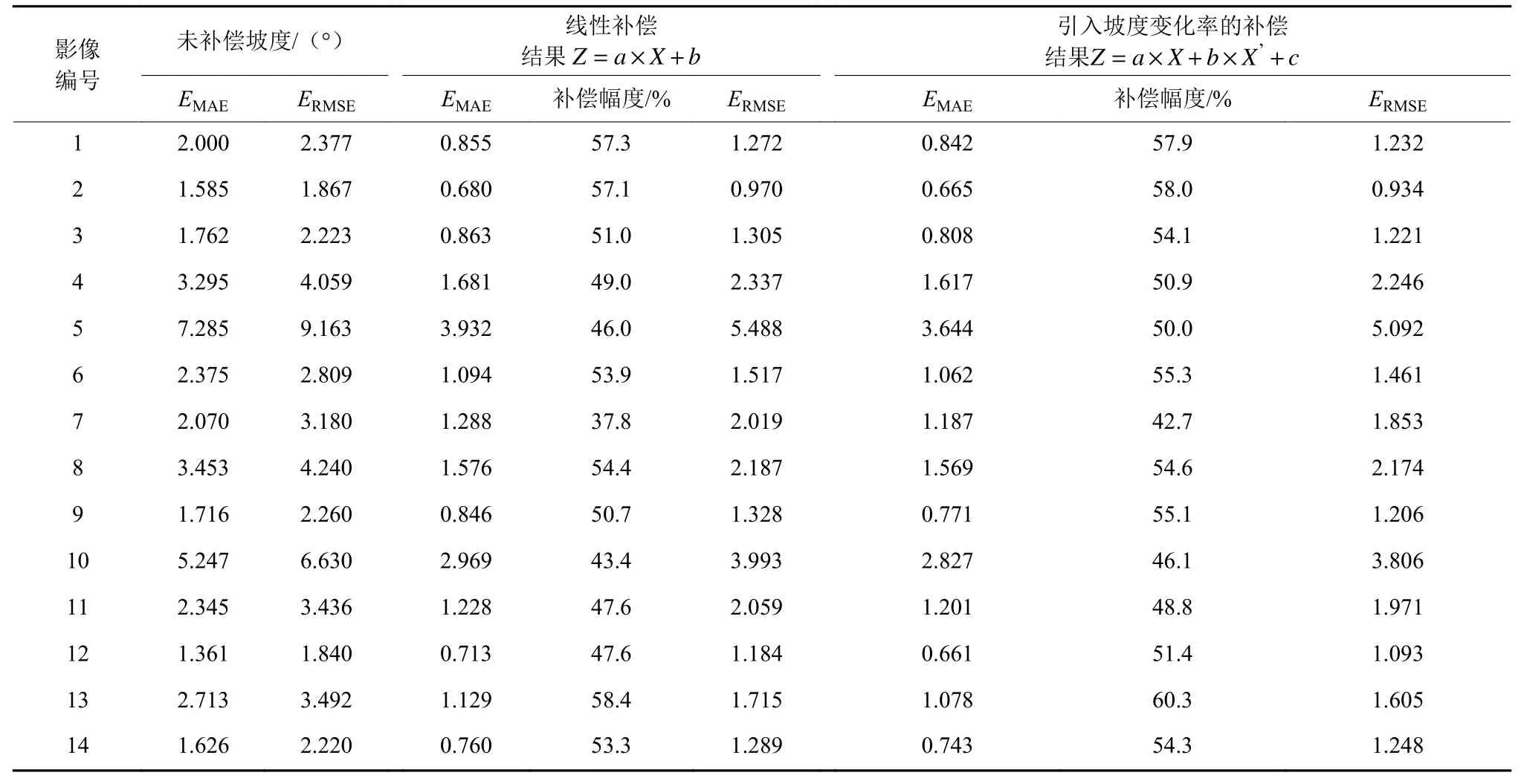
表3 月球补偿实验精度评价Table 3 Evaluation of lunar data experiments

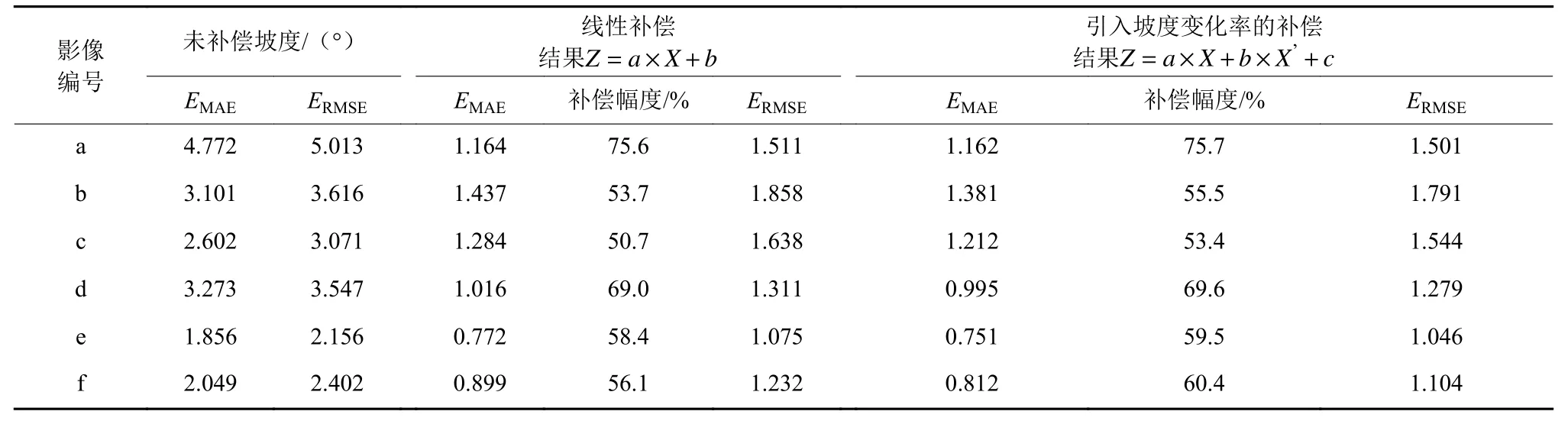
表4 火星实验精度评价Table 4 Evaluation of Martian data experiments

3 应用研究

3.1 月球多地形整体补偿模型及分级补偿模型

上文图4所示的这14幅数据覆盖了不同的地形特征，可以作为月球多种典型地形坡度的代表数据。从这14个区域内获得有效数据共45 578 385组，随机选取有效数据的70%作为模型训练数据，30%作为测试数据，采用引入坡度变化率的坡度补偿方法，拟合得到月球多地形整体坡度补偿模型。该补偿模型设定高分尺度为5 m，低分尺度为20 m。表达式见式（11），评价结果如表5所示。

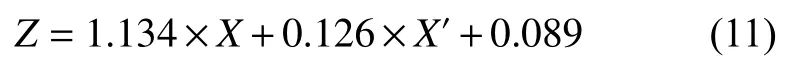
表5 月球多地形整体补偿模型精度评价Table 5 Evaluation of compensation model for global moon

将全月坡度分为0°～3°，3°～6°，6°～9°，9°～12°，12°～15°，15°～20°，20°～30°，30°以上，共8级。确定分级标准后，将月球上的低分尺度坡度数据逐一划入对应的分级范围内，同样，在各个分级内，随机抽取70%的数据用于模型拟合，其余30%的数据用于模型检验。对每个坡度范围内的数据分别利用引入坡度变化率的补偿方式进行模型拟合，即可得到每个坡度范围内的模型。理论上应相对于整体数据所得到的模型更适用于对应坡度范围的补偿工作,因此可在整体补偿模型表现不佳的坡度范围内，使用对应的分级补偿模型进行补偿。模型拟合及模型检验结果如表6所示，结果表明：大部分分级范围内，整体模型与分级模型的效果接近，可根据实际情况选择二者之一，但在坡度大于20°时，整体补偿模型效果较差，此时可辅以分级模型以得到更优的补偿结果。

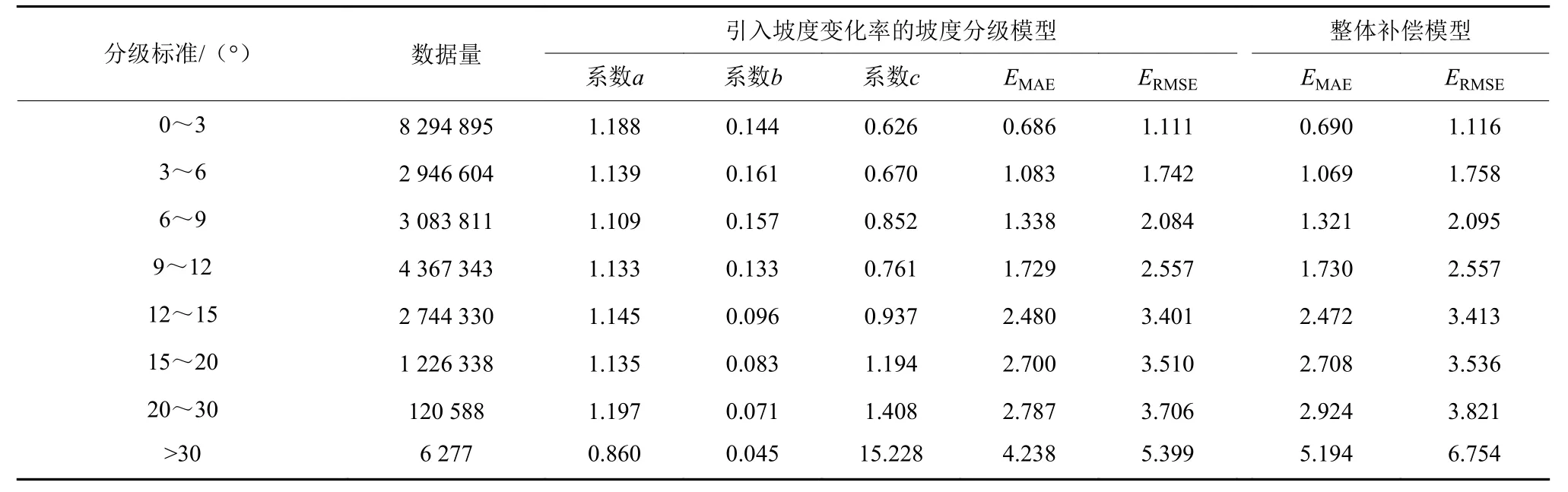
表6 分级坡度拟合和检验结果Table 6 Fitting and validating results of graded lunar slopes

3.2 “天问一号”着陆区坡度分析

中国发射的“天问一号”火星探测器于2021年5月15日成功着陆于火星的乌托邦平原，着陆器携带的“祝融号”火星车已在火星表面开展巡视探测任务。乌托邦平原地表相对平坦，撞击坑和石块等分布较少，据推断，该地区近地表含有大量水冰，对该地区的研究，对于了解水在火星演化中的作用甚至是潜在宜居性具有重要的意义[21]。着陆区的坡度对火星车的行动能力具有重要影响，研究人员使用MOLA DEM提取坡度数据发现，坡度大的区域多位于撞击坑的边缘和高原与平原的交界处，而乌托邦平原内部则坡度较小[22]。大尺度坡度分析可服务于着陆区地质概况研究，然而火星车行进可达性分析则需要更加精细的坡度。

在着陆点附近并没有大范围的高分辨率HiRISE DEM，选取覆盖“天问一号”着陆点50 km×50 km范围的200 m分辨率的HRSC-MOLA融合DEM，基于该数据，提取得到200 m分辨率的坡度图，将区域内仅有的两幅小范围HiRISE DEM数据制作生成坡度图，作为参照值进行补偿精度的评价，上述实验数据的覆盖范围如图7所示，图中大范围数据为HRSC-MOLA融合DEM，黄色框和绿色框中的小范围数据为HiRISE DEM，红色五角星为“祝融号”火星车着陆点。

图7 实验数据范围Fig.7 Experimental data coverage

采用该区域内的两幅HiRISE DEM及其降采样的DEM作为拟合数据，同2.2节的步骤，拟合生成的适用于该区域的200 m分辨率的坡度补偿模型为式（12）

采用该式对50 km×50 km范围的HRSC-MOLA坡度进行补偿，以HiRISE数据作为标准值，对补偿结果进行评价，评价结果见表7。补偿前后的坡度图如图8所示，两幅HiRISE DEM覆盖区域的数据对比如图9所示。由图8及图9可见，通过补偿，坡度得到了整体放大，提升了地形模型的细节丰富度。

表7 补偿前后对比分析Table 7 Comparison analysis before and after compensation

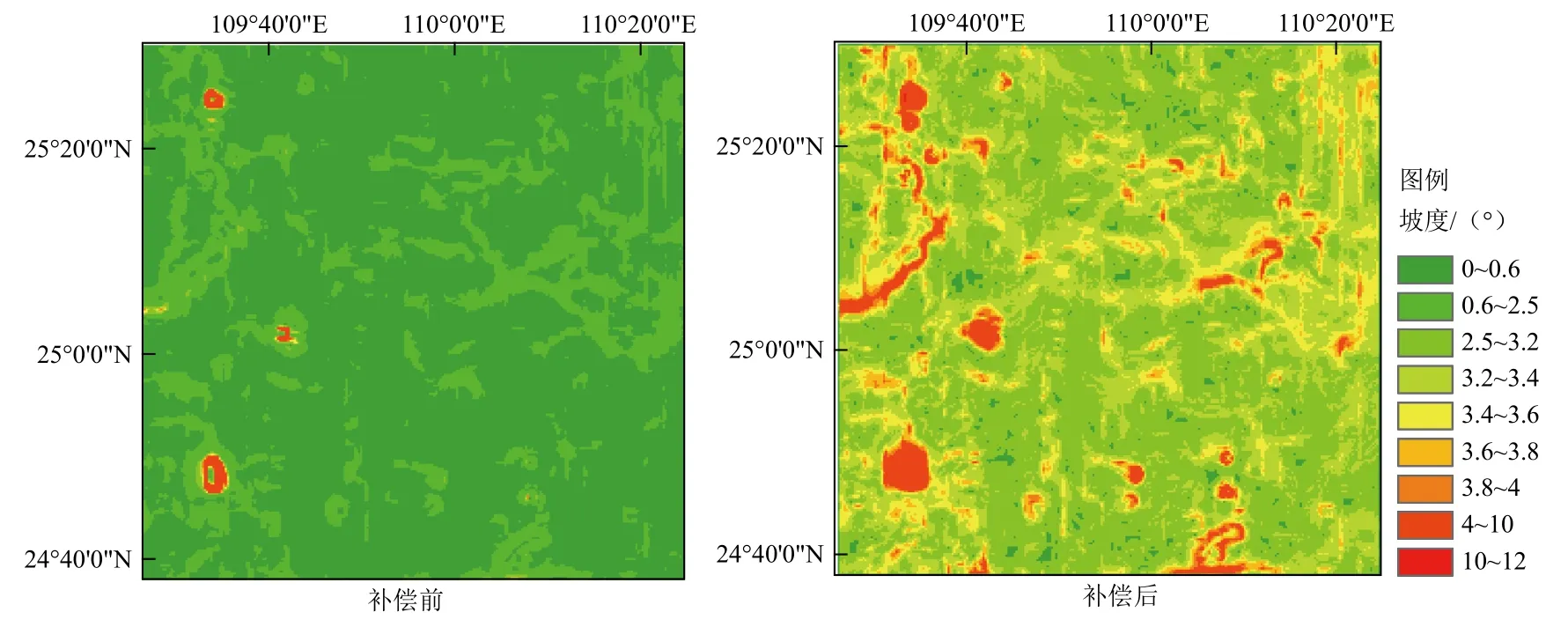
图8 HRSC-MOLA补偿前后坡度对比Fig.8 Slope map before and after compensation

图9 HiRISE坡度以及HRSC-MOLA坡度补偿前后对比Fig.9 HiRISE slope and HRSC-MOLA slope before and after compensation

4 结 论

提出了一种改进的低分辨率坡度补偿方法，在传统的一元线性补偿方法基础上，考虑到坡度变化率的影响，使用拉普拉斯算子提取低分坡度变化率信息，并将其作为自变量之一，嵌入至补偿模型中。主要得到了以下结论。

1）以覆盖全月多种地形的14个区域以及“天问一号”着陆区乌托邦平原的6个火星区域作为实验区，利用从高分辨率的LROC NAC DEM和HiRISE DEM提取出的坡度作为参考值，逐区域利用引入坡度变化率的补偿模型与已有的一元线性模型对从降采样的LROC NAC DEM和HiRISE DEM提取出的坡度进行补偿。结果表明：不论何种地形特征，不论月球场景还是火星场景，利用引入坡度变化率的补偿方法所得到的精度均优于传统的线性补偿方法。本文方法也可用于其它类型地表的坡度补偿，由于数据限制，本方法只在月球和火星场景下进行了验证。

2）利用本文的补偿模型，提出了适用于月球多种地形的低分辨率坡度补偿方法，并给出20 m分辨率DEM对应的坡度补偿到5 m量级对应坡度的整体补偿模型参数。结果表明：应用整体补偿模型至分级的坡度补偿时，在低坡度区域，整体补偿模型与分级模型效果接近，而在高坡度区域，整体补偿模型表现相对较差，此时可辅以分级模型作为整体模型的补充。

3）对覆盖“祝融号”火星车着陆点50 km×50 km的HRSC-MOLA低分辨率坡度进行补偿，与该范围内的一幅1 m分辨率的HiRISE坡度进行比较，补偿比例达到80%以上，补偿后的MAE和RMSE均小于1°，与补偿前相比，地形细节丰富度有一定程度的增加，再次证明了该方法的有效性。