基于河流与含水层相互作用的河流污染物运移模型研究
2022-06-30曹红胜张琳
曹红胜 张琳
(1. 滨州市政务服务中心,山东滨州 256600;2. 滨州市引黄灌溉服务中心,山东滨州 256600)
1 引言
随着我国城镇化的不断推进,居住在城市周边地区的人口数量越来越多[1-2],如何有效保护水资源以及避免河流污染损害人类和生态健康成为一大挑战[3-5]。目前,固体废物和水污染是城市河流的主要污染源,并且人口的快速增长与基础设施建设之间的不平衡,也使得河流中存在大量的病原体和有机物质。此外,大量文献研究表明[6-8],尽管城市地区的地表不易透水,但污染物仍会渗入地下污染地下水源,再加上过度抽水,各含水层间的相互作用增强,加剧了污染物在地下水系统不同层间的传播和运移,使问题进一步恶化[9]。这种变化会影响河流的水利状况,反过来也会加剧水质污染问题,因此,需要针对河流含水层系统的管理采取更加综合有效的措施。
确定产生河流和含水层系统流动与运移动态的环境,对解决河流污染问题至关重要。然而,目前人们对此过程了解甚少,而且缺乏适当的模型来模拟河流与含水层间的相互作用,无法获得污染物的运移情况。因此,本文提出了一种基于河流与地下水空间耦合分布的河流走廊污染物运移模型,该模型克服了现有单一系统建模方法和集水区尺度水文模型的局限性,真实模拟了河流走廊中河流和含水层之间的相互作用及污染路径,有利于调查现有污染的影响,为提出相应的管理策略提供依据。
2 模型的建立
2.1 典型模型分析
河流和地下水交换流量与质量的速率是随空间和时间变化的,取决于界面处的水力和水质特征。由于流量和质量的交换速率是动态的,因此会出现非线性交换模式。
为了描述该现象,需要建立耦合地表水(SW)和地下水(GW)成分的水文模型。已有的模型包括MODHMS,InHM,HydroGenoSphere,MIKE-SHE,tRIBS。但是,上述模型的比例尺虽然可以通过假设来简化陆上水流路径,但对于河段和走廊比例尺研究而言,此类简化仍然是不合适的,尤其是不适合模拟洪水和湍流等现象以及相关的输运过程,因为它们需要更详细的信息。
随着计算机的进步,耦合地表非稳定水动力和地下水流动解算器的模型逐渐成熟,包括SWIFT2D-SEWAT,MODFLOW LGR VSF newCFL,MODFLOW-OWHM 和2dMb MODFLOW。
但是,二维地表水流模型和三维地下水流模型的完全耦合仍处于起步阶段,均没有考虑洪水和湿地研究的移动边界问题,仍未在输运和水质耦合方面取得进展。
目前有多种典型的地表水和地下水模型,通常只适用于模拟河流或含水层的动态情况。但是,由于以下原因,它们不适用于涉及瞬态条件、不规则形状河床的复杂情况下的河流含水层流量和质量估算:
(1)大多数是为解决典型河流或含水层问题而开发的单一系统模型。虽然针对影响系统的过程进行了相应的建模,与其他非建模系统相互作用产生的过程仍需要一组边界条件,但是边界条件的定义在多数情况下被简化并且不符合实际情况。
(2)河道和漫滩中河流与含水层的相互作用是一个复杂的动态过程。相互作用的方向取决于地下水位和河流水位的相对位置。但是,河流与含水层之间的流量和质量交换通常被忽略或简化为均匀或线性变化的预定义速率,这与实际情况是不符的。
(3)可能发生界面通量方向的反转,从而导致每个系统交替充当源或汇。因此,河流-含水层界面的物质交换的模拟,受不断变化的压力梯度和作为源头的整个系统的浓度分布的影响,需要并行求解河流与地下水流动和输运方程,同时根据相互作用的变化不断更新地表水和地下水系统状态。对于外部耦合河流和地下水模型,一般无法计算由河流-含水层相互依存的动力学引起的流量振荡。
2.2 新模型构建
2.2.1 模型架构
本文所建立的模型主要将两种运移模型(QeS2用于地表水[10],MT3DMS 用 于 地 下 水[11])明 确 地耦合到一个整合的河流-含水层流动模型(2dMb+MODFLOW)中。该模型不仅规定了流动和运移方程的联立解,还计算了水和示踪剂在河流与地下水系统连续体中的交换通量[12-15]。模型架构及模拟过程的简化表示如图1 所示。
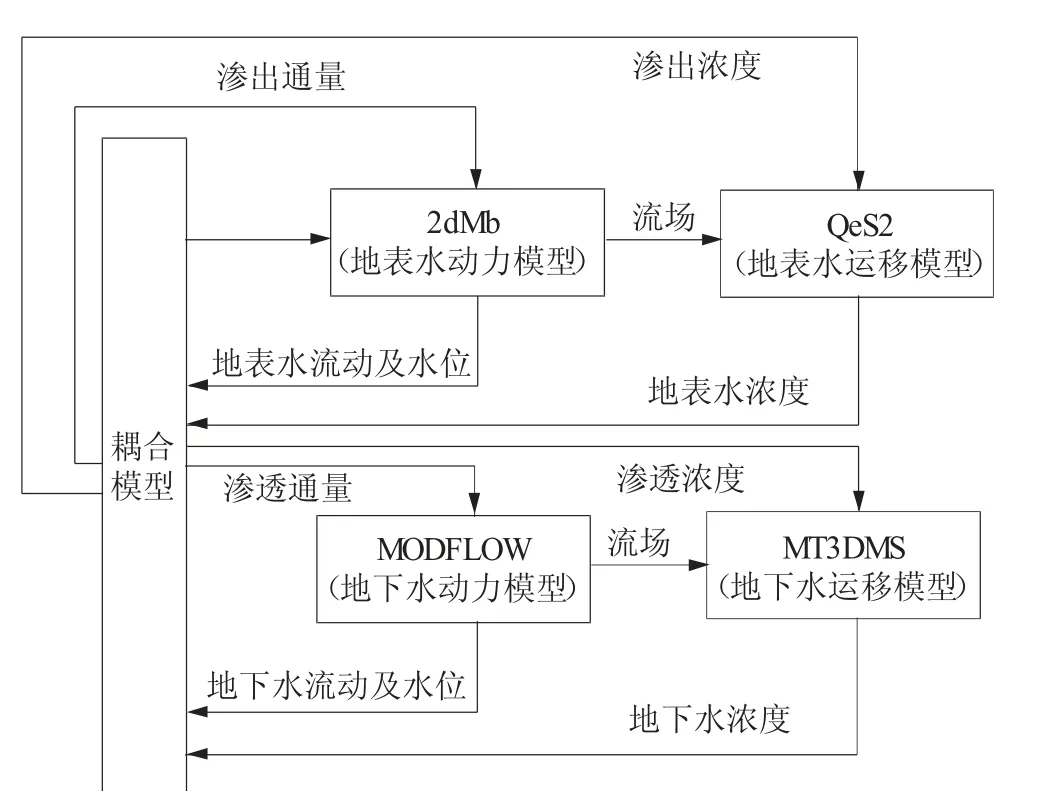
图1 模型架构及模拟过程的简化
地表水动力与运移模型部分分别为2dMb 和QeS2 模型的修改版本,主要用于求解二维欧氏空间中的二维深度平均浅水和运移偏微分方程。由于地形的离散化用来获取河流走廊区域的地表流和运移动态,因此无需指定河流的位置。2 个地下水模型部分分别为MODFLOW 和MT3DMS 的修改版本,主要用于求解二维/三维地下水流动和运移偏微分方程。每个流动模型组件中所使用的时间步长需要独立计算,并且在整个模拟过程中要不断更新,以符合Courant(CFL)条件。一般来说,河流模型的时间步长通常为秒或1/10 秒,具体取决于网格分辨率和流量条件。而地下水模型所需的时间步长通常为小时或天,比河流模型所需的时间步长高出104倍。
2.2.2 污染负荷方案
河流的污染源类型主要分为点式和分布式两种[16]。其中,第一种类型主要包括模拟溢出型负荷的瞬时点源和模拟出口型负荷的连续点源。后者主要包含线性斜率算法方案,因为它可以通过逐次线性逼近而适用于几乎任何负荷模式[17]。瞬时点源和连续点源分别由以下方程式描述:
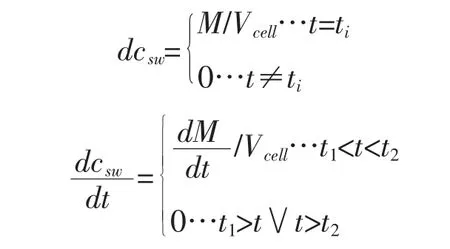

式中,Km为负荷率,%,主要取决于移动河床特征或自由水面面积。
2.2.3 模型设置与参数化
用于测试(瞬态)传输部分的解析解需要稳态和均匀的流场以及给定的色散系数,然而,SW 和GW流量部分产生此类条件的边界条件与参数的定义并不直接,需要进一步考虑。在GW 流量分量的情况下,纵向压力梯度和水力传导率被定义为产生0.33 m/s的渗流速度,该速度使用达西定律估算,并可直接用于解析解。将横向压力梯度和电导率分别设置为0和Kx×10-5,以使流场为单向且沿纵向方向。在基于电导的模型部分中,参数kc/b(电导层厚度上的电导)值范围在1~0.001 m/d 之间,在本模型中,使用的值为0.043 2 m/d。为了确保受地表水体渗透影响的含水层中流场的准确估计,地下水网格单元分辨率不应超过特征长度,因此,其值设置为10 m。
初始和边界条件以及所用污染源的特征见表1。为了便于验证模型,定义了2 种不同的场景“S1”和“S2”,分别测试SW 和GW 污染物传输部分以及SW-GW 相互作用模型部分。场景“S1”包括2 个连续的污染负荷点,1 个位于河流中,另1 个位于地下水中,分别测试SW 和GW 运输模型部分的性能。场景“S2”旨在测试SW-GW 交互模型,仅使用边界和初始条件进行强制。
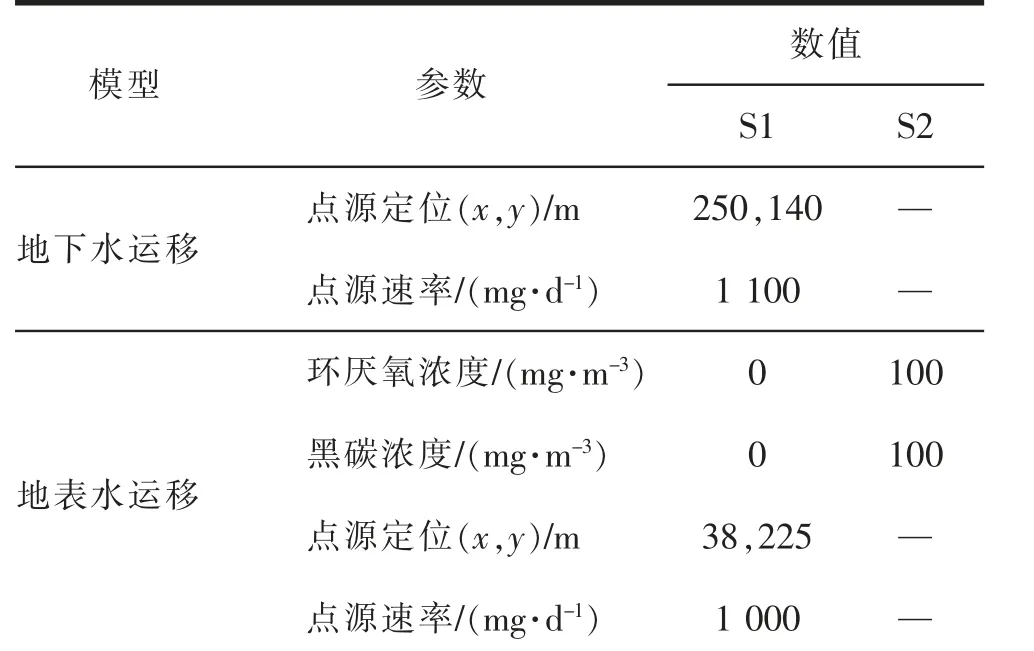
表1 初始和边界条件以及所用污染源的特征
3 结果与分析
用于测试传输组件的分析解决方案要求在整个区域内具有稳态和均匀流动条件。为了确保基准问题满足上述条件,首先测试模型是否能够再现所需的流场。
3.1 地下水运移
通过模拟结果可知,形成了均匀、稳定和单向的压力梯度,并如前面所设计的一样形成了0.33 m/s的稳定渗流速度。将GW 传输部分的数值结果与2个不同时刻的相应解析解进行对比,结果表明,模型结果与解析解非常吻合,其中具有微小的差异,主要是由数值色散引起的,误差在可接受的范围之内。
3.2 地表水运移
基于分布场景“S1”中达到稳态流动条件后的水位、速度、剪切速度、湍流黏度和扩散率分布结果,稳态条件非常接近,只有微小的偏差。由于区域大小有限及摩擦,河岸附近的速度较小。此外,由于北部和南部边界条件的影响,导致了涡流扩散率和涡流黏度在这些区域分布也不均匀。但是,基准问题的范围涵盖了较广泛的区域,该区域不受非均匀行为的影响,可根据分析解决方案对SW 传输组件的性能进行测试。所选区域的稳态证据中,所有与流量相关的变量在该区域中都是恒定的,并用阴影交叉线突出显示。只有涡流扩散率沿流动方向略有变化,但与平均值的解析解中使用的值相对应。将数值解与解析解进行比较,结果表明,数值模型很好地捕捉了解析解在空间和时间上预测的总体浓度分布。微小差异是由SW 流分量模拟的驱动流变量的可变性以及数值解中遇到河岸的羽流引起的,其影响随着时间的推移变得更加明显。与地下水模型部分的误差类似,可比区域的绝对误差小于1%。
3.3 河流-地下水相互作用:流动和运输
基于电导率模型中的输运分量没有解析解,因此,当外部耦合时,采用耦合模型得到的场景“S2”的结果与MODFLOW 和MT3DMS 独立版本预测的结果进行比较。由结果可知,2 种模型方法模拟的渗透通量相似,表明所建立的新型模型准确性较高,在边界附近的预测不匹配主要是由于表面流和运移模型中边界条件的影响。
4 结论
(1)基于河流与地下水空间耦合分布的河流走廊污染物运移特征,本文建立了相应的数学模型,将目前已有的多个独立模型完全耦合到河流的运移过程中。建立该模型是为了解决现有单一系统建模方法和现有尺度水文模型的局限性,提供一种分析复杂现象的方法。
(2)模拟结果表明,与现有单一系统模型结果相比,新型河流污染物运移模型能够更准确地模拟相连河流含水层系统中的污染路径,并且在当前城市高速发展的背景下,有利于调查现有污染的影响,并为提出相应的管理策略提供依据。
(3)虽然该模型仍存在一些局限性,但对城市河流污染的预防和恢复有着重要的指导意义,可在进一步了解水文系统之间的复杂相互作用及发生在河流含水层界面上的水力和生物化学过程基础上,不断更新及优化该模型。
