密集线性台阵地震背景噪声速度成像及其在湖南沃溪金钨锑矿勘探中的应用

王 悦，刘江山，沈长明，邓 宝，苏文君柳，陈棋福，李俊伦*

1.中国科学技术大学 地球和空间科学学院，合肥 230026；

2.湖南省有色地质勘查研究院, 长沙 410015；

3.中国科学院 地质与地球物理研究所，中国科学院 地球与行星物理重点实验室，北京 100029

1 引言

地震学是人类认知地球内部结构的一种不可或缺的研究手段。大尺度的研究区域主要依赖于天然地震的观测数据，而小尺度局部区域的研究一般依赖于勘探手段。近年来，面波勘探技术发展迅速，有关瑞利波的研究大量问世。瑞利面波勘探作为一种新型浅层地震勘探手段，对浅地表结构具有高分辨能力，目前已经广泛应用于油气开采、城市地下空间勘察、无损检测等方面（宓彬彬，2018）。如何从原始地震记录中准确提取频散曲线，并利用频散曲线反演地下结构是面波勘探技术的关键。

多道面波分析方法（MASW）（Park et al., 1999）是近二三十年来最流行的面波分析方法。常用的面波分析方法有F-K法（Capon，2005）、τ-p变换法（Mcmechan and Yedlin, 1981）、相 移 法（Park et al.,1998）、拉东变换法（Luo et al., 2009）等。F-K变换法具有方法简单的特点，将二维时域信号进行傅里叶变换，转换为F-K域上的信号。但F-K变换法要求空间和时间域采样间隔相等，如果波形记录中存在坏道，会对结果产生较大影响(卢建旗，2013)。τ-p变换法和拉东变换法均将数据进行倾斜叠加, 对高阶信号分辨率较好, 但基阶频散曲线在低频段成像效果较差（邵广周和李庆春，2010）。相移法先对时间域信号进行傅里叶变换之后对幅值进行归一化处理，在空间域进行积分, 通过在不同频率下的速度扫描来提取频散曲线, 更适用于提取基阶频散曲线（邵广周和李庆春，2010）。对F-K法、τ-p变换方法和相移法进行对比发现，相移法在计算效率、抗噪性和灵活性等方面都优于其他两种方法（Dal Moro et al., 2003）。

背景噪声技术近年来广泛应用于研究近地表三维速度结构。其基本思想是通过计算台站对之间的噪声互相关函数来近似得到台站对间的经验格林函数。通常，高频面波对浅层结构比较敏感，低频面波对深部结构比较敏感（Li et al., 2016）。早期的背景噪声成像研究主要利用长周期的面波频散反演地壳和上地幔结构（Yao et al., 2006, 2008; Lin et al.,2007）。近年来，背景噪声互相关方法在提取高频面波信号反演浅层速度结构方向取得了显著进展（Lin et al., 2013; Fang et al., 2015; Du et al., 2020）。

基于背景噪声技术和相移法的特点，我们提出了一种新的方法——拓距相移法，提高传统相移法对低频信号的提取能力。拓距相移法分为阵内相移和阵外相移两部分，利用阵内相移对小孔径范围的中高频信号进行提取，用阵外相移对大孔径范围的中低频信号进行提取，然后将两部分频散曲线整合得到一条宽频带频散曲线。本着发展新的有效物探手段进行深部找矿的根本目的，同时为了检验拓距相移法的有效性，我们在湖南沃溪布设了多条被动源密集测线，在2019年9月到2019年10月进行了为期一个月的连续数据采集，提取频散曲线后反演得到地下横波速度结构。成像结果与已知断层、岩性分界面、矿脉等有着较好的对应关系。本文将从方法介绍、矿区地质概况、互相关计算、频散提取、速度结构反演、地质解释与分析等方面进行阐述。湖南沃溪矿区成像案例证实了拓距相移法可以有效拓宽频带宽度，对于近地表地下资源勘探有着重要意义。

2 方法原理

2.1 相移法

传统相移法主要原理（Park et al., 1998）假设位于 x 处的地震仪在 t 时刻接收到的地震记录为u(x,t)，通过时间域傅里叶变换得到其频谱

其中，A(x,)ω是振幅谱，包含了衰减和几何扩散等特性，P(x,ω)=e−iψx是其相位谱（为地下真实的相速度），包含了全部频散信息。我们可以对频谱进行归一化以消除振幅谱的影响，

对=(x,)ω在空间域做积分得：

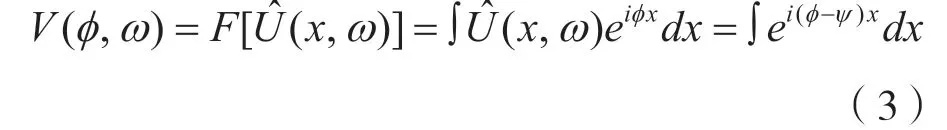
为了提高传统相移法频散成像的效果，本文将互相关函数与传统相移法结合，在相移法基础上，利用所有道的相位差信息。同时，为便于实际数据处理，我们将式（3）积分形式离散化，对于N道数据，得到

当cT=cR时，频散能量达到最大值。同样，可以进行速度扫描，来获得频散能量图。

实际情况中，由于噪声源分布、仪器响应和地表起伏等因素的干扰，我们采集到的信号中存在不相干的随机噪声干扰，仅用一对台站计算得到的频散能量稳定性差。在实际应用中，为了提高稳定性及施工效率，我们将一条长测线划分为许多次级台阵，在次级台阵内部计算台站对的频散能量，并进行叠加平均，得到较稳定的频散能量图。

2.2 拓距相移法

传统相移法对于高频信号的提取较为有效，但处理低频信号时易受到线阵孔径的影响，为了提高对中低频信号的提取效果，我们在传统相移法的基础上提出了拓距相移法。

拓距相移法由阵内相移和阵外相移两部分组成。图1是一条密集测线台阵的拓距相移法示意图，以某一台站为中心划分一个次级台阵，分别利用阵内相移和阵外相移各提取一条频散曲线。阵内相移易于提取高频信号，而阵外相移易于提取中低频信号。将分别提取的中低频频散和高频频散整合成一条完整的频散曲线，再对频散曲线反演得到速度结构。

图1 拓距相移法示意图Fig.1 Sketch showing the extended range phase shift method

2.2.1 阵内相移

由于阵内相移处理过程中不涉及次级线阵外部台站，阵内台站的拓距相移法类似于传统相移法。在处理过程中，我们分别以一条密集测线上的每个台站为中心，以一定半径划分次级线阵，获得许多次级线阵。对每个次级线阵中的台站对之间计算互相关函数，通过相移法获得这一次级线阵的频散能量图。通过不断移动中心台站的位置，我们就可以获取全部台站下方的频散信息。

2.2.2 阵外相移

阵外相移利用的地震数据既包含次级线阵内部，也包含次级线阵外部。在处理过程中，我们以

2.2.1 中同样的方式获得许多次级线阵。对于一个次级线阵，将阵外的每一个台站视为虚拟源。对于同一个虚拟源，将阵内的所有台站视为接收器，计算该源和全部接收器的频散能量。

假设研究第 n 个台站下方结构，我们将其作为中心台站，划分次级线阵时两侧各包含m个台站，线阵内部包含 2m+1 个台站。对线阵外的第 k 个源，计算该源和次级线阵内全部台站的频散能量 V ：

将传播路径分为阵内、阵外两部分

公共的阵外路径部分可提前到求和符号外部

当cT=cR时，频散能量达到最大值。我们对每个虚拟源都进行同样的运算，得到多个频散能量图。虽然不同源到同一次级线阵的路径各不相同，但对中低频频段的信号而言，波长较长，衰减较慢，不易散射，我们可以认为信号在次级线阵的外部区域传播路径基本一致，此时仍然是次级线阵内部区域对频散能量起主导作用。因此，我们可以对这些不同虚拟源得到的频散能量取绝对值以消除阵外公共路径影响后进行叠加平均，获得的频散能量图作为线阵中心台站的阵外频散能量。

对于衰减快，易散射的高频信号，本身受地表起伏影响更大，远台间距的互相关函数信噪比较低，且其在阵外区域的传播路径更加复杂，叠加过程不能保证有效提升频散能量质量。因此，阵外相移对中低频信号的频散提取更加有效。

2.3 反演方法

我们通过阻尼最小二乘法，将利用拓距相移法提取出的宽频带频散曲线反演得到地下横波速度结构剖面。反演的最小化目标函数为

其中d为观测数据，即相速度频散曲线，m为横波速度模型，G为敏感度矩阵，L为模型的有限差分近似算子，α为阻尼系数。频散曲线的正演计算利用CPS软件包（Herrmann，2013），通过经验关系式（Brocher, 2005）由横波速度得到纵波速度、密度，从而正演得到瑞利面波相速度。通过迭代进行求解，已有的单点反演方法根据如下方程计算速度模型更新：

式（9）中δd为观测值与现有模型理论值的偏差，G为当前模型下的敏感度矩阵，Lv为垂直方向有限差分近似下的拉普拉斯算子，λv为垂直方向的阻尼因子，δm为进行一次迭代的模型速度修正量。式（9）括号中第一项用于反演速度结构，第二项用于约束模型垂向变化，在此基础上，我们加入横向约束来约束模型水平变化，以提高反演过程鲁棒性，有

Lh为水平方向有限差分近似下的拉普拉斯算子，λh为水平方向的阻尼因子。计算得到模型更新量后进行迭代，有

mk为第k次迭代后的速度模型，δmk为第k+1次迭代的修正量，mk+1为第k+1次迭代修正后的速度模型。通过反演获得横波速度模型的更新量，然后对新的速度模型进行正演获得相速度的敏感核矩阵，之后对相速度进行更新，不断迭代更新模型，直至反演收敛。

3 台阵布设与数据采集

湖南省是我国黄金生产大省之一，开采黄金历史悠久，最早可追溯至春秋战国时期。由于长期的开采，矿产资源逐渐短缺，地表浅部大部分矿产已被发现，预测和找矿难度不断增加。此外，矿区大多地处山区，地质环境问题复杂，地质灾害频发。如何高效地勘察地质结构，提升工作效率，是当今地质矿产行业的重要目标。

3.1 地质背景

勘探资料证实，湖南省内黄金矿区主要分布于雪峰山金、锑、钨的成矿带上。其中，湘西沅陵县境内的沃溪金矿位于雪峰弧形构造隆起带中段，是江南古陆金矿成矿带上一个金、锑、钨共生的大型矿产，具有重要的勘探价值（匡文龙等，2004）。对于矿区地层和构造的进一步认识，有助于速度结构反演以及地质解释工作。

3.1.1 矿区地层

湖南沃溪矿区出露地层主要为冷家溪群、板溪群、白垩系。根据沈长明等（2017）①沈长明，刘江山.2017.湖南省有色（贵）金属矿山深边部找矿综合物探方法有效性研究报告[R].湖南省有色地质勘查研究院.、匡文龙等（2004）给出的沃溪金矿地质特征，研究区域的地层从老至新分别为：

（1）冷家溪群（Pt2lj）：为灰绿色绢云板岩，局部夹浅变质石英岩、砂岩及少许凝灰质砂岩，与上覆板溪群不整合接触。

（2）板溪群（Pt3bn）：是矿区内分布最广的地层，自下而上分为：马底驿组（Pt3bnm）和五强溪组（Pt3bnw）。

马底驿组（Pt3bnm）又可分为上下两段

(a)马底驿组下段（Pt3bnm1）：为灰绿色变质砂岩，呈带状分布，厚度在100 m左右。

(b)马底驿组上段（Pt3bnm2）：为紫红色、灰紫色条带状板岩、砂质板岩、含钙板岩，其中含钙红色绢云母板岩、砂质板岩是金锑钨矿的主要赋矿岩性。底部夹灰绿色板岩、砂质板岩及中细粒砂岩，中、上部有钙质条带及钙质结核。该地层为区内出露的最主要地层，广泛分布于沃溪大断层下盘、矿区中部，与白垩系、震旦系地层呈断层接触。

五强溪组（Pt3bnw）：为青灰、灰绿色中厚层变质纹带状石英砂岩，夹砂质板岩、板岩，呈东西向分布。五强溪组和马底驿组, 两者之间呈断层接触。

（3）上白垩统（K2）：为巨厚层状红色、棕红色砂砾岩，不整合覆盖于板溪群地层上。

3.1.2 矿区构造

矿区西南部为仙鹅抱蛋穹隆状复背斜，东南部为拖毛岭复背斜，中部为沃溪—唐浒坪反“S”型构造（汪劲草等，2000）。矿区主要为近东西向的构造。区域性的沃溪大断层（F1）横贯矿区，呈近东西向，倾向北，倾角约30°，长达20 km（李键炎，1989）。断面常呈舒缓波状，破裂带宽为20~130 m，构造岩主要由碎裂板岩、角砾岩、碎粒岩、糜棱岩和断层泥组成（黄瑞华等，1998）。

图2 沃溪地区地质构造简图Fig.2 Regional geological map of the Woxi W-Sb-Au deposit

其次，矿区内有多条较大的层间断裂，走向长650~5300 m，与沃溪断层（F1）呈“入”字形相交，沿走向呈舒缓波状，断层面上有断层泥，厚度为1~20 cm。层间断裂的规模和形态控制着蚀变带及其中矿体的形态和规模，在层间断裂倾角变陡处，层间脉矿化减弱，矿脉变薄；反之矿化则增强，矿体变厚（匡文龙等，2004）。

矿体主要产出形态是层脉。层脉沿层间断裂充填，产状与岩层基本一致。层间脉的构造特征反映了变质热液成矿的特征（陈吉华，2018）。

3.2 密集台阵的布设

沃溪金矿划分为五个矿段，分别为红岩溪、鱼儿山、粟家溪、十六棚公、上沃溪（沈长明等。2017）。本次研究区域沃溪金矿的粟家溪矿段，处于鱼儿山和十六公棚两个矿化富集中心的过渡部位，地势南高北低，海拔在150~700 m之间。

基于密集台阵的背景噪声成像方法具有绿色环保、分辨率高等优点。为了研究该区域的地质构造，我们选择线性密集台阵，跨区域性断层F1和F2布设8条密集测线进行二维剖面采集。图3展示了研究区域的台站分布和地形特征，沃溪大断层F1呈近东西向，唐浒坪断层走向近北东向。8条测线平行分布，方位角为160°，长度均为10 km。此次数据处理选取了其中的3条测线，其中，160测线台间距为 200 m，360测线台间距为400 m，505测线基本台间距为250 m，中段4 km重点研究区域加密至100 m。

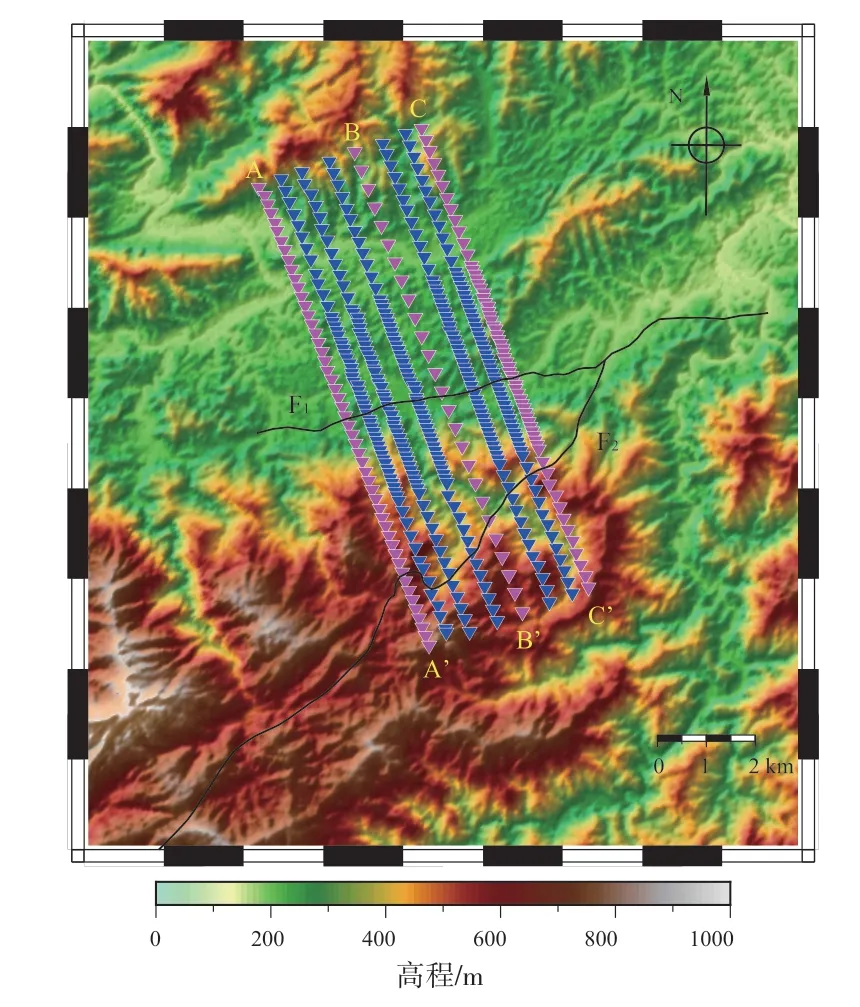
图3 8条密集测线的台站分布Fig.3 The distribution of stations of the 8 dense arrays

3.3 数据采集

笔者采用467台主频为5 Hz的SmartSolo节点式短周期地震仪，在2019年9月到2019年10月进行了为期一个月的连续数据采集。相较于宽频带地震仪，短周期地震仪具有体积小、重量轻、可靠性高、续航能力强等特点，便于在山区、丘陵等复杂环境下布设以开展研究工作。

4 数据处理与反演方法

4.1 计算背景噪声互相关函数

数据处理基本遵循Bensen等（2007）介绍的背景噪声数据处理流程。首先进行单台数据预处理，检查连续波形的数据质量并剔除坏道，按照每一小时截取数据片段，对数据片段分别进行去均值、去线性、滤波、谱白化、时域归一化等处理。考虑到每条测线采用的地震仪器类型相同，因此我们无需去除仪器响应。然后将同一测线上所有台站两两组合，对于每一个台站对，利用对应的每小时数据片段计算互相关并叠加得到互相关函数。如图4所示，我们展示了160测线的部分互相关函数。可以看出，采集到的信号具有很高信噪比，但正负半轴的信号不完全对称，正半支信号明显强于负半支信号，这主要是噪声源分布不均匀造成的。

图4 160测线0.5~5 s周期的部分互相关函数（信噪比大于5，其中对称的红色虚线表示速度为1 km/s和4 km/s 的时距线）Fig.4 The interstation cross-correlation functions of Line 160 with the signal-to-noise ratio (SNR) greater than 5 in the 0.5-2 s period band (The red dashed lines of different slopes define the groupvelocity of 1 km/s and 4 km/s, respectively)

4.2 提取频散曲线

通过希尔伯特变换可从互相关函数中提取出经验格林函数（Yao et al., 2006）。我们采用拓距相移法对互相关函数进行处理，计算得到频散能量图并提取出相速度频散曲线。通常情况下采用正负两支相加平均的方法来压制噪声源不均匀带来的影响（Yang et al., 2007）。但考虑到线阵的互相关正、负支代表来自两个不同端源的噪声源，本文处理对正支、负支、正负支平均3种方式分别计算频散能量，为频散提取提供更多选择来避免正负支平均时有效信号被噪声湮灭。

在计算频散能量时，对于阵内相移处理，孔径设为600 m，提取周期范围为0.1~0.5 s；对于阵外相移处理，孔径设为1400 m，提取周期范围为0.2~2.0 s（图5）。比较图5a和图5d，我们可以明显发现，在中高频处（5 Hz以上）阵内相移计算得到的频散能量图质量更好，连续性更高；在中低频处（1 Hz以下）阵外相移法计算得到的频散能量图质量更好。通过对正支、负支、正负支平均3种处理方法的比较（图5a，b，c或d，e，f），可以看出，不理想的噪声源对频散能量图有明显的影响。就互相关计算出的频散能量图质量而言，正半支优于负半支的结果，这与互相关函数（图4）表现出的特征相吻合。对称叠加的结果（图5f）在1 Hz处出现间断、不连续的现象，频散能量被负半支噪声的加入干扰。在本例中，正半支互相关计算出的频散能量收敛性最好。因此，我们认为利用互相关函数的正半支、负半支、对称叠加结果分别计算频散能量是必要的，有助于我们提取更精确的频散曲线。

图5 拓距相移法频散能量图Fig.5 The dispersion energy map obtained by the extended range phase shift method

图6展示了160测线的相速度频散提取结果。阵内、阵外相移法提取的频散曲线在0.2~0.5 s频段内有一定差异（图6a），可能与阵内、阵外计算孔径不同引起的平均效应有关，但该差异仍在合理范围之内。将阵内频散和阵外频散以一定方式整合为一条宽频带频散。假设阵内和阵外频散曲线的拼接点为T拼接，在拼接点左右两侧加频率窗df，则在频率域，这个频率时间窗最左侧的频率值为最右侧的频率值为转化到时间域，这个时间窗最左侧的周期值为，最右侧的周期值为。阵内和阵外相移的平均频散曲线在0.3 s处相交（图6(a)），于是选取T拼接为0.3 s，df为0.8 Hz，则整个时间窗范围为（）。提取频散的起始周期为0.1 s，间隔周期为0.025 s，故时间窗按周期点取为（0.225 s，0.4 s）。阵内相移对于高频更加敏感而阵外相移对于低频更敏感。设置拼接点处的权重值为0.5，在拼接点左侧，阵内相移频散的权重值分别为1、0.83、0.67，阵外相移频散的权重值分别为0、0.17、0.33；在拼接点右侧，阵内相移频散的权重值分别为0.375、0.25、0.125、0，阵外相移频散的权重值分别为0.625、0.75、0.875、1。我们在该频段内将阵内频散曲线和阵外频散曲线融合，短周期以阵内频散曲线为主，长周期以阵外频散曲线为主，加权叠加得到整合后的宽频带频散曲线（图6(b)），用于反演地下介质横波速度结构。

图6 160测线相速度频散曲线Fig.6 The phase-velocity dispersion curves for Line 160

4.3 反演的初始模型和参数设置

为了得到较好的横波速度结构反演的初始模型，我们根据以下经验公式确定了初始横波速度（Xia et al., 1999）

其中μ是一个范围从0.874到0.955的常数。以相速度cR来确定深度为0.63倍波长所在层的横波速度初始值。在本文研究中，我们设置μ为0.95，以平均相速度计算出相应层的横波速度值作为初始模型。在层厚划分上，我们在深度上设置了16个薄层，各薄层层厚从地表依次向下依次为：0.1、0.1、0.2、0.2、0.2、0.2、0.2、0.3、0.3、0.3、0.5、0.5、0.5、0.5、0.5、0.5 km。反演的迭代次数设置为10次。

4.4 瑞利面波相速度的敏感核

在一维层状模型下，面波的相速度与地下介质的纵波速度α，横波波速β，密度ρ有关，在周期为ω时，相速度C在深度z方向上的敏感核可以表示为

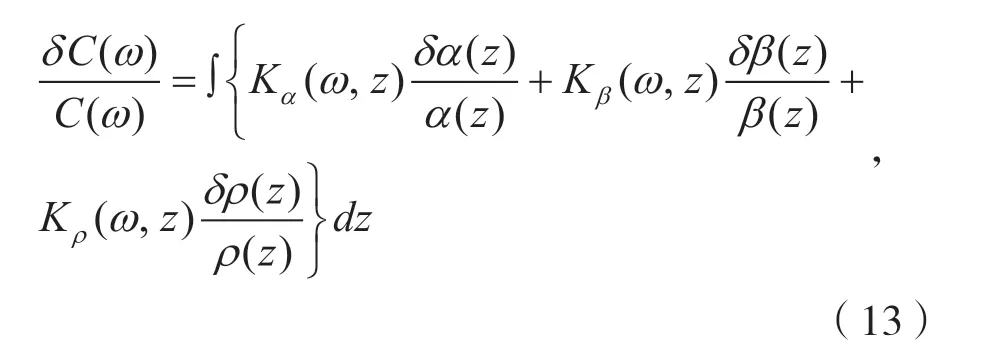
其中，Kα(ω,z)，Kβ(ω,z)，Kρ(ω,z)分别为瑞利面波相速度对纵波速度，横波速度以及密度的敏感核。

基于平均相速度的横波速度初始模型，我们计算了不同周期下瑞利面波相速度对横波速度的敏感核曲线（图7）。可见随着周期的增大，瑞利面波相速度对横波波速的敏感深度逐渐加深。在本研究中，我们选取的频散周期最大为2.0 s，可以较好地恢复2.5 km以浅的横波速度结构。

图7 不同周期（0.2 s、0.5 s、1.0 s、2.0s）下瑞利面波相速度对横波速度的敏感核曲线Fig.7 Sensitivity kernels of the Rayleigh-wave phase velocities with respect to shear-wave velocities for different periods (0.2 s,0.5 s, 1.0 s and 2.0s)

5 结果与讨论

5.1 反演结果

从反演结果可以看出，160线、360线、505线3条测线的反演横波速度结果表现出较好的一致性（图8，图9，图10），在剖面中部均存在一个低速异常体，深度达1 km左右，在剖面两侧存在高速夹层，深度在0~0.5 km，剖面由浅至深总体呈现低—中—高的速度变化。图中高程0 km代表平均海平面（MSL）。

160测线（图8）：在剖面中部、深度0.5~1 km处有一个大型低速体，测线0~4 km、深度约0.5 km处存在一个规模较大的高速体，测线5.5~8 km、深度约0.5 km处存在一高速夹层。对反演结果分析可以发现，测线中部5 km处存在一条向左倾斜的速度异常分界面，倾角约为30°，其在位置和倾向上与F1断层有着较好的对应关系。测线8.5 km处存在一条向右下延伸的速度异常带，倾角约为80°，推断此处异常是由F2断层引起的。

图8 160测线横波速度反演结果Fig.8 Vertical profile of the shear-wave velocity along Line 160

360测线（图9）：由于360测线台站稀疏，我们只利用了阵外相移中、低频频散数据进行反演，反演结果在浅地表的分辨率较低，精细结构较少。整体来看，剖面在深度0.8~1.5 km处出现高低速分界面，推断此界面为新老地层交界面。在测线5 km、深度约0.4 km处存在一个高低速夹层结构。其与左侧低速结构形成一个速度异常面，推测该处速度异常为断层F1的反映。高低速夹层沿水平方向延伸3 km左右，在测线8.5 km、深度0~0.5 km处夹层结构截断，推断此处可能存在断层。

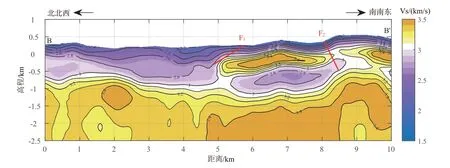
图9 360测线横波速度反演结果Fig.9 Vertical profile of the shear-wave velocity along Line 360

505测线（图10）：剖面中段呈现由浅至深地层横波速度逐渐增高、并有局部高速体凸起，反映了地下复杂的褶皱构造，剖面两端深度约0.5 km存在高速夹层。测线7.5 km的速度异常分界面与断层F2有着较好的对应关系。

图10 505测线横波速度反演结果Fig.10 Vertical profile of the shear-wave velocity along Line 505

3条剖面在深度为1.5~2.5 km处均出现一条速度分界面，此界面顶部呈隆起状，反映了此区域存在穹隆构造。3条测线剖面反演结果均出现了高低速夹层结构，这种结构很好地反映了层间褶皱和断裂。矿脉的形成明显依赖于地层岩性和构造的控制，层脉的产状与岩层基本一致。因此，我们可以通过对横波速度结构的反演来寻找断层，从而推断可能的矿脉位置。

5.2 160线背景噪声成像地质解释

根据沃溪矿区金锑钨矿成矿地质规律以及矿区坑道、钻探等已知地质资料，对160线背景噪声成像横波速度结构剖面做如下推断解释：

如图11所示，依据速度结构，剖面总体可分为上、下两大层。上层为低、中速互层结构，对应于白垩系地层和板溪群地层，该层自北西往南东厚度逐渐变薄；下层为中—高速结构，对应于冷家溪群地层和隐伏花岗岩，该层自北西往南东逐渐抬升、深度变浅。

第一大层（上层）：近地表的低速层由风化-半风化岩石及白垩系砂砾岩引起。北西段深度约0.5 km的规模较大的中速异常为板溪群五强溪组（Pt3bnw）的长石砂岩的反映，南东段深度约0.5 km的中速夹层为板溪群马底驿组上段（Pt3bnm2）砂质板岩的反映。剖面中段深度约1 km的低速层为板溪群马底驿组上段（Pt3bnm2）泥质板岩的反映。上层底部的中等速度层为板溪群马底驿组下段（Pt3bnm1）变质砂岩的反映，断层F2东南侧的低—中速层状体与冷家溪群（Pt2lj）绢云母板岩对应。

剖面左侧2 km处存在一条速度异常带，推断该异常为断层F4的反映，其上盘为新地层白垩系砂砾岩,下盘为老地层五强溪组，因此断层F4为正断层。剖面中段5 km处，存在一条倾角为30°的速度分界面，其与断层F1有着较好的对应关系。

剖面中段5 km附近、F1下盘，马底驿组上段（Pt3bnm2）泥质板岩与其上、下较高速度层的过渡上分布有矿脉V7、V8（图11 黄色线）。根据此特征推断V7、V8矿脉（图11 黄色虚线）可能沿此两个高低速过渡带左右延伸，F1下盘的这两个高低速过渡带是上沃溪至龚家湾深部找矿的有利部位。

第二大层（下层）：该层顶界面呈波状起伏，总体自西北往东南逐渐抬升，它反映了该地段老地层隆起，与本区存在穹窿构造的已知地质实事吻合；顶界面存在3处明显的局部凹陷，系区域性断裂切割深部地层所致。该层内分布有两个明显的高速异常体，据区域地质资料推断两高速体为隐伏的花岗岩体。

据剖面内存在自浅至深延伸的低速带、速度界面不连续、速度层厚度或产状发生突变等特征，推断F1、F2、F4等3条区域性断层，其中F1是本区的控矿导矿构造。

6 结论

本文介绍了一种面波勘探的数据处理新方法——拓距相移法。该方法将传统相移法与背景噪声互相关相结合，很大程度上改善了传统相移法在低频段频散信号提取较差的问题，有效地拓宽了提取频散的可用频带，使横波速度反演在不降低浅层分辨率的前提下提高了对深部结构的有力约束。我们将拓距相移法应用于湖南沃溪金锑钨矿区采集的背景噪声数据，通过阵内相移和阵外相移分别提取了中高频和中低频的频散曲线，将不同阵列得到的重叠频率域的频散曲线进行加权叠加，得到了0.1~2.0 s的频散曲线，并将该频散曲线用于反演，从而获得了高分辨率的中浅层地下横波速度结构。通过利用已有的地质资料进行对比验证以及进一步的地质解释，我们发现160测线的地震横波速度反演结果与断层、岩性分界面及矿脉有着较好的对应关系。本文的研究为今后深部找矿提供了一种有效的高精度成像方法。