Coupled flow and heat transfer of power-law nanofluids on non-isothermal rough rotary disk subjected to magnetic field

2022-06-29YunXianPei裴云仙XueLanZhang张雪岚LianCunZheng郑连存andXinZiWang王鑫子

Chinese Physics B 2022年6期

Yun-Xian Pei(裴云仙), Xue-Lan Zhang(张雪岚), Lian-Cun Zheng(郑连存), and Xin-Zi Wang(王鑫子)

School of Mathematics and Sciences,University of Science and Technology,Beijing 100083,China

Keywords: power-law nanofluids,magnetic field,improved BVP4C algorithm,rough rotating disk

1. Introduction

The fluid flow and heat transfer on a rotating disk is a common phenomenon in life.It involves many aspects such as rotating heat exchangers,[1]disk drives, atomizers, food processing,and medical services,[2]etc.For half a century,many researchers[3–7]have devoted themselves to studying the flow and heat transfer on the rotating disk. Von K´arm´an[8]discussed the “free disk” problem by assuming it to be axisymmetric and introducing similar transformations. The results show that the circumferential velocity of the fluid increases as the distance from the rotation axis of the disk increases.Cochran and Goldstein[9]conducted the numerical integration to obtain the axial and radial velocity distribution of the fluid in the“free disk”problem based on the similarity transformation proposed by Von K´arm´an.

Enhancing heat transfer has become an essential demand today,and the active and passive technologies are the two ways to achieve the above goals. The passive technologies such as special geometries, fluid additives, and hot filling are more popular nowadays. The active technologies include magnetic and electric fields.[10]The passive technologies have become important methods in various fields, and relative researches have been carried out as can be found in Refs. [11–13] and others. Wanget al.[14]used the main factors of temperature deviation to study the transport of steady-state heat flow.Based on the development of experimental and theoretical researches,it is generally believed that surface discontinuity can improve heat transfer. Periodic discontinuous surfaces can make the thermal boundary layer thinner, thereby improving heat transfer efficiency.[2]Out of this reason, many scholars used periodic surface roughness to study fluid flow and heat transfer. Le Palec[15]and Le Palecet al.[16]conducted experimental and theoretical researches by using sinusoidal curve to simulate roughness, and analyzed the heat transfer mechanism of fluids on the rough rotating disk. Yoonet al.[17]studied the fluid flow on a sine-shaped rough infinite surface,they found that the torque coefficient and the Nusselt number are positively related to the surface roughness. The thermal boundary condition that the free rotating disk wall exhibits a power-law distribution has been studied by Dorfman and Serazetdinov[18]and Shevchuk.[19]The studies of the uneven temperature distribution on the rough rotating disk can be obtained from Refs. [2,20]. In the two articles the non-uniform temperature distribution of the radius power-law is used. The above researches illustrate the influence of passive technology on heat transfer.

The application of active technologies-magnetic and electric fields to changing the flow and improving the heat transfer has always been a hot research topic. Luet al.[21]studied the effect of anisotropy on the magnetoacoustic response of a magnetoacoustic surface wave resonator. Quet al.[22]carried out a study of the electrical properties of Ca3Co4O9+δ(CCO)materials prepared under a magnetic field. The presence of a magnetic field significantly improved the texture, grain size,and density of the material, thereby increasing the conductivity. Hayat and Nadeem[23]introduced the effect of buoyancy on the flow of incompressible, viscous, and conductive nanofluids at the stagnation point of magnetohydrodynamics on a vertically stretched sheet, by taking into account the effects of induced magnetic fields and viscous dissipation. Liet al.[24]studied the propagation of magnetic nanotube domain walls driven by a magnetic field,and the role played by magnetic field in accelerating the motion. Attia and Aboul-Hassan[25]studied the effect of an external uniform magnetic field on the flow caused by a rotating disk, showed that the Hall effect has an influence on the velocity component. Ushaet al.[26]studied and solved the problem about the loss of thin conductive liquid film on rough surface caused by centrifugation,and found that the existence of magnetic field further enhances the retention of liquid film on rotating disk. The effect of magnetic field on fluid flow on rough rotating wave disk has not been reported in the existing literature.

The traditional heat exchange rate medium has low thermal conductivity, which can no longer meet the increasing requirements for heat exchange in industrial engineering. Nanofluid is a mixture of base fluid and nanoparticles and has good thermal performance,[27]which is often used in drag reduction refrigeration (such as household refrigerators and coolers), boiler exhaust gas recovery, and heat storage,etc.[28]Li and Cao[29]combined the Boltzmann transport equation(BTE)equation and solid isotropic material with penalization (SIMP) method to develop a topology optimization method for ballistic diffusion heat conduction. Wanget al.[30]revealed the scaling behavior of the thermal conductivity ofα-Fe2O3nanowires and analyzed the thermal conductivity of nanomaterials. Xiet al.[31]proposed a formula that is generally applicable to the calculation of thermal conductivity of liquids and amorphous solids. Wanget al.[32]studied the Leidenfrost effect on the nanoscale,which is helpful in designing the anti-drag surface,self-propelled droplets,and selfassembled nanostructures,and also conducive to other relevant applications. More nano-related researches can be found in Refs.[33–37]and other papers. Mehmood and Iqbal[38]studied the effects of heat absorption and nanoparticles on natural convection heat transfer along the vertical wave cone,showing that the heat transfer rate and friction coefficient are positively related to the volume fraction.

The study of non-Newtonian fluids on rotating disk has always been a hot research topic due to the complexity of its research and the wide range of applications. Alqarniet al.[39]used Carreau model to study the instability of non-Newtonian boundary layer flow on a rough rotating disk. Researchers’enthusiasm for studying power-law fluids has not diminished in the studies of many non-Newtonian fluids. Anderssonet al.[26]modeled the power-law fluid flow caused by a rotating disk. He proposed a reliable numerical calculation method,which can also accurately calculate the shear thickened fluid.Minget al.[40]studied the steady-state flow and thermal effects of fluids on the assumption that the viscosity and thermal conductivity obey power-law characteristics. The most recent researches on the flow of power-law fluids on rotating disks can be found in Refs. [41,42]. Existing studies have shown that little attention has been paid to the power-law fluids on the rough non-isothermal wave disk.

As mentioned above, the Newtonian fluid flow and heat transfer on non-isothermal rough rotating disk have been studied,but the non-Newtonian power-law nanofluid have not been investigated yet. In the present work,we study the power-law Nanofluids on a non-isothermal rough rotary disk subjected to a magnetic field. The problem is formulated,and an improved BVP4C algorithm is proposed to solve nonlinear partial differential equations. The influences of volume fraction,types and shapes of nanoparticles, magnetic field and power-law index on the flow and heat transfer behavior are analyzed.

2. Formulation of problem

We introduce the orthogonal coordinate system(x,θ,y),[2]wherexrepresents the direction of the wave surface of the disk,ydenotes the direction perpendicular to the surface, and the azimuth direction is indicated byθ. A magnetic field with an angle ofΩand a magnitude ofBis applied to the surface of the disk, where the formulaa0/λcontrols the surface morphology of the disk, which is the ratio of amplitude to wavelength. To avoid flow separation and make the control system effective, the boundary layer thickness should be much smaller than the wavelength (i.e. δ ≪λ) under the same levela0/λ ≤0.2.[16]In this work, 0.4%CMC aqueous solution is chosen and used as the base fluid to study the uniform distribution of nanoparticles(e.g.,Al2O3,Cu,Ag)in the base fluid. The viscosity coefficient of the nanofluidμcan be obtained from the following formula:

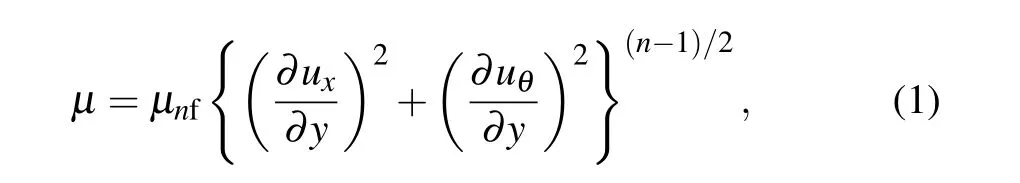
wherenis the power-law exponent. Especially whenn=1,it is Newtonian fluid,n ＜1 it is plastic fluid[43]andn ＞1 it is dilatant fluid.

Fig.1. Schematic diagram of physical model.

Based on the above descriptions, we formulate the governing equations as follows:

whereσis the magnetic permeability,u=(ux,uy,uθ) represents the relevant velocity vector.

3. Solution procedure

3.1. Similarity transformation

Owing to the setting of the rough disk surface function,dr/dxcan be defined as According to Ref.[20],dimensionless variables and flow functions are defined as follows:

The corresponding dimensionless boundary conditions are

Table 1. Different properties of nanoparticles and base fluid (CMC–H2O).[47,48]

Owing to the radial flow and the azimuthal flow,the shear force along the direction of the curve and the direction of the azimuth angle are written,respectively,as

whereqis the wall heat flux,ReΛrepresents the rotational Reynolds number, andνis the dynamic viscosity coefficient of fluid.

Le Palec[15]has shown that taking the area of the flat disk as a reference, we can increase Nusselt number of the wave disk by increasing the area ratioS/πb2(Srefers to the wavy disk area), thereby increasing the heat transfer. The expressions of Nusselt numbers (average and modified) can be derived as follows:

3.2. Method solving

In Ref.[2],Mehmoodet al. used the Keller–Box method to solve two-dimensional nonlinear partial differential equations. The Keller–Box method needs to difference between two independent variables, and uses the chasing method to solve the matrix equation according to the Newton iteration method,which is labor-intensive and time-consuming.

The existing BVP4C algorithm can be used only to solve one-dimensional differential equations.However,in this work,we formulate the two-dimensional nonlinear partial differential equations. In order to solve these equations here,we introduce the idea of difference to transform the two-dimensional variable into the equations with derivatives with respect to only one variable,so that the existing BVP4C algorithm can be used to solve the equations. This improved method gets rid of the limitations of BVP4C.In this work,the improved BVP4C algorithm is used to solve the formulated equations and the obtained solutions are compared with the numerical solutions in the literature, thereby verifying their good consistence and the effectiveness of the method(see Table 2).

Table 2. Comparison between numerical simulation results from two algorithms.

3.3. Algorithm solution steps

According to the improved BVP4C algorithm idea, we need to difference one of the two-dimensional variables. For the variablesεandηin the two directions,we choose the difference operation on the derivative in theεdirection. Letdbe the step size in the direction, the derivatives of functionsf(ε,η),Φ(ε,η),andΘ(ε,η)in theεdirection are subjected to difference operation, wherenis the position of the node during the difference operation. Simplifying Eqs. (14)–(16)by difference yields the following equations:

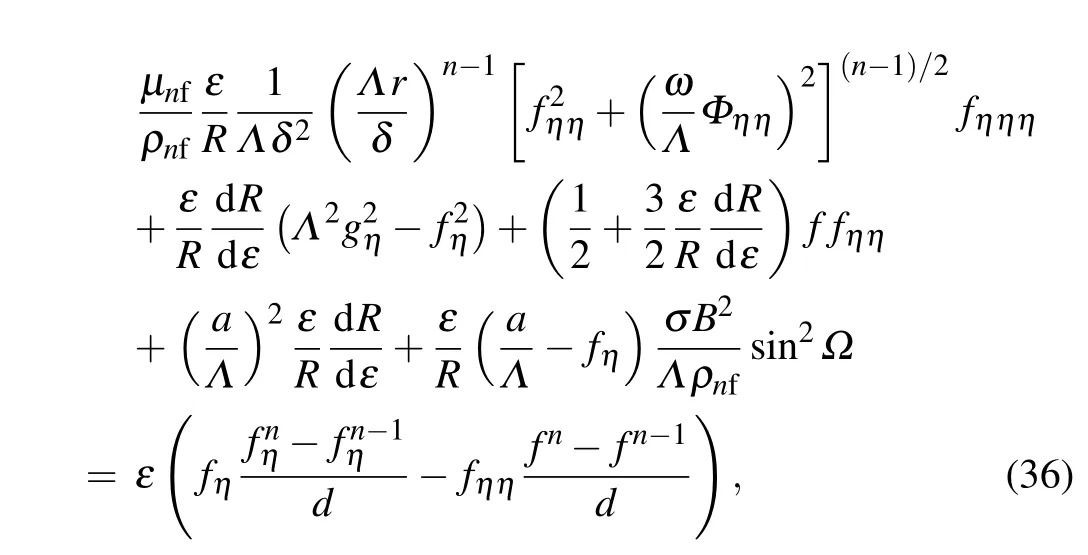
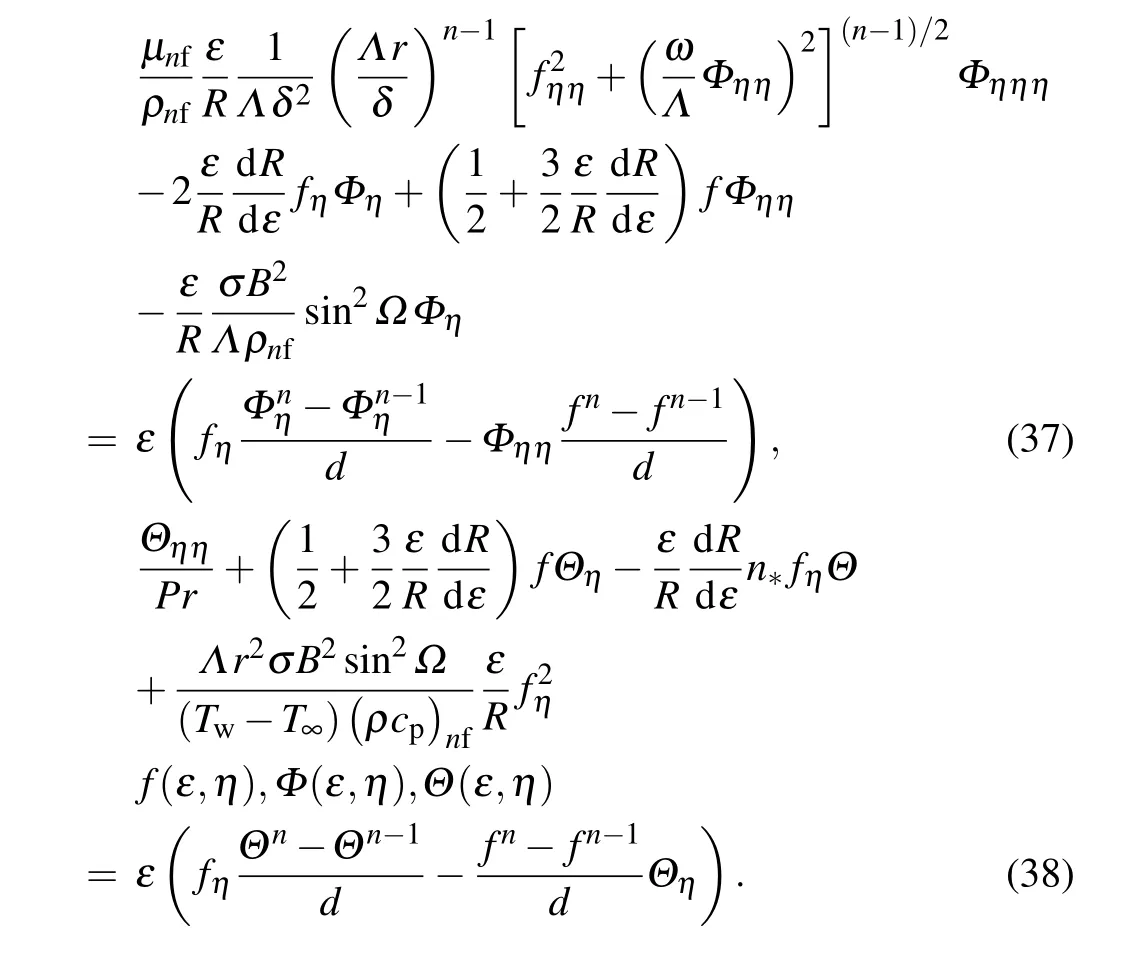
4. Results and discussion

Now, we solve Eqs. (14)–(16) with boundary conditions Eqs. (17) and (18) by our improved BVP4C algorithm. The numerical results are shown and analyzed in the following.

Figures 2(a)–2(d) show for each fixed power-law indexn(n=0.5, 1, and 1.2, shear thinning, Newtonian fluid and shear thickening),the effects of nanoparticle volume fractions(0%, 1%, 2%, 4%)on velocity field. It is found that for each fixednand different values of nanoparticle volume fraction(NVF)Φ, the velocity profiles are almost overlapped, which means that the volume fraction has almost no effect on velocity field. However,we see that the azimuthal velocity changes remarkably with the value ofn, which can also be seen from Fig. 3. By taking the peak velocity value in the azimuth direction when the volume fraction is 4% in Figs. 2(b)–2(d), it can be seen that the difference is very small, indicating that the volume fraction has almost no effect on the velocity in this direction. Figures 2(c)and 2(d)show that under the influence of nanometer volume fraction and power-law exponent,the power-law exponent has a greater influence on axial velocity. In the three representative different nanofluid types, the images have more obvious differences. The larger the volume fraction,the smaller the azimuthal friction coefficient between fluid molecules is(see Fig.5),which promotes fluid flow but the effect is insignificant.

Figures 3(a) and 3(b) illustrate the effects of power-law exponents (PLEs) (n= 0.3, 0.5, 1, 1.2, and 1.5) on velocity field. The results show the PLE has almost no effect on the velocity in thexdirection (Fig. 3(a)). However, it has very remarkable effect on the velocity profile inθdirection(Fig.3(b)). The increase of the power-law exponent will lead the axial shear force to increase,which in turn affects the axial velocity of the fluid. The thickness of the fluid dynamic boundary layer becomes thinner with the increase of PLE,and the azimuth velocity is greatly affected by the thickness. The change in flow rate occurs significantly in the axial direction to supplement the radial outflow.

Fig.2. Effects of different volume fractions on velocities for Al2O3/CMC nanofluid.

Fig.3. Effects of different PLEs on velocities for Al2O3/CMC nanofluid.

Figures 4(a)–4(d) reveal the effects of magnetic field inclination angle on the velocity profile both in thexdirection and in theθdirection for fixed power-law indexn. It can be seen that the angleΩhas almost no effect onux,but has very strong influence onuθ. For each fixed value ofn, the velocity profileuθdecreases as the inclination angleΩincreases.From Figs.4(b)–4(d)for the four different inclination angles,the peak value ofuθis present whenΩ=π/6 and the velocity profile of plastic fluid is higher than the other three ones. The greater the inclination angle of the magnetic field,the stronger the effect of the Lorentz force on the surface of the fluid is,which slows down the flow of the fluid. For the azimuth direction velocity,the wall shear stress decreases with the magnetic field angle increasing.

Fig.4. Effects of different magnetic field inclinations on velocity for Al2O3/CMC nanofluid.

Fig.5. Variations of local Nusselt number and friction coefficients with nanoparticle volume fraction value(Al2O3/CMC nanofluid,Pr=0.71,n*=2,n=2).

Table 3. Values of under different volume fractions and shape factors.

Fig.6. Variations of local Nusselt number and friction coefficients with type of nanoparticles(Pr=0.71,n*=2,n=2).

Fig. 7. Variations of local Nusselt number with nanoparticle type for Al2O3/CMC nanofluid(Pr=0.71,n*=2,n=2).

Fig.8. Variations of local Nusselt number and friction coefficients under different values of magnetic field strength(Al2O3/CMC nanofluid,Pr=0.71,n*=2,n=2).

Fig. 9. Variations of local Nusselt number and friction coefficients under different value of magnetic field angle (Al2O3/CMC nanofluid,Pr=0.71,n*=2,n=2).