Local sum uncertainty relations for angular momentum operators of bipartite permutation symmetric systems

I Reena H S Karthik J Prabhu Tej Sudha A R Usha Devi and A K Rajagopal

1Department of Physics,Jnanabharathi,Bangalore University,Bangalore-560056,India

2International Centre for Theory of Quantum Technologies,University of Gdansk,Gdansk,80-308,Poland

3Department of Physics,Ramaiah University of Applied Sciences,Bangalore-560054,India

4Department of Physics,Kuvempu University,Shankaraghatta,Shimoga-577 451,India

5Inspire Institute Inc.,Alexandria,Virginia,22303,USA

Keywords: sum uncertainty relations,permutation symmetry,rotational invariance

1. Introduction

Uncertainty relations place fundamental limits on the precision achievable in measuring non-commuting observables.The original idea of uncertainty relation was first introduced by Heisenberg[1]for position and momentum observablesQ,P.Subsequently,Kennard[2]formulated a mathematically precise version(with ¯h=1)

which is commonly referred to as the Heisenberg–Robertson uncertainty relation in the literature. Here [A1,A2]=A1A2-A2A1denotes the commutator of the observablesA1andA2.The uncertainty relation(2)imposes restrictions on the product of variances(ΔA1)2and(ΔA2)2,essentially limiting the capability towards precise prediction of the measurement results of non-commuting observables. In general, the Heisenberg–Robertson approach of placing limits on the uncertainties of incompatible observables in the given quantum stateρsets the conventional framework for deriving preparation uncertainty relations.(Preparation uncertainty relations place intrinsic bounds on the spread of incompatible observables, measured in different statistical trials,using identical preparations of a quantum state. On the other hand, measurement uncertainty relations impose bounds on the error occurring in the measurement scheme of one of the observables and the corresponding post-measurement disturbance caused on the other observable in an apparatus.)[5]

Apart from their fundamental interest, uncertainty relations play a significant role in the field of quantum information processing, with several applications such as entanglement detection,[6–8]quantum cryptography,[9–15]quantum metrology[16]and foundational tests of quantum theory.[16,17]Motivated by their applicability, there has been an ongoing interest in reformulating uncertainty relations expressing trade-off of more than two incompatible observables,formalized in terms of variances,[6,8,18–32]or via information entropies.[33–42]Recently several experimental tests have been carried out to verify different forms of uncertainty relations.[43–46]

In this paper,we investigate variance based local sum uncertainty relation(LSUR)for local angular momentum operators of a bipartite quantum system,proposed by Hofmann and Takeuchi,[6]and examine the implications of its violation in bipartite permutation symmetric systems. We show that the angular momentum LSUR, which places lower bound on the set of all bipartite separable states, gets violated if and only if the covariance matrix of the two-qubit reduced system of theN-qubit permutation symmetric state is not positive semidefinite. Since it has been shown[47–49]that the covariance matrix negativity serves as a necessary and sufficient condition for entanglement in a two-qubit symmetric system, our result establishes a one-to-one connection between violation of the LSUR and pairwise entanglement.

2. Sum uncertainty relation

It may be noted that the term〈[A1,A2]〉=Tr(ρ[A1,A2])appearing on the right-hand side of the Heisenberg–Robertson uncertainty relation (2) vanishes in some specific quantum statesρ. In such cases, one ends up with a trivial relation (ΔA1)2(ΔA2)2≥0 for the product of variances of noncommuting observablesA1,A2. Moreover, variance vanishes in the eigenstate of one of the observables. In such cases the Heisenberg–Robertson uncertainty relation(2)fails to capture the intrinsic indeterminacy of non-commuting observables.To overcome such issues it is preferable to employ uncertainty relations placing non-trivial bounds on the sum of variances(ΔA1)2+(ΔA2)2. In fact, a lower bound for the sum of variances may be found by using the inequality ∑mα=1aα/m ≥(∏α aα)1/mbetween the arithmetic mean and the geometric mean of real non-negative numbersaα,α= 1,2,...,m.Choosinga1=(ΔA1)2, a2=(ΔA2)2and using relation(2)one can obtain a variance based sum uncertainty relation

However,the sum uncertainty relation(3)is a byproduct of the Heisenberg–Robertson inequality(2)and thus it is noninformative for some quantum statesρ, in which one of the variances and/or〈[A1,A2]〉vanish.

2.1. Sum uncertainty relations for angular momentum operators

Hofmann and Takeuchi[6]proposed that a non-trivial lower boundU ＞0 must exist for the sum of variances∑α(ΔAα)2of a set{Aα},α=1,2,...of non-commuting observables, as they do not share any simultaneous eigenstate,i.e., for non-commuting observables{Aα},α=1,2,..., the following inequality holds good:[6]

Thus, one obtains a variance based sum uncertainty relation for the components (J1,J2,J3) of angular momentum operator:[6]

2.2. Local sum uncertainty relations for bipartite systems

Let us consider angular momentum operatorsJAα, JBαacting on the Hilbert spacesℋA,ℋBof dimensionsdA=(2jA+1),dB=(2jB+1) respectively. They satisfy the sum uncertainty relations by performing measurements on the other subsystemB. More specifically,violation of LSUR signifies in general that correlations between subsystems in an entangled state can be determined with enhanced precision than those in a separable state.

It is of interest to explore if violation of local sum uncertainty relations is both necessary and sufficient to detect entanglement in some special classes of bipartite quantum systems.To this end,Hoffmann and Takeuchi[6]considered the following two-qubit LSUR:

in the Werner class of two-qubit states, which are known to be entangled forx ＞1/3. From Eq.(12)it is evident that the LSUR (10) is violated in the parameter range 1/3＜x ≤1.Thus,violation of the two-qubit LSUR(10)is both necessary and sufficient for detecting entanglement in the one-parameter family of two-qubit Werner states.

In the next section we discuss violation of LSUR in permutation symmetricN-qubit states.

3. Violation of LSUR by permutation symmetric N-qubit states

Our main result is presented in the form of the following theorem.

Theorem 1 Permutation symmetric evenN-qubit state violates the angular momentum LSUR (29) if the associated two-qubit covariance matrixC=T-ssThas a strictly negative eigenvalue.

Proof Violation of the LSUR (29) is ensured whenever there exist axis-angle parametersa=(a1,a2,a3)T,aTa=a21+a22+a23=1,0≤θ ≤2πsuch thatχ(ˆa,θ)＜0.We show in the following that it is possible to choose these parameters such thatχ(ˆa,θ)＜0 ensuring violation of LSUR (29) when the two-qubit covariance matrixC=T-ssTis not positivedefinite possessing at least one negative eigenvalue.

Substituting the explicit form[59]for the elements of the rotation matrixR(ˆa,θ),i.e.,

where LSUR (29) is expressed in terms of the least eigenvalue of the two-qubit covariance matrixC. As long ascL≥0(which happens to be the case for separable symmetric states)the LSUR(39)is obeyed.

We discuss two specific physical examples ofN-qubit symmetric states which violate relation (39) in the following section.

4. Examples of N-qubit symmetric states violating the angular momentum LSUR

4.1. Symmetric multiqubit state generated by one-axis twisting Hamiltonian

Kitagawa and Ueda[60]proposed a nonlinear Hamiltonian

We then construct the covariance matrixC=T-ssTand evaluate its eigenvalues as a function of the number of qubitsNand the dimensionless dynamical parameterχt. Figure 1 illustrates the behavior of the left-hand side of the LSUR (39)with respect toχtfor different choices ofn=N/2. Violation of LSUR (39) is clearly seen in Fig. 1, as 1+ncL＜1 and it is a signature of entanglement in the symmetricN-qubit state(40),where bipartite divisions are characterized by the collective angular momentajA=jB=n/2.

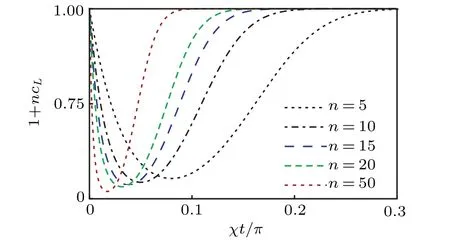
Fig.1. A plot of(1+ncL),the left-hand side of the LSUR(39),in the N-qubit symmetric state|ΨKU〉given in Eq.(40),as a function of the dimensionless dynamical parameter χt for different choices of n=N/2.

4.2. One-parameter family of W-class N-qubit states

We consider the one-parameterN-qubit symmetric state of the W-class:[61]

We have plotted the left-hand side of the LSUR(39)as a function of the parametera, for different choices of the angular momentajA=jB=n/2 in Fig.2. Violation of the LSUR,i.e.,(1+ncL)≤1, is manifestly seen in Fig. 2, revealing entanglement in the bipartite divisions (characterized by collective angular momentajA=jB=n/2)of the W-classN-qubit state(43).

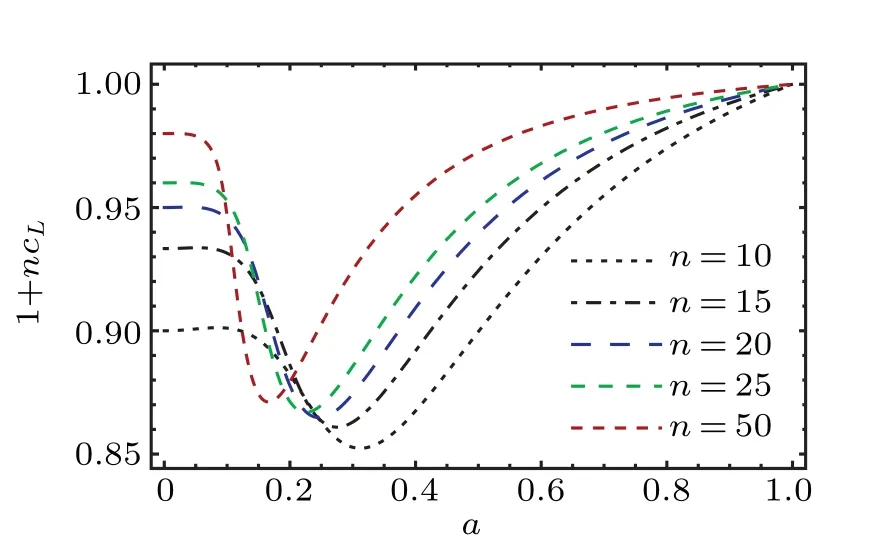
Fig.2. Plot of(1+ncL), i.e., the left-hand side of relation(39)of the LSUR,in the W-class N-qubit symmetric state(43),as a function of the parameter a for different values of n=N/2. Here cL denotes the minimum eigenvalue of the covariance matrix C (see Eq. (47)) associated with the W-class state.

5. Concluding remarks

In this paper, we have shown that angular momentum LSUR in bipartitions of symmetric multiqubit states with even number of qubits are violated when the covariance matrix of the two-qubit subsystem is not positive-definite.Entanglement between equal bipartitions is ensured when the LSUR in angular momentum operators of an evenN-qubit symmetric state is violated or equivalently the covariance matrix of the two-qubit subsystem possesses at least one negative eigenvalue. Our illustration of this result in two important classes of symmetric multiqubit states helps in discerning entanglement in their equal bipartitions through the parameters of two-qubit reduced system.

One of the main advantages of employing LSUR is the fact that it is possible to detect entanglement without a complete knowledge of the quantum state and it suffices to determine experimental friendly variances of local angular momentum observables for this purpose. As violation of LSUR is a collective feature of entanglement in symmetric multiqubit states,it is of interest to contrast this with another experimental friendly feature namely,spin squeezing.[62,63]Spin squeezing is only a sufficient collective criterion for pairwise (twoqubit) entanglement in multiqubit symmetric states. Not all entangled symmetric states are spin squeezed. On the other hand, violation of LSUR reflects itself as a collective feature which is both necessary and sufficient for pairwise entanglement. A promising future direction lies in formulating LSUR for higher rank irreducible tensors constructed from angular momentum operators[64]so that their violation brings forth genuine entanglement beyond two-qubit quantum correlations in the global symmetric system.

Acknowledgements

HSK acknowledges the support of NCN,SHENG(Grant No. 2018/30/Q/ST2/00625). IR, Sudha and ARU are supported by the Department of Science and Technology, India(Grant No.DST/ICPS/QUST/Theme-2/2019).