Ultrafast plasmon dynamics in asymmetric gold nanodimers

Bereket Dalga Dana Alemayehu Nana Koya Xiaowei Song(宋晓伟) and Jingquan Lin(林景全)

1School of Science,Changchun University of Science and Technology,Changchun 130022,China

2Department of Physics,College of Natural and Computational Sciences,Wolaita Sodo University,P.O.Box 138,Wlaita Sodo,Ethiopia

Keywords: ultrafast plasmon dynamics,coherent control,spectral intensity,temporal maximum

1. Introduction

Surface plasmon resonance (SPR) is a collective oscillation of conduction band electrons that is induced by externally applied optical fields on nanoparticles. It is associated with intense local field confinement and extraordinary intensity enhancement, which are crucial for a multitude of applications in optical sensing, enhanced spectroscopy and photocatalysis.[1–3]The resonant frequency of SPR can be controlled by changing the geometry and morphology of plasmonic nanostructures, implying their potentials for applications in a wide range of electromagnetic spectrum.[4]Varying the aforementioned parameters is a common way to control the plasmon resonance and collective optical properties of coupled nanosystems.[5]In particular,the enhanced optical response associated with SPR offers an opportunity to investigate their ultrafast plasmon dynamics of local fields by detecting their time-resolved optical response with ultrafast laser techniques.[6]

Understanding the ultrafast dynamics of localized surface plasmon resonances (LSPRs) in asymmetric dimers is essential to the understanding of the fundamental physics of lowdimensional materials.[7]However, monitoring ultrafast plasmon dynamics is a challenging task so it has received much attention from the ultrafast nanophotonics community.[8]Hence,the study of ultrafast dynamics of LSPRs is crucial not merely for better comprehending the fundamental physics but also for emerging plasmon-based applications.[9]Symmetry breaking in homodimers via geometry and morphology offers a new opportunity to control the optical properties of coupled nanosystems at the femtosecond timescale.[10,11]The recent experimental and theoretical studies on the temporal dynamics of symmetric dimers[12–14]suggest that exploring the ultrafast temporal dynamics of asymmetric nanodimers would be of great interest[15]and requires further insight. Most recent studies in this field have focused on the effect of symmetry breaking in plasmonic nanoparticles on the spectral features of local fields[16,17]and elucidated that the effect of sizeasymmetry on ultrafast plasmon dynamics thorough the broken symmetry plays an important role in many plasmon-based applications.However,the effect of symmetry breaking on the ultrafast plasmon responses of Au nanodisk dimer by varying the diameter of one of the constituent nanodisks has not been well understood.Thus,theoretical investigation of the ultrafast plasmon dynamics of size-asymmetric plasmonic nanodimers is highly needed. In particular, the coherent control of ultrafast plasmon dynamics of size-asymmetric plasmonic nanodimers because of varying the time and phase delays of the ultra-short laser pulses has not been studied. Furthermore,a thorough comprehension of ultrafast plasmon responses of asymmetric dimers excited by double pulsed fields is crucial for experimental studies[18]and practical applications.

To this end, we theoretically investigate the ultrafast plasmon responses of constantly morphed symmetric Au ND dimer into size-asymmetric Au ND dimers using single-pulse excitation. The ultrafast plasmon responses of Au ND dimer by controlling the diameter of one nanodisk while fixing the geometry of the other were first studied here. We show a single broad spectral peak and three spectral peaks for symmetric and size-asymmetric dimers, respectively. We observed that the symmetric dimer shows at most, one temporal maximum and no beats in ultrafast temporal dynamics,whereas a size-asymmetric dimer has three temporal maximum and two beats. Moreover,we have found striking differences in the ultrafast temporal dynamics between both systems. The shape of temporal dynamics of the size-asymmetric dimer is significantly deformed due to the excitation of local plasmon modes with different wavelength components. Furthermore, the decay time of the amplitude of the local field is longer and oscillates with a higher frequency due to the narrower linewidth and red-shifted spectral peaks. Secondly,we have studied the coherent control of the ultrafast plasmon dynamics of sizeasymmetric Au ND dimer as a function of the time and phase delays of the excitation pulses. By using double-pulse excitation, it is found that the ultrafast plasmon dynamics of symmetric Au ND and size-asymmetric Au ND dimers display a substantial modification in their ultrafast plasmon dynamics of local fields. The results were interpreted with the help of the concepts of coherent superposition and a plasmon hybridization model. Our study would open new paths to understanding ultrafast plasmon responses in size-asymmetric nanodimers to design nanosystems with appropriate properties for different applications and to observe their rich optical responses.

2. Model and method

The studied nanosystems are comprised of equal size of NDs with diameterD1=D2=100 nm,thicknessH=50 nm and gapg= 10 nm for symmetric Au ND dimer and unequal size of NDs withD1=100 nm,D2=100 nm–160 nm,H=50 nm andg=10 nm for the size-asymmetric Au ND dimer which are schematically shown in Fig.1. First,we used symmetric Au ND dimer,to explore the influence of symmetry breaking on the ultrafast plasmon responses by changing the diameter of ND2 from 100 nm to 160 nm while a fixed geometry of ND1 excited by a single ultra-short laser pulse. The ultrafast temporal dynamics being simply the Fourier transform of the spectral response. Currently,broadband lasers that are proficient in delivering 15 fs pulse are used by numerous research groups for the study of ultrafast dynamics in a large variety of systems.[19]Both the dipole and quadrupole modes can be exited simultaneously by this pulse.[20]To exploit these potentials of the state-of-the-art ultrafast lasers,we employed ultra-short laser pulse with a pulse duration ofτ=15 fs and central wavelengthλ=800 nm. As shown in Fig.1,the symmetric and size-asymmetric dimers are placed on the SiO2substrate with a thickness of 50 nm and its dielectric constant is taken from Ref.[21]. This nanosystem is irradiated by a single ultrafast laser pulse,which is injected along thez-axis,perpendicular to the plane of the nanostructures,and the ultrafast laser pulse is illuminated by the entire nanosystem as shown in Fig.1(f).

Next,the coherent control of ultrafast plasmon dynamics of both symmetric Au ND and size-asymmetric Au ND dimers are studied as a function of the temporal and phase delays of the pulses with identical pulse durations and a central wavelength as shown in Fig. 1. Here, we used a couple of ultrashort laser pulses with well-controlled inter-pulse delay timetDand phase shift Δφ(see Fig.1(g)). To interpret our numerical results, we used the concept of superposition principles.As the two ultra-short pulses of equal time-varying envelope function and frequency travel together in the same direction,the resulting field intensityIR(t)of such fields is obtained by using the principle of superposition[13,22]

wherecis the speed of light in empty space,ε0is the permittivity of the free space,tD=t2-t1is the time delay and Δφ=φ2-φ1is the relative phase shift between the two ultrafast laser pulses.

For a fixed fundamental frequency or wavelength,the resulting intensityIR(t)has a maximum value at zero time and phase delays between two pulses, as we observed in Eq. (1).Similarly,the resultant intensity has the least value if the temporal delay between the excitation pulses sets maximum with a steady phase shift.[13]Hence, the ultrafast plasmon dynamics of coupled nanosystems can be influenced by monitoring the time delay(tD)and phase delay(Δφ)of the two pulses.[13]To prove our expectations, we used Au ND homodimer in Fig. 1(a) and the size-asymmetric Au ND dimer in Fig. 1(e)which supports strongly enhanced and confined electromagnetic fields. To study the effect of time delay and the relative phase of a pair of delayed ultrafast pulses on the ultrafast plasmon dynamics of the two systems, we used double ultrafast pulses each having the same pulse duration and central wavelength but different relative phases and offset times.

The spectral features and ultrafast temporal dynamics of symmetric Au ND and size-asymmetric Au ND dimers were studied using FDTD simulations. By using this method,Maxwell’s equations in the time domain are solved to study the ultrafast dynamics of the local electric fields.[23]We recorded the ultrafast plasmon responses of both systems by using a time-domain monitor set at the mid-point of the systems. The spatial and surface charge distributions at constant wavelength were calculated by a power monitor placed 2 nm above the nanosystems. The dielectric functions of the studied symmetric Au ND and size-asymmetric Au ND dimers were modeled using the experimental data of Johnson and Christy.[24]To confirm the accuracy of the results, the three-dimensional mesh in the calculations had a unit size of 1.25 nm×1.25 nm×1.25 nm within the gap-region of both symmetric and sizeasymmetric dimers and up to 2 nm×2 nm×2 nm otherwise.Perfectly matched layer boundaries were applied along the edges of the simulation region. The convergence test of the calculation has been carried out and the results presented in the current study show that the error was within the acceptable limit.[16]Our results were interpreted by using the concepts of the plasmon hybridization model.[25]

Fig.1.Panel(a)shows how the symmetric Au ND dimer consists of two NDs with equal diameters. Asymmetry is introduced into the system by varying the diameter of ND2 as shown in (b)–(e). The height of the NDs and the dimer gap were set to be H =50 nm and g=10 nm,respectively. To probe the influence of symmetry breaking on ultrafast plasmon responses,symmetric Au ND dimer was excited by a single linearly polarized ultrafast pulse,which is illuminated along the z-axis(see(f)). To study the coherent control of ultrafast plasmon responses, the size-asymmetric Au ND dimer was excited by the ultrafast laser pulses, which are irradiated along the z-axis (K1 and K2),having finite time delay(tD)and the relative phase difference(Δφ)as shown in(g). Throughout this study, the polarization direction of the incident ultra-short pulses is along the dimer axis (or y-axis) and the ultrafast laser pulse is incident on the entire space.

3. Results and discussion

3.1. Effect of size-asymmetry on ultrafast plasmon dynamics

In this section we will introduce size-asymmetries into homodimer by keeping the diameter of the first nanodisk(ND1)constant while varying the geometry of the second nanodisk(ND2)(see Figs.1(b)–1(e)).Figure 2 shows the ultrafast plasmon responses of constantly morphed symmetric Au ND dimer into size-asymmetric dimer by increasing the diameter of ND2 from 100 nm to 160 nm. The spectral intensity of near-fields shows only one dominant peak(mode I)and strong near-field intensity (about 260 a.u.) at 707 nm for Au ND homodimer(see Fig.2(a)black curve). This is due to the fundamental mode of the dimer system, which is known as the bonding dipole-dipole mode.[26]The hybridization of dipolar resonance in each ND creates a“hot spot”where the electromagnetic field in the dimer junction is greatly enhanced.[25]The size of ND2 increases to 160 nm, the intensity of the main plasmonic peak decreased from 261 a.u. to 139 a.u.(see Fig. 2(a) olive curve). This is due to the size-mismatch in asymmetric dimers and leads to a weakening of the coupling strength.[27]This interpretation is supported by the corresponding spatial and surface charge distribution of electric near fields (see Figs. 2(b2) and 2(c2), respectively). The resonant wavelength of this dipole–dipole mode is linked to the size of ND2, which shifts to a longer wavelength by increasing its size from 100 nm to 160 nm.[28]Moreover,the effect of symmetry breaking leads to the splitting of a single peak into three peaks of the resonance modes at around 739 nm,593 nm,and 560 nm. The spectral intensity of this asymmetric dimer has a narrower linewidth than the symmetric dimer and thus corresponds to a longer time signature. This can be further supported by the ultrafast dynamics of size-asymmetric dimers(see in Fig.2(d)). Generally,the spectral intensity shows drastic changes, shifting to a longer wavelength and additional peaks as the symmetry of the nanodimer is broken by increasing the size of one disk. These results indicate that the effect of symmetry breaking on symmetric Au ND dimer results in significant changes in the ultrafast plasmon responses.[29]

To further support our quantitative results,we calculated the spatial and charge distribution properties of near fields of symmetric Au ND dimers with ND 100 nm–100 nm and size-asymmetric Au ND dimers with ND 100 nm–160 nm at mode I and mode III,as presented in Figs.2(b)and 2(c). The strongest electric field distribution intensity is concentrated in the gap region and the edges of NDs of mode I at 707 nm for the symmetric dimer case as shown in Fig.2(b3). This is owing to the spectral intensity that is mainly contributed by both NDs. The surface charge distribution has the opposite signs,and this observation confirms the dipole–dipole interaction of hybridized coupling modes between the two nanodisks(see Fig. 2(c3)). Similarly, local electric field enhancement of mode I at 739 nm is mainly concentrated in the mid-gap region for size-asymmetric dimer and exhibits weak field intensity due to the size-mismatch as shown in Fig.2(b2). The surface charge distribution has the reverse charges in between size-asymmetric nanodisks (see Fig. 2(c2)). It is shown in Fig.2(b1)the spatial distribution of the near-fields of mode-III concentrated in the mid-gap region and around ND1 as well as it becomes weak at the ND2 side. Furthermore, the surface charge distribution of this mode revealed a dipole-quadrupole plasmon mode(see Fig.2(c1)). As it was reported in our previous work,[16]mode III shows that Fano resonance results from the interference of dipole mode of ND1 with the diameter of 100 nm and quadrupole mode of ND2 with the diameter of 160 nm.[30,31]It is well-known that the size-asymmetric Au ND dimer exhibits dipole–dipole mode at the resonant peak of 739 nm and dipole–quadrupole mode resonance at 560 nm.Hence,as it can be seen from Figs.2(b)and 2(c),varying the size of ND2 in symmetric Au ND dimer has a considerable effect on the spatial and charge distribution properties of near fields.

To gain a direct understanding of the effect of symmetry breaking on the ultrafast plasmon dynamics,we computed the evolution of temporal profiles of symmetric Au ND dimer by varying the size of ND2 from 100 nm to 160 nm for a fixed geometry of ND1 with 100 nm as shown in Fig.2(d). Theycomponent of the electric field amplitudes is selected since this component is directly excited by the polarized ultra-short laser pulse[15]so that the associatedxandzcomponents of these systems are too weak and negligible. This component of the electric field amplitudes is significantly affected by the variation of the size of ND2. The temporal profile of symmetric Au ND dimer in Fig. 2(d) black curve clearly shows a single temporal maximum in the amplitude, whose oscillation time starts from 20 fs to 60 fs, and no mode beating. The oscillation of this temporal maximum comes simply from the excitation pulse. Moreover,this symmetric dimer shows the highest frequency in its temporal profile of near-field oscillations.[32]Thus, our results clearly show that the ultrafast temporal dynamics can be controlled in symmetric Au ND dimer by varying the diameter of ND2.

Fig.2. The effect of size-asymmetry on near field intensities in the Au nanodisk dimer. (a)Spectral intensities of gap plasmons as a function of the different sizes of ND2 while a fixed geometry of ND1 in symmetric Au ND dimer. [(b),(c)]Spatial variations of the local electric field and surface charge distribution profiles of the symmetric dimer with ND 100 nm–100 nm and size-asymmetric dimer with ND 100 nm–160 nm associated with the three resonances,respectively. (d)Ultrafast plasmon dynamics of the electric near fields of the dominant component of Au nanodisk dimer by varying the geometry of the first nanodisk exited by a single ultra-short pulse. The incident light in the simulations was linearly polarized along the dimer axis(y-axis).

It is possible to increase the size of ND2 from 100 nm to 160 nm, however, the single temporal maximum gradually splits into three maximum oscillations. Therefore, the effect of broken symmetry affects the excitation of different LSPR modes and it can significantly adjust the ultrafast dynamics of the local fields,[33]which corresponds to an electric field oscillation time from 20 fs to 90 fs. Unlike the symmetric dimer,the ultrafast dynamics of size-asymmetric dimers show decreased amplitude and additional oscillations as the size of ND2 increases(see in Fig.2(d)from bottom to top). Temporal dynamics of size-asymmetric dimers under a single pulsed excitation show the three temporal maximum and prolonged times as well as showing up to two mode-beatings. Moreover,these dimers show the lowest frequency in the temporal profile of near-field oscillations,which has a striking difference compared to the symmetric dimer (see in Fig. 2(d) olive curve).Due to the energy transfer between unequal NPs, the temporal oscillation of size-asymmetric dimers oscillates for much longer than the symmetric one. For timest ≥55 fs the ultrafast temporal dynamics of this heterodimer shows a clear signature of mode beatings. We understand that the asymmetric excitation leads to the observation of these mode beatings.[6]The differences in the temporal dynamics of size-asymmetric dimers arise from a combination of broken symmetry and the coherent superposition between different modes.

3.2. Coherent control of ultrafast plasmon dynamics

In this section,we have performed the effect of the phase and time delays of symmetric and size-asymmetric dimers on ultrafast plasmon responses.For extremely small temporal delays among the ultra-short pulses,controlling the ultrafast responses of these systems by varying the phase delay of the excitation pulses is vital to ultrafast temporal regimes.[13,34]Initially, we studied the ultrafast responses of gap plasmons in symmetric and size-asymmetric dimers by controlling the phase delay between two identical driving pulses each having 15 fs pulse duration (the time delaytDis set to 0 fs between the two laser pulses),as presented in Fig.3. The resultant intensities of local electric fields of both systems with different relative phases and a fixed time delay between the pulses can be seen in Figs. 3(a) and 3(b), respectively. Their near-field intensity has to be understood as a resultant intensity which is based on the coherent superposition of identical,but phasedelayed near-fields induced by the first and second ultra-short pulses.

When the ultra-short pulses have the same phase (Δφ=0), the resultant intensity (IR) of Au ND homodimer exhibits a single resonance mode and maximum intensity ofIR=520 a.u. (see Fig. 3(a) black curve). This is due to the constructive interference of the resulting near fields. Moreover,for symmetric Au ND dimer,the resultant intensity tends to exhibit a broad spectrum, which causes shorter plasmonic field decay. As the phase delay between the pulses is varied from Δφ=0-π,the resultant electric near-field intensity decreases fromIR=520 a.u.to 133 a.u. This can be attributed to the delayed coherent couplings of the local electric fields at the inter-particle gap region.[14]This drastic decline of the resulting intensity with the relative phase delay can be explained by plasmon retardation resulting from the weak coupling between local fields induced by ultra-short pulses with different phases as shown in Fig.3(a)olive curve.[6,35]The results clearly show that the resultant near field intensity of local fields can be controlled at the mid-gap region of the symmetric system by varying the relative phase between the ultra-short pulses.

Fig. 3. Resultant intensities of (a) symmetric and (b) size-asymmetric Au nanodisk dimers exited by two parallel ultrafast laser pulses having similar pulse duration(τ =15 fs and the time delay tD between the two laser pulses is set to 0 fs)and same central wavelength(λ =718 nm)but with different relative phases. The direction of polarization of the incident pulses along the dimer axis of both systems.

Similarly,when the ultra-short pulses have similar phase(Δφ=0), the resultant intensity (IR) of the size-asymmetric dimer shows three peak intensities of 148 a.u. at mode III,176 a.u. at mode II, and 279 a.u. at mode I, respectively, as shown in Fig. 3(b) black curve. Compared to the symmetric dimer,this asymmetric dimer shows new electric near-field intensity peaks,which result from broken symmetry.[34]The resultant intensity decreases from 148 a.u.to 39 a.u.,176 a.u.to 48 a.u.and 279 a.u.to 72 a.u.,respectively as the phase delay increases from 0 toπ(see Fig. 3(b) black and olive curves).This radical drop of the resultant intensity with phase delay shown in Fig. 3(b) can be understood by the combination of plasmon retardation due to phase variations of the excitation field across the dimer, in cooperation with the coherent superposition of different LSPR modes resulting from the effect of symmetry breaking.[6,35]Furthermore, using two identical pulses with zero phase delay(Δφ=0),we confirmed that the resultant intensity of the local fields is higher in the symmetric dimer compared to the size-asymmetric dimer.

Let us now explore ultrafast dynamics of symmetric Au ND and size-asymmetric Au ND dimers with different relative phases for a fixed time delay between pulses. It is evident from Figs.4(a)and 4(b)that the amplitude of electric fields of symmetric dimer is significantly affected by the variation of the phase delays between the pulses.The amplitude(Ey)of the symmetric dimer shows a single dominant temporal maximum with a magnitude of 12.6 V/m and no beats(see Fig.4(a)red curve). Moreover,this temporal maximum leads to the shorttime coherent energy dissipation within the symmetric Au ND dimer.[36]The oscillation of this single temporal maximum retains some features of the excitation pulses and thus it dominates the associatedxandz-components.[13,37]Besides, the relative phase delay among the pulses increases from 0 toπ,the amplitude of the corresponding ultrafast dynamics declines from 12.6 V/m to 2.8 V/m(see Fig.4(a)red and Fig.4(b)olive curves). Moreover, the intensity of ultrafast dynamics of the gap plasmon shows similar features of the resultant near-field intensity shown in Fig. 3(a). The control of the phase delay between the pulses could be used for manipulation of ultrafast plasmon dynamics of the local fields in the symmetric dimer.

The ultrafast dynamics of the size-asymmetric Au ND dimer upon excitation of double pulses shows an interesting response and it can be greatly influenced by the relative phases of the pulses. For the size-asymmetric Au ND dimer along the dimer axis with Δφ= 0 the amplitude of ultrafast dynamics dominates three temporal maximum oscillations with two beats and extended time as shown in Fig.4(c)red curve.These temporal oscillations in this asymmetric dimer disclose the mode beating that results from the combination of broken symmetry and a coherent superposition of multiple localized surface plasmon modes induced by broad bandwidth of the ultrafast laser pulses.[38]Furthermore, the temporal profiles with the number of oscillations and mode beatings are indeed the significant features of the ultrafast dynamics in asymmetric dimers.[36]On the other hand, as one increases the phase delay among the ultra-short pulses from 0 toπ,the amplitude of ultrafast dynamics of size-asymmetric dimer shows reduced amplitude(as shown red curve in Fig.4(c)and olive curve in Fig. 4(d)). Moreover, the intensity of ultrafast dynamics of the gap plasmon shows comparable features of the resulting near-field intensity shown in Fig.3(b).

Fig. 4. Ultrafast plasmon dynamics of (a) symmetric and (c) size-asymmetry of Au nanodisk dimers exited by two ultrafast pulses with a relative phase difference of (Δφ =0). While (b) symmetric and (d) size-asymmetric dimers, respectively depict the electric field amplitudes of local fields exited by the pulses with phase delay varied from π/4 to π. The direction of polarization of the incident pulses along the dimer axis of both systems.

The spectral intensities and ultrafast dynamics of symmetric Au ND and size-asymmetric Au ND dimers were calculated as a function of the time delay between two ultra-short laser pulses. Figures 5(a) and 5(b) depict the spectrum and Figs.5(c)and 5(d)show the ultrafast dynamics of symmetric dimer and size-asymmetric dimers,respectively under doublepulsed excitation along the same direction for the different time delays. As it can be seen from Fig.5(a)black curve,the results of the symmetric dimer exited by two identical ultrashort pulses with zero time delay (tD=0 fs) reveals that the resultant electric near-field intensity shows a maximum intensity of aboutIR=520 a.u. This can be elucidated by the constructive interference of the composing pulses. The resultant near-field intensity of symmetric dimer is affected by the time delay between the pulses.

The resultant intensity of the gap plasmon tends to decrease in magnitude as the temporal delay increases from 0 fs to 60 fs. Thus, the spectral intensity of the symmetric dimer reveals several peaks,which are ascribed to the destructive interference of the local fields. At 20 fs,we observed six spectral peaks in the near field intensity while one central peak and the different spectral peaks can be observed at the short and long wavelength sides for 40 fs. We further increased the time delay to 60 fs, the number of peaks increases significantly as shown in Fig. 5(a) magenta curve. Moreover, the line width of peaks of the symmetric dimer is broader,indicating a faster decay of the near fields in the mid-gap region. Our results are further supported by the ultrafast dynamics(see Fig.5(c)).Furthermore, the spectral interference among temporally delayed pulses induces the significant spectral variation in the resultant intensity of symmetric dimer. Hence, the resultant intensities of local electric fields show a strong disparity for different values of offset times.

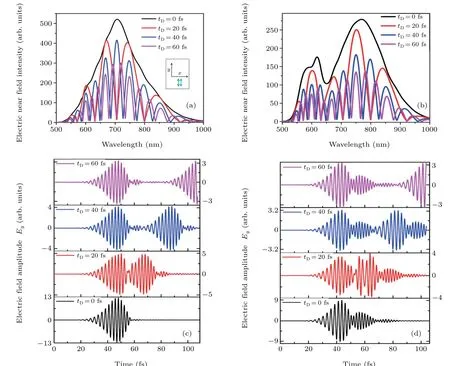
Fig. 5. Resultant intensities and ultrafast temporal profiles exited by parallel ultrafast pulses each having similar pulse duration (τ =15 fs) and the same relative phase(Δφ =0)but with different offset times. The resultant intensities of gap plasmons of symmetric Au nanodisk dimer(a)and size-asymmetric Au nanodisk dimer(b)as a function of time delays. [(c),(d)]The effect of temporal delay(tD)on the ultrafast temporal profiles of local field intensities of gap plasmons of the two dimers as a function of offset times,respectively.

The size-asymmetric Au ND dimer is excited by two identical laser pulses with zero time delay(tD=0 fs),the resulting intensity displays three peaks of aboutIR=148 a.u.at mode III,IR=176 a.u.at mode II andIR=279 a.u.at mode I,respectively,as shown in Fig.5(b)black curve,which result from the effect of symmetry breaking. The resultant intensity tends to decrease in magnitude as the time delay between the pulses is changed from 0 fs to 60 fs(see in Fig.5(b)black and magenta curves). Due to the effect of symmetry breaking,the spectral interference between temporally delayed ultra-short incident pulses induces a significant spectral modulation of the resultant near-field intensity in the size-asymmetric Au ND dimer. Furthermore, the resultant near-field intensity of the main peak of this asymmetric dimer is red-shifted compared to the symmetric dimer.This is owing to the amplitude of temporal profile oscillates with a lower frequency than the amplitude of temporal profiles of the symmetric system. The line width of the peaks of the size-asymmetric Au ND dimer is narrower,indicating a slow decay of the near field in the mid-gap region. These facts are further supported by ultrafast temporal dynamics(see Fig.5(d)). Lastly,we study the ultrafast temporal responses of both symmetric and size-asymmetric systems for various offset times.

To investigate the time evolution of local fields in the symmetric Au ND dimer, we have calculated temporal profiles of near-fields by varying the time delay and a fixed phase delay among the laser pulses. The amplitude of the temporal response of the electric fields of Au ND homodimer is considerably affected by the variation of the time delay between the pulses (see Fig. 5(c) in vertical scales). For a given symmetric dimer,we attained the highest amplitude ofEy=12.6 V/m and show a single dominant temporal maximum with no beats at zero temporal delay (see in Fig. 5(c) bottom black curve).Moreover, the amplitude of temporal profiles displays only a single temporal maximum and leads to the short-time coherent energy dissipation within the symmetric Au ND dimer.The temporal delay among the pulses is increased from 0 fs to 60 fs,the amplitude ofEydecreases from 12.6 V/m to 3.3 V/m(see the vertical scales of Fig. 5(c) from bottom to top). The aforementioned decline of the amplitude of the local field with the time delays shown in Fig. 5(c) can be explained by plasmon retardation resulting from the weak coupling between local fields induced by the incident laser pulses.[6]Moreover,the ultrafast dynamics develop extra one temporal maximum oscillation with one beat at later times as one increases the time delay between two pulses,indicating the presence of spectrally narrow features in the spectral response.As it can be seen from Fig. 5(c) blue and magenta curves, introducing a time delay between the two pulses allows one to observe temporally delayed ultrafast evolution of the local fields.

In the same manner, to control the ultrafast plasmon dynamics of the size-asymmetric Au ND dimer, we calculated the temporal profiles of electric fields with different time delays between the pulses. As it can be seen from Fig. 5(d)bottom black curve, for size-asymmetric Au ND dimer alongy-component we attained the maximum amplitude of the local fieldEy= 8.5 V/m and the amplitude of electric nearfield dominates three temporal maximum oscillations with two beats and extended time at zero-time delay. The ultrafast temporal dynamics of the electric fields in the size-asymmetric Au ND dimer shows the number of oscillations and beats,which are indeed the significant features of this system. Compared to symmetrical dimer, this maximum temporal profile tends to decreases in magnitude,which is ascribed to the sizemismatch in the asymmetric dimer,in cooperation with the coherent superposition of different LSPR modes.[6,27,35]Due to the narrower linewidth and red-shifted spectral peaks,the decay time of ultrafast dynamics of the local field is longer and oscillates with a high frequency, respectively. On the other hand,as one increases the time delay between the pulses from 0 fs to 60 fs,the maximum amplitude of ultrafast dynamics of the local fields decreases in magnitude(see the vertical scales of Fig. 5(d) from bottom to top). We revealed that the ultrafast dynamics of size-asymmetric dimers strongly depend on the time delay of the pulses. More interestingly, the shape of the temporal response is significantly deformed due to the excitation of local plasmon modes with different frequency components. As it can be seen from Fig. 5(d) blue and magenta curves,introducing a time delay between the two ultrafast pulses which allows one to observe temporally delayed ultrafast response of the local fields and it has a significant effect on the ultrafast dynamics.[39]

Note that the simulated temporal dynamics of the nano system in this paper can reveal several important characteristics of the nano system that cannot be disclosed from the traditional spectral response of the system. For instance, (i) the temporal dynamics of the nano system can tell temporal maximum of the local field evolution and mode beating occurrence in the nano system;(ii)the response of the local electric field oscillation delays to the excitation laser pulse;[15](iii)temporal dynamics of the nano system offers rich information of the plasmon mode coupling of the designed system.

4. Conclusion

The effect of symmetry breaking is crucial to understanding the ultrafast plasmon responses of various plasmonics systems through geometry and morphology. Here,we have theoretically studied how the ultrafast plasmon dynamics depends on the broken symmetry in the Au ND dimer by changing the diameter of one nanodisk in the dimer whereas for a fixed geometry of the other nanodisk excited by a single femtosecond pulse.It has been found that the ultrafast temporal dynamics of size-asymmetric dimer show mode beatings. The symmetric dimer shows one broad spectral peak in the spectral intensity and short decay times in their ultrafast response,whereas sizeasymmetric dimer shows three spectral peaks and prolonged decay times. The size-asymmetric dimer may have three temporal maxima oscillations and two beats, whereas the symmetric system may have at most one temporal maximum in amplitude and no beat. The major difference between the ultrafast temporal responses of the two systems is the number of temporal oscillations and mode beats. The coherent control of the ultrafast plasmon responses of the symmetric Au ND and the size-asymmetric Au ND dimers is studied as a function of the time delay and relative phase difference of the excitation pulses. We numerically demonstrated that coherent control of the ultrafast plasmon dynamics of both dimers strongly depends on the phase and time delays of the pulses.As such, we expect that our results would be interesting and would open new paths to understanding the effect of symmetry breaking on the ultrafast plasmon responses of the symmetric NP dimers, as well as motivating further research within the ultrafast temporal responses of asymmetric dimers. However,this work did not consider the effect of the substrate on the temporal characteristics of our designed systems,thus we recommend further study on such effects.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant Nos.91850109 and 61775021),“111”Project of China(Grant No.D17017),Key Laboratory of Ultrafast and Extreme Ultraviolet Optics of Jilin Province, and Ministry of Education Key Laboratory for Cross-Scale Micro and Nano Manufacturing, Changchun University of Science and Technology.