Influence of optical nonlinearity on combining efficiency in ultrashort pulse fiber laser coherent combining system

Yun-Chen Zhu(朱云晨) Ping-Xue Li(李平雪) Chuan-Fei Yao(姚传飞) Chun-Yong Li(李春勇)Wen-Hao Xiong(熊文豪) and Shun Li(李舜)

1Institute of Ultrashort Pulsed Laser and Application,Faculty of Materials and Manufacturing,Beijing University of Technology,Beijing 100124,China

2Department of Physics,Durham University,South Road,Durham DH1 3LE,UK

Keywords: coherent beam combination,spectral coherence,optical nonlinearity

1. Introduction

High-power ultrashort pulse fiber laser source features excellent beam-quality and structure-robustness, leading to its wide application in industrial and scientific territories.[1–3]However, due to the thermal effect caused by high average power and the nonlinear effect caused by high peak power,the output of a single fiber laser amplifier is limited.[4–6]To break this limitation, the coherent beam combination (CBC)technique[7]has been successfully applied,and great progress has been made.[8–13]In the CBC system,ultrashort pulse laser is firstly divided into multiple sub-beams that are launched into individual fiber amplifiers for power enhancement, and then these amplified sub-beams are coherently combined to obtain a new laser beam. The combining efficiency,which is defined as the ratio of the combined power to the summation power of the sub-beams, is the key indicator to assess the CBC performance. Physically,the combining efficiency reflects the optical coherence between the sub-beams.In short,achieving high combining efficiency essentially requires that the sub-beams are coherent in all temporal, spatial and spectral domains.However, it is unavoidable to accumulate optical-field mismatch between the sub-beams during their individual amplification and transmission process, which results in an optical coherence decay between them and causes the combining efficiency to decrease.[14–16]For the CBC of ultrashort pulse fiber laser,the temporal and spatial factors affecting the combining efficiency are similar to those in the CBC of continuous-wave(CW) laser, which had been studied in detail earlier.[17–21]However, different from the CW case, the ultrashort pulse fiber laser is also affected by optical nonlinearity caused by the self-phase modulation(SPM),[22–24]which usually causes the transformation in spectral intensity-phase distribution.[25,26]Therefore,the sub-beams going through different optical nonlinearity accumulation will show different spectral distributions, which weakens the spectral coherence between them and leads to the loss of the combining efficiency. At present,there are just a few studies on the influence of optical nonlinearity on the combining efficiency, in which only the spectral phase mismatch was theoretically analyzed,[14,27]while the spectral intensity mismatch has not been considered. In fact, the combining efficiency is influenced by both the spectral intensity and phase mismatch.

In this paper, we extended the research on the spectral coherence between ultrashort pulsed fiber laser beams from the exclusive spectral phase analysis to a comprehensive spectral intensity-phase analysis. The influence of optical nonlinearity on the combining efficiency is investigated theoretically and experimentally. In the theoretical work,by establishing a new theoretical algorithm, the coherent combining efficiency is accurately analyzed by numerically solving the nonlinear Schr¨odinger equation(NLSE)to obtain the spectral intensityphase information. In the experimental work,by establishing a CBC system involving two all-fiber picosecond laser subbeams, the degradation of combining efficiency originating from the imbalanced optical nonlinearity is studied. The experimental study agrees with the theoretical prediction. The results of this paper explain the influence of optical nonlinearity on the combining efficiency,which is helpful for the CBC of ultrashort pulse fiber lasers.

2. Theoretical algorithm

For the ultrashort pulse fiber laser, the most typical CBC scheme is the coherent polarization beam combination(CPBC),[28–30]to which we will pay our attention in the next theoretical and experimental work, nevertheless the results in this paper can also be applied to other combination schemes.The schematic diagram of the basic combining unit and array extension structure of the CPBC system are shown in Figs. 1(a) and 1(b), respectively. As shown in Fig. 1(a), two linearly polarized collimated beams(P1andP2),generated by the same oscillator and amplified by the individual amplifiers(omitted in Fig.1),pass through half-wave plates(HWP1 and HWP2),then enter a polarized beam combiner(PBC1). When the HWPs adjust their polarizations relative to the PBC1 to be p-polarized and s-polarized, respectively, the laser beams will come out from the same port of the PBC1. If there is no mismatch between the two sub-beams in any aspect of the temporal, spatial and spectral domains, and the temporalphase difference between them is locked to benπby using the phase control technique,[31,32]wherenis an integer, the two sub-beams will be combined into a new linearly polarized beam. The combined beam then enters PBC2 after the polarization adjustment by HWP3,and the output beam transmitted or reflected from PBC2 can be used in the next-stage combination. The array extension structure of the CPBC system,as shown in Fig.1(b),is in fact the cascaded reproduction of the above CPBC unit, so the analysis of the CPBC unit is fundamental.[33,34]

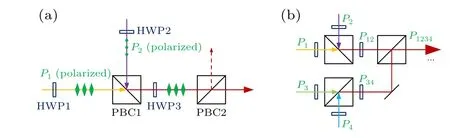
Fig.1. The schematic diagram of(a)the basic combining unit,and(b)array extension structure of the CPBC system.

It is well known that the effect from SPM quantified by the parameter ofB-integral that indicates the accumulated maximum phase-shift for the laser pulse and originates from the change of laser intensity in the temporal domain, will alter the spectral dimensionality of the laser. Therefore, it is necessary to accurately acquire the spectral information of the sub-beams to quantitatively analyze the impact of optical nonlinearity imbalance on the combining efficiency in the CPBC system. In the previous studies, analytic expression[14,27]for the combining efficiency had been obtained by ignoring the spectral intensity mismatch between the sub-beams. It was successfully applied to the ultrashort pulse laser systems operated in the linear region where theB-integral is less thanπrad(the dimension“rad”for theB-integral will be omitted below for the simplification), but it cannot be applied to those systems operated in the nonlinear region where theB-integral is greater thanπ,in which both the spectral intensity and phase are strongly changed. Different from the previous studies, in this paper a new theoretical algorithm is adopted to accurately predict the combining efficiency enabling a wider applicability of the result. This theoretical algorithm uses the spectral information arriving from the numerical result of the NLSE,and then the accurate prediction of the combining efficiency can be obtained. Here,it is assumed that the CPBC case involves two ultrashort pulse fiber lasers with the same power but differentB-integral accumulation,and the algorithm is presented in detail below:

Step 1 Initialize the necessary information for the laser pulses and fiber amplifiers.

Step 2 Numerically solve the NLSE based on the splitstep Fourier method[35]that had been known for the community to obtain the temporal information of the sub-beams.

Step 3 Get the spectral information by taking the Fourier transform of the temporal information in Step 2,and then the spectral intensity and phase distribution of the laser pulse are obtained.

Step 4 Substitute the spectral intensity and phase distribution into the theoretical model of the CPBC[36]for numerical calculation.

Step 5 Obtain the theoretical prediction of the combining efficiency,and then the algorithm is finished.

In the simulation of the above theoretical algorithm,it is assumed that the fiber parameters of the two parallel amplifiers are the same,while the gain coefficients of them are different,which results in differentB-integral accumulation (however,their amplified power values are scaled to the same to eliminate the power imbalance effect on the calculation result). It is also assumed that the two sub-beams align perfectly both in temporal and spatial domains to eliminate the cross effect on the calculation result. Then, the combining efficiency of the two sub-beams suffering imbalancedB-integral accumulation is shown in Fig. 2. The horizontal axis in the figure represents the ratio of theB-integrals of the two sub-beams(B2/B1), and the vertical axis represents the prediction of the combining efficiency. The five curves in the figure represent the simulation results corresponding to theB-integral of the first sub-beam (B1) being 0.40π, 0.59π, 1.02π, 1.51π, and 2.47π, respectively. It shows that the combining efficiency decreases with the increase ofB2/B1. Moreover, the greater theB1, the more sensitive the combining efficiency is to theB2/B1. The above results indicate that it is necessary to carefully manage theB-integral accumulation of the sub-beam to ensure a great combination.Besides,the calculated points corresponding toB2-B1=0.35πon these curves are marked in blue. It is interesting to note that except for the marked point on the fourth curve,the other points almost correspond to the same combining efficiency value. To understand the physical mechanism about these results in Fig.2,an additional analysis is conducted below.

Fig. 2. Dependence of the combining efficiency on B2/B1, with B1 being 0.40π,0.59π,1.02π,1.51π,and 2.47π respectively.

From the physical viewpoint, along with the increase ofB-integral, the bandwidth is broadened and the multi-peak structure will occur to the spectral intensity distribution, and meanwhile the transformation from linear to nonlinear chirp will occur to the spectral phase distribution. To clarify the influence of the spectral intensity and phase mismatch separately,the above five combining efficiency curves are recalculated,but the two physical mechanisms,i.e.,the spectral intensity mismatch and spectral phase mismatch,are considered independently. The corresponding calculation results are shown in Figs. 3(a)–3(e). In these figures, the red solid lines represent the combining efficiency evolution when there are mismatches both in the spectral intensity and phase distributions(consistent with the five curves in Fig.2), while the blue and yellow dashed lines represent the predicted cases when there is mismatch only in the spectral intensity or phase distributions,respectively. From these results,it shows that when the system runs within the linear region,the blue dashed lines decrease more significantly than the yellow ones, which shows the main factor leading to the degradation of spectral coherence between sub-beams is the spectral intensity mismatch.However, when the system runs within the nonlinear region,the main factor leading to the degradation of spectral coherence between sub-beams reverses to the spectral phase mismatch. These results indicate that, in the linear region, the spectral phase reshaping shows as approximately linear chirp,which can be effectively compensated by the phase-locking process in the system (the phase-locking had been included in the simulation process), so the influence of spectral phase mismatch is weak. However, in the nonlinear system, the spectral phase reshaping shows as nonlinear chirp that cannot be fully compensated, so the influence of spectral phase mismatch plays a major role.

Fig.3. Dependence of the combining efficiency on B2/B1,with B1 being(a)0.40π,(b)0.59π,(c)1.02π,(d)1.51π,and(e)2.47π respectively,considering the mismatch only in spectral intensity(blue dash line)or phase(yellow dash line)distribution,as well as both of them(red solid line).

Based on the results in Fig. 3, some important features in Fig. 2 can be additionally interpreted. Firstly, asB1increases, the system gradually transfers from linear to nonlinear region, which results in the different evolution trend for the five curves. Secondly, the marked points correspondingB2-B1=0.35πon the first, second and third curves represent near-linear chirp mismatch, which had been already effectively compensated,thus giving them similar combining efficiency values. However, for the marked point on the fourth curve,a significant nonlinear chirp mismatch occurs,resulting in a significant decrease in the combining efficiency. For the marked point on the fifth curve,the situation is more complex,although at this case the nonlinear chirp mismatch is stronger,the combining efficiency right meets a smooth window, and finally it still obtains a high value. However, considering the difficulty of chirp management,it is not recommended to make a system operate in this state.

Furthermore,as an effective application of the theoretical algorithm presented above, the combining efficiency calculation for the multi-channel ultrashort pulse fiber laser CPBC system,which suffers imbalanced optical nonlinearity,will be provided below. Here, it is assumed that the combining case is a CPBC system consisting of four equal-power sub-beams(P1,P2,P3,P4)as shown in Fig.1(b),while theirB-integrals areB1=0.50π,B2=1.02π,B3=1.51π,andB4=1.73π,respectively.The four-channel combining case here actually involves two-stage combination. In the first stage combination,P1andP2are combined intoP12featuring the combining efficiency ofη1, whileP3andP4are combined intoP34featuring the combining efficiency ofη2. In the second stage combination,P12andP34are additionally combined intoP1234featuring the combining efficiency ofη3. To obtain the overall combining efficiency ofη(η=η1η2η3) for this four-channel combining case,it is necessary to get the calculation results ofη1,η2andη3. Firstly,by using the theoretical algorithm established above,η1andη2can be directly calculated to be 95.34%and 86.32%,respectively. Then,to obtain the calculated result forη3by using the theoretical algorithm,one could substitute the specific information ofP12andP34as two new sub-beams into the algorithm. Here, by obtaining the information of the two new sub-beams based on the CPBC model[36]that had been known for the community,η3can be additionally calculated to be 84.83%. Finally, the overall combining efficiency ofηin this case can be calculated to be 69.81%. Therefore,as the example described above, the theoretical algorithm presented in this paper for the CPBC unit can also be successfully applied to the multi-channel laser coherent combining system.

3. Experimental results

In order to experimentally investigate the influence of optical nonlinearity on the combining efficiency, a CPBC system involving two ultrashort pulse fiber laser sub-beams is built, which is shown in Fig. 4. The front stage in the system is composed of a picosecond pulse single-mode (SM)polarization-maintaining (PM) fiber laser seed, a SM-PM fiber pre-amplifier and a SM-PM fiber stretcher. The seed source is based on the semiconductor saturable absorber mirror(SESAM)mode-locking,which can generate a linearly polarized slow-axis beam with repetition rate being 14.49 MHz,pulse width being 12.9 ps(the autocorrelation trace is shown in Fig.5(a)),central wavelength being 1064.2 nm,spectral coverage range being 1.1 nm(the spectrum intensity is shown in Fig. 5(b)), and average power being 3.63 mW. The average power of the seed laser is raised to 58 mW by using the fiber pre-amplifier, then the amplified laser beam enters the fiber stretcher made up of～500 m SM-PM fiber,in which the laser pulse is stretched in both temporal and spectral domains under the joint effect of group velocity dispersion(GVD)and SPM.The waveform trace and spectrum intensity of the laser beam emitted from the fiber stretcher are shown in Figs. 6(a) and 6(b), respectively. They show that the pulse width is 247 ps and the spectral coverage range is 18 nm. Note that,due to the strong optical nonlinearity accumulation, the spectral coverage range is scaled up to～16 times compared with that of the seed source,which indicates that the system is already running in a highly nonlinear region.

Fig.4. The diagram of the experimental CPBC system.

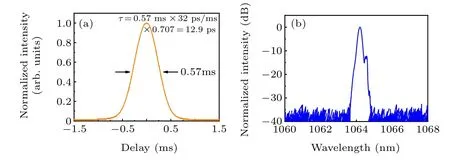
Fig.5.Measurement results of the output beam emitted from the seed source:(a)autocorrelation trace,(b)spectrum intensity.

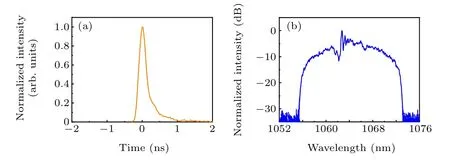
Fig. 6. Measurement results of the output beam emitted from the fiber stretcher: (a)waveform trace,(b)spectrum intensity.

Then, the laser beam emitted from the front stage is divided into two sub-beams by a fiberized PM beam splitter(FPBS) with the power splitting ratio of 7:3. Among them,the first sub-beam (the sub-beam emitted from the 70% output port of the FPBS), passes through an optical delay line(ODL) with a delay accuracy of 0.413 μm; while the second sub-beam(the sub-beam emitted from the 30%output port of the FPBS)passes through an electro-optical phase modulator(EOM), featuring a lower optical damage threshold than the ODL (which determines the imbalanced power splitting ratio for the FPBS), with a response bandwidth of 300 MHz. After that, the two sub-beams are launched into two individual cascaded PM fiber amplifier chains, respectively. Both fiber amplifier chains are made up of one SM-PM fiber amplifier and one 10/125 μm large-mode-area(LMA)PM fiber amplifier, in which the SM-PM ytterbium-doped fiber used in the first stage amplifier has an absorption coefficient of 250 dB/m at 976 nm spectral pump band and a length of～1 m,and the 10/125 μm PM ytterbium-doped fiber used in the second stage amplifier has an absorption coefficient of 4.95 dB/m at 976 nm spectral pump band and a length of～2.5 m.Note that the purpose of ODL and EOM embedded into the two sub-beams is to achieve optical-path and temporal-phase matching. In addition,the parameters of the optical devices in the two amplifier chains are also similar,to ensure a great match between them.

Next, the two independently amplified sub-beams enter a fiber polarization beam combiner (FPBC), which achieves the beam combining process without spatial mismatch. After that, the combined beam is collimated by using an aspherical lens and launched into free space. Here, the combined beam is divided into two laser beams by using the mirror M1 with reflectivity of 95%,and the weak transmitted beam from M1 is converted to electronic signal by using a photodetector (PD) with a response bandwidth of 150 MHz. Then the electronic signal is filtered by a low-pass filter(LPF)with an upper cutoff bandwidth of 240 kHz,to filter out the laser-seedbased repetition rate frequency spectrum component of MHz magnitude while preserve the temporal-phase noise that need to be corrected by the phase-locking controller next. Here,by executing the stochastic parallel gradient descent (SPGD)algorithm[31]using the digital signal processor (DSP) with a clock frequency of 150 MHz,the phase-locking signal is then generated at 25 kHz update rate and fed back to the EOM to achieve temporal-phase locking between the two sub-beams.On the other side of M1,the reflected beam is further divided into two parts by using the mirror M2 with transmissivity of 90%,and the transmitted beam from M2 is sent to a power meter to diagnose the combined power,while the reflected beam is sent to a polarized prism to diagnose the combining efficiency (the combining efficiency here is characterized as the ratio of the linear-polarized power to the total power of the combined beam).

According to the basic principle of the ultrashort pulse fiber laser amplifier,the higher the output power of the amplifier,the greater theB-integral accumulated for the laser pulse.In the experiment,the difference between optical nonlinearity accumulation of the two sub-beams is achieved by adjusting the gain of the main amplifier (i.e., the 10/125 μm PM fiber amplifier) in each channel, to generate the expected output power for each sub-beam (P1andP2). Firstly, when there is no pump laser launching into the main amplifiers, the output power of each sub-beam is set to be～30 mW,which is determined by the SM-PM fiber amplifier in each channel. Then,by gradually increasing the pump power of the main amplifiers, the gain of the main amplifiers can be controlled, and the output powers of the sub-beams can be thereby controlled.It should be noted that, in this experiment, the output power of each individual sub-beam is measured in turn at the common output-port of the FPBC, but without another sub-beam launching into the FPBC. During this process, by carefully calibrating the pump power values,the required output power values for each sub-beam,which would be inconvenient to be measured after the FPBC-based fiber loop is formed, is successfully converted to the corresponding pump power values of each main amplifier.

In the experiment for the combining efficiency investigation,ten different output power values,i.e.,50 mW,100 mW,150 mW,..., and 500 mW, are set in turn forP2, whileP1is set to be 1.5×P2during this process, to avoid the change of power-ratio which could simultaneously affect the measured combining efficiency. The measured combining efficiency result of these cases is shown in Fig. 7. The result shows that the combining efficiency decreases with the increase ofP2(along withP2increases,the value ofP1–P2increases),which indicates that the optical nonlinearity imbalance between the two sub-beams is gradually increased during the above process. In other words, along with this process, the mismatch of spectral intensity-phase distribution between the two subbeams increases gradually, therefore the spectral coherence between them decreases gradually, resulting in the reduction of the combining efficiency.

Fig.7. The measured combining efficiency dependent on the increase of P2(with P1=1.5×P2).

The above experimental result shows that the optical nonlinearity imbalance between the sub-beams will result in reduced combining efficiency. Conversely, it is conducted that the deteriorated combining efficiency may be improved by eliminating the optical nonlinearity imbalance between the sub-beams, which will be demonstrated in the next experiment. It has been indicated that, the optical nonlinearity accumulated in the first sub-beam is stronger than that of the second sub-beam during the above experiment, therefore, the difference between them should be decreased in the next experiment.Firstly,bothP1andP2are set to be 50 mW to ensure a similar optical nonlinearity for the two sub-beams,which results in a measured combining efficiency of 92.99%. Then,different from the experiment above,five different power values, i.e., 50 mW, 100 mW, 150 mW, 200 mW, and 250 mW are set in turn forP1,whileP2is set to be 1.5×P1during the process. The measured combining efficiency result of these cases is shown in Fig. 8. The result shows that with the increase ofP1, the combining efficiency firstly raises and then falls,reaching a maximum of 96.59%withP1=150 mW andP2=225 mW,which indicates that the optical nonlinearity imbalance between the two sub-beams is nearly disappeared at this case.The asymmetry ofP1andP2in this case should be attributed to the residual asymmetry for the two amplifier chains,in other words,although the final peak powers of the two subbeams are not the same in this case, they accumulate almost the same optical nonlinearity during their individual amplification and transmission process. Nevertheless,a small gap between the optimal combining efficiency of 96.59%obtained in the experiment and the theoretical maximum combining efficiency of 100%is still existing,which is mainly caused by the optical-path and temporal-phase control residual between the two sub-beams.Importantly,it should be noted that,by adjusting the amplifier gain of the sub-beam,the optical nonlinearity imbalance between the sub-beams has been successfully eliminated,resulting in an improved combining efficiency.

Fig.8. The measured combining efficiency dependent on the increase of P1(with P2=1.5×P1).

From a physical viewpoint, the combination of the two sub-beams described in the experiments is actually a statistical representation of the optical-field adding of each spectral longitudinal-mode involved in the sub-beams. Therefore,only when the spectral intensity and phase distributions of the two sub-beams are the same,these longitudinal-modes would simultaneously appear to be in the constructive-adding state,which leads to an ideal coherent addition state. Conversely,if there is mismatch in the spectral intensity or spectral phase distribution between the two sub-beams, only a part of these longitudinal-modes would appear to be in the constructiveadding state, while the other longitudinal-modes would appear to be in the weak constructive-adding or even destructiveadding state,which leads to a partially coherent addition state.In the ultrashort pulse fiber laser coherent combining system,if the individually amplified sub-beams accumulate differentB-integrals,their spectral intensity-phase distributions will become mismatched.Then,it will fail to combine the sub-beams with an ideal coherent addition state, thus reducing the combining efficiency.

The experimental results demonstrate the effect of imbalanced optical nonlinearity on the combining efficiency,which agrees with the theoretical analysis. At the same time, it should be noted that, different from the common coherent combining systems in which the ultrashort pulse lasers are usually operated in the linear region, the experimental system described in this paper is in a highly nonlinear region.Therefore,the coherent combination case suffering strong optical nonlinearity has been successfully verified in this paper,which provides a useful reference for the coherent combination of high-intensity ultrashort pulse laser in the future.

4. Conclusion

In this paper, the influence of optical nonlinearity on the combining efficiency in ultrashort pulse fiber laser coherent combining system is investigated theoretically and experimentally. In the theoretical work, it is found that the optical nonlinearity affects the spectral coherence between the sub-beams by changing their spectral intensity and phase distributions.When theB-integral is less thanπ, the main reason for the degradation of spectral coherence between the sub-beams is the spectral intensity mismatch,however,when theB-integral is greater thanπ,the main reason reverses to the spectral phase mismatch. In the experimental work, it is found that the optical nonlinearity imbalance weakens the spectral coherence between the sub-beams leading to a decrease of the combining efficiency,which is consistent with the theoretical expectation.By properly adjusting the gain of the laser amplifier, the optical nonlinearity can be adjusted to optimize the combining efficiency. In addition,the applicability of the CBC technique in ultrashort pulse laser system suffering strong optical nonlinearity is verified experimentally in this paper,which provides a useful reference for the future coherent combination of highintensity ultrashort pulse laser.

Acknowledgments

Project supported by the Key Program of Beijing Municipal Natural Science Foundation, China (Grant No. KZ201910005006), the National Natural Science Foundation of China(Grant No.62005004),Natural Science Foundation of Beijing Municipality, China (Grant No. 4204091),and National Science Foundation for Post-doctor Scientists of China(Grant No.212423).